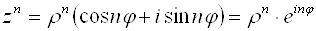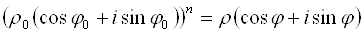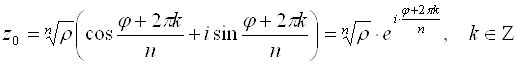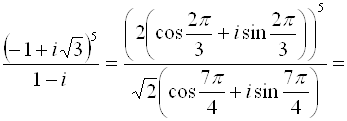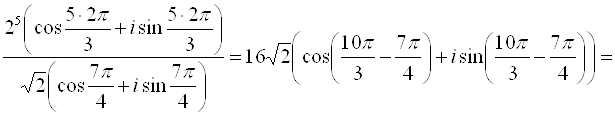Решение комплексных уравнений формула муавра

Второй урок по комплексным числам. Если вы только начинаете изучать эту тему (что такое комплексная единица, модуль, сопряжённые), см. первый урок: «Что такое комплексное число».

Сегодня мы узнаем:

Начнём с ключевого определения.

Видео:Формула Муавра ➜ Вычислить ➜ (5+5i)⁷Скачать

1. Тригонометрическая форма

Определение. Тригонометрическая форма комплексного числа — это выражение вида

[z=left| z right|cdot left( cos text!!varphi!!text+isin text!!varphi!!text right)]

где $left| z right|$ — модуль комплексного числа, $text!!varphi!!text$ — некоторый угол, который называется аргумент комплексного числа (пишут $text!!varphi!!text=arg left( z right)$).

Любое число $z=a+bi$, отличное от нуля, можно записать с тригонометрической форме. Для этого нужно вычислить модуль и аргумент. Например:

Записать в тригонометрической форме число $z=sqrt+i$.

Переписываем исходное число в виде $z=sqrt+1cdot i$ и считаем модуль:

Выносим модуль за скобки:

[z=sqrt+1cdot i=2cdot left( frac<sqrt>+fraccdot i right)]

Вспоминаем тригонометрию, 10-й класс:

Понятно, что вместо $frac<text!!pi!!text>$ с тем же успехом можно взять аргумент $frac<13text!!pi!!text>$. Синус и косинус не поменяется. Главное — выбрать такой аргумент, чтобы в тригонометрической форме не осталось никаких минусов. Все минусы должны уйти внутрь синуса и косинуса. Сравните:

Записать в тригонометрической форме число $z=-1-i$.

Видео:Формула Муавра. Возведение комплексного числа в степеньСкачать

2. Умножение и деление комплексных чисел

Комплексные числа, записанные в тригонометрической форме, очень удобно умножать и делить.

Теорема. Пусть даны два комплексных числа:

[begin & <_>=left| <_> right|cdot left( cos alpha +isin alpha right) \ & <_>=left| <_> right|cdot left( cos beta +isin beta right) \ end]

Тогда их произведение равно

[<_>cdot <_>=left| <_> right|cdot left| <_> right|cdot left( cos left( alpha +beta right)+isin left( alpha +beta right) right)]

А если ещё и $left| <_> right|ne 0$, то их частное равно

Получается, что при умножении комплексных чисел мы просто умножаем их модули, а аргументы складываем. При делении — делим модули и вычитаем аргументы. И всё!

Найти произведение и частное двух комплексных чисел:

[begin <_>cdot <_> & =2cdot 5cdot left( cos left( frac+frac right)+isin left( frac+frac right) right)= \ & =10cdot left( cos frac+isin frac right) \ end]

[begin frac<<_>><<_>> & =fraccdot left( cos left( frac-frac right)+isin left( frac-frac right) right)= \ & =0,4cdot left( cos frac+isin frac right) \ end]

По сравнению со стандартной (алгебраической) формой записи комплексных чисел экономия сил и времени налицо.:)

Видео:Комплексные числа. Тригонометрическая форма. Формула Муавра | Ботай со мной #040 | Борис Трушин !Скачать

3. Формула Муавра

Пусть дано комплексное число в тригонометрической форме:

[z=left| z right|cdot left( cos text!!varphi!!text+isin text!!varphi!!text right)]

Возведём его в квадрат, умножив на само себя:

[begin <^> & =zcdot z = \ & =left| z right|left| z right|cdot left( cos left( text!!varphi!!text!!varphi!!text right)+isin left( text!!varphi!!text!!varphi!!text right) right)= \ & =<^>cdot left( cos 2text!!varphi!!text+isin 2text!!varphi!!text right) \ end]

Затем возведём в куб, умножив на себя ещё раз:

Несложно догадаться, что будет дальше — при возведении в степень $n$. Это называется формула Муавра.

Формула Муавра. При возведении всякого комплексного числа

[z=left| z right|cdot left( cos varphi +isin varphi right)]

в степень $nin mathbb$ получим

Простая формула, которая ускоряет вычисления раз в десять! И кстати: эта формула работает при любом $nin mathbb$, а не только натуральном. Но об этом позже. Сейчас примеры:

Представим первое число в тригонометрической форме:

[begin sqrt-i & = 2cdot left( frac<sqrt>+icdot left( -frac right) right)= \ & =2cdot left( cos left( -frac right)+isin left( -frac right) right) \ end]

По формуле Муавра:

Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.

Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:

Теперь второе число запишем в комплексной форме:

По формуле Муавра:

Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.

Видео:Комплексные числа: начало. Высшая математика или школа?Скачать

4. Дополнение 1. Геометрический подход

Многие путают местами косинус и синус. Почему комплексная единица стоит именно у синуса? Вспомним, что есть декартова система координат, где точки задаются отступами по осям $x$ и $y$:

А есть полярная система координат, где точки задаются поворотом на угол $varphi $ и расстоянием до центра $r$:

А теперь объединим эти картинки и попробуем перейти из декартовой системы координат в полярную:

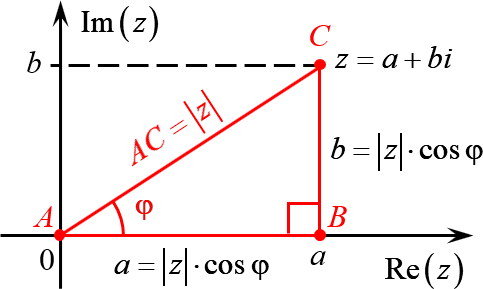
Комплексное число $z=a+bi$ задаёт на плоскости точку $C$, удалённую от начала координат на расстояние

Треугольник $ABC$ — прямоугольный. Пусть $angle BAC=varphi $. Тогда:

[begin & AB=ACcdot cos varphi =left| z right|cdot cos varphi \ & BC=ACcdot sin varphi =left| z right|cdot sin varphi \ end]

С другой стороны, длины катетов $AB$ и $BC$ — это те самые отступы $a$ и $b$, с помощью которых мы задаём комплексное число. Поэтому:

[begin a+bi & =left| z right|cos varphi +icdot left| z right|sin varphi = \ & =left| z right|left( cos varphi +isin varphi right) \ end]

Итак, мы перешли от пары $left( a;b right)$ к паре $left( left| z right|;varphi right)$, где $left| z right|$ — модуль комплексного числа, $varphi $ — его аргумент (проще говоря, угол поворота).

Важное замечание. А кто сказал, что такой угол $varphi $ существует? Возьмём число $z=a+bi$ и вынесем модуль за скобку:

Осталось подобрать такой угол $varphi $, чтобы выполнялось два равенства:

Такой угол обязательно найдётся, поскольку выполняется основное тригонометрическое тождество:

На практике основная трудность заключается именно в поиске подходящего аргумента.

Видео:Формула Муавра для комплексных чисел. Пример 1Скачать

5. Дополнение 2. Как найти аргумент?

В учебниках пишут много разной дичи, типа вот этой:

Формула правильная, но пользы от неё — ноль. Запомнить сложно, а применять и вовсе невозможно. Мы пойдём другим путём.

5.1. Точки на координатных осях

Для начала рассмотрим точки, лежащие осях координат.

Тут всё очевидно:

• На положительной полуоси абсцисс $varphi =0$ (фиолетовая точка $A$).
• На отрицательной — $varphi =pi $ (синяя точка $B$).
• На положительной полуоси ординат $varphi =frac$ (зелёная точка $B$).
• На отрицательной — $varphi =frac$ (красная точка $C$). Однако ничто не мешает рассмотреть $varphi =-frac$ — результат будет тем же самым.:)

5.2. Точки с арктангенсом

А если точки не лежат на осях, то в записи комплексного числа $a+bi$ числа $ane 0$ и $bne 0$. Рассмотрим вспомогательный угол

Очевидно, это острый угол:

Зная знаки чисел $a$ и $b$, мы немедленно определим координатную четверть, в которой располагается искомая точка. И нам останется лишь отложить вспомогательный угол $<_>$ от горизонтальной оси в эту четверть.

В правой полуплоскости мы откладываем от «нулевого» луча:

Точка $Aleft( 3;4 right)$ удалена от начала координат на расстояние 5:

[begin 3+4i & =5cdot left( cos varphi +isin varphi right) \ varphi & =operatornamefrac end]

Для точки $Bleft( 6;-6 right)$ арктангенс оказался табличным:

[6-6i=6sqrtcdot left( cos left( -frac right)+isin left( -frac right) right)]

В левой полуплоскости откладываем от луча, соответствующего углу $pi $:

Итого для точки $Cleft( -2;5 right)$ имеем:

[begin -2+5i & =sqrtcdot left( cos varphi +isin varphi right) \ varphi & =pi -operatornamefrac end]

И, наконец, для точки $Dleft( -5;-3 right)$:

[begin -5-3i & =sqrtcdot left( cos varphi +isin varphi right) \ varphi & =pi +operatornamefrac end]

Звучит просто, выглядит красиво, работает идеально! Но требует небольшой практики. Пробуйте, тренируйтесь и берите на вооружение.

А в следующем уроке мы научимся извлекать корни из комплексных чисел.:)

Видео:Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать

Теорема Муавра: доказательство и решенные упражнения

Теорема Муавра: доказательство и решенные упражнения — Наука

Видео:Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

Содержание:

В Теорема Муавра применяет фундаментальные процессы алгебры, такие как степени и извлечение корней в комплексных числах. Теорема была сформулирована известным французским математиком Абрахамом де Муавром (1730 г.), который связал комплексные числа с тригонометрией.

Авраам Муавр создал эту ассоциацию через выражения синуса и косинуса. Этот математик создал своего рода формулу, с помощью которой можно возвести комплексное число z в степень n, которая является положительным целым числом, большим или равным 1.

Видео:Тригонометрическая форма комплексного числаСкачать

Что такое теорема Муавра?

Теорема Муавра утверждает следующее:

Если у нас есть комплексное число в полярной форме z = r_Ɵ, где r — модуль комплексного числа z, а угол Ɵ называется амплитудой или аргументом любого комплексного числа с 0 ≤ Ɵ ≤ 2π, чтобы вычислить его n-ю степень, нет необходимости умножать его на себя n раз; то есть не обязательно изготавливать следующий продукт:

Напротив, теорема гласит, что, записывая z в его тригонометрической форме, для вычисления n-й степени мы действуем следующим образом:

Если z = r (cos Ɵ + i _* sin Ɵ), тогда z п = г п (соз п * Ɵ + я _* сэн п * Ɵ).

Например, если n = 2, то z 2 = г 2 [соз ​​2 (Ɵ) + я грех 2 (Ɵ)]. Если n = 3, то z 3 = z 2 _* z. В дальнейшем:

z 3 = г 2 [соз ​​2 (Ɵ) + я грех 2 (Ɵ)] _* г [соз 2 (Ɵ) + я грех 2 (Ɵ)] = г 3 [соз ​​3 (Ɵ) + я грех 3 (Ɵ)].

Таким образом, тригонометрические отношения синуса и косинуса могут быть получены для кратных углов, если известны тригонометрические отношения угла.

Таким же образом его можно использовать для поиска более точных и менее запутанных выражений для корня n-й степени комплексного числа z, так что z п = 1.

Для доказательства теоремы Муавра используется принцип математической индукции: если целое число «a» обладает свойством «P», и если для любого целого «n», большего, чем «a», обладающего свойством «P», Это означает, что n + 1 также имеет свойство «P», тогда все целые числа больше или равные «a» имеют свойство «P».

Видео:Извлечение корня из комплексного числа. Формула Муавра.Скачать

Демонстрация

Таким образом, доказательство теоремы проводится в следующие шаги:

Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Индуктивная база

Сначала проверяется на n = 1.

Поскольку z 1 = (r (cos Ɵ + i _* сен Ɵ)) 1 = г 1 (cos Ɵ + i _* сен Ɵ) 1 = г 1 [cos (1_* Ɵ) + я _* сен (1_* Ɵ)] следует, что при n = 1 теорема выполнена.

Видео:✓ Задача про комплексное число | Ботай со мной #101 | Борис ТрушинСкачать

Индуктивная гипотеза

Предполагается, что формула верна для некоторого положительного целого числа, то есть n = k.

z k = (r (cos Ɵ + i _* сен Ɵ)) k = г k (cos k Ɵ + i _* грех к Ɵ).

Видео:11 класс, 10 урок, Извлечение корней из комплексных чиселСкачать

Проверка

Доказано, что это верно для n = k + 1.

Поскольку z к + 1 = z k _* z, то z к + 1 = (r (cos Ɵ + i _* сен Ɵ)) к + 1 = г k (cos kƟ + i _* сен кƟ) _* г (соз Ɵ + я_* сенƟ).

Затем выражения умножаются:

На мгновение фактор r игнорируется к + 1 , а общий множитель i берется:

Как и я 2 = -1, подставляем в выражение и получаем:

Теперь заказаны действительная и мнимая части:

Чтобы упростить выражение, для косинуса и синуса применяются тригонометрические тождества суммы углов:

соз (А + В) = соз А _* cos B — грех A _* сен Б.

грех (А + В) = грех А _* cos B — cos A _* cos B.

В данном случае переменными являются углы Ɵ и kƟ. Применяя тригонометрические тождества, мы имеем:

cos kƟ _* cosƟ — сэн ко _* sinƟ = cos (kƟ + Ɵ)

сен ко _* cosƟ + cos kƟ _* грех = грех (кƟ + Ɵ)

Таким образом, выражение выглядит так:

z к + 1 = г к + 1 (cos (kƟ + Ɵ) + я _* грех (kƟ + Ɵ))

z к + 1 = г к + 1 (cos [(k +1) Ɵ] + я _* грех [(k +1) Ɵ]).

Таким образом, можно показать, что результат верен для n = k + 1. По принципу математической индукции делается вывод, что результат верен для всех положительных целых чисел; то есть n ≥ 1.

Видео:Возведение в степень и извлечение корня из комплексного числаСкачать

Отрицательное целое число

Теорема Муавра также применяется, когда n ≤ 0. Рассмотрим отрицательное целое число «n»; тогда «n» можно записать как «-m», то есть n = -m, где «m» — положительное целое число. Таким образом:

(cos Ɵ + i _* сен Ɵ) п = (cos Ɵ + i _* сен Ɵ) -м

Чтобы получить показатель степени «m» положительным образом, выражение записывается в обратном порядке:

(cos Ɵ + i _* сен Ɵ) п = 1 ÷ (cos Ɵ + i _* сен Ɵ) м

(cos Ɵ + i _* сен Ɵ) п = 1 ÷ (cos mƟ + i _* сен мƟ)

Теперь используется, что если z = a + b * i — комплексное число, то 1 ÷ z = a-b * i. Таким образом:

(cos Ɵ + i _* сен Ɵ) п = cos (mƟ) — я _* сен (мƟ).

Используя cos (x) = cos (-x) и -sen (x) = sin (-x), мы имеем:

(cos Ɵ + i _* сен Ɵ) п = [cos (mƟ) — я _* сен (мƟ)]

(cos Ɵ + i _* сен Ɵ) п = cos (- mƟ) + я _* сен (-mƟ)

(cos Ɵ + i _* сен Ɵ) п = cos (nƟ) — я _* сен (n).

Таким образом, можно сказать, что теорема применима ко всем целым значениям «n».

Видео:Высшая математика. Комплексные числа: продолжение. Возведение в степень и извлечение корняСкачать

Решенные упражнения

Видео:Комплексные числа | Операции над комплексными числами | Формула Эйлера | Формула МуавраСкачать

Расчет положительных степеней

Одна из операций с комплексными числами в их полярной форме — это умножение на два из них; в этом случае модули умножаются и аргументы добавляются.

Если у нас есть два комплексных числа z₁ и Z₂ и вы хотите вычислить (z₁ * z₂) 2 , затем действуйте следующим образом:

Распределительное свойство распространяется:

Они сгруппированы, принимая термин «i» как общий фактор выражений:

Как и я 2 = -1, подставляется в выражение:

Реальные члены перегруппированы с реальными, а мнимые с мнимыми:

Наконец, применяются тригонометрические свойства:

Видео:Что такое формула Эйлера для комплексных чисел? Душкин объяснитСкачать

Упражнение 1

Запишите комплексное число в полярной форме, если z = — 2 -2i. Затем, используя теорему Муавра, вычислите z 4 .

Видео:10 класс, 34 урок, Тригонометрическая форма записи комплексного числаСкачать

Решение

Комплексное число z = -2 -2i выражается в прямоугольной форме z = a + bi, где:

Зная, что полярная форма имеет вид z = r (cos Ɵ + i _* sin Ɵ), нам нужно определить значение модуля «r» и значение аргумента «Ɵ». Поскольку r = √ (a² + b²), данные значения подставляются:

r = √ (a² + b²) = √ ((- 2) ² + (- 2) ²)

Затем, чтобы определить значение «Ɵ», применяется его прямоугольная форма, которая задается формулой:

загар Ɵ = (-2) ÷ (-2) = 1.

Поскольку tan (Ɵ) = 1 и a 4 :

z 4 = 2√2 (cos (5Π / 4) + i _* сен (5Π / 4)) 4

= 32 (cos (5Π) + i _* грех (5Π)).

Видео:10 класс, 36 урок, Возведение комплексного числа в степень. Извлечение кубического корняСкачать

Упражнение 2.

Найдите произведение комплексных чисел, выразив его в полярной форме:

z1 = 4 (cos 50 или + я_* сен 50 или )

z2 = 7 (cos 100 или + я_* сен 100 или ).

Затем вычислите (z1 * z2) ².

Видео:✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать

Решение

Сначала формируется произведение заданных чисел:

z₁ z₂ = [4 (cos 50 или + я_* сен 50 или )] * [7 (cos 100 или + я_* сен 100 или )]

Затем модули перемножаются и складываются аргументы:

Наконец, применима теорема Муавра:

(z1 * z2) ² = (28 _* (cos 150 или + (я_* сен 150 или )) ² = 784 (cos 300 или + (я_* сен 300 или )).

Видео:4. Показательная форма комплексного числаСкачать

Расчет отрицательных степеней

Чтобы разделить два комплексных числа z₁ и Z₂ в полярной форме модуль делится, а аргументы вычитаются. Таким образом, фактор равен z₁ ÷ z₂ и выражается это так:

Как и в предыдущем случае, если мы хотим вычислить (z1 ÷ z2) ³, сначала выполняется деление, а затем используется теорема Муавра.

Упражнение 3.

z1 = 12 (cos (3π / 4) + i * sin (3π / 4)),

z2 = 4 (cos (π / 4) + i * sin (π / 4)),

вычислить (z1 ÷ z2) ³.

Решение

Следуя шагам, описанным выше, можно сделать вывод, что:

(z1 ÷ z2) ³ = ((12/4) (cos (3π / 4 — π / 4) + i * sin (3π / 4 — π / 4))) ³

= (3 (cos (π / 2) + i * sin (π / 2))) ³

= 27 (cos (3π / 2) + i * sin (3π / 2)).

Ссылки

1. Артур Гудман, Л. Х. (1996). Алгебра и тригонометрия с аналитической геометрией. Pearson Education.
2. Краучер, М. (s.f.). Теорема Де Муавра для триггерных тождеств. Вольфрам Демонстрационный проект.
3. Хазевинкель, М. (2001). Энциклопедия математики.
4. Макс Петерс, У. Л. (1972). Алгебра и тригонометрия.
5. Перес, К. Д. (2010). Pearson Education.
6. Стэнли, Г. (s.f.). Линейная алгебра. Гроу-Хилл.
7. , М. (1997). Предварительный расчет. Pearson Education.

5 самых популярных легенд и мифов о Такне

Incels: кто они и как думают участники этой группы

11. Формула Муавра. Извлечение корня из комплексного числа

Используя формулу умножения комплексных чисел (3.3), получим формулу возведения комплексного числа в степень, называемую Формулой Муавра:

Из нее следует, что Для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень, а аргумент умножить на показатель этой степени.

Перейдем к процедуре извлечения корней. Известно, что во множестве действительных чисел не из всякого действительного числа можно извлечь корень. Например, 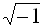не существует. В множестве комплексных чисел дело обстоит иначе.

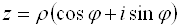
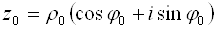
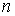
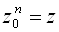
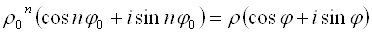
Пусть . Комплексное число называется корнем -й степени из , если , т. е.:

.

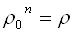
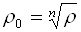
Модуль комплексного числа определяется однозначно, поэтому или (здесь имеется в виду арифметический корень).

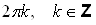
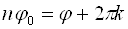
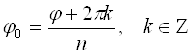
Аргумент комплексного числа определяется с точностью до . Следовательно, , а .

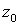
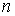
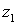
Таким образом, комплексное число , которое является корнем -й степени из имеет вид:

Придавая различные значения, мы не всегда будем получать различные корни. Действительно, можно записать в виде , где . Тогда:

,

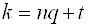
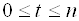
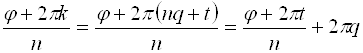
Т. е. значение аргумента при данном отличается от значения аргумента при на число, кратное . Следовательно, в формуле (2) можно ограничится лишь значениями . При таких значениях получаются различные корни, так как разность между их аргументами по абсолютной величине меньше .

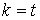
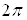
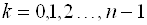
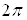
Итак, для каждого ненулевого числа существует ровно корней -й степени из .

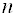
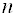
Пример. Вычислить .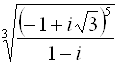

Представим число, стоящее под знаком корня, в тригонометрической форме:

.

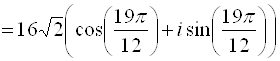
Извлечем далее корень третьей степени из этого комплексного числа:

.

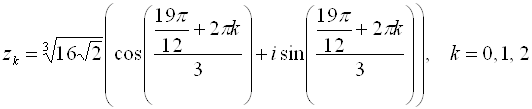
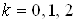
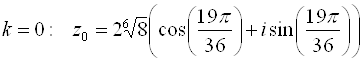
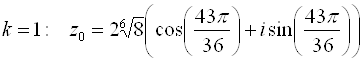
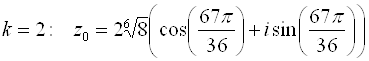
Отсюда полагая, что , получим:

;

;

.

Контрольные Вопросы к лекции №3

1. Счетные и несчетные числовые множества.

2. Ограниченные множества.

3. Границы и грани множеств.

4. Соединения элементов.

5. Вычисление числа размещений, перестановок и сочетаний.

6. Понятие комплексного числа.

7. Понятие мнимой единицы (числа ).

8. Основные операции над комплексными числами.

9. Представление комплексного числа в тригонометрической форме.

10. Понятие модуля комплексного числа.

11. Понятие аргумента комплексного числа.

12. Охарактеризовать умножение и деление комплексных чисел в тригонометрической форме.