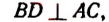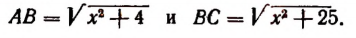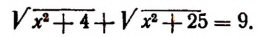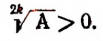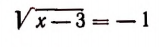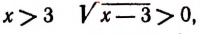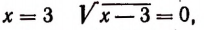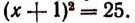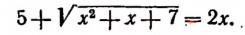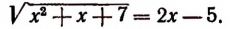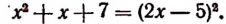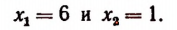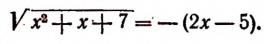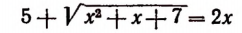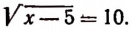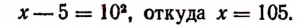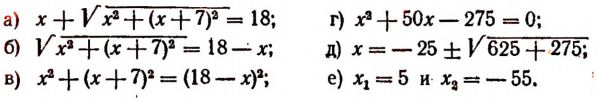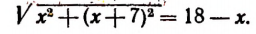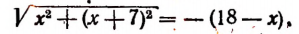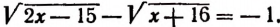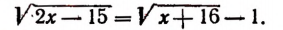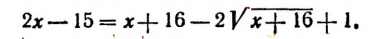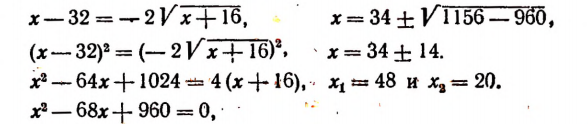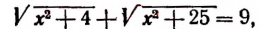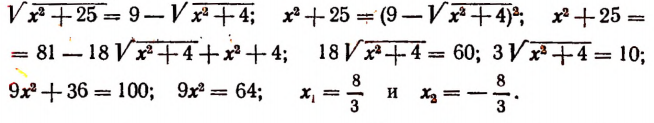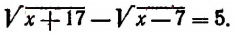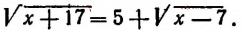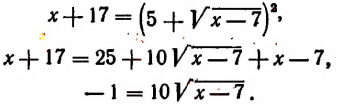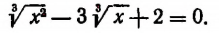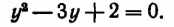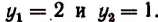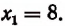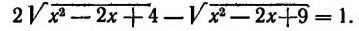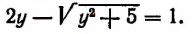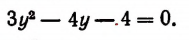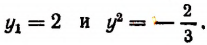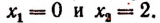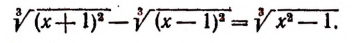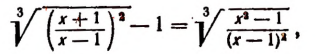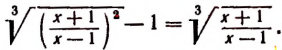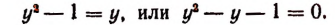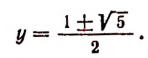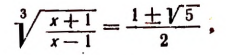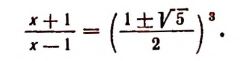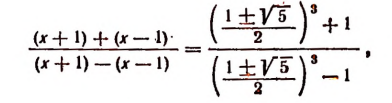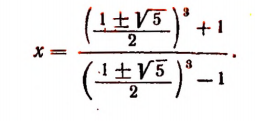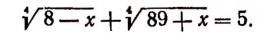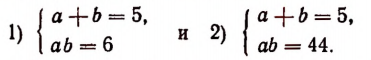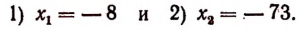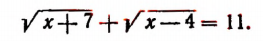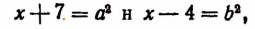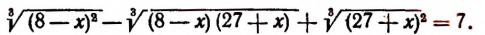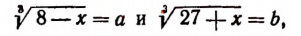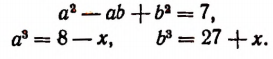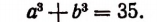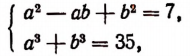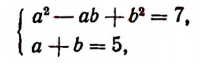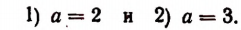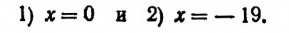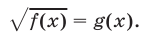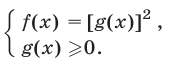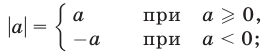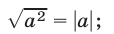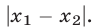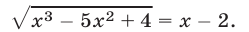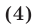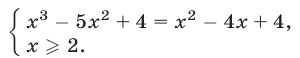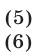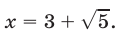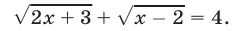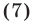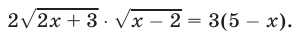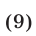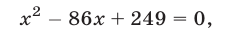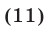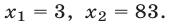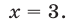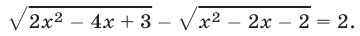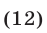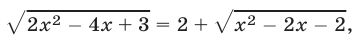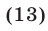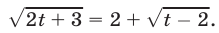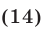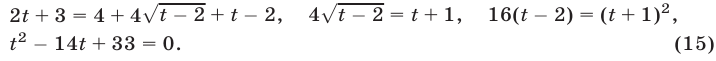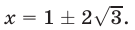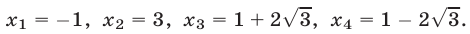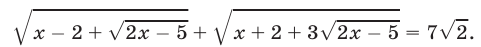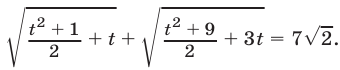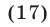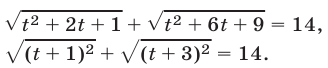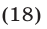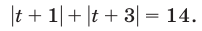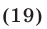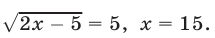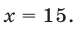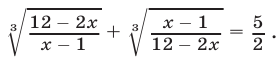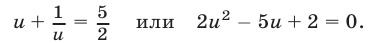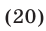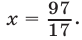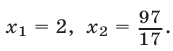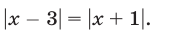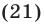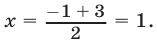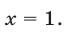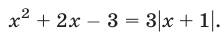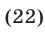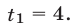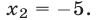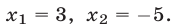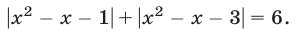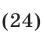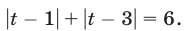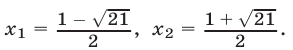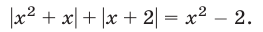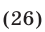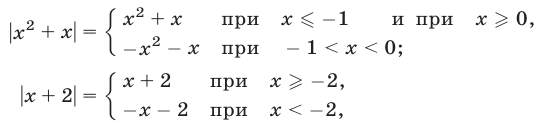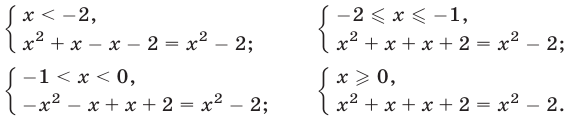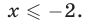Решение иррациональных уравнений с 4 степенью

План урока:

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Иррациональные уравнения

Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.

Приведем примеры иррациональных ур-ний:

Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести

Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.

Видео:Иррациональное уравнение 4(!) степени | Параметр 135 | mathus.ru #егэ2024Скачать

Простейшие иррациональные уравнения

Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:

где а – некоторое число (константа), f(x) – рациональное выражение.

Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:

Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии

n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.

Ответ: корней нет.

Пример. Решите ур-ние

Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:

Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).

Пример. Найдите решение ур-ния

Решение. Возведем обе части в пятую степень:

х 2 – 14х – 32 = 0

Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:

D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324

Итак, нашли два корня: (– 2) и 16.

Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.

Пример. Решите ур-ние

Решение. Возводим обе части во вторую степень:

х – 2 = х 2 – 8х + 16

D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9

Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):

при х = 3 х – 4 = 3 – 4 = – 1

при х = 6 6 – 4 = 6 – 4 = 2

Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.

Пример. Решите ур-ние

Решение. Здесь используется кубический корень, а потому возведем обе части в куб:

3х 2 + 6х – 25 = (1 – х) 3

3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3

Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:

Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.

Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:

при х = 2 1 – х = 1 – 2 = – 1

Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:

Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Уравнения с двумя квадратными корнями

Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.

Пример. Решите ур-ние

Решение. Перенесем вправо один из корней:

Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:

Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:

Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:

(2х – 4) 2 = 13 – 3х

4х 2 – 16х + 16 = 13 – 3х

4х 2 – 13х + 3 = 0

D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121

Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:

Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3

На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.

Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

Введение новых переменных

Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние

Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.

Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:

х 1/2 – 10х 1/4 + 9 = 0

Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид

Это квадратное ур-ние. Найдем его корни:

D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64

Получили два значения t. Произведем обратную замену:

х 1/4 = 1 или х 1/4 = 9

Возведем оба ур-ния в четвертую степень:

(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4

х = 1 или х = 6561

Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:

В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.

Пример. Решите ур-ние

х 1/3 + 5х 1/6 – 24 = 0

Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:

Его корни вычислим через дискриминант:

D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121

Далее проводим обратную заменуx 1/6 = t:

х 1/6 = – 8 или х 1/6 = 3

Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.

Видео:Уравнение четвертой степениСкачать

Замена иррационального уравнения системой

Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.

Пример. Решите ур-ние

Решение. Заменим первый корень буквой u, а второй – буквой v:

Исходное ур-ние примет вид

Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:

Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:

Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:

(х + 6) + (11 – х) = u 3 + v 2

из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:

17 = u 3 + (5 – u) 2

17 = u 3 + u 2 – 10u + 25

u 3 + u 2 – 10u + 8 = 0

Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа

подставим полученные значения в (4):

x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3

x + 6 = 1 или х + 6 = 8 или х + 6 = – 64

х = – 5 или х = 2 или х = – 70

Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим

Корень подошел. Проверяем следующее число, х = 2:

Корень снова оказался верным. Осталась последняя проверка, для х = – 70:

Итак, все три числа прошли проверку.

Видео:Уравнения с корнем. Иррациональные уравнения #shortsСкачать

Уравнения с «вложенными» радикалами

Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:

При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:

Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:

Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:

Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:

Возводим в квадрат и получаем:

х 2 + 40 = (х + 4) 2

х 2 + 40 = х 2 + 8х + 16

И снова нелишней будет проверка полученного корня:

Видео:Ещё один приём решения иррациональных уравнений с корнем третьей степениСкачать

Иррациональные неравенства

По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:

Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.

Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида

Может быть справедливым только тогда, когда

То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во

при четном n можно заменить системой нер-в

Пример. При каких значениях x справедливо нер-во

Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:

х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)

Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во

чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.

Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.

Пример. Найдите решение нер-ва

Решение. Всё очень просто – надо всего лишь возвести обе части в куб:

x 2 – 7x– 8 2 – 7x– 8 = 0

D = b 2 – 4ac = (– 7) 2 – 4•1•(– 8) = 49 + 32 = 81

Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:

Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.

Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.

Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид

Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.

Пример. Решите нер-во

Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):

И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:

D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9

Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.

стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:

f(x) > 0 (подкоренное выражение не может быть отрицательным);

g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).

Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.

Пример. Решите нер-во

Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим

х 2 – 10х + 21 > 0(1)

Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:

Во-вторых, выражение 4 – х не может быть отрицательным:

Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):

Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:

Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:

Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:

Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:

Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).

Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3

Видео:Иррациональные уравнения. 10 класс.Скачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Иррациональное уравнениеСкачать

Калькулятор онлайн.
Решение иррациональных уравнений и неравенств.

Этот математический калькулятор онлайн поможет вам решить иррациональное уравнение или неравенство. Программа для решения иррациональных уравнений и неравенств не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> sqrt(x) — квадратный корень x
x^(1/n) — корень степени n

Введите иррациональное уравнение или неравенство
Решить уравнение или неравенство

Видео:УДИВИТЕЛЬНЫЙ способ решения уравнения 4-ой степениСкачать

Немного теории.

Видео:Иррациональные уравнения и их системы. 11 класс.Скачать

Решение иррациональных уравнений и неравенств

Видео:Решение иррациональных уравнений.Скачать

1. Иррациональные уравнения

Иррациональными называют уравнения, в которых переменная содержится под знаком радикала или под знаком возведения в дробную степень. Для таких уравнений ищут, как правило, только действительные корни.

Основной метод решения иррациональных уравнений — метод возведения обеих частей уравнения в одну и ту же степень. При этом следует иметь в виду, что возведение обеих частей уравнения в одну и ту же нечётную степень есть равносильное преобразование уравнения, а в чётную — НЕравносильное. Значит, основные принципиальные трудности связаны с возведением обеих частей уравнения в одну и ту же чётную степень, когда из-за неравносильности преобразования могут появиться посторонние корни, а потому обязательна проверка всех найденных корней.

ПРИМЕР 1.
( sqrt[Large6normalsize] = sqrt[Large6normalsize] )

Возведя обе части уравнения в шестую степень, получим:
( x^2-5x = 2x-6 Rightarrow )
( x^2-7x +6= 0 Rightarrow )
( x_1=1, ; x_2=6 )
Проверка. «Хорошие» корни можно проверить непосредственной подстановкой в исходное уравнение. При x = 1 заданное уравнение принимает вид ( sqrt[Large6normalsize] = sqrt[Large6normalsize] ), во множестве действительных чисел такое «равенство» не имеет смысла. Значит, 1 — посторонний корень, он появился по причине расширения ОДЗ уравнения после возведения в шестую степень. При х = 6 заданное уравнение принимает вид ( sqrt[Large6normalsize] = sqrt[Large6normalsize] ) — это верное равенство.
Итак, уравнение имеет единственный корень: х = 6.
Ответ: х = 6

Введя новую переменную ( u=x^2-x), получим существенно более простое иррациональное уравнение:
( sqrt+sqrt = sqrt ).
Возведём обе части уравнения в квадрат:
( (sqrt+sqrt)^2 = (sqrt)^2 Rightarrow )
( u+2 +2sqrtsqrt +u+7 = 2u+21 Rightarrow )
( sqrt = 6 Rightarrow )
( u^2+9u+14=36 Rightarrow )
( u^2+9u-22=0 Rightarrow )
( u_1=2, ; u_2=-11 )
Проверка найденных значений их подстановкой в уравнение ( sqrt+sqrt = sqrt ) показывает, что ( u_1=2 ) — корень уравнения, а ( u_2=-11 ) — посторонний корень.
Возвращаясь к исходной переменной x, получаем уравнение ( x^2-x=2 Rightarrow x^2-x-2=0 ), решив которое находим два корня: ( x_1=2, ; x_2=-1 )
Ответ: 2; -1.

Уединение корня и возведение обеих частей уравнения в квадрат привело бы к громоздкому уравнению. В то же время, если проявить некоторую наблюдательность, можно заметить, что уравнение легко сводится к квадратному. Действительно, умножим обе его части на 2:
( 2x^2 +6 -2sqrt = 3x+12 Rightarrow )
( 2x^2 -3x +2 -2sqrt -8 = 0 Rightarrow )

Введя новую переменную ( y=sqrt ), получим: ( y^2-2y-8=0 ), откуда ( y_1=4, ; y_2=-2 ). Значит, исходное уравнение равносильно следующей совокупности уравнений:
( left[begin sqrt =4 \ sqrt = -2 endright. )

Из первого уравнения этой совокупности находим: ( x_1=35; ; x_2=-2 ). Второе уравнение корней не имеет.

Проверка. Так как совокупность уравнений равносильна исходному уравнению, причём второе уравнение этой совокупности корней не имеет, то найденные корни можно проверить подстановкой в уравнение ( sqrt =4). Эта подстановка показывает, что оба найденных значения x являются корнями этого уравнения, а значит, и исходного уравнения.
Ответ: 3,5; -2.

Областью определения уравнения является луч ( [5; ; +infty) ). В этой области выражение ( sqrt ) можно представить следующим образом: ( sqrt = sqrtsqrt ). Теперь уравнение можно переписать так:
( x+x -5 +2sqrtsqrt +2sqrt +2sqrt -48 = 0 Rightarrow ) ( (sqrt)^2 +2sqrtsqrt +(sqrt)^2 +2(sqrt+sqrt) -48 = 0 Rightarrow ) ( (sqrt +sqrt)^2 +2(sqrt+sqrt) -48 = 0 )

Введя новую переменную ( y= sqrt +sqrt ), получим квадратное уравнение ( y^2+2y-48=0 ), из которого находим: ( y_1=6, ; y_2=-8 ). Таким образом, задача свелась к решению совокупности уравнений:
( left[begin sqrt +sqrt =6 \ sqrt +sqrt = -8 endright. )
Из первого уравнения совокупности находим ( x= left( frac right)^2 ), второе уравнение совокупности решений явно не имеет.

Проверка. Нетрудно проверить (подстановкой), что ( x= left( frac right)^2 ) — является корнем уравнения ( sqrt +sqrt =6 ). Но это уравнение равносильно исходному уравнению, значит, ( x= left( frac right)^2 ) — является корнем и исходного уравнения.
Ответ: ( x= left( frac right)^2 )

Иногда при решении иррациональных уравнений оказывается удобным ввести две новые переменные.

ПРИМЕР 5.
( sqrt[Large4normalsize] + sqrt[Large4normalsize] =2 )

Введём новые переменные: ( left<begin u=sqrt[Large4normalsize] \ v=sqrt[Large4normalsize] endright. )

Тогда уравнение примет вид (u+v=2). Но для нахождения значений двух новых переменных одного уравнения недостаточно. Возведя в четвёртую степень обе части каждого из уравнений системы, получим:
( left<begin u^4=1-x \ v^4= 15+x endright. )

Сложим уравнения последней системы: (u^4 +v^4 =16). Таким образом, для нахождения u, v мы имеем следующую симметрическую систему уравнений:
( left<begin u+v=2 \ u^4 +v^4 =16 endright. )
Решив её, находим: ( left<begin u_1=0 \ v_1 =2; endright. ) ( left<begin u_2=2 \ v_2 =0 endright. )

Таким образом, исходное уравнение свелось к следующей совокупности систем уравнений: ( left<begin sqrt[Large4normalsize] =0 \ sqrt[Large4normalsize] =2; endright. ) ( left<begin sqrt[Large4normalsize] =2 \ sqrt[Large4normalsize] =0 endright. )

Решив эту совокупность, находим: (x_1=1, ; x_2=-15 )

Проверка. Проще всего проверить найденные корни непосредственной подстановкой в заданное уравнение. Проделав это, убеждаемся, что оба значения являются корнями исходного уравнения.
Ответ: 1; -15.

ПРИМЕР 6.
( sqrt[Large3normalsize] + sqrt[Large3normalsize] = sqrt[Large3normalsize] )

Возведём обе части уравнения в куб:
( 2x+1 + 3sqrt[Large3normalsize] cdot sqrt[Large3normalsize] + 3sqrt[Large3normalsize] cdot sqrt[Large3normalsize] +6x+1 = 2x-1 Rightarrow ) ( 3sqrt[Large3normalsize] cdot sqrt[Large3normalsize] cdot (3sqrt[Large3normalsize] + sqrt[Large3normalsize] ) = -6x-3 )

Воспользовавшись исходным уравнением, заменим сумму ( sqrt[Large3normalsize] + sqrt[Large3normalsize] ) на выражение ( sqrt[Large3normalsize] ):
( 3sqrt[Large3normalsize] cdot sqrt[Large3normalsize] cdot sqrt[Large3normalsize] = -6x-3 Rightarrow )
( 3sqrt[Large3normalsize] = -2x-1 )
Возведём обе части в куб:
( (2x+1)(6x+1)(2x-1) = -(2x+1)^3 Rightarrow )
( (2x+1)((6x+1)(2x-1) + (2x+1)^2) =0 Rightarrow )
( 16x^2(2x+1) =0 Rightarrow )
( x_1= -05; ; x_2=0 )

Проверка. Подстановкой найденных значений x в исходное уравнение убеждаемся, что его корнем является только x = -0,5.
Ответ: -0,5.

Видео:Как решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать

2. Иррациональные неравенства

Рассмотрим иррациональное неравенство вида ( sqrt 0 ). Осталось лишь заметить, что при одновременном выполнении указанных выше условий обе части заданного иррационального неравенства неотрицательны, а потому их возведение в квадрат представляет собой равносильное преобразование неравенства.

Таким образом, иррациональное неравенство ( sqrt 0 \ f(x) 0 \ x^2-x-12 0 \ x > -12 endright. )

Получаем: ( x geqslant 4)

Ответ: ( x geqslant 4)

Рассмотрим теперь неравенство вида ( sqrt > g(x) ).

Ясно, во-первых, что его решения должны удовлетворять условию ( f(x) geqslant 0 ).
Во-вторых, замечаем, что при ( g(x) g(x) ) не вызывает сомнений.
В-третьих, замечаем, что если ( g(x) geqslant 0 ), то можно возвести в квадрат обе части заданного иррационального неравенства.

Таким образом, иррациональное неравенство ( sqrt > g(x) ) равносильно совокупности систем неравенств:
( left<begin f(x) geqslant 0 \ g(x) (g(x))^2 endright. )

Во второй системе первое неравенство является следствием третьего, его можно не писать.

Данное неравенство равносильно совокупности систем неравенств:
( left<begin x^2-x-12 geqslant 0 \ x 0 )

Преобразуем неравенство к виду ( x^2+3x-10 +3sqrt >0 ) и введём новую переменную ( y= sqrt ). Тогда последнее неравенство примет вид ( y^2+3y-10 >0 ), откуда находим, что либо (y 2).

Таким образом, задача сводится к решению совокупности двух неравенств:
( left[begin sqrt 2 endright. )

Первое неравенство не имеет решений, а из второго находим:
( x^2+3x >4 Rightarrow )
( (x+4)(x-1) >0 Rightarrow )
( x 1 )
Ответ: ( x 1 ).

Видео:Иррациональные уравнения — часть 1Скачать

Иррациональные уравнения в математике с примерами решения и образцами выполнения

Задача:

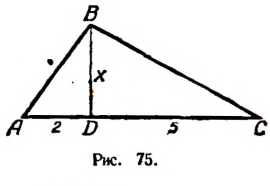
В треугольнике ABC (рис. 75):

AD = 2 см, DC = 5 см,
АВ + ВС = 9 см.
Найти BD.

Решение:

Пусть длина отрезка BD равна х см. Тогда

Получилось уравнение, в котором неизвестное входит в подкоренное выражение. Такое уравнение называется иррациональным. Решение этого уравнения приведено на странице 310.

Определение:

Уравнение, в котором неизвестное входит в какое-либо выражение, стоящее под знаком корня, называется иррациональным.

Во многих случаях иррациональное уравнение, как это ниже показано на примерах, может быть преобразовано в рациональное, являющееся его следствием. Но прежде чем показать это на примерах, мы изложим предварительные сведения, необходимые для понимания процесса решения иррациональных уравнений.

1. Всякий корень четной степени из положительного числа, входящий в иррациональное уравнение, мы будем считать, как и раньше, арифметическим. Поясним это. Если А > 0 и в иррациональное уравнение входит 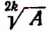, то всегда будем считать, что

Принимая во внимание сказанное выше, мы должны считать, что, например, уравнение

не имеет корней. Действительно,

при
при
при 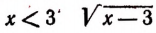— мнимое число.

Таким образом, 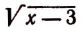никогда не может равняться числу — 1, а это и значит, что уравнение

корней не имеет.

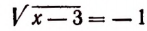
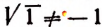
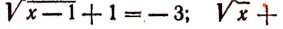
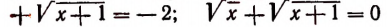
Было бы ошибкой считать число 4 корнем уравнения , так как . Аналогично можно убедиться, что ни одно из следующих уравнений также не имеет корней.

Теорема:

Если обе части уравнения А=В возвысить в квадрат, то полученное уравнение 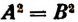будет иметь своими корнями все корни данного уравнения А = В и корни уравнения А = — В, (Уравнение А = —В будем называть сопряженным уравнению А = В.) Но прежде чем доказывать эту теорему, поясним ее содержание на примере. Рассмотрим уравнение х + 1 = 5 и уравнение, ему сопряженное, т. е. х + 1 = —5. У первого уравнения имеется единственный корень 4, а у второго —6. Возведя левую и правую части уравнения х + 1 = 5 в квадрат, получим, что

Решив это уравнение, убедимся, что его корнями будут числа 4 и — 6, т. е. только корни данного уравнения х + 1 = 5 и сопряженного ему уравнения х + 1 = —5 .

Как раз в этом и заключается смысл сформулированной выше теоремы.

Доказательство:

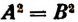
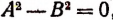
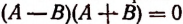
Уравнение равносильно уравнению , или уравнению . Но. это последнее уравнение удовлетворяется как при А = В, так и при А = — В и никогда больше. Теорема доказана.

Следствие:

Из доказанной теоремы вытекает, что при переходе от уравнения А = В к уравнению 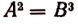потери корней не произойдет, но могут появиться посторонние корни, а именно корни уравнения
А = —В.

Если окажется, что уравнение А = — В не имеет корней, то не появляется и посторонних корней.

Видео:Система иррациональных уравнений #4Скачать

Иррациональные уравнения, содержащие только один радикал

Уединив корень, получим:

Возведем обе части этого уравнения в квадрат. В результате получим рациональное уравнение

Решив последнее уравнение, получим, что

Теперь необходимо проверить, являются ли числа 6 и 1 корня-ми данного уравнения. Проверка показывает, что число 6 является корнем уравнения , а число 1 его корнем не является. Мы возводили в квадрат левую и правую части уравнения . Значит, число 1 есть корень сопряженного уравнения, т. е. уравнения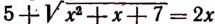

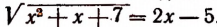
Итак, иррациональное уравнение

имеет лишь один корень, равный числу 6.

Возьмем еще одно уравнение, содержащее только один радикал, а именно:

Здесь корень уже уединен. Поэтому, возведя обе части уравнения в квадрат, получим:

Проверка показывает, что число 105 является корнем данного уравнения. Здесь мы не получили постороннего корня, потому что сопряженное уравнение, т. е. уравнение 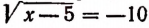, корней не имеет.

Примеры:

Проверка показывает, что оба числа 5 и —55 являются корнями уравнения

Значит, сопряженное уравнение, т. е. уравнение

корней не имеет.

Видео:Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать

Уравнения, содержащие два квадратных радикала

Пример:

Уединим один из корней:

Возведем в квадрат левую и правую части последнего уравнения:

Уединим один оставшийся корень:

Проверкой устанавливаем, что данное уравнение 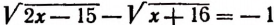имеет только один корень, равный числу 20.

Пример:

В качестве второго примера решим уравнение

составленное по условиям задачи, поставленной в начале настоящей главы.

Легко убедиться, что оба числа являются корнями уравнения . Но мы знаем, что не всякий корень уравнения, составленного по условиям задачи, обязательно должен являться и решением самой задачи. В данном случае решением задачи будет только положительный корень . Значит, искомая высота BD треугольника ABC будет равна см.

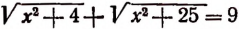
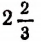
Пример:

Уединим один из корней:

Возведем в квадрат левую и правую части этого уравнения:

Последнее уравнение корней не имеет, ибо его левая часть есть отрицательное число, а правая часть ни при каком значении х не может быть числом отрицательным. Значит, и первоначальное уравнение корней не имеет.

Видео:Решение иррациональных уравнений: возведение в степеньСкачать

Искусственные приемы решения иррациональных уравнений

Пример:

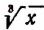
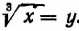
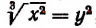
Примем новое неизвестное и положим, что Тогда и данное уравнение примет вид: ^-3(/ + 2 = 0.

Отсюда

Приняв 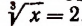, получим, что

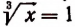
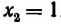
Приняв затем . получим, что . Оба числа 8 и 1 являются корнями данного уравнения.

Пример:

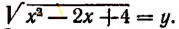
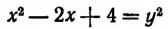
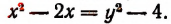
Положим, что Тогда и Относительно нового неизвестного у данное уравнение примет вид:

Освободившись от корня, получим:

Отсюда

Значение следует отбросить, так как буквой у мы
обозначили 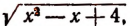который отрицательных значений принимать не может.

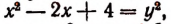
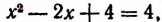
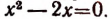
Взяв у = 2 и подставив это значение неизвестного у в уравнение получим или Откуда

Числа 0 и 2 являются корнями первоначального уравнения. Других действительных корней данное уравнение не имеет.

Пример:

Подстановкой убеждаемся, что 1 не есть корень данного уравнения. Поэтому, разделив обе части уравнения на 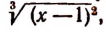получим уравнение

После сокращения последнее уравнение принимает вид:

Обозначив 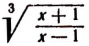через у, получим:

Составим производную пропорцию, воспользовавшись тем, что сумма членов первого отношения так относится к их разности, как сумма членов второго отношения к их разности. Получим, что

Видео:Иррациональные уравнения. 10 классСкачать

Способ решения иррационального уравнения с помощью системы рациональных уравнений

Решение всякого иррационального уравнения можно свести к решению соответствующей системы рациональных уравнений. Общий метод, позволяющий это сделать, покажем на примерах.

1. Решить уравнение

Пользуясь тем, что

и тем, что 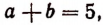получим уравнение

Отсюда 1) аb = 6 и 2) аb = 44.

Теперь остается решить две системы:

Первая система дает а = 2, b = 3 и а = 3, b = 2.
Вторая система действительных решений не имеет.

Пользуясь, например, уравнением 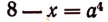и полученными значениями неизвестного а, найдем действительные корни данного иррационального уравнения:

2. Решить уравнение:

или равносильную ей систему:

Отсюда а = 6.

Из уравнения 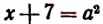находим, что х = 29.

3. Решить уравнение:

Из последних двух равенств будем иметь:

илн равносильную ей систему:

Пользуясь уравнением 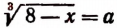и найденными значениями неизвестного а, найдем корни первоначального уравнения:

Видео:10 класс. Алгебра. Решение иррациональных уравнений.Скачать

Дополнение к иррациональным уравнениям и примеры с решением

Уравнения, в которых переменная находится под знаком корня, называются иррациональными. Решение иррациональных уравнений сводится к переходу от иррационального уравнения к рациональному путем возведения обеих частей уравнения в степень, равную показателю степени корня. Если показатель степени четный, то необходимо либо предварительно выписывать ограничения: подкоренное выражение должно быть неотрицательным, выражение, равное арифметическому корню, также должно быть неотрицательным, т. к. в четную степень без приобретения посторонних корней можно возводить только неотрицательные выражения, либо делать проверку полученных решений.

Этот материал взят со страницы решения задач по математике:

Возможно вам будут полезны эти страницы:

Видео:Система иррациональных уравнений #1Скачать

Уравнения, содержащие знак модуля

1.Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо равносильно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного.

При решении иррациональных уравнений необходимо учитывать следующее:

1) если показатель радикала — четное число, то подкоренное выражение должно быть неотрицательным; при этом значение радикала также является неотрицательным;

2) если показатель радикала — нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак радикала совпадает со знаком подкоренного выражения.

Рассмотрим уравнение вида

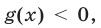
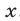
Если то уравнение (1) не имеет корней, так как левая часть уравнения (1) не может принимать отрицательные значения ни при каких значениях .

Если же 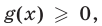то при возведении обеих частей уравнения (1) в квадрат получим равносильное уравнение. Таким образом, уравнение (1) равносильно системе

Замечание:

При решении уравнения (1) нет необходимости предварительно находить ОДЗ левой части (1), решая неравенство 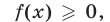которое может оказаться довольно сложным. Достаточно найти корни уравнения (2) и, не прибегая к непосредственной подстановке этих корней в уравнение (1), выяснить, какие из найденных корней удовлетворяют неравенству (3). Эти корни, и только они, являются корнями уравнения (1).

2.Из определения модуля (абсолютной величины) числа следует, что

1)

2)

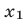
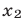
3) если и — произвольные точки числовой оси, то расстояние между ними равно

Пример:

Решение:

Уравнение (4) равносильно системе

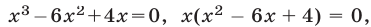
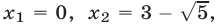
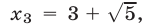
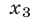
Уравнение (5), равносильное каждому из уравнений имеет корни из которых лишь корень удовлетворяет условию (6).

Ответ.

Пример:

Решение:

Возведя обе части уравнения (7) в квадрат, получим уравнение

равносильное (7), так как обе части уравнения (7) неотрицательны. Уравнение (8) равносильно уравнению

Возведя в квадрат обе части уравнения (9), получим уравнение

которое имеет корни

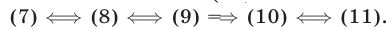
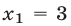
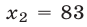
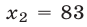
Заметим, что уравнение (11) является следствием уравнения (7), так как Число — корень уравнения (7), а число — посторонний корень для уравнения (7): при левая часть уравнения (7) больше четырех.

Ответ.

В рассмотренном примере можно было сначала перенести один из радикалов в правую часть уравнения (метод уединения радикала), а затем возвести обе части полученного уравнения в квадрат.

Воспользуемся этим приемом при решении следующего примера.

Пример:

Решение:

Применив метод уединения радикала, получим уравнение

равносильное уравнению (12).

Заметим, что нет необходимости находить ОДЗ уравнения (13), но следует обратить внимание на подкоренные выражения. Если ввести новое неизвестное (выполнить замену переменной), полагая 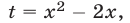, то уравнение (13) при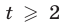мет вид

При (в ОДЗ уравнения (14)) это уравнение равносильно каждому из уравнений

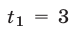
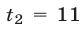
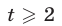
Корни и уравнения (15) удовлетворяют условию и поэтому являются корнями уравнения (14).

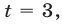
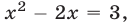
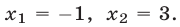
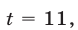
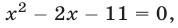
Если то откуда Если то откуда

Ответ.

В примерах 1-3 был использован метод возведения обеих частей уравнения в квадрат. В отдельных случаях применяются другие приемы, которые могут оказаться более эффективными.

Пример:

Решение:

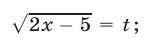
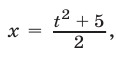
Положим тогда и уравнение (16) примет вид

Уравнение (17) равносильно каждому из уравнений

Используя тождество 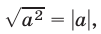запишем уравнение (18) в виде

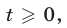
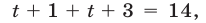
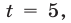
Так как то уравнение (18) и равносильное ему уравнение (19) можно записать в виде откуда т. е.

Ответ.

Пример:

Решение:

Полагая 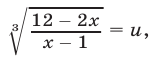преобразуем уравнение к виду

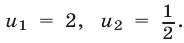
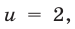
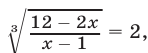
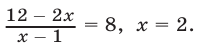
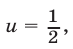
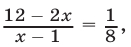
Уравнение (20) имеет корни Если то откуда Если то откуда

Оба найденных корня являются корнями исходного уравнения, так как в процессе решения было использовано (наряду с заменой неизвестного) только преобразование вида 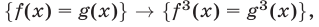при котором получается равносильное уравнение.

Ответ.

Пример:

Решение:

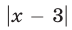
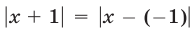
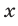
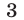
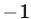
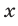
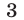
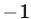
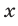
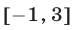
Так как и — это расстояния от искомой точки до точек и соответственно, то из равенства (21) следует, что искомая точка находится на одинаковом расстоянии от точек и . Таким образом, точка — середина отрезка и поэтому

Ответ.

Пример:

Решение:

Полагая 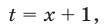получаем уравнение

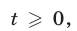
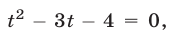
Если то (23) имеет вид откуда находим

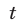
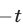
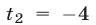
Поскольку при замене на уравнение (23) не меняется, число также является корнем уравнения (23), а корни уравнения (2) — числа и

Ответ.

Пример:

Решение:

Положим 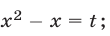тогда уравнение (24) примет вид

Решить уравнение (25) — значит найти все такие точки числовой оси (рис. 8.1), для которых сумма расстояний от каждой из них до точек 1 и 3 равна 6. Заметим, что искомые точки лежат вне отрезка [1,3], так как сумма расстояний от любой точки отрезка до его концов равна 2.

Пусть — искомая точка, лежащая правее точки 3; -расстоя-ние от точки до точки 3, — сумма расстояний от точки до точек 3 и 1. Тогда откуда а точке соответствует число Аналогично, корнем уравнения (25) является точка находящаяся на расстоянии 2 от точки 1.

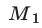
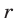
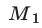
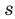
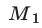
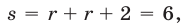
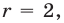
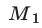
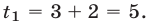
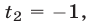
Таким образом, задача сводится к решению уравнений 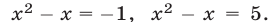Первое из них не имеет действительных корней, а второе имеет два корня.

Ответ.

Пример:

Решение:

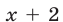
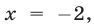
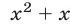
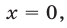
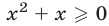
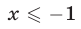
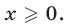
Функция меняет знак при а функция — при и причем при и Поэтому

а уравнение (26), записанное без знака модуля на промежутках 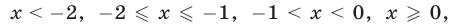равносильно совокупности следующих систем:

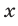
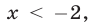
Первой из этих систем удовлетворяют все значения из промежутка второй системе — значение остальные две системы не имеют решений.

Ответ.

Решение иррациональных уравнений

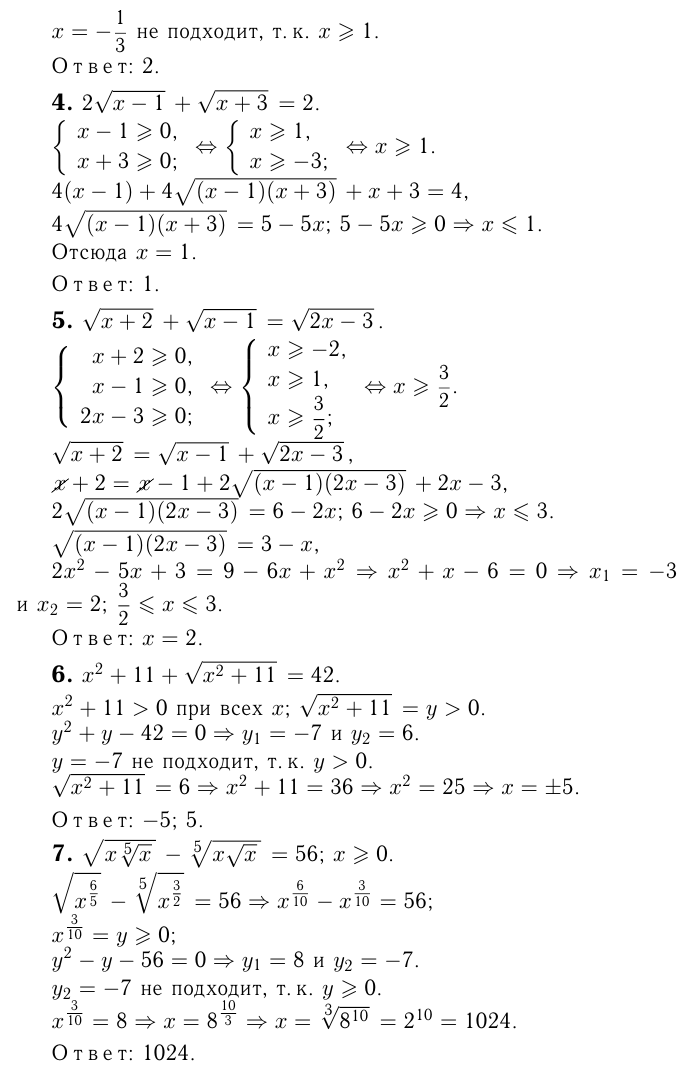
Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института