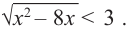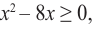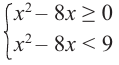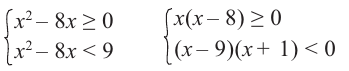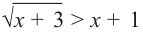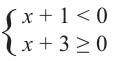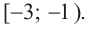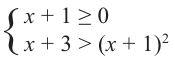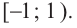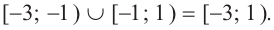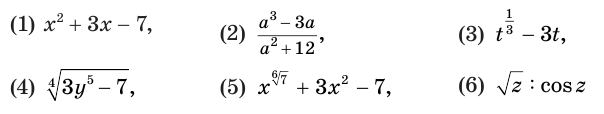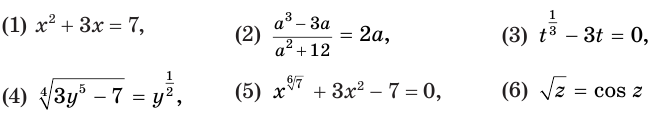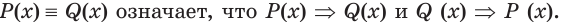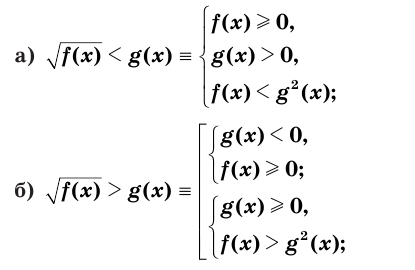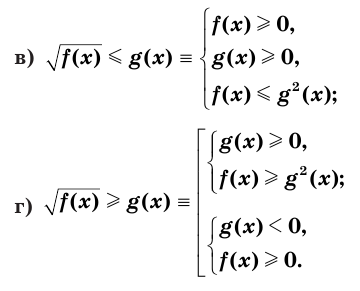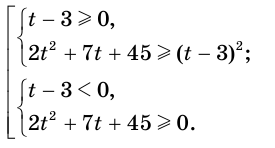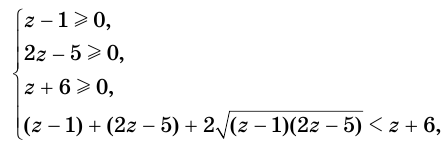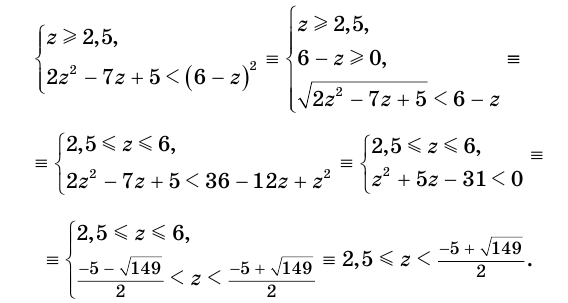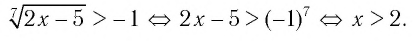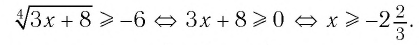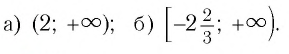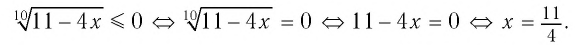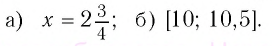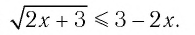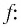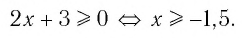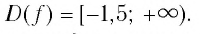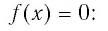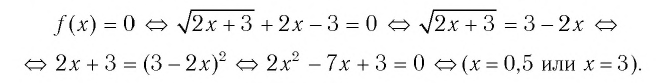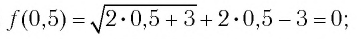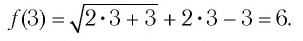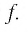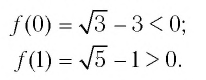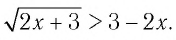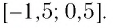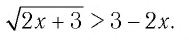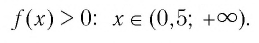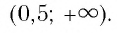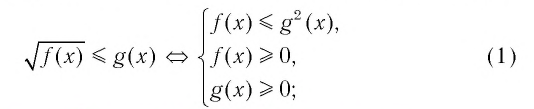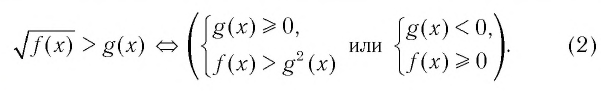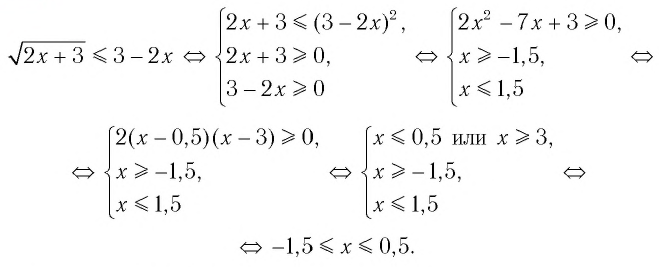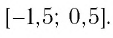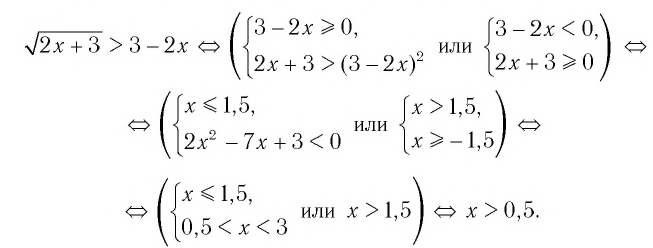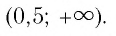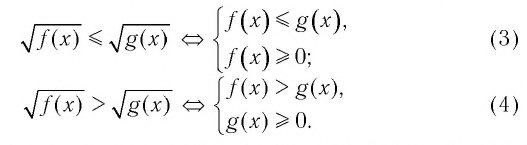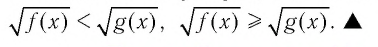Решение иррациональных уравнений методом интервалов

Неравенства, содержащие переменную под знаком радикала, называются иррациональными неравенствами.

Содержание:

Решение иррациональных неравенств также ищут на множестве действительных чисел и, используя свойства корня и неравенств, сводится к решению системы рациональных неравенств.

Пример: Решите неравенство

Решение: чтобы найти множество решений данного неравенства на множестве допустимых значений, т. е. при условии

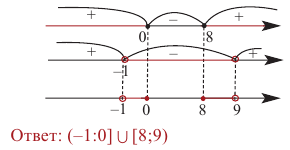
Каждое неравенство системы решим методом интервалов и найдем пересечение полученных решений:

Пример: Решите неравенство

Решение: рассмотрим два случая, в зависимости от знака правой части.

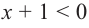
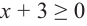
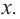
1) при для всех неравенство справедливо для всех Значит, надо решить систему

Ее решением является промежуток

2) при 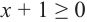обе стороны заданного неравенства можно возвести в квадрат. Тогда получим систему

Ее решением является промежуток

Решением заданного неравенства является

Видео:Решение неравенства методом интерваловСкачать

Способы решения иррациональных неравенств

С действием возведения в степень связаны разные виды выражений. Будем рассматривать выражения с переменными, при образовании которых используются действия сложения, вычитания, умножения, деления и возведения в степень, причем возведение в степень хотя бы один раз применено к выражению с переменной.

Если показатель степени целый, то возникает рациональное выражение, если дробный, то — иррациональное выражение, а если иррациональный, то — трансцендентное выражение.

К трансцендентным выражениям приводят и действия нахождения значений синуса, косинуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса, арккотангенса. Рациональные и иррациональные выражения вместе составляют множество алгебраических выражений.

выражения (1) и (2) являются рациональными, выражения (3) и (4) — иррациональными, выражения (5) и (6) — трансцендентными, а выражения (1)—(4) — алгебраическими.

В зависимости от того, из каких выражений составлено уравнение, говорят о рациональных, иррациональных, трансцендентных уравнениях.

уравнения (1) и (2) являются рациональными, уравнения (3) и (4) — иррациональными, а уравнения (5) и (6) — трансцендентными.

Так же говорят о рациональных, иррациональных, трансцендентных неравенствах.

В этом параграфе рассматривается решение иррациональных уравнений и неравенств. При их решении нужно следить за тем, какие преобразования выполняются при этом.

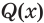
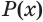
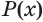
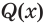
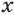
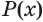
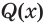
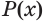
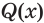
Утверждение равносильно утверждению , если утверждения и истинны при одних и тех же значениях переменной . Равносильность уравнений означает, что они имеют одни и те же корни, а равносильность неравенств — то, что они имеют одни и те же решения. Равносильность утверждений и обозначают = .

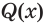
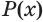
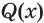
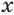
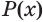
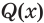
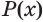
Утверждение следует из утверждения , если утверждение истинно при всех значениях переменной , при которых истинно утверждение . Следование второго уравнения из первого означает, что каждый корень первого уравнения является корнем второго уравнения, но второе уравнение может иметь и дополнительные корни. Так же понимается и следование одного неравенства из другого. Следование утверждения из утверждения обозначают .

Отношения равносильности и следования связаны:

При решении иррациональных неравенств нужно учитывать, что проверка подстановкой найденного множества чисел обычно невозможна из-за его бесконечности. Поэтому при решении неравенств нужно следить за равносильностью проводимых преобразований.

Теорема:

Верны следующие равносильности:

Доказательство проводится по схеме, использованной при доказательстве теоремы 9 с применением соответствующих свойств числовых неравенств.

Пример №1

Решим неравенство 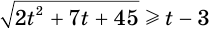. Это неравенство равносильно совокупности неравенств

Первую систему можно заменить равносильной системой 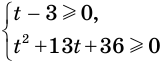, которая равносильна системе , которая, в свою очередь, равносильна неравенству .

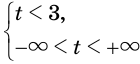
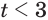
Вторая система совокупности равносильна системе , которая равносильна неравенству .

Решения данного неравенства получим, когда объединим решения и первой и второй систем совокупности, в результате получим множество всех действительных чисел.

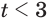
Ответ. .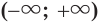

Пример №2

Решим неравенство .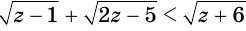

Обратим внимание на то, что на области определения левая и правая части данного неравенства обе неотрицательны, поэтому оно равносильно системе неравенств

решение которой следующее:

Ответ. .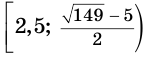

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Какие неравенства называются иррациональными

В этой лекции мы будем рассматривать неравенства, содержащие переменную (неизвестное) под знаком корня. Такие неравенства называются иррациональными.

При решении иррациональных неравенств часто используют подход, который мы уже применяли, решая иррациональные уравнения. Он состоит в замене исходного неравенства равносильным ему неравенством (системой или совокупностью неравенств).

Пример №3

Решение:

а) Учитывая свойства корня нечетной степени, получаем:

б) По определению корня четной степени значения выражения

неотрицательны при всех значениях при которых это

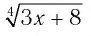
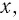
выражение имеет смысл, т. е. когда значения подкоренного выражения неотрицательны. Таким образом, имеем:

Ответ:

Пример №4

Решение:

а) По определению корня четной степени значения выражения 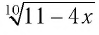отрицательными быть не могут. Поэтому имеем:

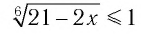
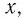
б) Поскольку обе части неравенства неотрицательны при всех значениях при которых его левая часть имеет смысл, то имеем:

Ответ:

При решении иррациональных неравенств часто используется также метод интервалов.

Пример №5

Решить неравенство

Решение:

Обозначим 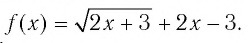Найдем область определения функции

Таким образом,

Найдем нули функции 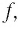т. е. корни уравнения

Проверка:

Значит, 0,5 — единственный нуль функции

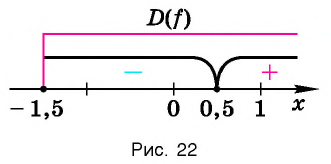
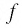
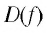
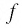
Отметим нуль функции на области определения (рис.22). Определим знаки значений функции на образовавшихся интервалах, для чего вычислим:

Используя рисунок 22, запишем решение неравенства

Ответ:

Пример №6

Решить неравенство

Решение:

Решение этого примера аналогично решению примера 3.

Используя рисунок 22, записываем решение неравенства

Ответ:

▲ При решении иррациональных неравенств часто используются следующие утверждения о равносильности неравенств и систем неравенств:

Решим пример 3, используя равносильность (1):

Ответ:

Решим пример 4, используя равносильность (2):

Ответ:

Для решения заданий такого типа, как, например, в 1.265, можно использовать следующие утверждения о равносильности:

Аналогичные утверждения можно записать и для неравенств

• Производная в математике
• Как найти производную функции
• Асимптоты графика функции
• Касательная к графику функции и производная
• Формулы преобразования суммы и разности синусов (косинусов) в произведение
• Корень n-й степени из числа и его свойства
• Свойства и график функции y=ⁿ√x (n>1, n∈N)
• Иррациональные уравнения

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:иррациональные неравенства методом интервалов 1Скачать

Решение иррациональных неравенств методом интервалов

Разделы: Математика

Учащиеся сельских школ не имеют возможности обучаться в специализированных классах или в классах с углубленным изучением математики, поэтому с детьми, которым нравится математика, мы более глубоко изучаем темы, не вошедшие в обязательную программу, но знания которых позволяют им успешно справиться с заданиями ЕГЭ и тем самым без проблем поступить в ВУЗы и продолжить образование. Одной из таких тем является “Решение иррациональных уравнений и неравенств”. Если решение иррациональных уравнений в некоторых школьных учебниках рассматривается, то решение иррациональных неравенств нет. Я хочу предложить вам разработку урока по теме “Решение иррациональных неравенств методом интервалов”, который я проводила для учащихся 9–10-х классов.

Для изучения выбрала этот метод, т.к. при его использовании повторяется решение иррациональных уравнений.

ХОД УРОКА

I. Приветствие учителя, обоснование темы и цели урока.

Тема, с которой я вас хочу познакомить, поможет при сдаче ЕГЭ и непременно понадобится вам для продолжения образования. А в том, что вы захотите его продолжить, я ничуть не сомневаюсь. Надеюсь, что наше сотрудничество будет полезным и для вас и для меня.

Я желаю вам успехов в сегодняшней работе и хочу привести вам слова великого Микеланджело: “Если бы люди знали, как много я тружусь, чтобы добиться мастерства, они перестали бы считать меня таким уж талантливым”. Слайд 1.

Действительно, только упорный труд приводит нас к успеху. Мне бы очень хотелось, чтобы на сегодняшнем уроке вы это почувствовали. Кто из вас сейчас может с уверенностью сказать: “Я знаю все досконально и могу без труда решать иррациональные неравенства методом интервалов?” Пожалуй, никто. Я, например, готовясь к сегодняшнему уроку, еще много нового открыла для себя, и хочу этим поделиться с вами.

Открываем тетради, записываем дату и тему урока. Слайд 2.

Тема: Решение иррациональных неравенств методом интервалов

Цель урока:

1. Усвоить алгоритм решения иррациональных неравенств методом интервалов.
2. Научиться решать иррациональные неравенства с применением алгоритма. Слайд 3

II. Итак, перейдем к реализации нашей цели:

Вспомним определение иррационального неравенства: Слайд 4.

Иррациональным называют неравенства, в которых переменные входят под знак корня.

Совместная работа учителя и учащихся при разборе решения иррациональных неравенств методом интервалов.

Решим неравенства: Слайд 5

1)

2)

3)

Разберем решение неравенств: Слайды 6–9.

1. равносильно

Шаг 1. Рассмотрим иррациональную функцию и найдем область определения

— область определения

Шаг 2. Вычислим нули функции

— нуль функции

Шаг 3. На координатной прямой отмечаем нуль функции принадлежащий области определения. Получается два промежутка: [5;6) и (6;+). Определяем знак функции на каждом промежутке. Выписываем промежуток, на котором

Ответ:

2. равносильно

Шаг 1. Рассмотрим иррациональную функцию , найдем область определения

— область определения

Шаг 2. Вычислим нули функции

— нуль функции

Шаг 3. На координатной прямой отмечаем нуль функции, принадлежащий области определения. Получаем два промежутка [-7;2) и (2;+). Определяем знак функции на каждом промежутке. Выписываем промежуток на котором .

Ответ:

3.

Шаг 1. Рассмотрим иррациональную функцию , найдем область определения

и область определения.

Шаг 2. Вычислим нули функции

-1; 1; 2 – нули функции

Шаг 3. На координатной прямой отмечаем нули функции, принадлежащие области определения, получается два промежутка (-;-1] и [2;+). Определяем знак функции на каждом промежутке и выписываем промежуток на котором

Ответ: и

III. Итак, мы рассмотрели с вами решение трех неравенств. Вы проследили порядок выполнения заданий. Какие вопросы появились по ходу объяснения? Если нет вопросов, то попробуйте сами сформулировать алгоритм решения иррационального неравенства методом интервала. (учащиеся сами формулируют этапы решения иррационального неравенства). Затем на экран проецируется алгоритм, и, учащиеся проговаривают этапы решения, особое внимание уделяется третьему этапу.

Алгоритм решения иррациональных неравенств. Слайд 10

1. Рассмотрим иррациональную функцию; найдем область определения функции.
2. Вычислим нули функции.
3. На координатной прямой:

• отметим нули функции, принадлежащие области определения;
• определим знак функции на каждом промежутке;
• с учетом знака неравенства выпишем ответ.

Сейчас мы перейдем к очень ответственному моменту, вы будете самостоятельно решать задания с применением приведенного алгоритма. Я предлагаю вам двигаться в своем собственном темпе.

(Во время самостоятельной работы проходит по рядам и смотрит, как ребята справляются с заданиями, выделяет для себя группу контроля. Если возникает необходимость дает незначительные консультации на местах)

IV. Задания для самостоятельной работы: Слайд 11

1.

2.

3.

V. Затем на экран проецируется пошаговая проверка. За каждый правильный шаг, учащиеся ставят себе плюс. Каждое задание оценивается отдельно.

Проверяем: Слайд 12

1 неравенство:

1 шаг

2 шаг

3 шаг

2 неравенство

1 шаг и

2 шаг

3 шаг

3 неравенство

1 шаг

2 шаг и

3 шаг

На экран проецируем критерии оценки. Слайд 13

• 5 баллов – задание выполнено полностью и верно.
• 4 балла – задание верно выполнено на первом и втором шаге. Допущена ошибка в вычислениях на третьем шаге.
• 3 балла — задание верно выполнено на первом шаге, вычислительная ошибка на втором шаге.
• В остальных случаях – 2 балла.

VI. Затем каждый ученик получает лист самоконтроля, на котором дано полное решение всех трех неравенств, и с его помощью, устраняет ошибки, допущенные в своей работе.

VII. Подводятся итоги урока и дается задание на дом с ответами. Cлайд 14

1. Ответ

2. Ответ

3. Ответ

Видео:Алгебра 9. Урок 7 - Неравенства. Метод интервалов - основные фактыСкачать

Решение комбинированных неравенств методом интервалов

Решение комбинированных неравенств методом интервалов

В этой статье я расскажу, как решать неравенства вида V, где P(x) и G(x) — произвольные функции, а V — один из знаков >,

Собственно, и вся премудрость.

=0 » title=»<sqrt-x-2>/<sqrt-x-1>>=0 «/>

Начнем с нахождения ОДЗ.

Подкоренное выражение может принимать только неотрицательные значения, и знаменатель дроби не может быть равен нулю. Получим систему неравенств:

=0> =0> <sqrt-x-10>>> » title=»delim<matrix<=0> =0> <sqrt-x-10>>> «/>

Вспомним об этой системе чуть позже.

Теперь нам нужно найти точки, в которых выражение, стоящее в левой части неравенства меняет знак — это нули числителя и знаменателя.

Чтобы их найти, нам нужно решить два иррациональных уравнения:

и

Решим первое уравнение. Оно равносильно системе:

=0> >> » title=»delim<matrix<<sqrt=x+2> =0> >> «/>

=0> >> » title=»delim<matrix <=0> >> «/>

Решим первое уравнение системы:

. Корень этого уравнения удовлетворяет условию =0″ title=»x+2>=0″/>.

Внимание! Корень х=3 — корень четной кратности. В этом месте нужно быть внимательными — в корнях четной кратности функция знак не меняет.

Решим второе уравнение . Оно равносильно системе:

=0> >> » title=»delim<matrix<<sqrt=x+1> =0> >> «/>

=0> >> » title=»delim<matrix <=0> >> «/>

Решим первое уравнение системы:

. Корни этого уравнения и удовлетворяют условию =0″ title=»x+1>=0″/>.

Нанесем корни числителя и знаменателя на числовую ось. Вспомним, что точки, соответствующие корням знаменателя мы всегда «выкалываем» (тем самым мы учтем последнее условие ОДЗ), а корни числителя в случае нестрогого неравенства закрашиваем:

Теперь самое время вспомнить об ОДЗ. Оно представляет из себя систему неравенств:

=0> =0> <sqrt-x-10>>> » title=»delim<matrix<=0> =0> <sqrt-x-10>>> «/>

Последнее условие системы мы учли, «выколов» нули знаменателя. Первые два условия: =1/2″ title=»x>=1/2″/> и =3/7″ title=»x>=3/7″/>

Теперь нужно аккуратно расставить знаки. В нашем случае знаки не столь очевидны, как при решении рациональных неравенств.

Возьмем число, больше большего корня, например, 10. (Мы можем это сделать, так как х=10 принадлежит ОДЗ неравенства) Подставим число 10 вместо х в левую часть неравенства, и выясним, какой знак она принимает в этой точке.

Числитель и знаменатель дроби отрицательны, поэтому вся дробь больше нуля, т.е. левая часть неравенства при х=10 больше нуля. Теперь расставим знаки, учитывая, что в точке х=3 смены знака не происходит.

Нас интересует промежуток, где выполняется условие ≥0.

Внимание! В случае нестрогого неравенства условие равенства нулю проверяем отдельно, то есть при записи ответа не забываем х=3.

Ответ: [)

И, в заключение, я предлагаю вам посмотреть видеоурок с решением неравенства

И.В. Фельдман, репетитор по математике.

📽️ Видео

Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА неравенства с корнемСкачать

Неравенства. Метод интервалов | Математика ЕГЭ для 10 класса | УмскулСкачать

Иррациональные неравенства #1Скачать

Профильный ЕГЭ 2023. Задача 14. Неравенства. Метод интервалов. 10 классСкачать

Иррациональные неравенства #10Скачать

Иррациональные неравенства | Математика ЕГЭ | УмскулСкачать

Иррациональные уравнения и их системы. 11 класс.Скачать

Иррациональные уравнения | Математика ЕГЭ 10 класс | УмскулСкачать

Как решать иррациональные уравнения. Методы решения иррациональных уравнений. (часть 1).Скачать

8 класс, 38 урок, Иррациональные уравненияСкачать

✓ Метод интервалов. Рациональные уравнения и неравенства | Борис ТрушинСкачать

✓ Иррациональное уравнение | ЕГЭ-2018. Задание 12. Математика. Профильный уровень | Борис ТрушинСкачать

Этот АЛГОРИТМ позволит решать неравенства за 1 минуту — Дробно-Рациональные НеравенстваСкачать