Решение интегральных уравнений в физике

п.1. От ускорения к скорости и координате

Рассматривая применение производной в физике и технике (см. §51 данного справочника), мы во второй производной от уравнения прямолинейного равномерного движения (x(t)) пришли к постоянному ускорению (a=const).
С помощью интегрирования можно пройти обратный путь.
Начнем с постоянного ускорения (a=const).
Интеграл от ускорения по времени – это скорость: $$ v(t)=int adt=aint dt=at+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная скорость (v_0). Получаем: $$ v(t)=at+v_0 $$ Интеграл от скорости по времени – это координата: $$ x(t)=int v(t)dt=int (at+v_0)dt=frac+v_0 t+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная координата (x_0). Получаем: $$ x(t)=frac+v_0 t+x_0 $$ Таким образом, если нам известны ускорение (a), начальная скорость (v_0) и начальная координата (x_0), мы всегда сможем получить уравнение движения (x(t)).

п.2. Физические величины как интегралы других величин

Если (v(t)) — скорость некоторого физического процесса, уравнение этого процесса можно найти интегрированием: $$ f(t)=int v(t)dt $$ Такие величины часто встречаются в различных разделах физики и техники.

Скорость (v(t)=int a(t)dt)

Координата (x(t)=int v(t)dt)

Угловое ускорение (beta(t))

Угловая скорость (omega(t)=int beta(t) dt)

Угловая скорость (omega(t))

Угол поворота (varphi(t)=intomega(t)dt)

Скорость расходования горючего (u(t))

Масса горючего ракеты (m(t)=int u(t)dt)

Заряд (q(t)=int I(t)dt)

Работа (A(t)=int N(t)dt)

ЭДС индукции (varepsilon(t))

Магнитный поток (Ф(t)=-intvarepsilon(t)dt)

Скорость радиоактивного распада (I(t))

Число атомов радиоактивного вещества (N(t)=int I(t)dt)

Берутся интегралы и по другим переменным. Например, чтобы найти работу переменной силы (F(x)), нужно взять интеграл по координате: $$ A=int_^F(x)dx $$ В трехмерном пространстве интегралы могут браться по всем трем координатам.
При решении уравнений в частных производных интегралы берутся и по времени и по координатам.

В современной физике интеграл по времени берётся также и от самого уравнение движения. Полученная скалярная величина называется действием и носит фундаментальный характер. В простейшем случае: $$ S_0=int overrightarrow

cdot overrightarrowdt $$ где (overrightarrow

cdot overrightarrow) — скалярное произведение векторов импульса и скорости.

п.3. Примеры

Пример 1. Тело движется со скоростью (v(t)) (м/с). Найдите путь, пройденный за промежуток времени от (t_1) до (t_2) (с):
a) (v(t)=3t+2t^2, t_1=0, t_2=6)
Путь: begin s(t)=int_^v(t)dt\ s=int_^(3t+2t^2)dt=left(frac+fracright)|_^=frac+frac-0=\ =3cdot 18+4cdot 36=54+144=198 text end
б) (v(t)=2(t+2)^, t_1=0, t_2=7) begin s=int_^2(t+2)^dt =2cdotfrac<(t+2)^>|_^=frac47cdot 9^-0=frac47cdot 3^7approx 1250 text end

Пример 2. . Сила тока в проводнике изменяется по закону (I(t)=e^+2t) (время в секундах, ток в амперах). Какой заряд пройдет через поперечное сечение проводника за время от второй до шестой секунды?
Заряд: begin Q(t)=int_^I(t)dt end По условию: begin Q=int_^(e^+2t)dt=(-e^+t^2)|_^=-e^+6^2+e^-2^2=frac-frac+32=\ =frac+32approx 32,1 text end

Пример 3*. Найдите путь, который пройдет тело от начала движения до возвращения в исходную точку, если его скорость (v(t)=18t-9t^2) (время в секундах, скорость в м/с). Движение тела прямолинейное.

Если тело вернулось в исходную точку, оно меняло направление движения.
В момент разворота скорость равна нулю. Решаем уравнение: $$ 18t-9t^2=0Rightarrow 9t(2-t)=0Rightarrow left[ begin t=0\ t=2 end right. $$ (t=0) – начало движения, (t=2) — разворот.

Уравнение движения: $$ x(t)=int(18t-9t^2)dt=9t^2-3t^3+C $$ В начальный момент времени (x_0=0Rightarrow C=0) $$ x(t)=9t^2-3t^3 $$ В точке C(2;12) кривая (x(t)) имеет максимум. Тело двигалось в течение 2 с в одну сторону и прошло 12 м, а затем за 1 с вернулось обратно.

Общий путь: 12+12 = 24 м.

Пример 4*. Найдите работу, которую необходимо совершить, чтобы выкачать воду из полусферического котла радиуса R м.

Найдем работу (dA), которую нужно совершить, чтобы выкачать слой воды толщиной (dH) с глубины (H).
Радиус слоя на глубине (H: r^2=R^2-H^2) — по теореме Пифагора.
Объем слоя воды: (dV=pi r^2 dH=pi(R^2-H^2)dH)
Масса слоя воды: (dm=rho dV=pirho(R^2-H^2)dH)
Работа по подъему слоя на высоту (H): $$ dA=dmcdot gH=pirho gH(R^2-H^2)dH $$ Получаем интеграл: begin A=int_^dA=int_^pirho gH(R^2-H^2)dH=pirho gint_^(HR^2-H^3)dH=\ =pirho gleft(fracR^2-fracright)|_^=pirho gleft(frac-frac-0right)=fracpi 4=rho gR^4 end Ответ: (A=fracpi 4=rho gR^4)

Пример 5*. Какую работу выполняют при запуске ракеты массой m кг с поверхности планеты на высоту h м, если радиус планеты равен R м и масса планеты равна M кг?
Сравните работу при запуске ракеты с Земли и Луны на высоту одного радиуса небесного тела, если ускорение свободного падения на поверхности Луны (g_M=1,62) м/с 2 , радиус Луны (R_M=1737) км; для Земли соответственно (g_E=9,81) м/с 2 (R_E=6371) км.

Ускорение свободного падения на поверхности планеты: (g_0=Gfrac)
Ускорение свободного падения при подъеме на высоту x: begin g(x)=Gfrac end Работа по преодолению силы тяжести (F(x)=mg(x)) при подъеме ракеты на высоту h: begin A=int_^mg(x)dx=mint_^Gfracdx=GmMint_^frac=\ =GmMcdotleft(-fracright)|_^=GmMcdotleft(-frac+frac1Rright)=GmMleft(frac1R-fracright)=\ =GmMfrac=GmMfrac end Также, если выразить работу через ускорение свободного падения на поверхности планеты: $$ A=fracfrac=mg_0frac

---

$$ Работа по запуску на высоту одного радиуса небесного тела (h=R): $$ A(R)=mg_0frac=frac $$ Отношение работ по запуску на один радиус на Земле и Луне: $$ frac=frac=frac, frac=fracapprox 22,2 $$ На Земле работа в 22,2 раза больше.

Решения интегральных уравнений онлайн

В этом разделе мы рассмотрим типовые задачи по интегральным уравнениям с решениями. Интегральное уравнение содержит неизвестную функцию под знаком интеграла (по аналогии как дифференциальное — функцию под знаком дифференциала:)).

Выделяют два основных класса интегральных уравнений: уравнения Фредгольма I и II рода:

$$ (I) quad int_a^b K(x,s)u(s)ds = f(x),\ (II) quad u(x)=int_a^b K(x,s)u(s)ds + f(x). $$

В случае переменного верхнего предела интегрирования получаем соответственно уравнение Вольтерра I и II рода:

$$ (I) quad int_a^x K(x,s)u(s)ds = f(x),\ (II) quad u(x)=int_a^x K(x,s)u(s)ds + f(x). $$

Это линейные неоднородные уравнения (при $f(x)=0$ — однородные), иногда рассматриваются более общий случай с параметром $lambda$ перед интегралом.

Ниже вы найдете примеры нахождения решений интегральных уравнений, собственных значений и функций, исследования ядра, применения интегральных уравнений для решения других задач.

Примеры решений интегральных уравнений

Задача 1. Пользуясь теоремой Гильберта-Шмидта, исследовать и решить интегральное уравнение 2-го рода $(E+lambda A)x=y$ в гильбертовом пространстве $X$.

Задача 2. Найти собственные значения и собственные функции уравнения:

$$ y(x)=lambda int_0^1 (cos 2pi x +2x sin 2pi t +t sin pi x)y(t)dt. $$

Задача 3. Решить уравнение Вольтерры, сведя его к обыкновенному дифференциальному уравнению.

Задача 4. Решить или установить неразрешимость уравнений с вырожденным ядром.

Задача 5. Решить интегральное уравнение, сведя его предварительно к обыкновенному дифференциальному уравнению.

Задача 6. Найти резольвенту для интегрального уравнения Вольтерры со следующим ядром $K(x,t)=x^t^$.

Задача 7. Исследовать решения уравнения с вырожденным ядром при различных значениях параметра $lambda$ (ограничиться случаем вещественных характеристических чисел).

$$ y(x)-lambda int_0^1 x y(t)dt = sin 2pi x. $$

Задача 8. Для симметричного ядра $$K(x,t) = frac sin |x-t| quad (0 le, x,t le pi)$$ найти характеристические числа и соответствующие им собственные функции, сводя интегральное уравнение к однородной краевой задаче для обыкновенного дифференциального уравнения.

Задача 9. Решить краевую задачу, используя функцию Грина

Задача 10. Применяя преобразование Лапласа, решить интегральное уравнение

Помощь с интегральными уравнениями

Если вам нужна помощь с решением задач и контрольных по интегральным уравнениям (и другим разделам математического и функционального анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 200 рублей , оформление производится в Word, срок от 1 дня.

Интегрирование уравнений движения

Симуляция физики делает небольшие предсказания на основании законов физики. Эти предсказания на самом деле достаточно просты, что-то вроде «если объект вот здесь и он движется с такой скоростью в этом направлении, то за краткий промежуток времени он окажется вот тут». Мы создаём такие предсказания с помощью математической техники под названием интегрирование.

Темой этой статьи как раз и будет реализация такого интегрирования.

Интегрирование уравнений движения

Вы можете помнить из курса старшей школы или вуза, что сила равна произведению массы на ускорение.

Преобразуем это уравнение и увидим, что ускорение равно силе, делённой на массу. Это соответствует нашим интуитивным ожиданиям, потому что тяжёлые объекты труднее бросать.

Ускорение — это темп изменения скорости от времени:

Аналогично, скорость — это темп изменения позиции от времени:

Это значит, что если мы знаем текущие позицию и скорость объекта, а также приложенные к нему силы, то сможем проинтегрировать, чтобы найти его позицию и скорость в определённый момент времени.

Численное интегрирование

Если вы не изучали дифференциальные уравнения в вузе, то можете вздохнуть спокойно — вы почти в такой же ситуации, что и те, кто их изучал, потому что мы не будем решать дифференциальные уравнения аналитически. Вместо этого мы будем искать решение численным интегрированием.

Вот как работает численное интегрирование: во-первых, начнём с исходной позиции и скорости, затем сделаем небольшой шаг вперёд, чтобы найти скорость и позицию в будущем. Затем повторим это, двигаясь вперёд небольшими шагами, используя результат предыдущих вычислений как исходную точку следующих.

Но как нам найти изменение скорости и позиции на каждом шаге?

Ответ лежит в уравнениях движения.

Давайте назовём наше текущее время t, а шаг времени dt или «delta time».

Теперь мы можем представить уравнения движения в понятном всем виде:

Интуитивно это понятно: если вы находитесь в автомобиле, движущемся со скоростью 60 км/ч, то за один час вы проедете 60 км. Аналогично, автомобиль, ускоряющийся на 10 км/ч в секунду, через 10 секунд будет двигаться на 100 км/ч быстрее.

Разумеется, эта логика сохраняется, только когда ускорение и скорость постоянны. Но даже если они меняются, то это для начала вполне неплохая аппроксимация.

Давайте представим это в коде. Начнём с стационарного объекта массой один килограмм и приложим к нему постоянную силу в 10 кН (килоньютонов) и сделаем шаг вперёд, принимая, что один временной шаг равен одной секунде:

Вот каким будет результат:

Как вы видите, на каждом шаге мы знаем и позицию, и скорость объекта. Это и есть численное интегрирование.

Явный метод Эйлера

Вид интегрирования, который мы только что использовали, называется явным методом Эйлера.

Он назван в честь швейцарского математика Леонарда Эйлера, впервые открывшего эту технику.

Интегрирование Эйлера — это простейшая техника численного интегрирования. Она точна на 100% только когда темп изменений в течение шага времени постоянен.

Поскольку в примере выше ускорение постоянно, интегрирование скорости выполняется без ошибок. Однако мы ещё интегрируем и скорость для получения позиции, а скорость увеличивается из-за ускорения. Это значит, что в проинтегрированной позиции возникает ошибка.

Но насколько велика эта ошибка? Давайте выясним!

Существует аналитическое решение движения объекта при постоянном ускорении. Мы можем использовать его, чтобы сравнить численно интегрированную позицию с точным результатом:

Через 10 секунд объект должен был переместиться на 500 метров, но явным метод Эйлера даёт нам результат 450. То есть погрешность в целых 50 метров всего за 10 секунд!

Кажется, что это невероятно плохо, но в играх обычно для шага физики берётся не такой большой временной интервал. На самом деле, физика обычно вычисляется с частотой, примерно равной частоте кадров дисплея.

Если задать шаг dt = 1 ⁄₁₀₀, то мы получим гораздо лучший результат:

Как вы видите, это достаточно хороший результат, определённо вполне достаточный для игры.

Почему явный метод Эйлера не (всегда) так уж хорош

С достаточно малым шагом времени явный метод Эйлера при постоянном ускорении даёт вполне достойные результаты, но что будет, если ускорение не постоянно?

Хорошим примером переменного ускорения является система пружинного амортизатора.

В этой системе масса присоединена к пружине, и её движение гасится чем-то вроде трения. Существует сила, пропорциональная расстоянию до объекта, которая притягивает его к исходной точке, и сила, пропорциональная скорости объекта, но направленная в противоположном направлении, которая замедляет его.

Здесь ускорение в течение шага времени совершенно точно изменяется, но эта постоянно меняющаяся функция является сочетанием позиции и скорости, которые сами постоянно изменяются за шаг времени.

Вот пример гармонического осциллятора с затуханием. Это хорошо изученная задача, и для него существует аналитическое решение, которое можно использовать для проверки результата численного интегрирования.

Давайте начнём со слабозатухающей системы, в которой масса колеблется рядом с исходной точкой, постепенно замедляясь.

Вот входные параметры системы масса-пружина:

• Масса: 1 килограмм
• Исходная позиция: 1000 метров от исходной точки
• Коэффициент упругости по закону Гука: k = 15
• Коэффициент затухания по закону Гука: b = 0.1

И вот график точного решения:

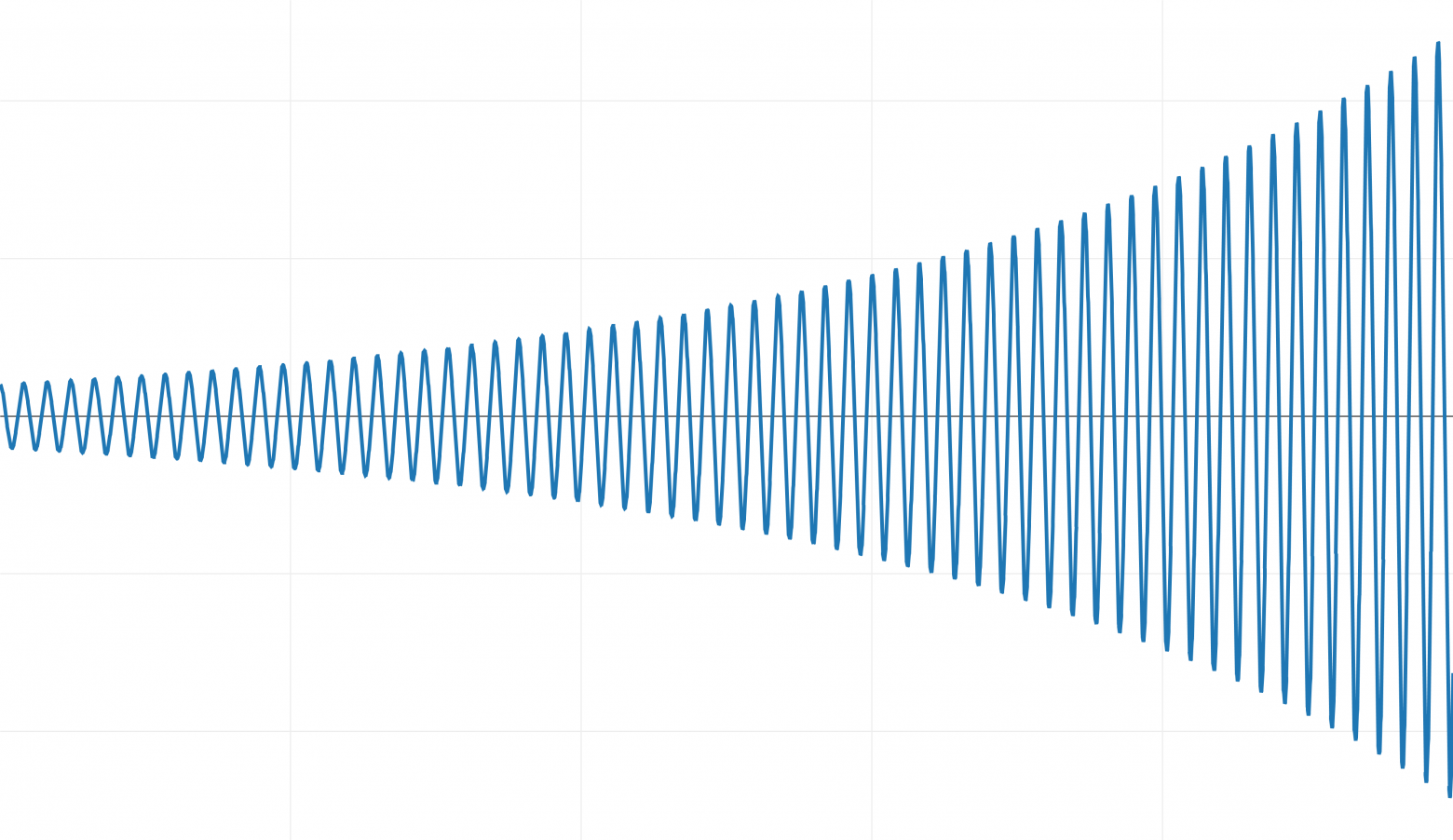
Если для интегрирования этой системы мы применим явный метод Эйлера, то получим следующий результа, который я отмасштабировал по вертикали:

Вместо затухания и сближения с исходной точкой, система со временем набирает энергию!

При интегрировании явным методом Эйлера и с dt= 1 ⁄₁₀₀ такая система нестабильна.

К сожалению, поскольку мы уже интегрируем с малым шагом времени, то не имеем практичных способов повышения точности. Даже если мы уменьшим шаг времени, то всегда будет коэффициент упругости k, при котором мы получим такое поведение.

Симплектический метод Эйлера

Мы можем рассмотреть ещё один интегратор — симплектический метод Эйлера.

В большинстве коммерческих игровых физических движков используется этот интегратор.

Переход от явного к симплектическому методу Эйлера заключается только в замене:

Использование симплектического интегратора Эйлера при dt = 1 ⁄₁₀₀ для системы пружинного амортизатора даёт стабильный результат, очень близкий к точному решению:

Даже несмотря на то, что симплектический метод Эйлера имеет ту же степень точности, что и явный метод (степень 1), при интегрировании уравнений движения мы получаем намного лучший результат, потому что оно является симплектическим.

Существует множество других методов интегрирования

И теперь нечто совершенно другое.

Неявный метод Эйлера — это способ интегрирования, хорошо подходящий для интегрирования жёстких уравнений, которые при других методах становятся нестабильными. Его недостаток заключается в том, что он требует решения системы уравнений на каждом шаге времени.

Интегрирование Верле обеспечивает бо́льшую точность, чем неявный метод Эйлера, и требует меньше памяти при симуляции большого числа частиц. Это интегратор второй степени, который тоже является симплектическим.

Существует целое семейство интеграторов, называемое методами Рунге-Кутты. На самом деле, явный метод Эйлера считается частью этого семейства, но в него входят интеграторы и более высокого порядка, самым классическим из которых является метод Рунге-Кутты порядка 4 (Runge Kutta order 4) или просто RK4.

Это семейство интеграторов названо в честь открывших их немецких физиков: Карла Рунге и Мартина Кутты.

RK4 — это интегратор четвёртого порядка, то есть накапливаемая ошибка имеет порядок четвёртой производной. Это делает метод очень точным, гораздо более точным, чем явный и неявный методы Эйлера, имеющие только первый порядок.

Но хотя он более точен, нельзя сказать, что RK4 автоматически становится «лучшим» интегратором, или даже что он лучше симплектического метода Эйлера. Всё гораздо сложнее. Тем не менее, это довольно интересный интегратор и его стоит изучить.

Реализация RK4

Существует уже много объяснений математики, используемой в RK4. Например: здесь, здесь и здесь. Я настоятельно рекомендую изучить его выведение и понять, как и почему он работает на математическом уровне. Но я понимаю, что целевая аудитория этой статьи — программисты, а не математики, поэтому мы здесь будем рассматривать только реализацию. Так что давайте приступим.

Прежде чем приступить, давайте зададим состояние объекта как struct в C++, чтобы можно было удобно хранить позицию и скорость в одном месте:

Также нам нужна структура для хранения производных значений состояний:

Теперь нам нужна функция для вычисления состояния физики из t в t+dt с помощью одного набора производных, а после этого для вычисления производных в новом состоянии:

Функция ускорения управляет всей симуляцией. Давайте используем её в системе пружинного амортизатора и вернём ускорение для единичной массы:

То, что нужно здесь записать, разумеется, зависит от симуляции, но необходимо структурировать симуляцию таким образом, чтобы можно было вычислять ускорение внутри этого метода для заданных состояния и времени, в противном случае он не подойдёт для интегратора RK4.

Наконец, мы получаем саму процедуру интегрирования:

Интегратор RK4 делает выборку производной в четырёх точках, чтобы определить кривизну. Заметьте, как производная a используется при вычислении b, b используется при вычислении c, и c для d. Эта передача текущей производной в вычисление следующей и даёт интегратору RK4 его точность.

Важно то, что каждая из этих производных a, b, c и d будет разной, когда темп изменения в этих величинах является функцией времени или функцией самого состояния. Например, в нашей системе пружинного амортизатора ускорение является функцией текущей позиции и скорости, которые меняются в шаге времени.

После вычисления четырёх производных наилучшая общая производная вычисляется как взвешенная сумма, полученная из разложения в ряд Тейлора. Эта комбинированная производная используется для перемещения позиции и скорости вперёд во времени, точно так же, как мы делали это в явном интеграторе Эйлера.

Сравнение симплектического метода Эйлера и RK4

Давайте подвергнем проверке интегратор RK4.

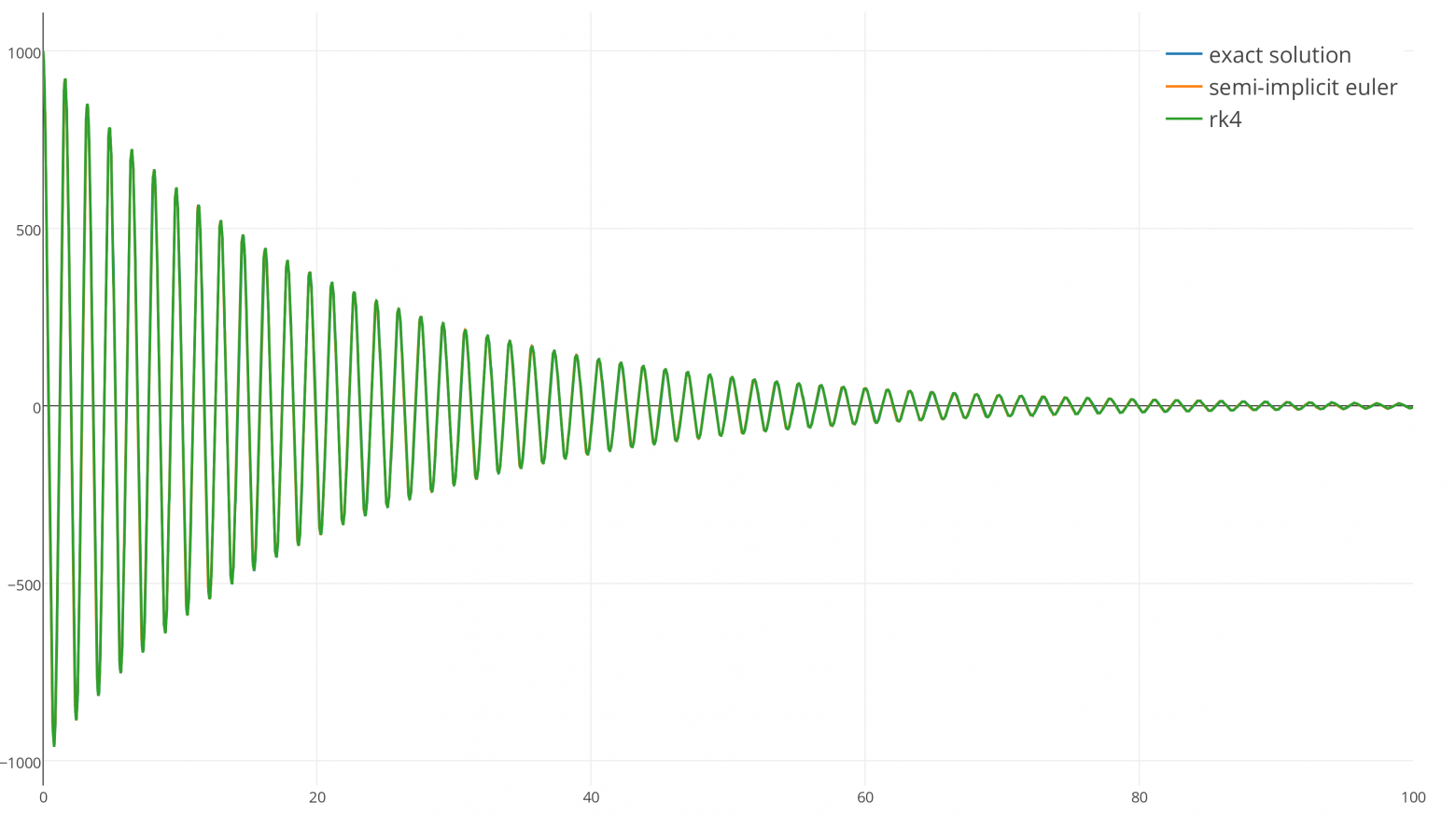
Очевидно, что поскольку он является интегратором более высокого порядка (четвёртый против первого) он наглядно будет более точен, чем симплектический метод Эйлера, правда?

Неправда. Оба интегратора так близки к точному результату, что при таком масштабе почти невозможно найти между ними разницу. Оба интегратора стабильны и очень хорошо повторяют точное решение при dt= 1 ⁄₁₀₀.

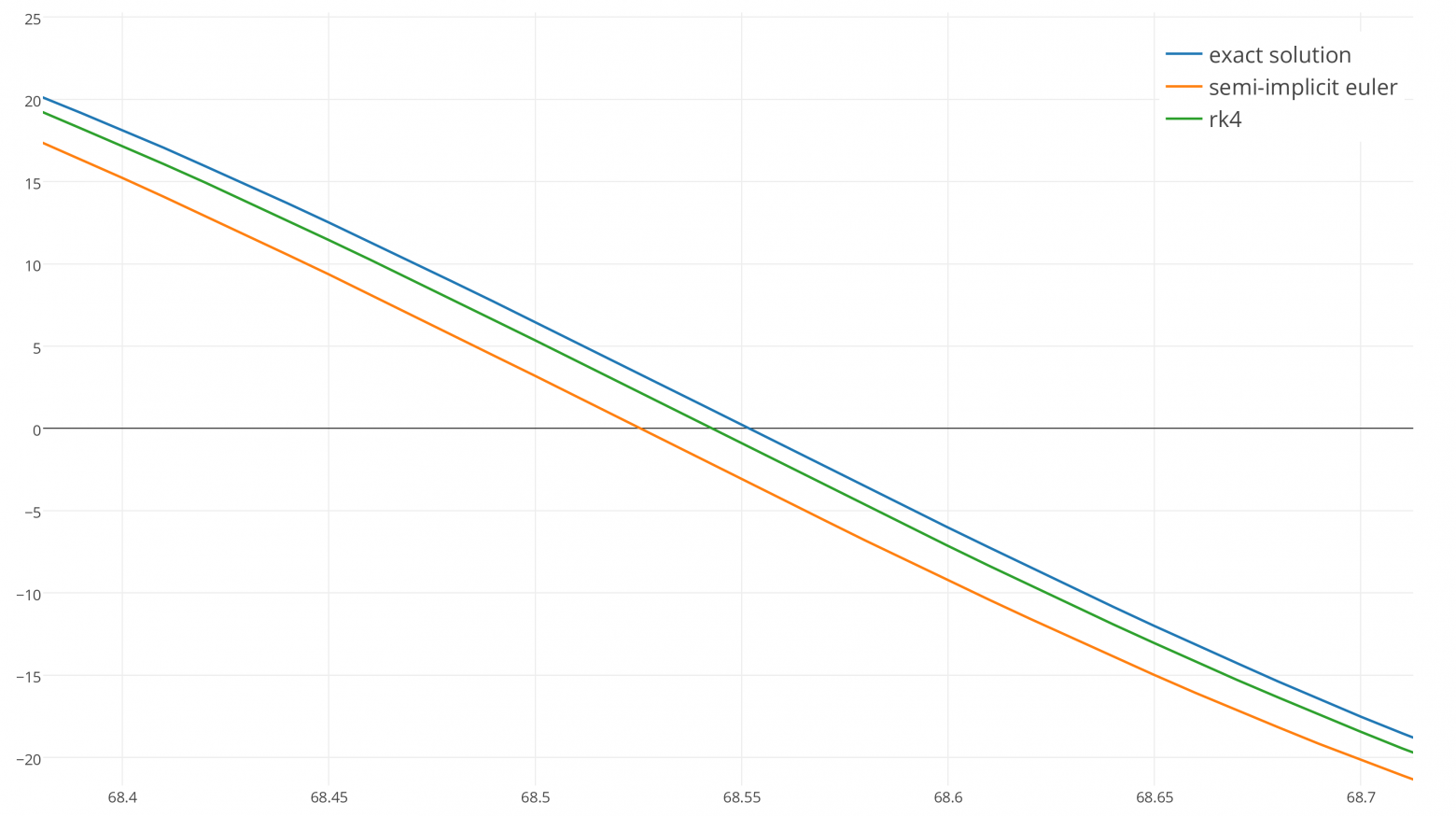
При увеличении видно, что RK4 действительно более точен, чем симплектический метод Эйлера, но стоит ли эта точность сложности и лишнего времени выполнения RK4? Трудно судить.

Давайте постараемся и посмотрим, сможем ли мы найти значительное различие между двумя интеграторами. К сожалению, мы не сможем долго наблюдать за этой системой, потому что она быстро затухает до нуля, поэтому давайте перейдём к простому гармоническому осциллятору, который колеблется бесконечно и без затуханий.

Вот точный результат, к которому мы будем стремиться:

Чтобы усложнить интеграторам задачу, давайте увеличим шаг времени до 0,1 секунды.

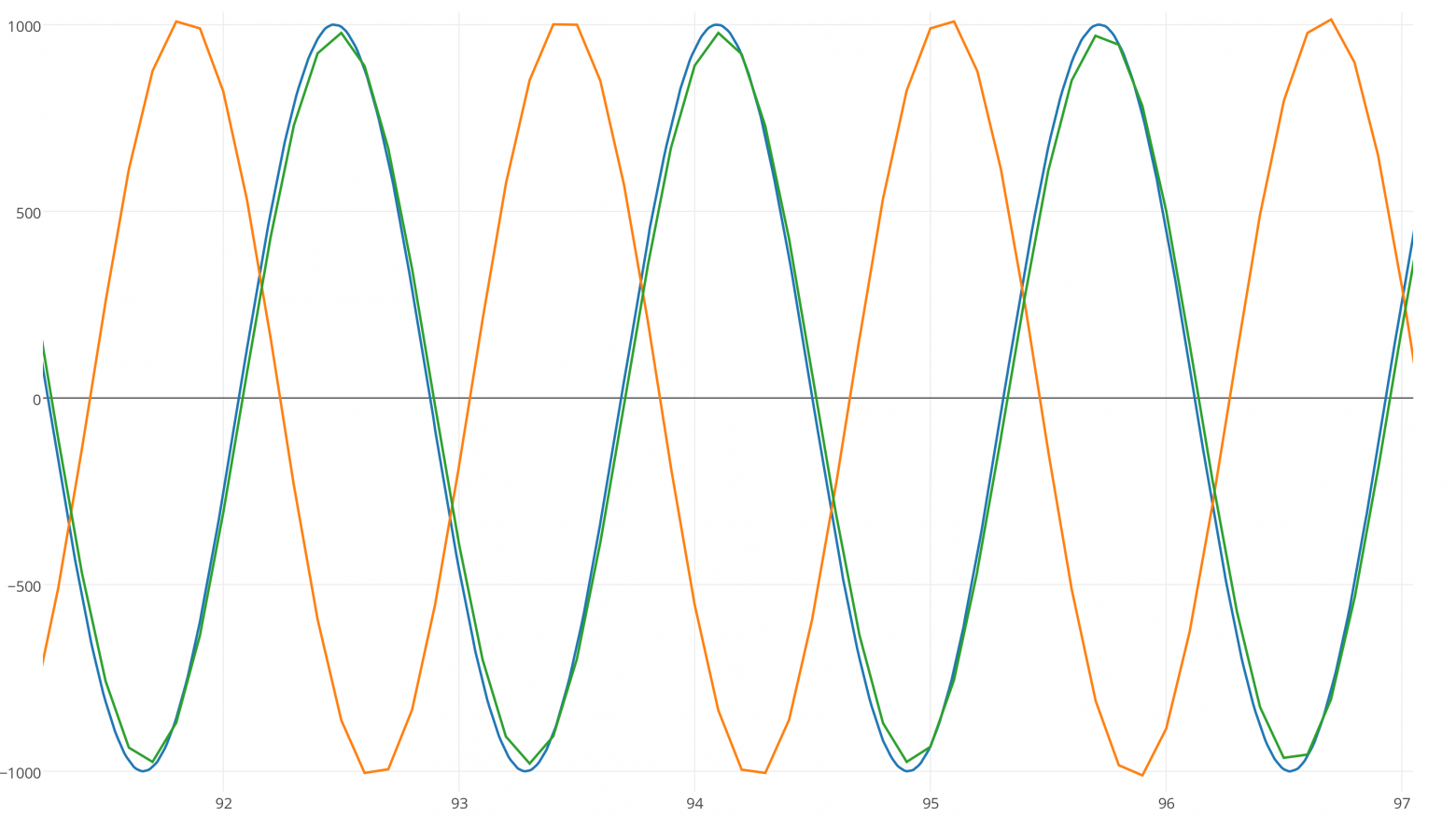
Теперь запустим интеграторы на 90 секунд и увеличим масштаб:

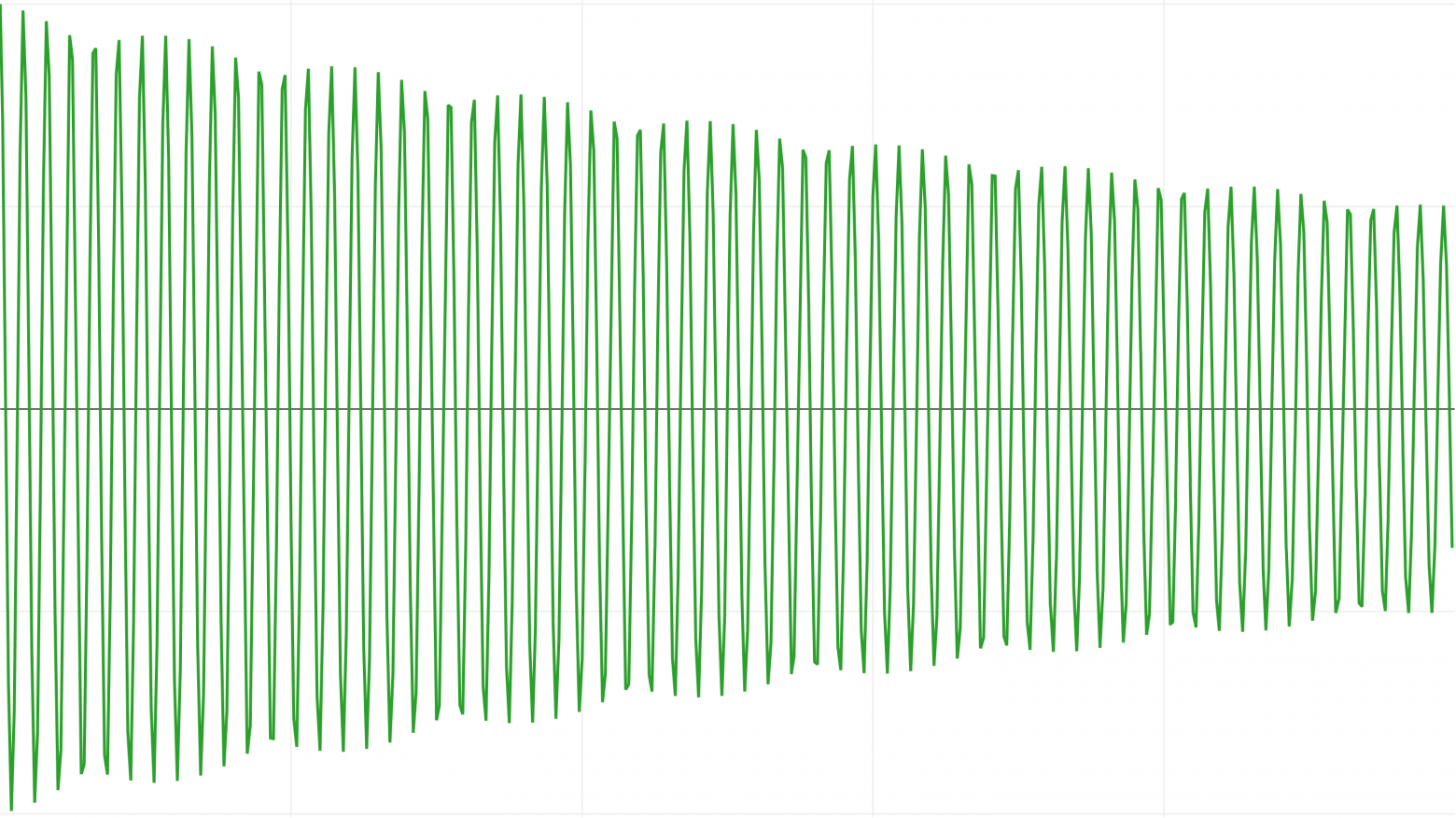
Через 90 секунд симплектический метод Эйлера (оранжевая кривая) сдвинулся по фазе относительно точного решения, потому что его частота немного отличалась, в то время как зелёная кривая RK4 соответствует частоте, но теряет энергию!

Мы чётко можем это заметить, увеличив шаг времени до 0,25 секунды.

RK4 сохраняет верную частоту, но теряет энергию:

А симплектический метод Эйлера в среднем намного лучше сохраняет энергию:

Но от сдвигается от фазы. Какой интересный результат! Как вы видите, если RK4 имеет более высокий порядок точности, то он не обязательно «лучше». В этом вопросе есть множество нюансов.

Заключение

Мы реализовали три различных интегратора и сравнили результаты.

1. Явный метод Эйлера
2. Симплектический метод Эйлера
3. Метод Рунге-Кутты порядка 4 (RK4)

Так какой же интегратор стоит использовать в игре?

Я рекомендую симплектический метод Эйлера. Он «дёшев» и прост в реализации, гораздо стабильнее явного метода Эйлера и в среднем стремится к сохранению энергии даже при близких к предельным условиях.

Если вам действительно нужна бОльшая точность, чем у симплектического метода Эйлера, я рекомендую посмотреть на симплектические интеграторы более высокого порядка, рассчитанные на гамильтоновы системы. Таким образом вы изучите более современные техники интегрирования высокого порядка, которые лучше подходят для симуляций, чем RK4.

И наконец, если вы всё ещё пишете в игре такое:

То потратьте секунду и замените эти строки на:

📽️ Видео