- Формула интегрирования по частям
- Примеры интегралов, содержащих логарифм и обратные тригонометрические функции
- Простой пример с логарифмом
- Пример логарифма в степени 2
- Пример, в котором аргумент логарифма является многочленом
- Пример с арксинусом
- Пример с арктангенсом
- Еще один пример с арксинусом
- Решение задач по математике онлайн
- Калькулятор онлайн. Решение логарифмических уравнений.
- Немного теории.
- Логарифмическая функция. Логарифмы
- Свойства логарифмов
- Десятичные и натуральные логарифмы
- Логарифмическая функция, её свойства и график
- Логарифмические уравнения
- Решение логарифмических уравнений
- 🎥 Видео
Видео:Логарифмы в ЕГЭ🫢 Решишь второй?!Скачать

Формула интегрирования по частям
Ниже, при решении примеров, применяется формула интегрирования по частям:
;
.
Подробнее >>>
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Примеры интегралов, содержащих логарифм и обратные тригонометрические функции
Вот примеры интегралов, которые интегрируются по частям:
, , , , , , .
При интегрировании ту часть подынтегрального выражения, которая содержит логарифм или обратные тригонометрические функции обозначают через u , остальное – через dv .
Ниже приведены примеры с подробными решениями этих интегралов.
Простой пример с логарифмом
Вычислим интеграл, содержащий произведение многочлена и логарифма:
Здесь подынтегральное выражение содержит логарифм. Делаем подстановки
u = ln x , dv = x 2 dx . Тогда
,
.
Интегрируем по частям.
.
Вычисляем оставшийся интеграл:
.
Тогда
.
В конце вычислений добавим постоянную C .
Пример логарифма в степени 2
Рассмотрим пример, в котором в подынтегральное выражение входит логарифм в целочисленной степени. Такие интегралы также могут интегрироваться по частям.
Делаем подстановки
u = (ln x ) 2 , dv = x dx . Тогда
,
.
Оставшийся интеграл также вычисляем по частям:
.
Подставляем
.
Пример, в котором аргумент логарифма является многочленом
По частям могут вычисляться интегралы, в подынтегральное выражение которого входит логарифм, аргумент которого является многочленом, рациональной или иррациональной функцией. В качестве примера, вычислим интеграл с логарифмом, аргумент которого является многочленом.
.
Делаем подстановки
u = ln( x 2 – 1) , dv = x dx .
Тогда
,
.
Вычисляем оставшийся интеграл:
.
Мы здесь не пишем знак модуля ln | x 2 – 1| , поскольку подынтегральное выражение определено при x 2 – 1 > 0 . Подставляем
.
Пример с арксинусом
Рассмотрим пример интеграла, в подынтегральное выражение которого входит арксинус.
.
Делаем подстановки
u = arcsin x ,
.
Тогда
,
.
Далее замечаем, что подынтегральное выражение определено при |x| 1 . Раскроем знак модуля под логарифмом, учитывая что 1 – x > 0 и 1 + x > 0 .
Пример с арктангенсом
Решим пример с арктангенсом:
.
Интегрируем по частям.
.
Выделим целую часть дроби:
x 8 = x 8 + x 6 – x 6 – x 4 + x 4 + x 2 – x 2 – 1 + 1 = ( x 2 + 1)( x 6 – x 4 + x 2 – 1) + 1 ;
.
Интегрируем:
.
Окончательно имеем:
.
Еще один пример с арксинусом
Интегрируем по частям.
.
Вычисляем оставшийся интеграл. При x > 0 имеем:
.
.
.
При x сделаем подстановку x = – t, t > 0 :
.
Автор: Олег Одинцов . Опубликовано: 19-10-2014
Видео:Проще простого! Как решить Логарифмическое Уравнение?Скачать

Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Видео:Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать

Калькулятор онлайн.
Решение логарифмических уравнений.
Этот математический калькулятор онлайн поможет вам решить логарифмическое уравнение. Программа для решения логарифмического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> ln(b) или log(b) или log(e,b) — натуральный логарифм числа b
log(10,b) — десятичный логарифм числа b
log(a,b) — логарифм b по основанию a
Введите логарифмическое уравнение
Решить уравнение
Видео:✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать

Немного теории.
Видео:Решение логарифмических уравнений. Вебинар | МатематикаСкачать

Логарифмическая функция. Логарифмы
Задача 1. Найти положительный корень уравнения x 4 = 81
По определению арифметического корня имеем ( x = sqrt[4] = 3 )
Задача 2. Решить уравнение 3 x = 81
Запишем данное уравнение так: 3 x = 3 4 , откуда x = 4
В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени. Способ решения задачи 2 состоял в том, что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 3. Но уже, например, уравнение 3 x = 80 таким способом решить не удаётся. Однако это уравнение имеет корень. Чтобы уметь решать такие уравнения, вводится понятие логарифма числа.
Уравнение a x = b, где a > 0, ( a neq 1 ), b > 0, имеет единственный корень. Этот корень называют логарифмом числа b no основанию a и обозначают logab
Например, корнем уравнения 3 x = 81 является число 4, т.е. log381 = 4.
Определение. Логарифмом положительного числа b по основанию a, где a > 0, ( a neq 1 ), называется показатель степени, в которую надо возвести число a, чтобы получить b
log77 = 1, так как 7 1 = 7
Определение логарифма можно записать так:
Действие нахождения логарифма числа называют логарифмированием.
Действие нахождения числа по его логарифму называют потенцированием.
Вычислить log64128
Обозначим log64128 = х. По определению логарифма 64 x = 128. Так как 64 = 2 6 , 128 = 2 7 , то 2 6x = 2 7 , откуда 6x = 7, х = 7/6.
Ответ log64128 = 7/6
Вычислить ( 3^ )
Используя свойства степени и основное логарифмическое тождество, находим
Решить уравнение log3(1-x) = 2
По определению логарифма 3 2 = 1 — x, откуда x = -8
Видео:ЕГЭ база #7 / Логарифмические уравнения / Свойства, определение логарифма / решу егэСкачать

Свойства логарифмов
При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.
Пусть а > 0, ( a neq 1 ), b > 0, c > 0, r — любое действительное число. Тогда справедливы формулы:
Видео:Интересная задача на логарифмы в ЕГЭСкачать

Десятичные и натуральные логарифмы
Для логарифмов чисел составлены специальные таблицы (таблицы логарифмов). Логарифмы вычисляют также с помощью микрокалькулятора. И в том и в другом случае находятся только десятичные или натуральные логарифмы.
Определение. Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут
lg b вместо log10b
Определение. Натуральным логарифмом числа называют логарифм этого числа по основанию e, где e — иррациональное число, приближённо равное 2,7. При этом пишут ln b вместо logeb
Иррациональное число e играет важную роль в математике и её приложениях. Число e можно представить как сумму:
$$ e = 1 + frac + frac + frac + dots + frac + dots $$
Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить логарифмы чисел по любому основанию.
Для этого используется формула замены основания логарифма:
Следствия из формулы замены основания логарифма.
При c = 10 и c = e получаются формулы перехода к десятичным и натуральным логарифмам:
$$ log_a b = frac , ;; log_a b = frac $$
Видео:Логарифмическое уравнение / Как решить?Скачать

Логарифмическая функция, её свойства и график
В математике и её приложениях часто встречается логарифмическая функция
y = logax
где а — заданное число, a > 0, ( a neq 1 )
Логарифмическая функция обладает свойствами:
1) Область определения логарифмической функции — множество всех положительных чисел.
2) Множество значений логарифмической функции — множество всех действительных чисел.
3) Логарифмическая функция не является ограниченной.
4) Логарифмическая функция y = logax является возрастающей на промежутке ( (0; +infty) ), если a > 1,
и убывающей, если 0 1, то функция y = logax принимает положительные значения при х > 1,
отрицательные при 0 1.
Ось Oy является вертикальной асимптотой графика функции y = logax

Отметим, что график любой логарифмической функции y = logax проходит через точку (1; 0).
При решении уравнений часто используется следующая теорема:
Логарифмическая функция y = logax и показательная функция y = a x , где a > 0, ( a neq 1 ), взаимно обратны.
Видео:Логарифмические уравнения. 11 класс.Скачать

Логарифмические уравнения
Решить уравнение log2(x+1) + log2(x+3) = 3
Предположим, что х — такое число, при котором равенство является верным, т.е. х — корень уравнения. Тогда по свойству логарифма верно равенство
log2((x+1)(x+3)) = 3
Из этого равенства по определению логарифма получаем
(x+1)(x+3) = 8
х 2 + 4х + 3 = 8, т.е. х 2 + 4x — 5 = 0, откуда x1 = 1, х2 = -5
Так как квадратное уравнение является следствием исходного уравнения, то необходима проверка.
Проверим, являются ли числа 1 и -5 корнями исходного уравнения.
Подставляя в левую часть исходного уравнения х = 1, получаем
log2(1+1) + log2(1+3) = log22 + log24 = 1 + 2 = 3, т.е. х = 1 — корень уравнения.
При х = -5 числа х + 1 и х + 3 отрицательны, и поэтому левая часть уравнения не имеет смысла, т.е. х = -5 не является корнем этого уравнения.
Ответ x = 1
Решить уравнение lg(2x 2 — 4x + 12) = lg x + lg(x+3)
По свойству логарифмов
lg(2x 2 — 4x + 12) = lg(x 2 + 3x)
откуда
2x 2 — 4x + 12 = x 2 + 3x
x 2 — 7x + 12 = 0
x1 = 3, х2 = 4
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x1 = 3, х2 = 4
Решить уравнение log4(2x — 1) • log4x = 2 log4(2x — 1)
Преобразуем данное уравнение:
log4(2x — 1) • log4x — 2 log4(2x — 1) = 0
log4(2х — 1) • (log4 x — 2) = 0
Приравнивая каждый из множителей левой части уравнения к нулю, получаем:
1) log4 (2х — 1) = 0, откуда 2х — 1 = 1, х1 = 1
2) log4 х — 2 = 0, откуда log4 = 2, х2 = 16
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x1 = 1, х2 = 16
Видео:Умножаем логарифмы В УМЕ🧠Скачать

Решение логарифмических уравнений
Данный калькулятор позволяет найти решение логарифмических уравнений.
Логарифмическое уравнение – это уравнения, в которых переменная величина находится под знаком логарифма. Логарифмическая функция всегда монотонна и может принимать любые значения. Кроме того, переменный аргумент логарифма должен быть больше нуля и переменное основание логарифма должно быть положительным и не равным единице.
При решении логарифмических уравнений зачастую необходимо логарифмировать или потенцировать обе части уравнения. Логарифмировать алгебраическое выражение — выразить его логарифм через логарифмы отдельных чисел, входящих в это выражение. Потенцирование – нахождение выражения, от которого получен результат логарифмирования.
Для того чтобы найти корни логарифмического уравнения, нужно ввести это уравнение в ячейку и нажать на кнопку «Вычислить». В ответе отображаются корни уравнения и график логарифмической функции.
Калькулятор поможет найти решение логарифмических уравнений онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.
| Основные функции |
: x^a
🎥 Видео
11 класс, 17 урок, Логарифмические уравненияСкачать

Логарифмы с Нуля, Что Такое Логарифм? + ДЗ (ЕГЭ 2024 Математика Профиль и База, 10 и 11 класс)Скачать

Логарифмические уравнения и их системы. Практическая часть. 11 класс.Скачать

84 людей этого не знают! Секретный способ решения Логарифмических УравненийСкачать

Преобразование логарифмических выраженийСкачать

КАК СЧИТАТЬ ЛОГАРИФМЫ? #егэматематика2022 #егэ2022 #логарифмы #математика #егэ #огэ #shortsСкачать

§15 ЛогарифмыСкачать

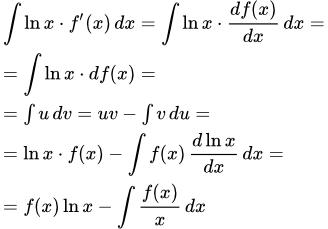


 : x^a
: x^a