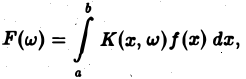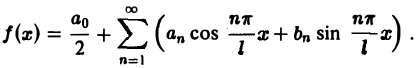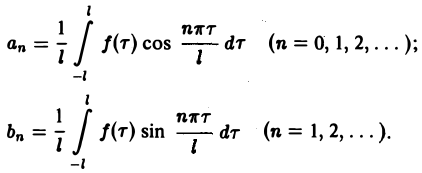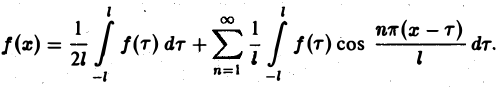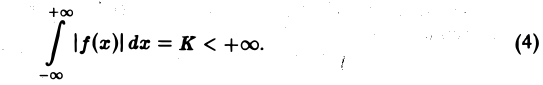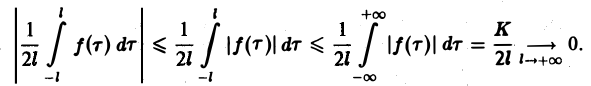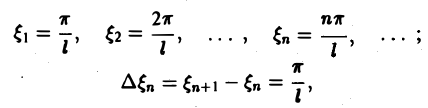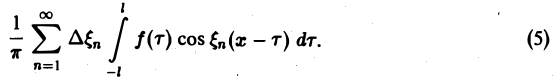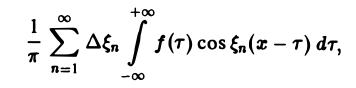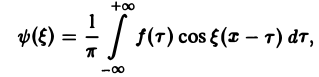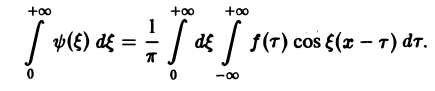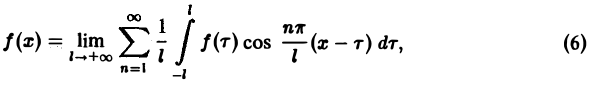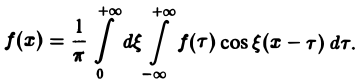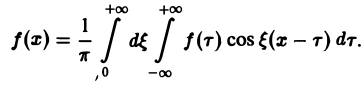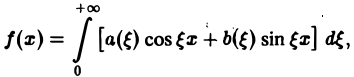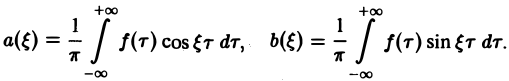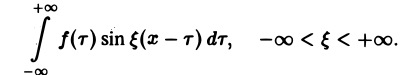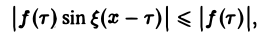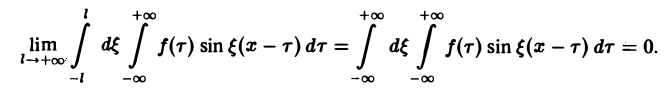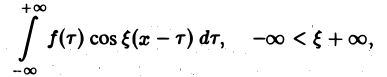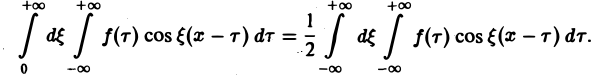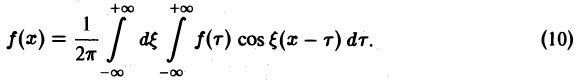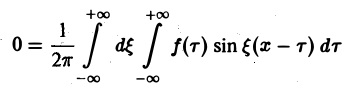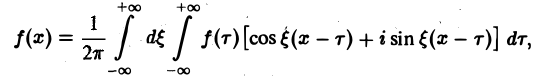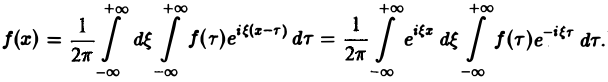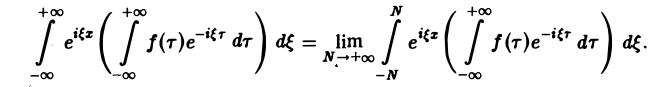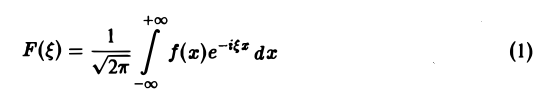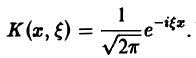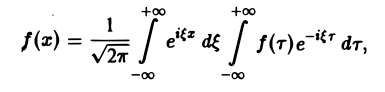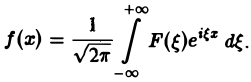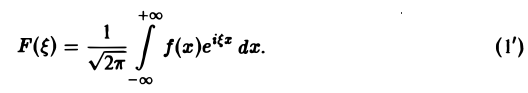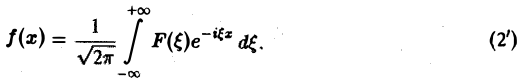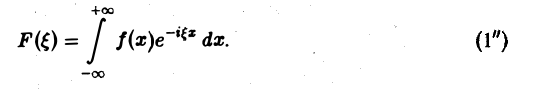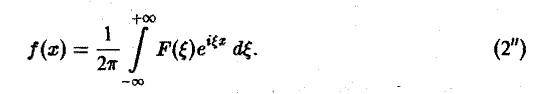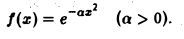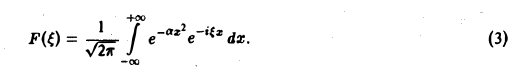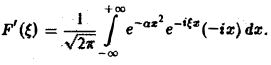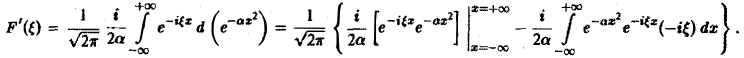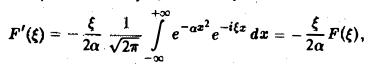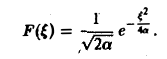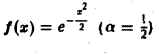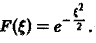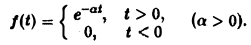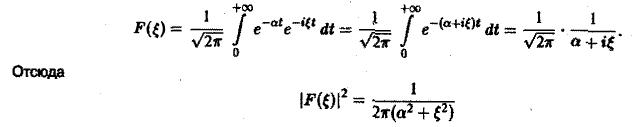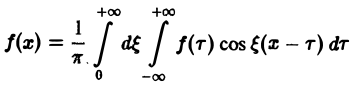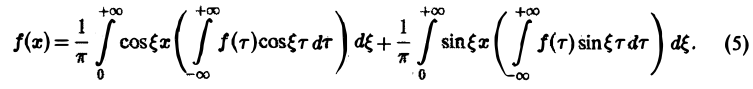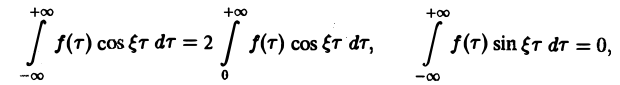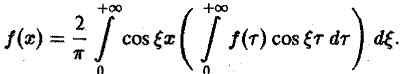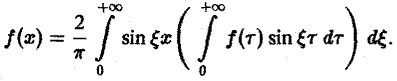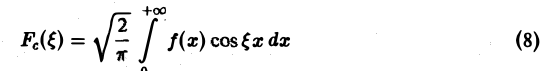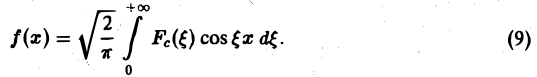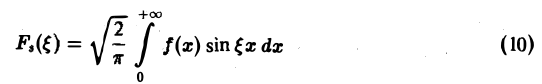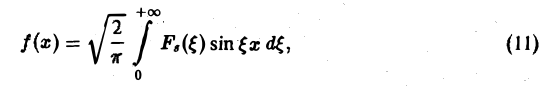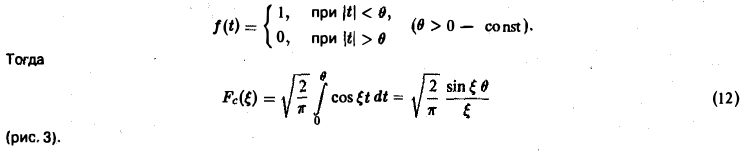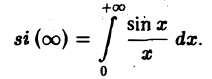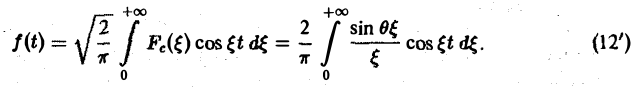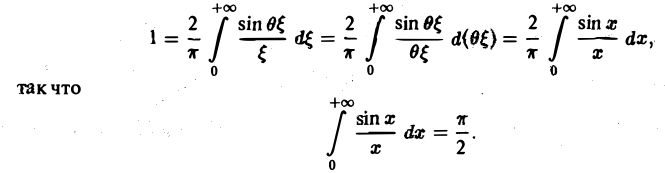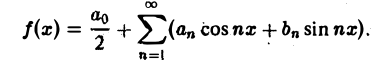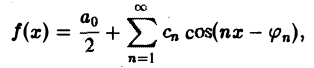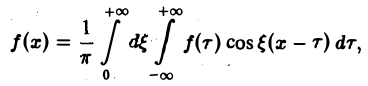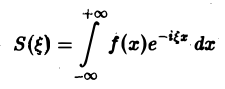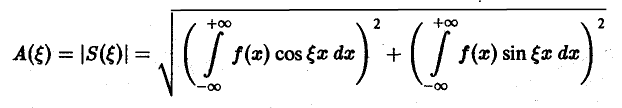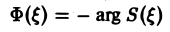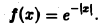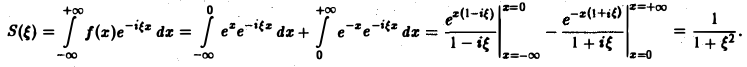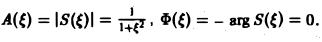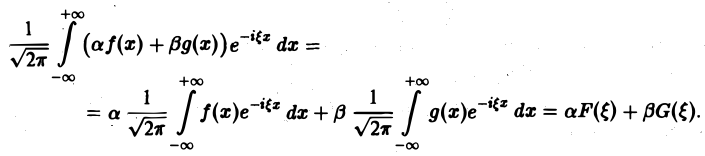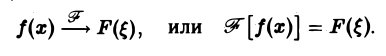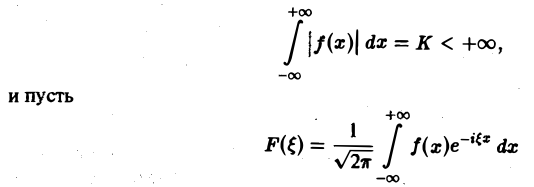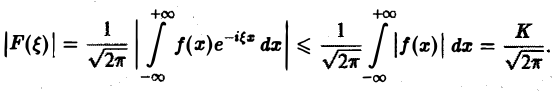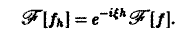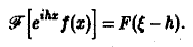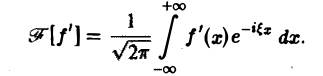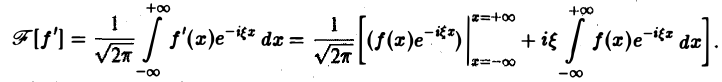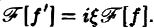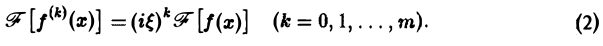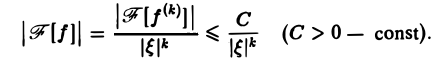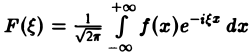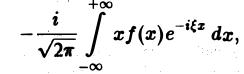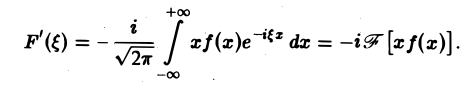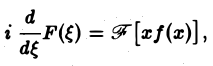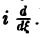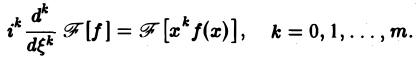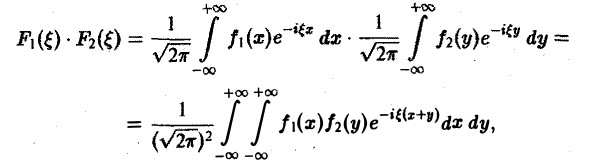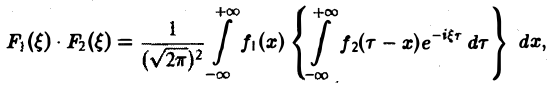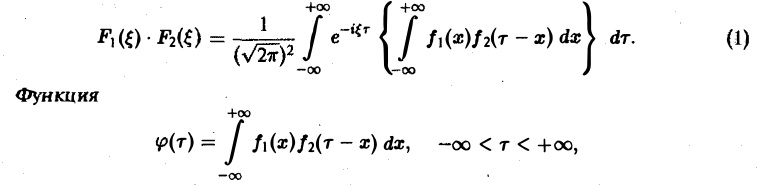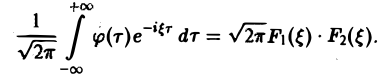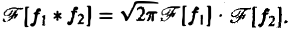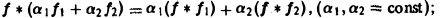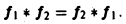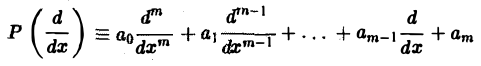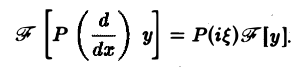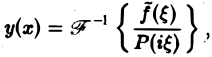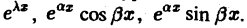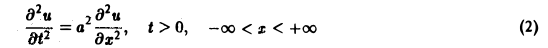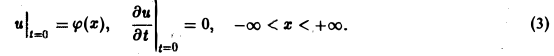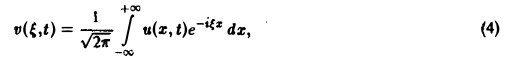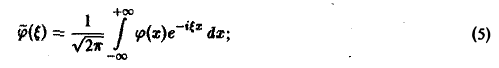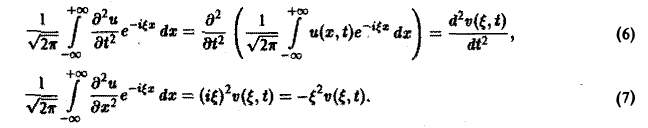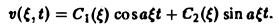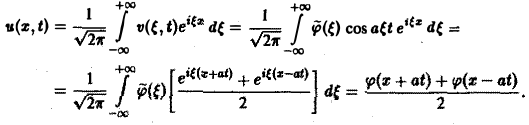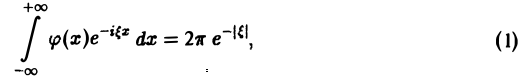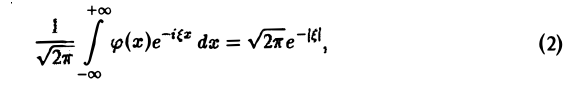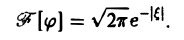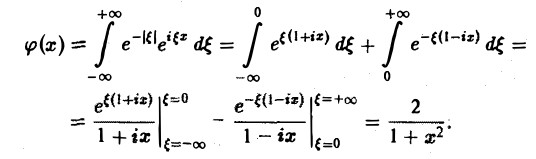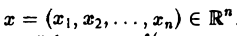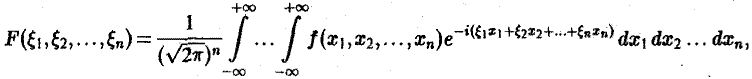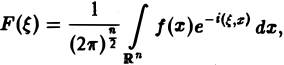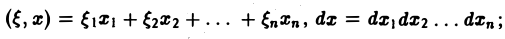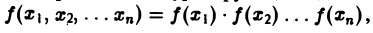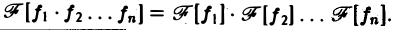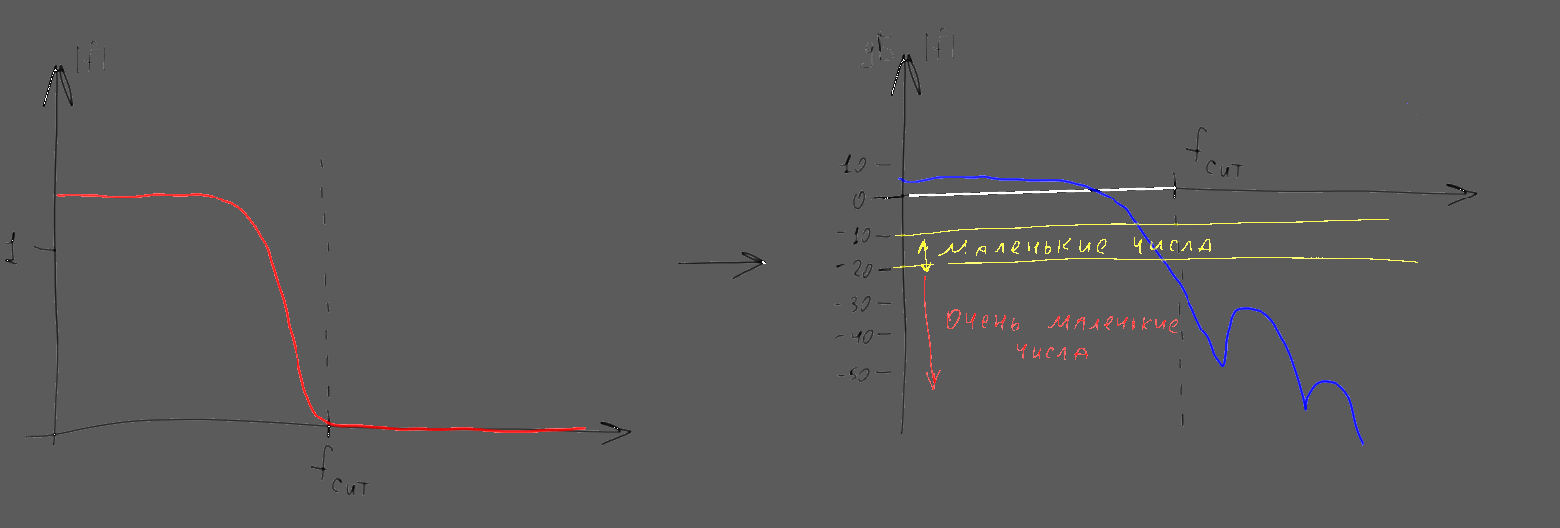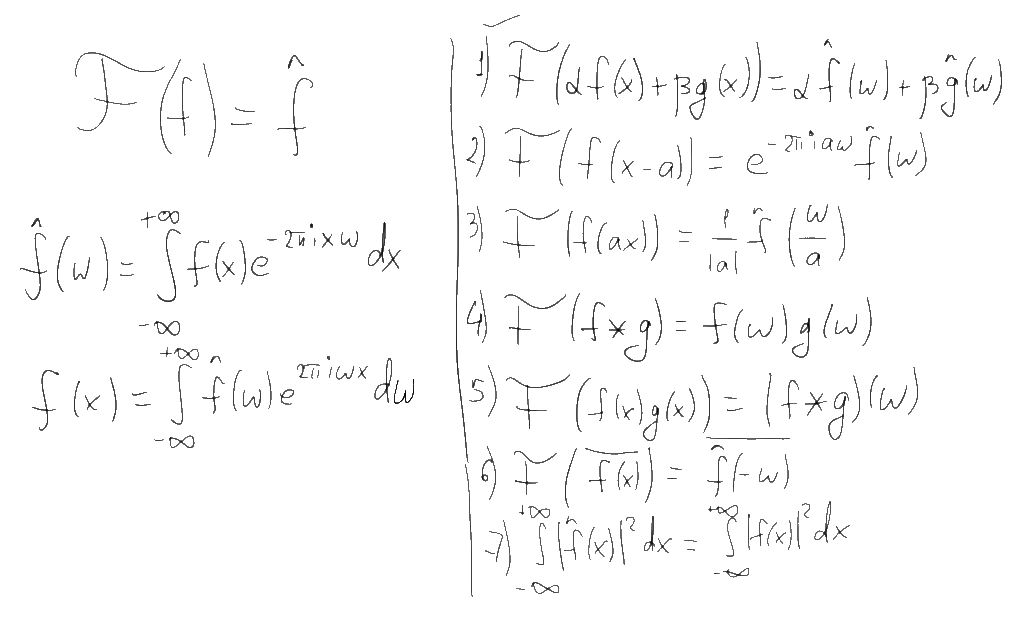Решение интегральных уравнений преобразованием фурье

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

исследования задач математической физики является метод интегральных преобразований. Пусть функция f(x) задана на интервале (а, 6), конечном или бесконечном. Интегральным преобразованием функции f(x) называется функция где К(х, ш) — фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существуете собственном или несобственном смысле). §1.

Интеграл Фурье Всякая функция f(x), которая на отрезке [-f, I] удовлетворяет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом Коэффициенты а*, и 6„ ряда (1) определяются по формулам Эйлера—Фурье: ПРЕОБРАЗОВАНИЕ ФУРЬЕ Интеграл Фурье Комплексная форма интеграла Преобразование Фурье Косинус и синус преобразования Амплитудный и фазовый спектры Свойства Приложения Ряд в правой части равенства (1) можно записать в иной форме.

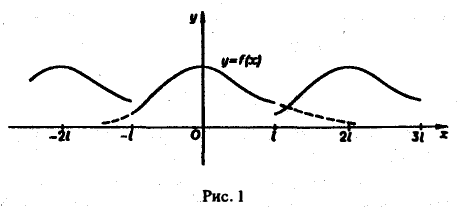
С этой целью внесем в него из формул (2) значения коэффициентов а» и оп, подведем под знаки интегралов cos ^ х и sin х (что возможно, поскольку переменной интегрирования является т) О) и используем формулу для косинуса разности. Будем иметь Если функция/(ж) первоначально была определена на интервале числовой оси, большем, чем отрезок [-1,1] (например, на всей оси), то разложение (3) воспроизведет значения этой функции только на отрезке [-1,1] и продолжит се на всю числовую ось как периодическую функцию с периодом 21 (рис. 1).

Поэтому, если функция f(x) (вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно попытаться перейти к пределу при I +оо. При этом естественно потребовать выполнения следующих условий: 1. f(x) удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох 2. функция f(x) абсолютно интегрируема на всей числовой оси, При выполнении условия 2 первое слагаемое правой части равенства (3) при I -* +оо стремится к нулю. В самом деле, Попытаемся установить, во что перейдет в пределе при I +оо сумма в правой, части (3).

Возможно вам будут полезны данные страницы:

Положим так, что Тогда сумма в правой части (3) примет вид В силу абсолютной сходимости интеграла эта сумма при больших I мало отличается от выражения которое напоминает интегральную сумму для функции переменного £ составленную для интервала (0, +оо) изменения Поэтому естественно ожидать, что при сумма (5) перейдет в интеграл Сдругой стороны, при фиксировано) из формулы (3) вытекает, что и мы получаем равенство Достаточное условие справедливости формулы (7) выражается следующей теоремой.

Теорема 1:

Если функция f(x) абсолютно интегрируема на всей числовой оси и имеет вместе со своей производной конечное число точек разрыва первого рода на любом отрезке [а, 6], то справедливо равенство При этом во всякой точке xq, являющейся точкой разрыва 1-го рода функции /(ж), значение интеграла в правой части (7) равно Формулу (7) называют интегральной формулой Фурье, а стоящий в ее правой части интеграл — интегралом Фурье.

Если воспользоваться формулой дня косинуса разности, то формулу (7) можно записать в виде Функции а(£), Ь(£) являются аналогами соответствующих коэффициентов Фурье ап и Ьп 2тг-периодической функции, но последние определены для дискретных значений п, вто время как а(0> НО определеныдля непрерывных значений £ G (-оо, +оо). Комплексная форма интеграла Фурье Предполагая /(х) абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл Этот интеграл равномерно сходится для , так как и потому представляет собой непрерывную и, очевидно, нечетную функцию от Но тогда С другой стороны, интеграл есть четная функция переменной так что Поэтому интегральную формулу Фурье можно записать так: Умножим равенство на мнимую единицу i и прибавим к равенству (10).

Получим откуда, в силу формулы Эйлера будем иметь Это — комплексная форма интеграла Фурье. Здесь внешнее интегрирование по £ понимается в смысле главного значения по Коши: §2. Преобразование Фурье. Косинус- и синус-преобразования Фурье Пусть функция f(x) является кусочно-гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси. Определение. Функция откуда, в силу формулы Эйлера , будем иметь называется преобразованием Фурье функции /(г) (спектральной функцией).

Это — интегральное преобразование функции /(г) на интервале (-оо,+оо) с ядром Используя интегральную формулу Фурье получаем Это так называемое обратное преобразование Фурье, дающее переход от F(£) к /(х). Иногда прямое преобразование Фурье задают так: Тогда обратное преобразование Фурье определится формулой Преобразование Фурье функции /(ж) определяют также следующим образом: ПРЕОБРАЗОВАНИЕ ФУРЬЕ Интеграл Фурье Комплексная форма интеграла Преобразование Фурье Косинус и синус преобразования Амплитудный и фазовый спектры Свойства Приложения.

Тогда, в свою очередь, При этом положение множителя ^ достаточно произвольно: он может входить либо в формулу (1″), либо в формулу (2″).

Пример 1. Найти преобразование Фурье функции -4 Имеем Это равенство допуска ет дифференцирование по £ под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда < принадлежит любому конечному отрезку): Интегрируя по частям, будем иметь Внеинтегральное слагаемое обращается в нуль, и мы получаем откуда (С — постоянная интегрирования).

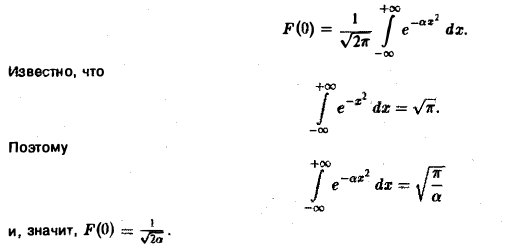
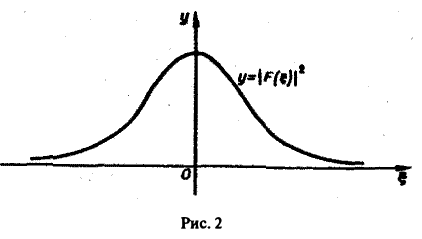
Полагая в (4) £ = 0, найдем С = F(0). В силу (3) имеем Известно, что В частности, для ) получаем, что Пример 2 (разред кокдемсетора через сопропиление). Рассмотрим функцию 4 Для спектрам ыюй функции F(£) получаем Отсюда (рис.2). Условие абсолютной интегри-руемости функции f(x) на всей числовой оси является весьма жестким. Оно исключает, например, такие элементарные функции, как ) = cos ж, f(x) = е1, для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует.

Фурье-образ имеют только те функции, которые достаточно быстро стремятся к нулю при |х| -+ +оо (как в примерах 1 и 2). 2.1. Косинус- и синус-преобразования Фурье Используя формулу косинуса, разности, перепишем интегральную формулу Фурье в следующем виде: Пусть f(x) — четная функция. Тогда так что изравснства (5) имеем В случае нечетной f(x) аналогично получаем Если f(x) задана лишь на (0, -foo), то формула (6) продолжает f(x) на всю ось Ох четным образом, а формула (7) — нечетным. (7) Определение.

Функция называется косинус-преобразованием Фурье функции f(x). Из (6) следует, что для четной функции f(x) Это означает, что f(x), в свою очередь, является косинус-преобразованием для Fc(£). Иными словами, функции / и Fc являются взаимными косинус-преобразованиями. Определение. Функция называется синус-преобразованием Фурье функции f(x). Из (7) получаем, что для нечетной функции f(x) т.е. f и Fs являются взаимными синус-преобразованиями.

Пример 3 прамоугольный импульс:

Пусть f(t) — четная функция, определенная следующим образом: (рис. 3). Воспользуемся полученным результатом для вычисления интеграла В силу формулы (9) имеем Рис.3 0 0 В точке t = 0 функция f(t) непрерывна и равна единице. Поэтому из (12′) получим 2.2. Амплитудный и фазовый спектры интеграла Фурье Пусть периодическая с периодом 2т функция /(х) разлагается в ряд Фурье Это равенство можно записать в виде где — амплитуда колебания с частотой п, — фаза. На этом пути мы приходим к понятиям амплитудного и фазового спектров периодической функции.

Пример 4:

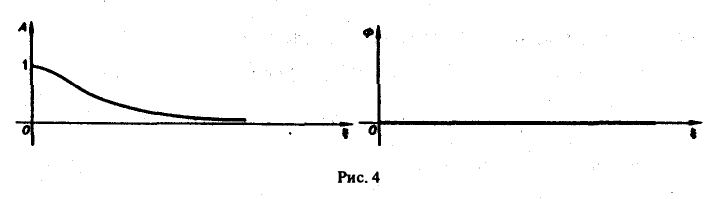
Найти амплитудный и фазовый спектры функции 4 Находим спектральную функцию Отсюда Графики этих функций изображены на рис. 4. §3. Свойства преобразования Фурье 1. Линейность. Если и G(0 — преобразования Фурье функций /(х) и д(х) соответственно, то при любых постоянных а и р преобразованием Фурье функции a f<x) + р д(х) будет функция a Пользуясь свойством линейности интеграла, имеем Таким образом, преобразование Фурье есть линейный оператор. Обозначая его через будем писать

интегрируемой на всей числовой оси функции /(ж), то F(() ограничена при всех . Пусть функция f(x) абсолютно интегрируема на всей оси — преобразование Фурье функции f(x). Тогда 3«fltsJ. Пусть f(x) — функция, допуска кнцэя преобразование Фурье, Л — дойств ительяов число. Фуниция fh(x) = f <z-h) называется сдвигом фунждии fh — действительное число. Показать, что 3. Преобразование Фурье и ооерэции дифференцирования.

Пусть абсолютно интегрируемая функция f(x) имеет производную f'(x), также абсолютно интегрируемую на всей оси Ох, так что /(я) стремится к нулю при |ж| —» +оо. Считая f'(x) гладкой функцией, запишем Интегрируя по частям, будем иметь Внеинтегральноеслагаемое обращается в нуль (так как , и мы получаем Таким образом, дифференцированию функции /(х) отвечает умножение ее образа Фурье ^П/] на множитель.

Если функция f(x) имеет глад*«е абсолютно интефируемые производные до порядка m включительно и все они, как и сама функция f(x), стремятся к нулю при то, интегрируя по частям нужное число раз, получим Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину и тем самым упрощает задачуинтегрирования некоторых видов дифференциальных уравнений.

Так как преобразование Фурье абсолютно интегрируемой функции f^kx) есть ограниченная функция от (свойство 2), то из соотношения (2) получаем для следующую оценку: ПРЕОБРАЗОВАНИЕ ФУРЬЕ Интеграл Фурье Комплексная форма интеграла Преобразование Фурье Косинус и синус преобразования Амплитудный и фазовый спектры Свойства Приложения Из этой оценки следует: чем больше функция f(x) имеет абсолютно интегрируемых производных, тем быстрее ее преобразование Фурье стремится к нулю при .

Замечание. Условие является достаточно естественным, поскольку обычная 1еория интегралов Фурье имеет дело с процессами, которые в том или ином смысле имеют начало и коней, но не продолжаются неограниченно с примерно одинаковой интенсивностью. 4. Связь между скоростью убывания функции f(x) при |z| —» -f оо и гладкостью ее преобразования Фурм. Предположим, что не только /(х), но и ее произведение xf(x) является абсолютно интегрируемой функцйей на всей оси Ох. Тогда преобразование Фурье ) будет дифференцируемой функцией.

Действительно, формальное дифференцирование по параметру £ подынтегральной функции приводит к интегралу который является абсолютно и равномерно сходящимся относительно параметра Следовательно, дифференцирование возможно, и Таким образом, т. е. операция умножения f(x) на аргумент х переходит после преобразования Фурье в операцию t щ. Если вместе с функцией f(x) абсолютно интегрируемыми на всей оси Ох являются функции , то процесс дифференцирования можно продолжить.

Получим, что функция имеет производные до порядка m включительно, причем Таким образом, чем быстрее функция f(x) убывает при тем более гладкой получается функция Теорема 2 (о сверле). Пусть- преобразования Фурье функций /,(ж) и f2(x) соответственно. Тогда причем двойной интеграл в правой части сходится абсолютно. Положим — х. Тогда будем иметь или, меняя порядок интегрирования, Функция называется сверткой функций и обозначается символом Формула (1) может быть теперь записана так: Отсюда видно, что преобразование Фурье свертки функций f(x) и f2(x) равно умноженному на у/2ж произведению преобразований Фурье свертываемых функций, Замечание.

Нетрудно установить следующие свойства свертки: 1) линейность: 2) коммутативность: §4. Приложения преобразования Фурье 1. Пусть Р(^) — линейный дифференциальный оператор порядка m с постоянными коэффициентами, Используя формулу для преобразования Фурье производных функции у(х), находим ‘ Рассмотрим дифференциальное уравнение где Р — введенный выше дифференциальный оператор. Предположим, что искомое решение у(х) имеет преобразование Фурье у (О. а функция f(x) имеет преобразование /(£)•

Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси относительно откуда так что формально где символ обозначает обратное преобразование Фурье. Основное ограничение применимости этого метода связано со следующим фактом. Решение обыкновенного дифференциального уравнения с постоянными коэффициентами содержит функции вида еЛ*, eaz cos fix, еах sin рх. Они не являются абсолютно интегрируемыми на оси -оо

Это ограничение можно обойти, если ввести в рассмотрение так называемые обобщенные функции. Однако в ряде случаев преобразование Фурье все же применимо в своей классической форме. Пример. Найти решение а = а(х, t) уравнения (а = const), при начальных условиях Это — задача о свободных колебаниях бесконечной однородной струны, когда задано начальное отклонение

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Интеграл ФурьеСкачать

Преобразование Фурье с примерами решения и образцами выполнения

Одним из мощных средств исследования задач математической физики является метод интегральных преобразований.

Пусть функция f(x) задана на интервале (а, 6), конечном или бесконечном. Интегральным преобразованием функции f(х) называется функция (*)

где К(х, w) — фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существует в собственном или несобственном смысле).

Видео:Курс по ИДУ: Применение ИПФ к решению интегральных и дифференциальных уравнений | Занятие 10Скачать

Интеграл Фурье

Всякая функция f(x), которая на отрезке [— l, l] удовлетворяет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом (1)

Коэффициенты аn и bn ряда (1) определяются по формулам Эйлера—Фурье:
(2)

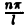
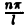
Ряд в правой части равенства (1) можно записать в иной форме. С этой целью внесем в него из формул (2) значения коэффициентов аn и bn, подведем под знаки интегралов cos х и sin х (что возможно, поскольку переменной интегрирования является τ) и используем формулу для косинуса разности. Будем иметь
(3)

Если функция f(x) первоначально была определена на интервале числовой оси, большем, чем отрезок [-l, l] (например, на всей оси), то разложение (3) воспроизведет значения этой функции только на отрезке [-l, l] и продолжит ее на всю числовую ось как периодическую функцию с периодом 2l (рис. 1).

Поэтому, если функция f(x) (вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно попытаться перейти к пределу при l → +∞. При этом естественно потребовать выполнения следующих условий:

1, f(x) удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох;

2. функция f(x) абсолютно интегрируема на всей числовой оси,

При выполнении условия 2 первое слагаемое правой части равенства (3) при l → +∞ стремится к нулю. В самом деле,

Попытаемся установить, во что перейдет в пределе при l → +∞ сумма в правой части (3). Положим

так, что 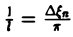. Тогда сумма в правой части (3) примет вид

В силу абсолютной сходимости интеграла эта сумма при больших l мало отличается от выражения

которое напоминает интегральную сумму для функции переменного ξ

составленную для интервала (0, + ∞) изменения Поэтому естественно ожидать, что при l → +∞ ( 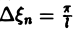→ 0) сумма (5) перейдет в интеграл

С другой стороны, при l → +∞ (х фиксировано) из формулы (3) вытекает, что

и мы получаем равенство
(7)

Достаточное условие справедливости формулы (7) выражается следующей теоремой.

Теорема:

Если функция f(x) абсолютно интегрируема на всей числовой оси — ∞

При этом во всякой точке xq, являющейся точкой разрыва 1-го рода функции f(x), значение интеграла в правой части (7) равно

Формулу (7) называют интегральной формулой Фурье, а стоящий в ее правой части интеграл — интегралам Фурье.

Если воспользоваться формулой для косинуса разности, то формулу (7) можно записать в виде (8)

Функции а( ξ ), b( ξ ) являются аналогами соответствующих коэффициентов Фурье an и bn 2π-периодической функции, но последние определены для дискретных значений п, в то время как а( ξ ), b( ξ ) определены для непрерывных значений ξ ∈ (— ∞, + ∞).

Видео:AGalilov: Преобразование Фурье "на пальцах"Скачать

Комплексная форма интеграла Фурье

Предполагая f(x) абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл

Этот интеграл равномерно сходится для — ∞

и потому представляет собой непрерывную и, очевидно, нечетную функцию от ξ. Но тогда

С другой стороны, интеграл

есть четная функция переменной так что

Поэтому интегральную формулу Фурье можно записать так:

на мнимую единицу i и прибавим к равенству (10). Получим

откуда, в силу формулы Эйлера (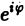= cos φ + i sin φ), будем иметь
(11)

Это — комплексная форма интеграла Фурье. Здесь внешнее интегрирование по ξ понимается в смысле главного значения по Коши:

Видео:13.2 Разложение функции в ряд Фурье. Пример 1.Скачать

Преобразование Фурье. Косинус- и синус-преобразования Фурье

Пусть функция f(x) является кусочно-гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси.

Определение:

называется преобразованием Фурье функции f(x) (спектральной функцией).

Это — интегральное преобразование функции f(x) на интервале (- ∞ ,+ ∞) с ядром

Используя интегральную формулу Фурье

Это так называемое обратное преобразование Фурье, дающее переход от F( ξ ) к f(x). Иногда прямое преобразование Фурье задают так:

Тогда обратное преобразование Фурье определится формулой

Преобразование Фурье F( ξ ) функции f(х) определяют также следующим образом:

Тогда, в свою очередь,

При этом положение множителя 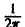достаточно произвольно: он может входить либо в формулу (1″), либо в формулу (2″).

Пример:

Найти преобразование Фурье функции

Это равенство допускает дифференцирование по ξ под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда ξ принадлежит любому конечному отрезку):

Интегрируя по частям, будем иметь

Внеинтегральное слагаемое обращается в нуль, и мы получаем

(С — постоянная интегрирования). Полагая в (4) ξ = 0, найдем С —F(0). В силу (3) имеем

В частности, для

Пример:

Разряд конденсатора через сопротивление. Рассмотрим функцию

Для спектральной функции F( ξ ) получаем

Условие абсолютной интегрируемости функции f(x) на всей числовой оси является весьма жестким. Оно исключает, например, такие элементарные функции, как f(x) = 1. f(x) = x 3 , f(х) = cosx, f(х) = е х , для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует.

Фурье-образ имеют только те функции, которые достаточно быстро стремятся к нулю при |х| → + ∞ (как в примерах 1 и 2).

Видео:Интеграл Фурье и преобразование ФурьеСкачать

Косинус- и синус-преобразования Фурье

Используя формулу косинуса, разности, перепишем интегральную формулу Фурье

в следующем виде:

Пусть f(x) — четная функция. Тогда

так что из равенства (5) имеем
(6)

В случае нечетной f(x) аналогично получаем
(7)

Если f(х) задана лишь на (0, + ∞), то формула (6) продолжает f(x) на всю ось Ох четным образом, а формула (7) — нечетным.

Определение:

называется косинус-преобразованием Фурье функции f(x). Из (6) следует, что для четной функции f(x)

Это означает, что f(x), в свою очередь, является косинус-преобразованием для Fc( ξ ). Иными словами, функции f и Fc являются взаимными косинус-преобразованиями.

Определение:

называется синус-преобразованием Фурье функции f(x).
Из (7) получаем, что для нечетной функции f(х)

т.е. f и Fs являются взаимными синус-преобразованиями.

Пример:

Прямоугольный импульс. Пусть f(t) — четнaя функция, определенная следующим образом:

Воспользуемся полученным результатом для вычисления интеграла

В силу формулы (9) имеем

В точке t = 0 функция f(t) непрерывна и равна единице.

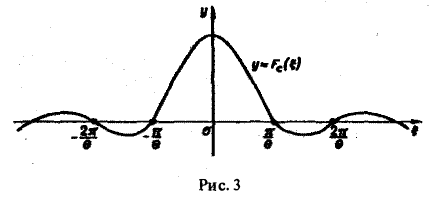
Поэтому из (12′) получим

Видео:Интегральное преобразование ФурьеСкачать

Амплитудный и фазовый спектры интеграла Фурье

Пусть периодическая с периодом 2π функция f(х) разлагается в ряд Фурье

Это равенство можно записать в виде

где Cn = 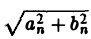— амплитуда колебания с частотой п, φn — фаза. На этом пути мы приходим к понятиям амплитудного и фазового спектров периодической функции.

Для непериодической функции f(x), заданной на (- ∞, + ∞), при определенных условиях оказывается возможным представить ее интегралом Фурье

осуществляющим разложение этой функции по всем частотам 0

(прямое преобразование Фурье функции f(х)).

называется амплитудным спектром, а функция

(0 — фазовым спектром функции f(x).

Амплитудный спектр A (ξ) служит мерой вклада частоты ξ в функцию f(х).

Пример:

Найти амплитудный и фазовый спектры функции

Находим спектральную функцию

Графики этих функций изображены на рис. 4.

Видео:Преобразование ФурьеСкачать

Свойства преобразования Фурье

1, Линейность. Если F( ξ ) и G( ξ ) — преобразования Фурье функций f(х) и g(х) соответственно, то при любых постоянных а и β преобразованием Фурье функции а f(х) + β g(х) будет функция a F( ξ ) + βG( ξ ).

Пользуясь свойством линейности интеграла, имеем

Таким образом, преобразование Фурье есть линейный оператор. Обозначая его через будем писать

Если F( ξ ) есть преобразование Фурье абсолютно интегрируемой на всей числовой оси функции f(х), то F( ξ ) ограничена при всех ξ ∈ (— ∞, + ∞).

Пусть функция f(х) абсолютно интегрируема на всей оси — ∞

— преобразование Фурье функции f(х). Тогда

Задача:

Пусть f(x) — функция, допускающая преобразование Фурье, h — действительное число. Функция fh(x) = f(x-h) называется сдвигом функции f(x). Пользуясь определением преобразования Фурье, показать, что

Задача:

Пусть функция f(x) имеет преобразование Фурье F( ξ ), h — действительное число. Показать, что

3. Преобразование Фурье и операция дифференцирования. Пусть абсолютно интегрируемая функция f(х) имеет производную f'(х), также абсолютно интегрируемую на всей оси Ох, так что f(х) стремится к нулю при |х| —► + ∞. Считая f'(х) гладкой функцией, запишем

Интегрируя по частям, будем иметь

Внеинтегральное слагаемое обращается в нуль (так как f(х) → 0 при |х| → + ∞), и мы получаем (1)

Таким образом, дифференцированию функции f(х) отвечает умножение ее образа Фурье [f] на множитель iξ.

Если функция f(х) имеет гладкие абсолютно интегрируемые производные до порядка m включительно и все они, как и сама функция f(х), стремятся к нулю при |x| → + ∞, то, интегрируя по частям нужное число раз, получим

Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину iξ и тем самым упрощает задачу интегрирования некоторых видов дифференциальных уравнений.

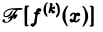
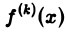
Так как преобразование Фурье абсолютно интегрируемой функции есть ограниченная функция от ξ (свойство 2), то из соотношения (2) получаем для [f] следующую оценку:

Из этой оценки следует: чем больше функция f(х) имеет абсолютно интегрируемых производных, тем быстрее ее преобразование Фурье стремится к нулю при | ξ | → + ∞.

Замечание:

Условие 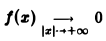является достаточно естественным, поскольку обычная теория интегралов Фурье имеет дело с процессами, которые в том или ином смысле имеют начало и конец, но не продолжаются неограниченно с примерно одинаковой интенсивностью.

4. Связь между скоростью убывания функции f(x) при |х| → + ∞ и гладкостью ее преобразования Фурье. Предположим, что не только f(x), но и ее произведение хf(х) является абсолютно интегрируемой функцией на всей оси Ох. Тогда преобразование Фурье

функции f(x) будет дифференцируемой функцией.

Действительно, формальное дифференцирование по параметру ξ подынтегральной функции приводит к интегралу

который является абсолютно и равномерно сходящимся относительно параметра Следовательно, дифференцирование возможно, и

т. е. операция умножения f(х) на аргумент х переходит после преобразования Фурье в операцию

Если вместе с функцией f(х) абсолютно интегрируемыми на всей оси Ох являются функции хf(х)…..х m f(х), то процесс дифференцирования можно продолжить.

Получим, что функция F( ξ ) = [f(х)] имеет производные до порядка m включительно, причем

Таким образом, чем быстрее функция f(х) убывает при |х| → + ∞, тем более гладкой получается функция F( ξ ) = [f(х)].

Теорема:

О свертке. Пусть F1( ξ ) и F2( ξ ) — преобразования Фурье функций f1(x) и f2(x) соответственно. Тогда

причем двойной интеграл в правой части сходится абсолютно.

Положим х + у = т, так что у = т — х. Тогда будем иметь

или, меняя порядок интегрирования,

называется сверткой функций f(x) и f2(x) и обозначается символом 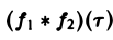. Формула (1) может быть теперь записана так:

Отсюда видно, что преобразование Фурье свертки функций f1(x) и f2(x) равно умноженному на 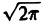произведению преобразований Фурье свертываемых функций,

Замечание:

Нетрудно установить следующие свойства свертки:

Видео:Интеграл Фурье, преобразование ФурьеСкачать

Приложения преобразования Фурье

1, Пусть 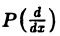— линейный дифференциальный оператор порядка m с постоянными коэффициентами,

(аo, a1,… ,ат = const). Используя формулу для преобразования Фурье производных функции у(х), находим

Рассмотрим дифференциальное уравнение

где 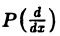— введенный выше дифференциальный оператор.

Предположим, что искомое решение у(х) имеет преобразование Фурье y(ξ), а функция f(x) имеет преобразование f( ξ ). Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси Oξ относительно y(ξ)

так что формально

где символ 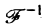обозначает обратное преобразование Фурье.

Основное ограничение применимости этого метода связано со следующим фактом. Решение обыкновенного дифференциального уравнения с постоянными коэффициентами содержит функции вида

Они не являются абсолютно интегрируемыми на оси — ∞

(а = const), при начальных условиях

Это — задача о свободных колебаниях бесконечной однородной струны, когда задано начальное отклонение φ(х) точек струны, а начальные скорости отсутствуют.

Поскольку пространственная переменная х изменяется в пределах от — ∞ до + ∞, подвергнем уравнение и начальные условия преобразованию Фурье по переменной х. Будем предполагать, что

1) функции u(z, t) и φ(x) — достаточно гладкие и стремятся к нулю при х → + ∞ и ∀t ≥ О настолько быстро, что существуют преобразования Фурье

2) допустимы операции дифференцирования, так что

Умножая обе части (2) на 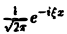и интегрируя по x от — ∞ до + ∞, получим

а из начальных условий (3) найдем

Таким образом, применяя к задаче (2)-(3) преобразование Фурье, приходим к задаче Коши (8)—(10) для обыкновенного дифференциального уравнения, где ξ — параметр. Решением уравнения (8) является функция

Из условий (9) и (10) находим, что С1( ξ ) = φ( ξ ). C2( ξ ) = 0, так что v( ξ, t) = φ( ξ )cos aξt. Применяя обратное преобразование Фурье, получим

Это частный случай формулы Даламбера решения задачи (2)-(3).

2. Преобразование Фурье может быть использовано при решении некоторых интегральных уравнений, т. е. уравнений, в которых неизвестная функция входит под знак интеграла.

Рассмотрим, например, уравнение

где φ(х) — искомая функция. Записав (1) в виде

замечаем, что левую часть (2) можно рассматривать как преобразование Фурье функции φ(х), так что (2) равносильно следующему равенству:

Тогда по формуле обращения

Функция 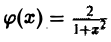есть решение уравнения (1).

Видео:Простейшие интегральные уравненияСкачать

Понятие о многомерном преобразовании Фурье

Преобразование Фурье:

Многомерным преобразованием Фурье абсолютно интегрируемой функции f(х1, х2,…, хb) называется функция

символ 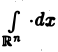обозначает интегрирование по всему пространству R n .

Свойства многомерного преобразования аналогичны соответствующим свойствам преобразования Фурье функции одной переменной. В специальном случае, когда

Видео:Курс по ИДУ: Интеграл и преобразование Фурье | Занятие 3Скачать

Дополнение к преобразованию Фурье

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Что такое ряды Фурье и с чем их едят - bezbotvyСкачать

Простыми словами о преобразовании Фурье

Я полагаю что все в общих чертах знают о существовании такого замечательного математического инструмента как преобразование Фурье. Однако в ВУЗах его почему-то преподают настолько плохо, что понимают как это преобразование работает и как им правильно следует пользоваться сравнительно немного людей. Между тем математика данного преобразования на удивление красива, проста и изящна. Я предлагаю всем желающим узнать немного больше о преобразовании Фурье и близкой ему теме того как аналоговые сигналы удается эффективно превращать для вычислительной обработки в цифровые.

(с) xkcd

Без использования сложных формул и матлаба я постараюсь ответить на следующие вопросы:

• FT, DTF, DTFT — в чем отличия и как совершенно разные казалось бы формулы дают столь концептуально похожие результаты?
• Как правильно интерпретировать результаты быстрого преобразования Фурье (FFT)
• Что делать если дан сигнал из 179 сэмплов а БПФ требует на вход последовательность по длине равную степени двойки
• Почему при попытке получить с помощью Фурье спектр синусоиды вместо ожидаемой одиночной “палки” на графике вылезает странная загогулина и что с этим можно сделать
• Зачем перед АЦП и после ЦАП ставят аналоговые фильтры
• Можно ли оцифровать АЦП сигнал с частотой выше половины частоты дискретизации (школьный ответ неверен, правильный ответ — можно)
• Как по цифровой последовательности восстанавливают исходный сигнал

Я буду исходить из предположения что читатель понимает что такое интеграл, комплексное число (а так же его модуль и аргумент), свертка функций, плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака. Не знаете — не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”

Начать надо, наверное, с того что обычное преобразование Фурье — это некая такая штука которая, как можно догадаться из названия, преобразует одни функции в другие, то есть ставит в соответствие каждой функции действительного переменного x(t) её спектр или фурье-образ y(w):

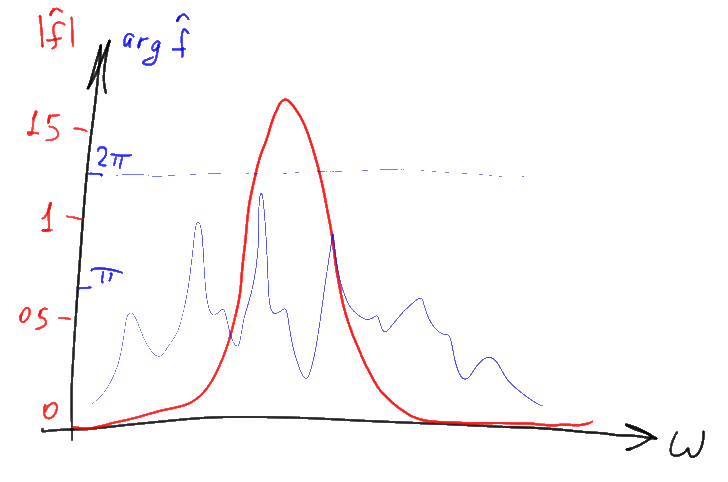
Если приводить аналогии, то примером аналогичного по смыслу преобразования может послужить например дифференцирование, превращающее функцию в её производную. То есть преобразование Фурье — такая же, по сути, операция как и взятие производной, и её часто обозначают схожим образом, рисуя треугольную “шапочку” над функцией. Только в отличие от дифференцирования которое можно определить и для действительных чисел, преобразование Фурье всегда “работает” с более общими комплексными числами. Из-за этого постоянно возникают проблемы с отображением результатов этого преобразования, поскольку комплексные числа определяются не одной, а двумя координатами на оперирующем действительными числами графике. Удобнее всего, как правило, оказывается представить комплексные числа в виде модуля и аргумента и нарисовать их по раздельности как два отдельных графика:

График аргумента комплексного значения часто называют в данном случае “фазовым спектром”, а график модуля — “амплитудным спектром”. Амплитудный спектр как правило представляет намного больший интерес, а потому “фазовую” часть спектра нередко пропускают. В этой статье мы тоже сосредоточимся на “амплитудных” вещах, но забывать про существование пропущенной фазовой части графика не следует. Кроме того, вместо обычного модуля комплексного значения часто рисуют его десятичный логарифм умноженный на 10. В результате получается логарифмический график, значения на котором отображаются в децибелах (дБ).

Обратите внимание что не очень сильно отрицательным числам логарифмического графика (-20 дБ и менее) при этом соответствуют практически нулевые числа на графике “обычном”. Поэтому длинные и широкие “хвосты” разнообразных спектров на таких графиках при отображении в “обычные” координаты как правило практически исчезают. Удобство подобного странного на первый взгляд представления возникает из того что фурье-образы различных функций часто необходимо перемножать между собой. При подобном поточечном умножении комплекснозначных фурье-образов их фазовые спектры складываются, а амплитудные — перемножаются. Первое выполняется легко, а второе — сравнительно сложно. Однако логарифмы амплитуды при перемножении амплитуд складываются, поэтому логарифмические графики амплитуды можно, как и графики фаз, просто поточечно складывать. Кроме того, в практических задачах часто удобнее оперировать не «амплитудой» сигнала, а его «мощностью» (квадратом амплитуды). На логарифмической шкале оба графика (и амплитуды и мощности) выглядят идентично и отличаются только коэффициентом — все значения на графике мощности ровно вдвое больше чем на шкале амплитуд. Соответственно для построения графика распределения мощности по частоте (в децибелах) можно не возводить ничего в квадрат, а посчитать десятичный логарифм и умножить его на 20.

Заскучали? Погодите, еще немного, с занудной частью статьи, объясняющей как интерпретировать графики, мы скоро покончим :). Но перед этим следует понять одну крайне важную вещь: хотя все вышеприведенные графики спектров были нарисованы для некоторых ограниченных диапазонов значений (в частности, положительных чисел), все эти графики на самом деле продолжаются в плюс и минус бесконечность. На графиках просто изображается некоторая “наиболее содержательная” часть графика, которая обычно зеркально отражается для отрицательных значений параметра и зачастую периодически повторяется с некоторым шагом, если рассматривать её в более крупном масштабе.

Определившись с тем, что же рисуется на графиках, давайте вернемся собственно к преобразованию Фурье и его свойствам. Существует несколько разных способов как определить это преобразование, отличающихся небольшими деталями (разными нормировками). Например в наших ВУЗах почему-то часто используют нормировку преобразования Фурье определяющую спектр в терминах угловой частоты (радианов в секунду). Я буду использовать более удобную западную формулировку, определяющую спектр в терминах обычной частоты (герцах). Прямое и обратное преобразование Фурье в этом случае определяются формулами слева, а некоторые свойства этого преобразования которые нам понадобятся — списком из семи пунктов справа:

Первое из этих свойств — линейность. Если мы берем какую-то линейную комбинацию функций, то преобразование Фурье этой комбинации будет такой же линейной комбинацией образов Фурье этих функций. Это свойство позволяет сводить сложные функции и их фурье-образы к более простым. Например, фурье-образ синусоидальной функции с частотой f и амплитудой a является комбинацией из двух дельта-функций расположенных в точках f и -f и с коэффициентом a/2:

Если взять функцию, состоящую из суммы множества синусоид с разными частотами, то согласно свойству линейности, фурье-образ этой функции будет состоять из соответствующего набора дельта-функций. Это позволяет дать наивную, но наглядную интерпретацию спектра по принципу “если в спектре функции частоте f соответствует амплитуда a, то исходную функцию можно представить как сумму синусоид, одной из которых будет синусоида с частотой f и амплитудой 2a”. Строго говоря, эта интерпретация неверна, поскольку дельта-функция и точка на графике — это совершенно разные вещи, но как мы увидим дальше, для дискретных преобразований Фурье она будет не так уж и далека от истины.

Второе свойство преобразования Фурье — это независимость амплитудного спектра от сдвига сигнала по времени. Если мы подвинем функцию влево или вправо по оси x, то поменяется лишь её фазовый спектр.

Третье свойство — растяжение (сжатие) исходной функции по оси времени (x) пропорционально сжимает (растягивает) её фурье-образ по шкале частот (w). В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности.

Четвертое и пятое свойства самые, пожалуй, полезные из всех. Они позволяют свести свертку функций к поточечному перемножению их фурье-образов и наоборот — поточечное перемножение функций к свертке их фурье-образов. Чуть дальше я покажу насколько это удобно.

Шестое свойство говорит о симметрии фурье-образов. В частности, из этого свойства следует что в фурье-образе действительнозначной функции (т.е. любого “реального” сигнала) амплитудный спектр всегда является четной функцией, а фазовый спектр (если его привести к диапазону -pi. pi) — нечетной. Именно по этой причине на графиках спектров практически никогда не рисуют отрицательную часть спектра — для действительнозначных сигналов она не дает никакой новой информации (но, повторюсь, и нулевой при этом не является).

Наконец последнее, седьмое свойство, говорит о том, что преобразование Фурье сохраняет “энергию” сигнала. Оно осмысленно только для сигналов конечной продолжительности, энергия которых конечна, и говорит о том, что спектр подобных сигналов на бесконечности быстро приближается к нулю. Именно в силу этого свойства на графиках спектров как правило изображают только “основную” часть сигнала, несущую в себе львиную долю энергии — остальная часть графика просто стремится к нулю (но, опять же, нулем не является).

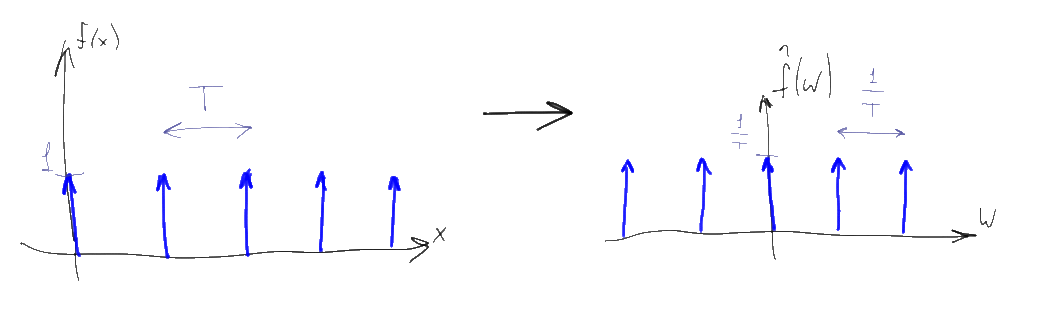
Вооружившись этими 7 свойствами, давайте посмотрим на математику “оцифровки” сигнала, позволяющую перевести непрерывный сигнал в последовательность цифр. Для этого нам понадобится взять функцию, известную как “гребенка Дирака”:

Гребенка Дирака — это просто периодическая последовательность дельта-функций с единичным коэффициентом, начинающаяся в нуле и идущая с шагом T. Для оцифровки сигналов, T выбирают по возможности малым числом, T

📹 Видео

Курс по ИДУ: Численное решение интегральных уравнений | Занятие 14Скачать

13.1. Что такое ряд Фурье?Скачать

Преобразование Фурье | Введение | Часть 1Скачать

Метод интегральных преобразований - 3Скачать

ЗАЧЕМ в жизни нужно преобразование Фурье? В Первом Приближении. Чуть-Чуть о Науке #НаукаСкачать