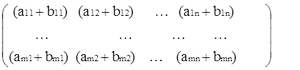Решение экономических задач с применением матриц и систем линейных уравнений теория (7 видео)

Методы решения систем уравнений и их применение при решении экономических задач

Уметь решать систему уравнений нужно не только и не столько в задачах, начинающихся словами «решить систему …», хотя такие задачи встречаются наиболее часто. Кроме этого, решение многих текстовых задач немыслимо без навыков работы с системами уравнений. Причем зачастую проблема состоит не в том, чтобы записать систему, адекватную текстовому условию задачи, а в том, чтобы эту систему решить!

Решить систему уравнений — это значит найти все её решения или установить, что их нет.

Существует множество методов решения системы уравнений: метод подстановки, метод алгебраического сложения, метод замены переменных, графический метод и др. Подход зависит от типа системы. Так, решение систем линейных уравнений полностью исследовано: у них найдены аналитические методы (метод Крамера) и предложено несколько численных как точных (простейший — метод Гаусса), так и приближённых (метод итераций).

Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.

При моделировании экономических задач, таких как задачи управления и планирования производства, определения оптимального размещения оборудования, оптимального плана производства, оптимального плана перевозок грузов (транспортная задача), распределения кадров и др., может быть положена гипотеза линейного представления реального мира.

Математические модели таких задач представляются линейными уравнениями. Если задача многомерна, то ее математическая модель представляется системой линейных уравнений.

Данная работа актуальна с точки зрения освоения материала и для практического применения знаний не только в математике, но и в реальных жизненных ситуациях. Например, особенно часто применять такие знания требуется в экономической сфере.

Цель работы – исследовать теоретические и практические основы эффективности использования различных методов решения систем уравнений и их применения при решении экономических задач.

Для достижения указанной цели решаются следующие задачи:

· изучить теоретические основы систем уравнений;

· рассмотреть основные методы решения систем уравнений;

· исследовать эффективность методов на конкретных примерах при решении экономических задач.

Предметом исследования являются методы решения систем уравнения.

Содержание

Творческие проекты и работы учащихся
Подробнее о проекте:
Оглавление
Введение
Немного истории
Матрицы и операции над ними
Решение с помощью матриц экономических задач
Заключение
Используемая литература
Приложение. Операции над матрицами
Реферат по математике 11 класс «Матричная алгебра в экономике»
Матричные методы при решении экономических задач
🎥 Видео

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Творческие проекты и работы учащихся

В процессе работы над индивидуальным проектом по математике «Матричная алгебра в экономике» учеником 11 класса гимназии были рассмотрены матричные методы в экономике на примерах решения задач экономического содержания. В работе доступно объясняется, что такое «математическая матрица» и как ее применять.

Подробнее о проекте:

Готовый творческий и исследовательский проект по математике «Матричная алгебра в экономике» наглядно демонстрирует взаимосвязь математики и экономики, определяет роль математических методов в анализе экономических процессов, объектов и явлений.

Введение

На современном этапе экономические взаимоотношения между субъектами образуют экономические системы со сложной структурой, большим количеством элементов и связей между ними, которые являются причиной почти всех особенностей экономических задач.

На внедрение и развитие математических методов в решении экономических задач, большое влияние оказало создание и развитие современной вычислительной техники. Вычислительная техника нового поколения позволила применять на практике множество новых методов, которые были описаны ранее только в теории или объяснялись на простых примерах.

Но никакая вычислительная техника не способна заменить человека и поэтому, люди должны уметь эффективно использовать теоретические знания в области математики в экономике, а именно, уметь правильно решать экономические задачи при помощи матричных методов.

Понятие матрицы и основанный на нем раздел математики — матричная алгебра — имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное — компактной матричной форме.

Также матрицы позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал, различные исходные данные, характеризующие уровень, структуру, особенности социально-экономического комплекса.

В современных условиях особенно актуально использование матриц для формирования баз данных, ведь вся информация обрабатывается и хранится в форме матриц.

Матрицы можно эффективно использовать не только в науке, но и применять их на практике в крупных предприятиях для решения современных экономических задач. Матричный метод позволяет упростить работу человека, уменьшить количество критериев и альтернатив для выбора и получать выгодные варианты решения для выхода из различных экономических ситуаций.

В данной работе содержится информация о самих матрицах, операциях над ними и на примерах показано, как можно решать экономические задачи при помощи матриц.

Актуальность. Математика и экономика – две на первый взгляд далекие друг от друга науки. Однако, взаимосвязь между этими науками, роль математических методов в анализе экономических процессов, объектов и явлений были отмечены учеными ещё в XVII веке.

В XX веке происходило бурное проникновение математических методов в самые разные науки, в том числе и в экономику. В настоящее время этот процесс ещё более активизировался, благодаря развитию вычислительной техники. Поэтому современному экономисту необходима основательная математическая подготовка. И в число наиболее важных математических дисциплин для экономиста входит линейная алгебра, а именно матричная алгебра. В этом я вижу актуальность выбранной темы.

Цель. Рассмотреть матричные методы в экономике на примерах решения задач экономического содержания.

На примере задач показать связь математики и экономики
Научиться применять в экономике математический аппарат
Показать роль математических методов в экономике (реальные задачи из разных сфер жизнедеятельности человека)

Гипотеза Используются ли в экономике те математические знания, которыми мы владеем

Предмет исследования: Матричные методы.

Объект исследования: Математические понятия и законы, экономические модели.

Методы исследования: Теоретическое изучение материала, образцы решения экономических задач.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Немного истории

В это же время был предложен другой метод решения систем линейных уравнений, который тоже носит имя своего изобретателя, это «метод Гаусса». Заметим, что «правило Крамера» работает только для систем с ненулевым детерминантом (определителем системы), тогда как «метод Гаусса» работает для любой системы линейных уравнений.

Огромный вклад в развитие теории матриц в середине XIX внесли такие известные ученые как Уильям Гамильтон и Артур Кэли. Наряду с ними развивали данную теорию немецкие математики Карл Вейерштрасс и Фердинанд Георг Фробениус, а также, французский математик Мари Энмон Камиль Жордан. В 1850 году Джеймс Сильвестр ввел современное понятие матрицы. Под влиянием работ этих великих ученых в математике появился новый раздел, который был назван матричной алгеброй.

Видео:Решение системы уравнений методом ГауссаСкачать

Матрицы и операции над ними

Матрица – это прямоугольная таблица, представляющая собой совокупность строк и столбцов. Размерностью матрицы называется величина m×n, где m-число строк, n-число столбцов.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате, решение систем линейных уравнений сводится к операциям над матрицами. А множество экономических задач можно свести к системам линейных уравнений.

Операции с матрицами не слишком громоздки и не требуют чрезмерно кропотливой работы; напротив, матричную алгебру во многих случаях ценят именно за краткость, простоту и ясность. С помощью матричной алгебры можно выразить в математической форме многие задачи, как большие, так и малые, независимо от их размерности.

Основные операции с матрицами рассмотрены в Приложении.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Решение с помощью матриц экономических задач

Для наглядности перейдём к рассмотрению задач.

1. С помощью матриц удобно записывать некоторые экономические зависимости. Одним из примеров может послужить таблица распределения ресурсов по различным отраслям экономики.

Таблица: Распределение ресурсов

Ресурсы	Промышленность	Сельское хозяйство	Торговля
Трудовые ресурсы	4,8	6,7	7,1
Водные ресурсы	3,1	2,5	5,8
Электроэнергия	5,6	4,3	3,4

Так, например, элемент матрицы а22 = 2,5 показывает, сколько водных ресурсов потребляет сельское хозяйство, а элемент матрицы а13 = 7,1 показывает, сколько трудовых ресурсов потребляет торговля.

2. Рассмотрим такую ситуацию. Некоторая фирма занимается реализацией четырех видов товаров в трех районах. Данные об уровне продаж товаров по районам образуют матрицу.

Величина aij, которая находится в i-й строке и j-м столбце матрицы A, обозначает количество j-го товара, проданное в i-м районе. Таким образом, строки матрицы соответствуют районам, а столбцы – видам товаров. Обозначим через ci, i= 1, 2, 3, 4 цены на реализуемые товары. Они образуют матрицу-столбец.

Если хотим найти суммарный объем продаж в первом районе, то мы должны вычислить следующее выражение:

a11c1 + a12c2 + a13c3 + a14c4,

которое является скалярным произведением первой строки матрицы A на столбец цен C. И строчка, и столбец являются арифметическими 4-х мерными векторами. Про выражение (a11c1 + a12c2 + a13c3 + a14c4) говорят, что оно получено при умножении первой строки матрицы A на столбец C.

Производя такое умножение на столбец C второй и третьей строк, получаем еще две величины, которые представляют собой суммарные продажи во втором и третьем районах. Эти две величины вместе с ранее найденной величиной образуют вектор суммарных продаж.

В этом примере фактически применено действие умножения матриц.

годовую производительность каждого предприятия по каждому виду изделий;
годовую потребность каждого предприятия по каждому виду сырья;
годовую сумму кредитования каждого предприятия для закупки сырья, необходимого для выпуска продукции указанных видов и количеств.

Решение. Нужно составить матрицы, характеризующие весь интересующий нас экономический спектр производства, а затем при помощи соответствующих операций над ними получить решение данной задачи.

Каждый столбец этой матрицы соответствует дневной производительности отдельного предприятия по каждому виду продукции. Следовательно, годовая производительность j-го предприятия по каждому виду продукции получается умножением j-гo столбца матрицы А на количество рабочих дней в году для этого предприятия (j = 1, 2, 3, 4, 5). Таким образом, годовая производительность каждого предприятия по каждому из изделий описывается матрицей.

Матрица затрат сырья на единицу изделия (эти показатели по условию одинаковы для всех предприятий) имеет вид

Дневной расход по типам сырья на предприятиях описывается произведением матрицы В на матрицу А:

где i-я строка соответствует номеру типа сырья, а j-й столбец — номеру предприятия согласно табл. 16.2 (i = 1, 2, 3; j = 1, 2, 3, 4, 5). Ответ на второй вопрос задачи получим по аналогии с матрицей Агод умножением столбцов матрицы ВА на соответствующие количества рабочих дней в году для предприятий — это годовая потребность каждого предприятия в каждом виде сырья:

Введем вектор стоимости сырья.

Тогда стоимость общего годового запаса сырья для каждого предприятия получается умножением вектора на матрицу ВAгод:

Следовательно, суммы кредитования предприятий для закупки сырья определяются соответствующими компонентами вектора .

4. Множество экономических задач можно свести к системам линейных уравнений. Для наглядного примера рассмотрим следующую задачу.

Предположим, что кривая спроса на автомобили для некоторого периода времени может быть описана уравнением

x1 = 12000 — 0,2×2,

где x1 – цена автомобиля (в долларах), а x2 – их количество.

Предполагаем также, что уравнение кривой предложения имеет вид:

Объединим уравнения в систему.

Эту систему, конечно, легко решить непосредственно, например методом подстановки. Но мы перейдем от системы к матричному уравнению.

Напрашивается решение этого уравнения в виде:

Но операции деления матриц нет. Но есть операция вычисления обратной матрицы. Подумаем, как мы решаем уравнение 5X = 7? Мы пишем, не особенно задумываясь, X = 7/5. а как записать ответ, не пользуясь делением? Это возможно: X = 5-1•7 или 7•5-1.

Обратная матрица A-1 должна обладать свойством A-1A = E, где E – единичная матрица.

Умножим слева на A-1 обе части матричного уравнения AX = В и получим равенство

Но так как A-1A =E, а EX = X, то мы приходим к равенству

Это означает, что равновесная цена на автомобили X = 4200 долларов, а объем продаж X = 39000 штук.

Подобные задачи удобно решать методом Гаусса – методом последовательного исключения переменных, который заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Преобразования Гаусса можно проводить не только с уравнениями системы, но и с матрицей их коэффициентов.

Заключение

Проанализировав применение матричной алгебры в экономике, можно прийти к выводу, что использование матриц имеет свои достоинства и недостатки.

Недостатки заключаются в том, что матричная алгебра не обеспечивает реальных рекомендаций по разработке специфических стратегий; по матрицам невозможно определить сферы бизнеса, которые готовы стать победителями.

Достоинства же применения матриц в том, что они используют широкий набор стратегически значимых переменных; указывают направление движения ресурсов; позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал, различные исходные данные, характеризующие уровень, структуру, особенности социально-экономического комплекса.

При наличии отрицательных моментов применения матричной алгебры положительная часть значительно обширнее.

Из выше рассмотренного можно сделать вывод, что роль матриц в экономике очень и очень велика. Ведь благодаря их использованию можно гораздо быстрее, чем с использованием какого-либо другого математического аппарата, и проще решить многие экономические задачи, что чрезвычайно важно для экономистов.

Используемая литература

Коршунова Н.И., Плясунов В.С. Математика в экономике. — М.:«Вита-Пресс», 1996.
Сирл С., Госман У. Матричная алгебра в экономике. – М.:Статистика, 1974.
Немцова А.В., Попова С.В. ПРИМЕНЕНИЕ СРЕДСТВ МАТРИЧНОЙ АЛГЕБРЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ ЭКОНОМИЧЕСКОГО СОДЕРЖАНИЯ // Современные наукоемкие технологии. – 2014. – № 5-2.
Ахмедханова А.И., Кожемякина В.А., Мамаев И.И. ПРИМЕНЕНИЕ МАТРИЦ В ЭКОНОМИКЕ // Международный студенческий научный вестник. – 2015. – № 3-4.;
Авдеев Д.Д., Турченко В.В. ПРИМЕНЕНИЕ МАТРИЦ В ЭКОНОМИКЕ // Научное обозрение. Педагогические науки. – 2019. – № 4-3.

Приложение. Операции над матрицами

Линейные операции над матрицами.

Определение 1. Матрицей называется прямоугольная таблица:

A = 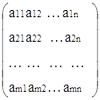= (aij)

Число m ее строк и число n ее столбцов называют размерами матрицы А. Про матрицу А говорят, что она размером m×n. Обозначим Mm×n множество матриц размером m×n (m строк и n столбцов).

Определение 2. Пусть A=(aij) и B=(bij) – две матрицы размером m×n.

Суммой матриц A и B называется матрица C=(cij) є Mm×n , такая, что cij = aij+bij для всех i и j.

Действие сложения определено для матриц одинакового размера

C=A +B=

Произведением матрицы A на число α называется матрица αA с элементами (αaij).

αA=

Операции сложения матриц и умножения матрицы на число называют линейными операциями.

+ =

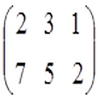
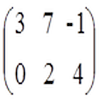
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Реферат по математике 11 класс «Матричная алгебра в экономике»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

311 лекций для учителей,
воспитателей и психологов

Получите свидетельство
о просмотре прямо сейчас!

Управление образования администрации Тогучинского района Новосибирской области

XII муниципальная научно-практическая конференция школьников

Данильченко Яна Александровна

«Матричная алгебра в экономике»

МБОУ Тогучинского района «Горновская средняя школа», 11 класс

Руководитель: Милашова Надежда Юрьевна

Квалификационная категория: Высшая

Стаж работы: 33 года

Должность: Учитель математики

Матрицы и операции над ними………. …………………….……………8

Решение экономических задач…………………………………………. 9

«Матричная алгебра в экономике»

Решение задач — важный раздел в математике. Успешное изучение математики невозможно без умения решать разнообразные задачи, поэтому я решила взять в качестве темы научно-исследовательской работы один из способов решения задач — матрицы. Этим методом можно решать и экономические задачи.

В данном исследовании, во-первых, я узнала совершенно новый для себя способ решения экономических задач — матричный метод, который мало изучается в школе. Во-вторых, научилась применять его непосредственно при решении экономических задач. Для этого я изучила и проанализировала материал по данной теме. В-третьих, показала взаимосвязь математики и экономики на примере решения задач.

Матричные модели в экономике, один из наиболее распространённых типов экономико-математических моделей.

Благодаря простоте формы и богатому экономическому содержания матричные методы находят широкое применение в различных звеньях экономики для плановых и статистических расчётов, организации нормативного хозяйства, унификации документации и сокращения документооборота, организации внутрипроизводственного хозрасчёта и для экономического анализа. Этот метод решения экономических задач помогают людям быстро и правильно решать задачи не только в жизни, но и в бизнесе.

Рецензия на проектную работу по математике на тему: «Матричная алгебра в экономике» учащейся 11А класса МБОУ Тогучинского района Горновской СОШ Данильченко Яны Александровны

Содержание работы соответствует заявленной теме и излагается согласно с удачно составленным планом, соответствует требованиям, предъявляемым к написанию исследовательской работы.

В работе определена тема, цели работы, основополагающий вопрос, а также перечислены методы исследования. Основополагающий вопрос: «Как использовать матрицы для решения экономических задач» достаточно грамотно и убедительно подтверждается материалами работы.

Яна успешно использовала теоретические и эмпирические методы. Материалы работы дают понять, что Яна предварительно внимательно изучила теорию по данной теме, показала ее практическое применение, а затем сделала собственные выводы.

Учитывая сложность предмета исследования, творческий подход и глубину анализа полученного материала, считаю работа написана хорошим литературным языком, заслуживает высокой оценки, имеет практическую значимость, и может быть удачно использована на уроках математики.

Рецензент: учитель математики Милашова Надежда Юрьевна

Математика и экономика – две на первый взгляд далекие друг от друга науки. Взаимосвязь между этими науками, роль математических методов в анализе экономических процессов, объектов и явлений были отмечены учеными ещё в XVII веке.

В XX веке происходило бурное проникновение математических методов в самые разные науки, в том числе и в экономику.

Рассмотреть матричные методы в экономике на примерах решения задач адаптированных к социально-экономическим реалиям жизни.

На примере задач показать связь математики и экономики

Научиться применять в экономике математический аппарат.

Показать роль математических методов в экономике (реальные задачи из разных сфер жизнедеятельности человека)

Используются ли в экономике те математические знания, которыми мы владеем

Математические понятия и законы, экономические модели.

Теоретическое изучение материала, образцы решения экономических задач.

Многие не знают, что такое матрица, но еще больше людей не знают, как применять матричный метод при решении экономических задач.

Меня заинтересовала эта тема, поэтому я решила посвятить свою работу этому вопросу.

Есть разные точки зрения на процессы, которые происходят в нашем обществе в настоящее время. Но независимо от того, как различные политические силы воспринимают эти процессы (как откат назад или как прогресс, движение вперед), ни одна их них не может отрицать того, что экономические условия жизни стали намного сложнее. Эти трудности не могли не вызвать волны нового интереса к математическим методам, применяемым в экономике. Следовательно, необходимо оценить роль математических методов в экономических исследованиях — насколько полно они описывают все возможные решения и предсказывают наилучшее, или даже так: стоит ли их использовать вообще?

Математические методы не стоят на месте, они постоянно развиваются, также как и сами экономические системы. Это происходит как вследствие изменений в экономике, так и по внутренней логике развития. При этом необязательно, что новые методы с неизбежностью отбрасывают старые, может происходить взаимопроникновение, включение старых теорий в новые (в качестве частного случая).

На развитие и применение математических методов огромное влияние оказало и еще окажет развитие вычислительной техники. Вычислительная техника последних поколений уже позволила на практике применить множество методов, описанных ранее лишь теоретически или на простейших примерах.

Начиная с 17 века возможности математики начинают расти.

Математика стала широко проникать во все сферы науки, и тут выяснилось, уравнения и выражения, созданные для целей одной науки, зачастую применимы, после определённой подработки, в другой.
Саму математику он рассматривает как науку о хитроумных операциях, производимых по специально разработанным правилам над специально придуманными понятиями.

Числа не имеют вкуса, запаха, веса и других характеристик, являясь лишь суждением о количестве какого-либо предмета, явления. В то же время они позволяют определить количественные характеристики и отношения практически любого объекта. исследования на опыте, на практике. Но главным критерием применимости того или иного метода является проверка результатов.

Особенности экономических задач, решаемых математическими методами
Экономическая наука, как и любая другая имеет свою специфику. Специфика ее определяется общей спецификой наук о человеке.

До того, как люди стали обмениваться продуктами своего труда, отношения между ними никак нельзя было назвать экономическими. Возникновение экономических отношений положило начало специализации труда и соответственно, всему социально-экономическому прогрессу.

На современном этапе экономические взаимоотношения между субъектами образуют экономические системы со сложной структурой, большим количеством элементов и связей между ними, которые и являются причиной почти всех особенностей экономических задач.

Прямоугольные: m и n — произвольные положительные целые числа

Матрица строка: m=1 . Во многих практических задачах такая матрица называется вектором.

Матрица столбец: n=1 . В практических задачах еще называется вектор-столбец.

Диагональная матрица: m=n и aij=0 , если i≠j .

Единичная матрица: m=n и aij =0, если i не равно j , aij =1, если i = j .

Нулевая матрица: aij=0, i=1,2. m, j=1,2. n.

Треугольная матрица: все элементы ниже главной диагонали равны 0.

Симметрическая матрица: m=n и aij=aji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы).

Что такое матрицы и операции над ними?

Матрицей называется прямоугольная таблица:

A = = ( aij )

Число m ее строк и число n ее столбцов называют размерами матрицы А. Про матрицу А говорят, что она размеров m × n .

Над матрицами можно производить действия: сложение матриц, умножение матрицы на число и умножение матриц. Эти действия по свойствам напоминают действия над числами, но есть и существенные отличия.

Например, AB ≠ BA . Действие сложения определено для матриц одинакового размера, а умножение определено, если число столбцов первого сомножителя равно числу строк второго.

Для невырожденной квадратной матрицы можно найти обратную матрицу, используя алгоритм, основанный на элементарных преобразованиях.

Систему линейных уравнений можно записать в виде матричного уравнения AX =В.

Если матрица A в этом уравнении невырожденная , то ответ можно найти по формуле:

Решение экономических задач матричным методом

Поступление товаров на первый склад описывается матрицей

а поступление товаров на второй склад описывается матрицей

Найдите суммарный завоз товаров на склады; годовой завоз на склады, если по договору, производится ежемесячный завоз одинаковых партий товаров.

Найдем суммарный завоз:

Найдем годовой завоз:

По заказу с завода в магазин доставили товары, поступление которых описывается матрицей

но данные товары не пользуются большим спросом. Найдите количество товаров, оставшихся на складе, если количество купленных товаров описывается матрицей

Найдем разность этих двух матриц:

Найти ранг матрицы А

Будем преобразовывать матрицу , проводя элементарные преобразования со строчками , которые не меняют ранга матрицы .

Прибавим ко второй строке первую . Прибавим к третьей строке первую , умноженную на 3. Получаем :

Вычитаем из третьей строки вторую:

Очевидно, что ранг матрицы меньше 3,т.к. всего 2 ненулевые строки. Более точно, ранг равен 2, т.к. , например, минор 1 -2

11 0 = 22( больше 0)

Ответ: ранг равен 2

Даны матрицы А и В. Требуется найти матрицу ( NA + TB ), где

NA = 3 * -1 2 2 = -3 6 6

TB = 2* -3 -3 2 = 6 4 -4

NA + TB = -3 6 6 + 6 4 -4 = -3+6 6+4 6-4 =

-6 -6 9 -2 -10 -6 -6-2 -6-10 9-6

Найти матрицу А^( T ), если А= 1 0

Транспортированные матрицы- это операция над матрицей. Когда ее строки становятся столбцами с теми же номеромами.

А^( T )= 1 0 Т = 1 -2

Благодаря простоте и экономическому содержанию матричные модели находят большое применение в разных разделах экономики для плановых и статистических расчётов, организации нормативного хозяйства, унификации документации и сокращения документооборота, организации внутрипроизводственного хозрасчёта и для экономического анализа.

Работа над этим проектом была интересной и увлекательной. Я выяснила, что обычные простые экономические задачи можно решать новыми, интересными и нестандартными методами. Эти методы решений помогут людям быстро и правильно решать свои задачи в бизнесе.

Коршунова Н.И., Плясунов В.С. Математика в экономике. — М.:«Вита-Пресс», 1996.

Сирл С., Госман У. Матричная алгебра в экономике. – М.:Статистика, 1974.

Петрова В.Т. Лекции по алгебре и геометрии. В 2ч.- М.:ВЛАДОС, 1999. – ч.1.

Видео:Решение системы уравнений методом Крамера.Скачать

Матричные методы при решении экономических задач

Паспорт проекта

Цель:Провести анализ использования матриц при решении экономических задач

Задачи:

1. Выявить матричные методы при решении экономических задач

2. Узнать о методе Гаусса

3. Изучить что такое матрица, и всё что связано с матрицей в экономике

4. Решить задачу по экономике

Дисциплина:Математика: Алгебра, начала математического анализа, Геометрия.

Тип проекта: исследовательская работа

Сроки реализации: 16.01.17-13.03.17

Продукт проектной деятельности:реферат.

Актуальность исследования: анализ материала, посвященного использованию матриц при решении экономических задач в учебных пособиях «Алгебра и начала анализа» разных авторов, учет целей изучения использования матриц при решении экономических задач, а так же обязательных результатов обучения, связанных с рассматриваемой темой.

СОДЕРЖАНИЕ

ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ……………..………………………

ГЛАВА 3. ПРИМЕРЫ РЕШЕНИЯ..………………………………………

Введение

Одним из основных методов решения экономических задач является матричный метод. На данный момент особенно актуально использование матриц для создания баз данных, ведь вся информация обрабатывается и хранится в матричной форме.

Впервые матрица появилась в Древнем Китае и носила название «волшебный квадрат». Чуть позже она стала известна и арабским математикам. В конце XVII века швейцарский ученый Габриэль Крамер разработал свою теорию, а в 1751 году опубликовал один из методов решения систем линейных уравнений «правило Крамера». Также в этот период был создан «метод Гаусса». Огромный вклад в развитие теории матриц в середине XIX внесли такие известные ученые как Уильям Гамильтон и Артур Кэли. Наряду с ними развивали данную теорию немецкие математики Карл Вейерштрасс и Фердинанд Георг Фробениус, а также, французский математик Мари Энмон Камиль Жордан. В 1850 году Джеймс Сильвестр ввел современное понятие матрицы. Существует целая наука, которая называется «История экономики». Она изучает, как со временем менялись хозяйственные отношения между людьми и как эта наука стала такой, какой мы видим её сейчас. Если задуматься, то становится очевидным, что экономическая наука издревле окружает нас. Например, даже в первобытном обществе существовал так называемый «натуральный обмен» — то есть люди меняли свои вещи на другие без использования денег. Постепенно появляется денежный эквивалент, роль которого исполняет золото. До сих пор запасы многих стран оцениваются в золотом эквиваленте. Сначала золоту и другим драгоценным металлам придавали форму слитков, но затем в Древней Греции и Древнем Риме начали чеканиться монеты. Монеты долгое время подразделялись на золотые, серебряные и бронзовые. В конце концов мы пришли к той валюте, что видим сейчас.

ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ

Матричные методы при решении экономических задач

Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.

На сегодняшний день известно большое количество разных мнений на процессы, которые происходят в обществе. И не важно, как разные политические силы смогут воспринять такие процессы, однако, ни одна из этих сил не сможет отрицать того, что современные экономические условия в нашей жизни стали намного сложнее. Принимать важные стратегические решения для общества и частных лиц стало труднее. Именно в моменты преодоления всех этих препятствий, появляется большой интерес к математическим методам, которые можно было бы применять в экономике, то есть к таким математическим методам, которые смогли бы выработать лучшую стратегию на решение действующих проблем и на долгосрочные проекты. Таким видом выхода из сложившейся ситуации стало решение задач в экономике при помощи матричных методов. На внедрение и развитие математических методов в решении экономических задач, большое влияние оказало создание и развитие современной вычислительной техники. Вычислительная техника нового поколения позволила применять на практике множество новых методов, которые были описаны ранее только в теории или объяснялись на простых примерах. Но никакая вычислительная техника не способна заменить человека и поэтому, люди должны уметь эффективно использовать теоретические знания в области математики в экономики. В нашем же случае, уметь правильно решать экономические задачи при помощи матричных методов.

собой математический объект, который записывается в формате прямоугольной таблицы с элементами внутри. Над матрицами можно осуществлять следующие операции:

1. равенство матриц;

4. умножение матриц на число;

5. умножение одной матрицы на другую матрицу.

Понятие матрицы и основанный на нем раздел математики — матричнаяалгебра — имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное — компактной матричной форме.

Из уроков математики мне известны основные операции над матрицами: равенство матриц; транспонирование; сложение и вычитание; умножение матрицы на число; умножение матрицы на матрицу.

Вообще, можно сказать, что матрица – это математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля. Рассмотрим пример:

Матричные методы находят широкое применение в экономической практике: сокращение документооборота, статистические расчёты, организация внутрипроизводственного хозрасчёта и для экономического анализа. Им пользуются при сравнении, при оценке структурных подразделений и работы самой организации в целом. Решая экономические задачи при помощи матричных методов, люди смогли решать основные задачи экономического типа на всех предприятиях и организациях.

Чтобы доказать это рассмотрим пример одной из экономических задач с помощью матриц:

Пусть фирма (Х) выпускает товары 3 видов ( , , ) и использует сыр 2-х видов ( , ), нормальный расход будет равен:

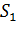
A =

С = (6070170). Стоимость единицы каждого вида сырья (денежных единиц) представлена матрицей: В =

Решая данную задачу аналитическим способом мы получаем, что затраты первого сырья будут равны: = 8*60 + 5*70+9*170 = 2360 единиц;

Затраты второго сырья будут равны: 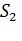= 6*60 + 8*70+4*170 = 1600 (единиц);

Следовательно, матрица затрат сырья S может быть записана следующим способом:

где S – это затраты на сырье; С – это заказ; A – это матрица производства.

Тогда: S = * (60 70170) = (2360 1600).

Общая стоимость сырья будет равна: Q= 2360*75+1600* 35= 233000.

Денежная единица может быть также записана и в матричном виде:

Q= S*B = (CA)B=(233000),

где Q – общая стоимость; B – стоимостью единицы сырья; а S – затраты на сырье.

Использование матриц в экономике не может происходить без матриц Абеля. Именно они позволяют рассмотреть нужную отрасль компании и привести ее к критериям выбора правильной конкурентоспособности.

Матричные методы можно также использовать для моделирования экономики отраслей народного хозяйства, экономики республик, народного хозяйства страны. Матрицы данного типа носят название межотраслевого баланса и находят широкое применение в планировании и статистике.

Исходя из этого, можно сделать вывод, что в экономической деятельности, в большей степени, используется метод анализа. Такой метод применяется для целей анализа сложных и многомерных экономических явлений. Чаще всего эти методы используются при необходимости сравнительной оценки функционирования организаций и их структурных подразделений. Следовательно, матричный метод в экономике – это метод научного исследования свойств объектов на основе использования правил теории матриц, по которым определяется значение элементов модели, отражающих взаимосвязи экономических объектов. Используется в тех случаях, когда главным объектом исследования являются балансовые соотношения затрат и результатов производственно-хозяйственной деятельности и нормативы затрат и выпусков. Рассмотрим на примере самое простое применение матрицы в отраслях экономики.

Ресурсы	Угольная промышленность	Здравоохранение
Электроэнергия	10,2	6,1
Трудовые ресурсы	7,8	3,5
Водные ресурсы	1,2

Упрощённая запись предложенных аналитических данных выглядит следующим образом:

Решение экономических задач, осуществляемое матричным методом, позволило решать основные задачи экономического профиля на любом из предприятий.

Пусть предприятие выпускает продукцию трёх видов ( , , ), использует сырьё двух типов ( , ), а нормы расхода.

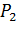
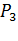
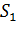
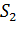
Стоимость единицы каждого типа сырья (ден. ед.) представлена матрицей-столбцом:

Эта задача решается аналитическим путем.

Поэтому матрица-строка затрат сырья S может быть записана как произведение, где S – затраты сырья; С – заказ; A – матрица производства.

Где общая стоимость сырья может быть записана в матричном виде, где Q – общая стоимость; B – стоимость единицы сырья; S – затраты сырья.

Применение матриц в экономике не может обойтись и без матрицы Абеля, т.к. она позволяет рассматриваемую отрасль какой-либо деятельности компании, привести к критериям выбора конкурентоспособности в технологиях синергетического эффекта и маркетинга.

ГЛАВА 2. МЕТОД ГАУССА.

прекрасно подходит для решения систем линейных алгебраических уравнений (СЛАУ). Он обладает рядом преимуществ по сравнению с другими методами:

· во-первых, нет необходимости предварительно исследовать систему уравнений на совместность;

· во-вторых, методом Гаусса можно решать не только СЛАУ, в которых число уравнений совпадает с количеством неизвестных переменных и основная матрица системы невырожденная, но и системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равен нулю;

· в-третьих, метод Гаусса приводит к результату при сравнительно небольшом количестве вычислительных операций.

Краткий обзор статьи.

Сначала дадим необходимые определения и введем обозначения.

Далее опишем алгоритм метода Гаусса для простейшего случая, то есть, для систем линейных алгебраических уравнений, количество уравнений в которых совпадает с количеством неизвестных переменных и определитель основной матрицы системы не равен нулю. При решении таких систем уравнений наиболее отчетливо видна суть метода Гаусса, которая заключается в последовательном исключении неизвестных переменных. Поэтому метод Гаусса также называют методом последовательного исключения неизвестных. Покажем подробные решения нескольких примеров.

В заключении рассмотрим решение методом Гаусса систем линейных алгебраических уравнений, основная матрица которых либо прямоугольная, либо вырожденная. Решение таких систем имеет некоторые особенности, которые мы подробно разберем на примерах.