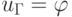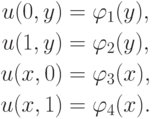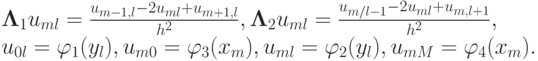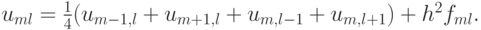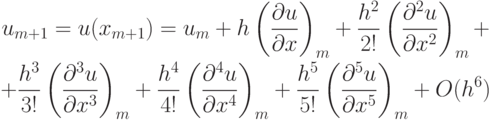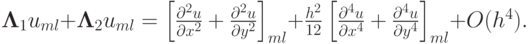Введение

Наиболее распространённым уравнением эллиптического типа является уравнение Пуассона.
К решению этого уравнения сводятся многие задачи математической физики, например задачи о стационарном распределении температуры в твердом теле, задачи диффузии, задачи о распределении электростатического поля в непроводящей среде при наличии электрических зарядов и многие другие.

Для решения эллиптических уравнений в случае нескольких измерений используют численные методы, позволяющие преобразовать дифференциальные уравнения или их системы в системы алгебраических уравнений. Точность решения опреде­ляется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера [1]

Цель публикации получить решение уравнения Пуассона для граничных условий Дирихле и Неймана, исследовать сходимость релаксационного метода решения на примерах.

Уравнение Пуассона относится к уравнениям эллиптического типа и в одномерном случае имеет вид [1]:

(1)

где x – координата; u(x) – искомая функция; A(x), f(x) – некоторые непрерывные функции координаты.

Видео:9. Уравнение ПуассонаСкачать

Решим одномерное уравнение Пуассона для случая А = 1, которое при этом принимает вид:

(2)

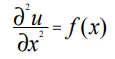
Зададим на отрезке [xmin, xmax] равномерную координатную сетку с шагом ∆х:

(3)

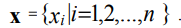
Граничные условия первого рода (условия Дирихле) для рассматривае­мой задачи могут быть представлены в виде:

(4)

где х1, xn – координаты граничных точек области [xmin, xmax]; g1, g2 – некоторые
константы.

Граничные условия второго рода (условия Неймана) для рассматривае­мой задачи могут быть представлены в виде:

(5)

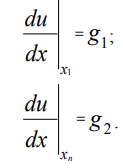
Проводя дискретизацию граничных условий Дирихле на равномерной координатной сетке (3) с использованием метода конечных разностей, по­лучим:

(6)

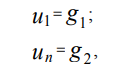
где u1, un – значения функции u(x) в точках x1, xn соответственно.

Видео:Решение уравнения Пуассона методом верхней релаксацииСкачать

Проводя дискретизацию граничных условий Неймана на сетке (3), по­лучим:

(7)

Проводя дискретизацию уравнения (2) для внутренних точек сетки, по­лучим:

(8)

где ui, fi – значения функций u(x), f(x) в точке сетки с координатой xi.

Таким образом, в результате дискретизации получим систему линейных алгебраических уравнений размерностью n, содержащую n – 2 уравнения вида (8) для внутренних точек области и уравнения (6) и (7) для двух граничных точек [1].

Ниже приведен листинг на Python численного решения уравнения (2) с граничными условиями (4) – (5) на координатной сетке (3).

Разработанная мною на Python программа удобна для анализа граничных условий.Приведенный алгоритм решения на Python использует функцию Numpy — u=linalg.solve(a,b.T).T для решения системы алгебраических уравнений, что повышает быстродействие при квадратной матрице . Однако при росте числа измерений необходимо переходить к использованию трех диагональной матрицы решение для которой усложняется даже для очень простой задачи, вот нашёл на форуме такой пример:

Программа численного решения на равномерной по каждому направлению сетки задачи Дирихле для уравнения конвекции-диффузии

(9)

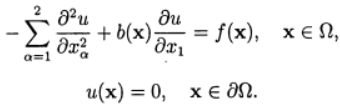
Используем аппроксимации центральными разностями для конвективного слагаемого и итерационный метод релаксации.для зависимость скорости сходимости от параметра релаксации при численном решении задачи с /(х) = 1 и 6(х) = 0,10. В сеточной задаче:

(10)

Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Представим матрицу А в виде суммы диагональной, нижней треугольной и верхней треугольных матриц:

(10)

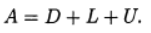
Метод релаксации соответствует использованию итерационного метода:

(11)

При говорят о верхней релаксации, при — о нижней релаксации.

На графике показана зависимость числа итераций от параметра релаксации для уравнения Пуассона (b(х) = 0) и уравнения конвекции-диффузии (b(х) = 10). Для сеточного уравнения Пуассона оптимальное значении параметра релаксации находится аналитически, а итерационный метод сходиться при .

1. Приведено решение эллиптической задачи на Python с гибкой системой установки граничных условий
2. Показано что метод релаксации имеет оптимальный диапазон () параметра релаксации.

Ссылки:

1. Рындин Е.А. Методы решения задач математической физики. – Таганрог:
   Изд-во ТРТУ, 2003. – 120 с.
2. Вабищевич П.Н.Численные методы: Вычислительный практикум. — М.: Книжный дом
   «ЛИБРОКОМ», 2010. — 320 с.

Уравнение Пуассона

Двумерное уравнение Пуассона — пример уравнения в частных производных эллиптического типа, включающее в себя вторые производные функции T(x,y) по двум пространственным переменным:
(1)

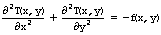
Уравнение Пуассона описывает, например, распределение электростатического поля T(x,y) в двумерной области с плотностью заряда f(x,y), или стационарное распределение температуры T(x,y) на плоскости, в которой имеются источники (или поглотители) тепла с интенсивностью f(x,y). Именно в последней физической интерпретации и будем далее рассматривать уравнение Пуассона (поэтому мы и обозначили искомую функцию символом T). Корректная постановка краевой задачи для уравнения Пуассона требует задания четырех (в двумерном случае) граничных условий.

Некоторые численные решения уравнения Пуассона с нулевыми граничными условиями и разными источниками показаны на рис.1-2.

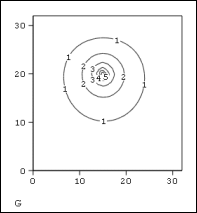
Рис.1. Решение уравнения Пуассона (график линий уровня) с одним источником и нулевыми граничными условиями

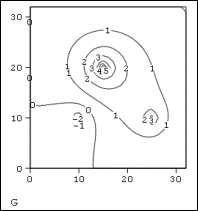
Рис.2. Решение уравнения Пуассона с тремя источниками разной интенсивности

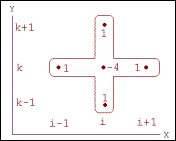
Согласно идеям метода сеток, уравнение Пуассона (1) может быть записано в разностной форме при помощи шаблона «крест» (рис.3). В этом случае, после приведения подобных слагаемых в разностных уравнениях коэффициенты разностной схемы будут такими, как показано возле узлов шаблона на этом рисунке (аналогичные коэффициенты для уравнения теплопроводности см. в описании метода сеток).

Рис.3. Шаблон аппроксимации схемы «крест» для уравнения Пуассона

Однако, в отличие от уравнения теплопроводности, разностная схема для уравнения Пуассона уже не может быть решена явно. Для ее реализации требуется решить систему линейных уравнений. Для ее решения можно использовать итерационный метод релаксации Якоби. Для его запуска требуется задать начальное приближение к решению (0-ю итерацию) и запустить итерационный процесс, уточняющий решение. Параметр численного алгоритма (число в пределах от 0 до 1) характеризует скорость сходимости итераций. Суть алгоритма релаксации сводится к тому, что в ходе итераций происходит проверка уравнений и соответствующая коррекция значений искомой функции в каждой точке. Если начальное приближение выбрано удачно, то можно надеяться, что алгоритм сойдется («срелаксирует») к правильному решению.

Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона

Видео:7.2 Задача 1. Краевая задача для уравнения ПуассонаСкачать

Среди всех типов уравнений математической физики эллиптические уравнения с точки зрения вычислителей стоят особняком. С одной стороны, имеется хорошо развитая теория решения эллиптических уравнений и систем. Достаточно легко доказываются теоремы об устойчивости разностных схем для эллиптических уравнений. Во многих случаях получаются априорные оценки точности расчетов и числа итераций при решении возникающих систем сеточных уравнений . С другой стороны, системы сеточных уравнений , возникающие при решении уравнений методами сеток, имеют большую размерность и плохо обусловлены. Для решения таких систем разработаны специальные итерационные методы .

6.1. Постановка задачи. Простейшая разностная схема «крест». Устойчивость схемы «крест»

Будем рассматривать двухмерное уравнение Пуассона

в единичном квадрате 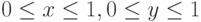с краевыми условиями первого рода на границе расчетной области

( — заданная на границе функция ).

В случае прямоугольной области граничные условия удобно записать в следующем виде:

Для простоты выкладок введем равномерную расчетную сетку с узлами <x_m, y_l> , m, l = 0, 1, . , M с равным количеством шагов по каждому пространственному направлению, сеточную область D — совокупность всех узлов сетки, включая граничные, и сеточную функцию < u_ml >. В этом случае шаги по координатам предполагаются равными. В случае неравных шагов по каждому направлению полученные результаты не изменятся, а запись уравнений станет более громоздкой.

Выбираем простейший пятиточечный шаблон разностной схемы «крест» . На этом шаблоне аппроксимирующее разностное уравнение легко выписать. Для этого производные заменим вторыми разностями:

где h — шаг по координатам, или в операторной форме

Эту же разностную схему можно записать в каноническом виде для разностных схем для эллиптических уравнений:

Видео:УМФ, 01.12, решение задач Лапласа и Пуассона в случае неоднородных граничных условийСкачать

Такую каноническую запись не следует путать с канонической формой записи итерационного метода, которая встретится ниже.

Такая схема обладает вторым порядком аппроксимации по обеим координатам. Это легко показать, применяя разложение в ряд Тейлора функции — проекции точного решения на сетку — вплоть до членов четвертого порядка включительно. Проведем такое разложение для одного из операторов, стоящих в данном разностном уравнении:

Здесь учтено разложение проекции точного решения в ряд Тейлора

и аналогичное разложение для u_{m — 1}.

Для рассматриваемого двухмерного уравнения получим выражение для главного члена невязки

Рассмотрим устойчивость полученной схемы. Отметим, что методы исследования на устойчивость , применяемые для эволюционных (зависящих от времени) уравнений, здесь не работают. Действовать приходится на основе определения устойчивости.

Сформулируем и докажем две леммы, которые облегчат процедуру доказательства устойчивости разностной схемы.

Видео:Практическое занятие. Численное решение уравнений Лапласа и ПуассонаСкачать

💡 Видео

Кобельков Г. М. - Численные методы. Часть 2 - Численные методы для эллиптических уравненийСкачать

ЧК_МИФ_3_1_2_5 (L3) УРАВНЕНИЕ ПУАССОНАСкачать

Формула ГринаСкачать

Стрим с Борисом Надеждиным, Екатериной Дунцовой и Дмитрием КисиевымСкачать

Физика. Связь напряженности и потенциалаСкачать

Билет №04 "Потенциал электростатического поля"Скачать

Задача Дирихле для круга. Уравнение ЛапласаСкачать

ЧК МИФ 3 1 3 3 5 L4 Уравнение ПуассонаСкачать

6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать

УМФ, 08.12, уравнения Лапласа и Пуассона для кругаСкачать

Шар заряд.Уравнение ПуассонаСкачать

ЗАДАЧА на электростатическое поле │Расчет плоского конденсатора │Уравнение ПуассонаСкачать

6-2. Метод сетокСкачать