Решение дробных уравнений с заменой переменной

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Научиться решать дробно-рациональные уравнения методом введения переменной.

Научиться определять ту часть уравнения, которую нужно обозначить через новую переменную.

Решить получившееся дробно-рациональное уравнение.

Отобрать корни, которые не обращают знаменатель в ноль.

Найти корни исходного уравнения, используя значения

Тип урока: урок открытия нового знания.

Познавательные: анализировать, делать выводы, сравнивать объекты по способам действий.

Регулятивные: определять цель, проблему, выдвигать версии, планировать деятельность.

Коммуникативные: излагать свое мнение, использовать речевые средства,

Личностные: осознавать свои эмоции, вырабатывать уважительное отношение к одноклассникам.

Предметные: умение на выполнении задания построить алгоритм для решения уравнений каждого вида.

Метапредметные : умение выдвигать гипотезы, предположения, видеть различные способы решения задачи.

Личностные: умение правильно излагать свои мысли, понимать смысл поставленной задачи

Учебник, компьютер, проектор, презентация, карточки для творческого задания и самостоятельной работы.

Организационный момент. Приветствие. Проверка наличия всех нужных учебных пособий для урока

Какие дроби называются взаимно обратными?

Что называется уравнением?

Какие уравнения называются целыми?

Какие уравнения называются дробными рациональными?

Что значит решить уравнение?

Составьте алгоритм решения дробного рационального уравнения .

Найдите общий знаменатель дробей

а)

б)

в)

г)

Способы решения дробных рациональных уравнений.

а) ;

б) ;

в) ;

г) .

На основании материала устной работы учащиеся формулируют тему, цель и задачи урока.

Тема урока: Решение дробных рациональных уравнений методом введения новой переменной.

Цель урока: Научиться решать дробные рациональные уравнения методом введения новой переменной.

Научиться определять ту часть уравнения, которую нужно обозначить через новую переменную.

Решить получившееся дробно-рациональное уравнение.

Отобрать корни, которые не обращают знаменатель в ноль.

Найти корни исходного уравнения, используя значения введенной переменной.

Постановка проблемной ситуации.

Решите уравнение:

— Попробуем решить данное уравнение, согласно алгоритма решения дробных рациональных уравнений.

Найдем общий знаменатель;

Найдем дополнительные множители для каждой из дробей;

Попробуем решить получившееся целое уравнение.

Решают уравнение с помощью учебника.

В учебнике рассмотрен способ решения данного уравнения методом введения новой переменной, потому что при решении данного уравнения с помощью общего алгоритма решения дробно-рациональных уравнений получается уравнение высших степеней.

Решение заданий № 297(а) и уравнение вида

1) Решение задания № 297(а).

Введем новую переменную. Пусть .

; (ф. Виета)

После нахождения значения введенной переменной решаем исходное уравнение:

1) — нет корней.

2)

2) Решение уравнения:

Введем новую переменную. Пусть .

; (ф. Виета)

После нахождения значения введенной переменной решаем исходное уравнение:

1)

— нет корней.

Видео для физминутки.

Самостоятельная работа с самопроверкой.

а) ;

б)

а) ;

б)

Ответы к самостоятельной работе.

б) 2; 5; ; .

п. 13; № 297 (в); № 298 (б). Дополнительно: № 300 (б).

Что вы нового узнали на уроке?

Как мы решали поставленные задачи?

Что мы для этого использовали?

Что вы еще хотите для себя узнать нового на следующих уроках?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 925 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 684 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Дробные рациональные уравнения (способ замены переменной)Скачать

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 576 030 материалов в базе

Материал подходит для УМК

«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.

13. Дробные рациональные уравнения

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 14.12.2019
• 331
• 4

• 27.02.2019
• 1067
• 75

• 06.02.2019
• 596
• 3

• 26.01.2019
• 1544
• 31

• 23.01.2019
• 1523
• 80

• 21.01.2019
• 857
• 18

• 13.01.2019
• 1076
• 8

• 09.01.2019
• 1113
• 8

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 22.01.2020 1313
• DOCX 142.5 кбайт
• 28 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Федив Юлия Ивановна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 8 месяцев
• Подписчики: 1
• Всего просмотров: 22785
• Всего материалов: 16

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Зачётный способ решить дробно рациональное уравнение методом заменыСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Приемная кампания в вузах начнется 20 июня

Время чтения: 1 минута

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

Время чтения: 2 минуты

Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.

Время чтения: 2 минуты

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Решение уравнений с переменной в знаменателе дроби

Вы будете перенаправлены на Автор24

Уравнения, содержащие переменную в знаменателе можно решать двумя способами:

Приведя дроби к общему знаменателю

Используя основное свойство пропорции

Вне зависимости от выбранного способа необходимо после нахождения корней уравнения выбрать из найденных допустимые значения, т.е те, которые не обращают знаменатель в $0$.

Видео:Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

1 способ. Приведение дробей к общему знаменателю.

Решение:

1.Перенесем дробь из правой части уравнения в левую

Для того чтобы правильно это сделать, вспомним, что при перенесении элементов в другую часть уравнения меняется знак перед выражениями на противоположный. Значит, если в правой части перед дробью был знак «+», то в левой перед ней будет знак «-».Тогда в левой части получим разность дробей.

2.Теперь отметим что у дробей разные знаменатели, значит для того, чтобы составить разность необходимо привести дроби к общему знаменателю. Общим знаменателем будет произведение многочленов, стоящих в знаменателях исходных дробей: $(2x-1)(x+3)$

Для того чтобы получить тождественное выражение, числитель и знаменатель первой дроби необходимо умножить на многочлен $(x+3)$, а второй на многочлен $(2x-1)$.

Выполним преобразование в числителе первой дроби-произведем умножение многочленов. Вспомним , что для этого необходимо умножить первое слагаемое первого многочлена умножить на каждое слагаемое второго многочлена, затем второе слагаемое первого многочлена умножить на каждое слагаемое второго многочлена и результаты сложить

[left(2x+3right)left(х+3right)=2хcdot х+2хcdot 3+3cdot х+3cdot 3=^2+6х+3х+9]

Приведем подобные слагаемые в полученном выражении

[left(2x+3right)left(х+3right)=2хcdot х+2хcdot 3+3cdot х+3cdot 3=^2+6х+3х+9=] [^2+9х+9]

Выполним аналогично преобразование в числителе второй дроби-произведем умножение многочленов

$left(x-5right)left(2х-1right)=хcdot 2х-хcdot 1-5cdot 2х+5cdot 1=^2-х-10х+5=^2-11х+5$

Тогда уравнение примет вид:

Теперь дроби с одинаковым знаменателем, значит можно производить вычитание. Вспомним, что при вычитании дробей с одинаковым знаменателем из числителя первой дроби необходимо вычесть числитель второй дроби, знаменатель оставить прежним

Преобразуем выражение в числителе. Для того, чтобы раскрыть скобки, перед которыми стоит знак «-» надо изменить все знаки перед слагаемыми , стоящими в скобках на противоположные

Приведем подобные слагаемые

Тогда дробь примет вид

3.Дробь равна $0$, если ее числитель равен 0. Поэтому мы приравниваем числитель дроби к $0$.

Решим линейное уравнение:

4.Проведем выборку корней. Это значит, что необходимо проверить, не обращаются ли знаменатели исходных дробей в $0$ при найденных корнях.

Поставим условие, что знаменатели не равны $0$

Значит допустимы все значения переменных, кроме $-3$ и $0,5$.

Найденный нами корень является допустимым значением, значит его смело можно считать корнем уравнения. Если бы найденный корень был бы не допустимым значением, то такой корень был бы посторонним и ,конечно, не был бы включен в ответ.

Ответ:$-0,2.$

Теперь можем составить алгоритм решения уравнения, которое содержит переменную в знаменателе

Видео:Решение уравнения методом замены переменнойСкачать

Алгоритм решения уравнения, которое содержит переменную в знаменателе

Перенести все элементы из правой части уравнения в левую. Для получения тождественного уравнения необходимо изменить все знаки, стоящие перед выражениями в правой части на противоположные

Если в левой части мы получим выражение с разными знаменателями, то приводим их к общему, используя основное свойство дроби. Выполнить преобразования, используя тождественные преобразования и получить итоговую дробь равную $0$.

Приравнять числитель к $0$ и найти корни получившегося уравнения.

Проведем выборку корней, т.е. найти допустимые значения переменных, которые не обращают знаменатель в $0$.

Видео:#138 Урок 63. Решение дробно-рациональных уравнений методом замены переменной. Алгебра 8 класс.Скачать

2 способ. Используем основное свойство пропорции

Основным свойством пропорции является то, что произведение крайних членов пропорции равно произведению средних членов.

Используем данное свойство для решения этого задания

1.Найдем и приравняем произведение крайних и средних членов пропорции.

Решив полученное уравнение, мы найдем корни исходного

2.Найдем допустимые значения переменной .

Из предыдущего решения (1 способ) мы уже нашли , что допустимы любые значения, кроме $-3$ и $0,5$.

Тогда, установив что найденный корень является допустимым значением, мы выяснили, что $-0,2$ будет являться корнем.

Ответ:$-0,2.$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 12 05 2021

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Урок 1. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.

Решение уравнений, приводящихся к квадратным. Биквадратные уравнения. Замена переменной в уравнениях. Какое уравнение является биквадратным. Определение биквадратного уравнения. Как решать биквадратное уравнение. Как найти корни биквадратного уравнения. Уравнения, приводящиеся к квадратным путем замены переменной. Квадратные уравнения. Алгебра 8 класс. Примеры с решением.

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Урок 2. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.

Биквадратные уравнения. Уравнения 4-й степени. Замена переменной в уравнениях. Решение уравнений, приводящихся к квадратным, путем замены переменной. Какое уравнение является биквадратным. Определение биквадратного уравнения. Как решать биквадратное уравнение. Как найти корни биквадратного уравнения. Алгебра 8 класс. Примеры с решением.

Урок 3. Замена переменной. Решение уравнений, приводящихся к квадратным. Алгебра 8 класс.

Решение уравнений, приводящихся к квадратным путем замены. Алгебра 8 класс. Замена переменной в уравнениях. Примеры с решением.

Урок 4. Замена переменной в уравнениях, приводящихся к квадратным.

Решение уравнений, приводящихся к квадратным путем замены. Алгебра 8 класс. Замена переменной в уравнениях. Примеры с решением.

Пример 1: Решите уравнение методом замены переменной:

Если необходимо решить уравнение вида (x+A)(x+B)(x+C)(x+D) = m где А, В, С, D и m — некоторые константы, то группируем попарно скобки таким образом, чтобы была равна сумма констант, входящих в эти скобки.

Например, если А+D = В+C, то записываем: (x+A)(x+D)(x+B)(x+C) = m

• Попарно раскрываем скобки: (x2+Ax+Dх + AD)(x2+Bx+Cх +DC) = m (x2+(A+D)х + AD)(x2+(B+C)х + DC) = m
• Делаем замену x2+(A+D)х = t Получаем уравнение (t + AD)(t + DC) = m
• После раскрытия скобок получим обычное квадратное уравнение.

Урок 5. Решение дробно-рациональных уравнений методом замены.

Решение дробно-рациональных уравнений методом замены. Алгебра 8 класс. Как сделать замену в дробно-рациональном уравнении? Решение рационального уравнения заменой. Обратные числа. Какие числа называются взаимно обратными? Взаимно-обратные дроби. Как правильно сделать замену взаимно-обратных дробей. Примеры с решением. Задания с объяснением.

Урок 6. Решение дробно-рациональных уравнений методом замены переменной. Алгебра 8 класс.

Решение дробно-рациональных уравнений методом замены. Задания с *. Алгебра 8 класс. Как сделать замену в дробно-рациональном уравнении? Как правильно возвести в квадрат при замене переменной. Как определить что заменять и какую замену делать. Решение рационального уравнения заменой. Примеры с решением. Задания с объяснением.

Урок 7. Решение уравнений методом замены. Как понизить степень уравнения заменив переменную?

Решение дробно-рациональных уравнений методом замены. Как понизить степень уравнения заменив переменную? Задания с *. Алгебра 8 класс. Как сделать замену в рациональном уравнении? Уравнения 4-й степени. Понизить степень уравнения, сделав замену. Как определить что заменять и какую замену делать. Решение рационального уравнения заменой. Примеры с решением. Задания с объяснением.

Урок 8. Замена переменной. Решение уравнений. Однородные уравнения.

Однородные уравнения второй степени. Определение однородного уравнения. Методы решения однородных уравнений. Как понять, что уравнение однородное. Решение однородных уравнений методом замены переменной. Решение уравнений методом замены переменной. Решить уравнение. Решить заменой. Примеры с решением. Задания с объяснением. Алгебра 8 класс.

📸 Видео

ЭТО НУЖНО ЗНАТЬ — Как решать Дробно Рациональные уравнения?Скачать

решение уравнения с заменой переменнойСкачать

Алгебра 9 класс. Решение систем уравнений методом замены переменныхСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

8 класс "Решение уравнений методом замены переменной"Скачать

#137 Урок 62. Решение дробно-рациональных уравнений методом замены. Алгебра 8 класс. Математика.Скачать

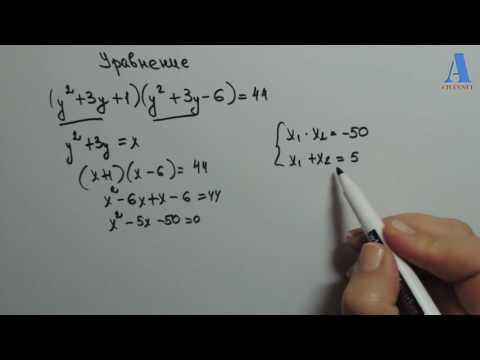
Как решают уравнения в России и СШАСкачать

9 класс. Алгебра. Решение уравнений методом замены переменной.Скачать

Алгебра Система уравнений Метод замены переменной № 6.22 9 классСкачать

Решение уравнений методом замены переменной.Скачать

Удобная замена переменной ➜ Быстрый способ решенияСкачать

Алгебра 8 класс : Решение уравнений с помощью заменыСкачать