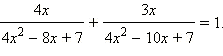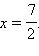В этой статье я покажу вам алгоритмы решения семи типов рациональных уравнений, которые с помощью замены переменных сводятся к квадратным. В большинстве случаев преобразования, которые приводят к замене, весьма нетривиальны, и самостоятельно о них догадаться достаточно трудно.
Для каждого типа уравнений я объясню, как в нем делать замену переменной, а затем в соответствующем видеоуроке покажу подробное решение.
У вас есть возможность продолжить решение уравнений самостоятельно, а затем сверить свое решение с видеоуроком.
1 . (x-1)(x-7)(x-4)(x+2)=40
Заметим, что в левой части уравнения стоит произведение четырех скобок, а в правой — число.
1. Сгруппируем скобки по две так, чтобы сумма свободных членов была одинаковой.
2. Перемножим их.
3. Введем замену переменной.
В нашем уравнении сгруппируем первую скобку с третьей, а вторую с четвертой,так как (-1)+(-4)=(-7)+2:
В этом месте замена переменной становится очевидной:
Получаем уравнение
Ответ:
2 .
Уравнение этого типа похоже на предыдущее с одним отличием: в правой части уравнения стоит произведение числа на 
1. Группируем скобки по две так, чтобы произведение свободных членов было одинаковым.
2. Перемножаем каждую пару скобок.
3. Из каждого множителя выносим за скобку х.
4. Делим обе части уравнения на 
5. Вводим замену переменной.
В этом уравнении сгруппируем первую скобку с четвертой, а вторую с третьей, так как 
Заметим, что в каждой скобке коэффициент при 

Так как х=0 не является корнем исходного уравнения, разделим обе части уравнения на 
Теперь можем ввести замену переменной:
Получим уравнение:
Ответ:
3 .
Заметим, что в знаменателях обоих дробей стоят квадратные трехчлены, у которых старший коэффициент и свободный член одинаковые. Вынесем, как и в уравнении второго типа х за скобку. Получим:
Разделим числитель и знаменатель каждой дроби на х:
Теперь можем ввести замену переменной:
Получим уравнение относительно переменной t:
Ответ:
4 .
Заметим, что коэффициенты уравнения симметричны относительно центрального. Такое уравнение называется возвратным .
Чтобы его решить,
1. Разделим обе части уравнения на 
2. Сгруппируем слагаемые таким образом:
3. В каждой группе вынесем за скобку общий множитель:
4. Введем замену:
5. Выразим через t выражение 
Отсюда
Получим уравнение относительно t:
Ответ:
5. Однородные уравнения.
Уравнения, имеющие структуру однородного, могут встретиться при решении показательных, логарифмических и тригонометрических уравнений, поэтому ее нужно уметь распознавать.
Однородные уравнения имеют такую структуру:
В этом равенстве А, В и С — числа, а квадратиком и кружочком обозначены одинаковые выражения. То есть в левой части однородного уравнения стоит сумма одночленов, имеющих одинаковую степень ( в данном случае степень одночленов равна 2), и свободный член отсутствует.
Чтобы решить однородное уравнение, разделим обе части на
Или на
Или на
Внимание! При делении правой и левой части уравнения на выражение, содержащее неизвестное, можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.
Пойдем первым путем. Получим уравнение:

Теперь мы вводим замену переменной:


При решении уравнения я обычно придерживаюсь такой тактики: нужно уменьшить количество различных выражений, в состав которых входит неизвестное ( принцип «бритвы Оккама» — не нужно множить сущности без нужды), а для этого помогает разложить выражения с неизвестным на множители. Разложим выражение, стоящее в правой части уравнения на множители.
Перенесем все влево, получим:
Теперь мы видим, что перед нами однородное уравнение. Разделим обе части уравнения на 
Теперь самое время ввести замену переменной:
Получим квадратное уравнение:
Ответ:
6 .
Это уравнение имеет такую структуру:




Теперь возведем каждую скобку в четвертую степень, используя треугольник Паскаля:
Упростим выражение и получим биквадратное уравнение относительно t:
Ответ: 
7 .
Это уравнение имеет такую структуру:
Чтобы его решить, нужно в левой части уравнения выделить полный квадрат.
Чтобы выделить полный квдарат, нужно прибавить или вычесть удовоенное произведение. Тогда мы получим квадрат суммы ли разности. Для удачной замены переменной это имеет определяющее значение.
Начнем с нахождения удвоенного произведения. Именно оно будет ключиком для замены переменной. В нашем уравнении удвоенное произведение равно
Теперь прикинем, что нам удобнее иметь — квадрат суммы или разности. Рассмотрим, для начала сумму выражений:
Отлично! это выражении в точности равно удвоенному произведению. Тогда, чтобы в скобках получить квадрат суммы, нужно прибавить и вычесть удвоенное произведение:

Введем замену:
Получим квадратное уравнение:
Ответ:
- Урок 1. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.
- Урок 2. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.
- Урок 3. Замена переменной. Решение уравнений, приводящихся к квадратным. Алгебра 8 класс.
- Урок 4. Замена переменной в уравнениях, приводящихся к квадратным.
- Решение дробно рациональных уравнений с заменой
- 📺 Видео
Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Урок 1. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.
Решение уравнений, приводящихся к квадратным. Биквадратные уравнения. Замена переменной в уравнениях. Какое уравнение является биквадратным. Определение биквадратного уравнения. Как решать биквадратное уравнение. Как найти корни биквадратного уравнения. Уравнения, приводящиеся к квадратным путем замены переменной. Квадратные уравнения. Алгебра 8 класс. Примеры с решением.
Видео:Зачётный способ решить дробно рациональное уравнение методом заменыСкачать

Урок 2. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.
Биквадратные уравнения. Уравнения 4-й степени. Замена переменной в уравнениях. Решение уравнений, приводящихся к квадратным, путем замены переменной. Какое уравнение является биквадратным. Определение биквадратного уравнения. Как решать биквадратное уравнение. Как найти корни биквадратного уравнения. Алгебра 8 класс. Примеры с решением.
Урок 3. Замена переменной. Решение уравнений, приводящихся к квадратным. Алгебра 8 класс.
Решение уравнений, приводящихся к квадратным путем замены. Алгебра 8 класс. Замена переменной в уравнениях. Примеры с решением.
Урок 4. Замена переменной в уравнениях, приводящихся к квадратным.
Решение уравнений, приводящихся к квадратным путем замены. Алгебра 8 класс. Замена переменной в уравнениях. Примеры с решением.
Пример 1: Решите уравнение методом замены переменной:
Если необходимо решить уравнение вида (x+A)(x+B)(x+C)(x+D) = m где А, В, С, D и m — некоторые константы, то группируем попарно скобки таким образом, чтобы была равна сумма констант, входящих в эти скобки.
Например, если А+D = В+C, то записываем: (x+A)(x+D)(x+B)(x+C) = m
- Попарно раскрываем скобки: (x2+Ax+Dх + AD)(x2+Bx+Cх +DC) = m (x2+(A+D)х + AD)(x2+(B+C)х + DC) = m
- Делаем замену x2+(A+D)х = t Получаем уравнение (t + AD)(t + DC) = m
- После раскрытия скобок получим обычное квадратное уравнение.
Урок 5. Решение дробно-рациональных уравнений методом замены.
Решение дробно-рациональных уравнений методом замены. Алгебра 8 класс. Как сделать замену в дробно-рациональном уравнении? Решение рационального уравнения заменой. Обратные числа. Какие числа называются взаимно обратными? Взаимно-обратные дроби. Как правильно сделать замену взаимно-обратных дробей. Примеры с решением. Задания с объяснением.
Урок 6. Решение дробно-рациональных уравнений методом замены переменной. Алгебра 8 класс.
Решение дробно-рациональных уравнений методом замены. Задания с *. Алгебра 8 класс. Как сделать замену в дробно-рациональном уравнении? Как правильно возвести в квадрат при замене переменной. Как определить что заменять и какую замену делать. Решение рационального уравнения заменой. Примеры с решением. Задания с объяснением.
Урок 7. Решение уравнений методом замены. Как понизить степень уравнения заменив переменную?
Решение дробно-рациональных уравнений методом замены. Как понизить степень уравнения заменив переменную? Задания с *. Алгебра 8 класс. Как сделать замену в рациональном уравнении? Уравнения 4-й степени. Понизить степень уравнения, сделав замену. Как определить что заменять и какую замену делать. Решение рационального уравнения заменой. Примеры с решением. Задания с объяснением.
Урок 8. Замена переменной. Решение уравнений. Однородные уравнения.
Однородные уравнения второй степени. Определение однородного уравнения. Методы решения однородных уравнений. Как понять, что уравнение однородное. Решение однородных уравнений методом замены переменной. Решение уравнений методом замены переменной. Решить уравнение. Решить заменой. Примеры с решением. Задания с объяснением. Алгебра 8 класс.
Видео:Дробные рациональные уравнения (способ замены переменной)Скачать

Решение дробно рациональных уравнений с заменой
Пожалуй, самым важным методом решения уравнений любого типа является введение нового неизвестного, относительно которого уравнение имеет более простой вид, легко приводящийся к элементарному типу.
Перечислим наиболее часто встречающиеся типы замен.
Замена ( степенная замена )
В частности, с помощью замены так называемое биквадратное уравнение приводится к квадратному.
Замена 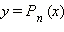
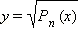
Чаще всего встречается замена 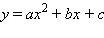
Замена 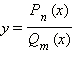
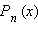
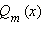
В частности, с помощью широко распространённой замены 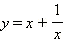
Покажем, как это делается. Так как , то число не является корнем этого уравнения. Разделим уравнение на , получим
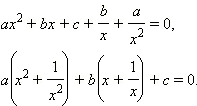 |
А так как 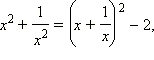
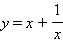
Дадим два практических совета.
Совет 1. Замену переменных нужно делать сразу, при первой же возможности.
Совет 2. Уравнение относительно новой переменной нужно решать до конца, и лишь затем возвращаться к старому неизвестному.
Сделаем замену переменных 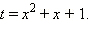
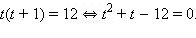
1) 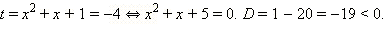
2) 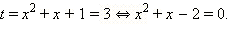
Решите уравнение
Непосредственной проверкой убеждаемся, что не является корнем этого уравнения. Разделим числитель и знаменатель каждой из дробей на . Имеем
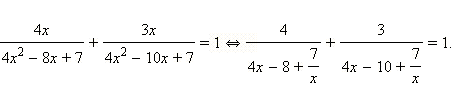
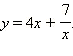
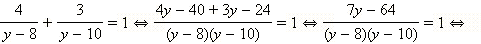 |
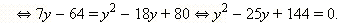 |
Корни этого уравнения и . Имеем два случая:
1) 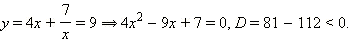
2) 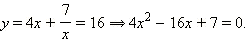
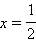
Ответ. 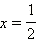
📺 Видео
Дробно-рациональные уравнения. 8 класс.Скачать

ЭТО НУЖНО ЗНАТЬ — Как решать Дробно Рациональные уравнения?Скачать

Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

№6 Дробно-рациональные уравнения. Замена переменной.Скачать

ЕГЭ задание 12 Дробно рациональное уравнение Метод заменыСкачать

№3 Дробно-рациональные уравнения. Замена переменной.Скачать

№7 Дробно-рациональные уравнения. Замена переменной.Скачать

Решение рациональных уравнений заменой переменных.Скачать

№8 Дробно-рациональные уравнения. Замена переменной.Скачать

Рациональные уравнения. ОГЭ номер 21 | ЕГЭ номер 13 | Математика | TutorOnlineСкачать

№4 Дробно-рациональные уравнения. Замена переменной.Скачать

Решение уравнения методом замены переменнойСкачать

#138 Урок 63. Решение дробно-рациональных уравнений методом замены переменной. Алгебра 8 класс.Скачать

Решение дробных рациональных уравнений. Алгебра, 8 классСкачать

#137 Урок 62. Решение дробно-рациональных уравнений методом замены. Алгебра 8 класс. Математика.Скачать

Замена переменной. Рациональные уравнения Часть 2 из 4Скачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать