В дальнейшем будут использоваться следующие обозначения:
N = — множество натуральных чисел;
N * = — множество натуральных положительных чисел;
Z = — — множество целых чисел;
Q = < m /n | m Î Z, n Î N * > — множество рациональных чисел;
R — множество действительных (вещественных) чисел.
В начале представим некоторые определения и утверждения, необходимые для далнейшего изложения
Определение. Пусть a,b Î Z, b ≠ 0. Числа q Î Z и r Î <0,1. |b|-1> называются соответственно неполным частным и остатком от деления a на b, если выполнено равенство
| a = bq + r. | (1) |
При этом, если r = 0, то говорят, что a делится на b, или что b делит a, или что b является делителем a (обозначение a 
b или b|a.
Доказывается, что для любых целых чисел a, b; b ≠ 0, существуют единственные целые числа q, r, r Î <0. |b| — 1> такие, что имеет место соотношение (1).
Определение. Наименьшим общим кратным ненулевых целых чисел a1, a2, . an называется наименьшее положительное число, которое делится на каждое из этих чисел (обозначение [a1, a2, . an]).
Определение. Наибольшим общим делителем целых чисел a1, a2, . an, из которых хотя бы одно отлично от нуля, называется наибольшее натуральное число, на которое делится каждое из этих чисел (обозначение (a1, a2, . an)).
Определение. Числа a,b Î Z называются взаимно простыми, если (a,b) = 1.
Определение. Пусть даны числа a,b Î Z, причем c ≠ 0. Говорят, что число a сравнимо с числом b по модулю c, (обозначение a ≡ b (mod c)), если c|a — b; в противном случае говорят, что число a не сравнимо с числом b по модулю c (обозначение a 
b(mod c)).
Определение. Натуральное положительное число, большее 1 и не имеющее натуральных положительных делителей, отличных от 1 и самого себя, называется постым. Остальные натуральные числа, большие 1, называются составными. Число 1 не является ни простым, ни составным.
Основная теорема арифметики.
Всякое натуральное число, большее 1, разлагается в произведение простых чисел (не обязательно различных), причем указанное разложение единственно с точностью до порядка следования множителей.
Малая теорема Ферма.
Пусть p — простое число. Тогда для любого целого числа a справедливо соотношение a p ≡ a(mod p).
О диофантовом анализе
При исследовании диофантовых уравнений обычно ставятся следующие вопросы:
- имеет ли уравнение целочисленные решения;
- конечно или бесконечно множество его целочисленных решений;
- решить уравнение на множестве целых чисел, т. е. найти все его целочисленные решения;
- решить уравнение на множестве целых положительных чисел;
- решить уравнение на множестве рациональных чисел.
Отметим, что проблема решения уравнений в целых числах решена до конца только для уравнений с одним неизвестным, для уравнений первой степени и для уравнений второй степени с двумя неизвестными. Для уравнений выше второй степени с двумя или более неизвестными достаточно трудной является даже задача существования целочисленных решений. Например, не известно, имеет ли уравнение x 3 + y 3 + z 3 = 30 хотя бы одно целочисленное решение. Более того, доказано, что в принципе не существует единого алгоритма, позволяющего за конечное число шагов решать в целых числах произвольные диафантовы уравнения.
Диофантовы уравнения с одним неизвестным
Рассмотрим уравнение
| a0 + a1x + . + anx n = 0, | (2) |
где aj Î Z ( j = 0. n), an ≠ 0.
Покажем, каким образом можно определить все рациональные корни уравнения (2) (этот метод позволяет, в частности, решать уравнения вида (2) в целых числах). Не нарушая общности рассуждений, можно считать, что a0 ≠ 0. Пусть r — рациональный корень уравнения (2), r = p /q, где p Î Z, q Î N * , (p,q) = 1. Умножая обе части равенства 
на q n , получим a0q n + a1p·q n-1 + . + an-1p n-1 q + anp n = 0, следовательно,
| p|a0q n и q|anp n . | (3) |
Так как (p,q) = 1, то (p,q n ) = 1, (q,p n ) = 1, поэтому из соотношений (3) следует, что p|a0, q|an. Поскольку рациональных чисел вида r = p /q, таких что (p,q) = 1, p|a0, q|an, конечное число, то за конечное число шагов можно выбрать те из них, которые являются решением уравнения (2). Как следует из приведенных выше рассуждений, других решений уравнение (2) иметь не может.
Задача 1. Решить в рациональных числах уравнение
| 2x 4 + 7x 3 — 12x 2 — 38x + 21 = 0. | (4) |
Решение. Свободный член уравнения имеет следующие делители ±1, ±3, ±7, ±21. Выпишем также положительные делители старшего коэффициента: 1, 2. Следовательно, для рационального корня уравнения (4) получаем следующие возможные значения: 
Подстановкой в исходное уравнение убеждаемся, что из этого множества только числа -3 и 1 /2 являются его корнями.
Задача 2. Решить в целых числах уравнение
| x 8 + x 7 + x + 1 = 0. | (5) |
Решение. Делители свободного члена уравнения: ±1. Положительные делители старшего коэффициента: 1. Следовательно, все целые корни уравнения (5) находятся среди чисел . Подставляя x = ±1 в (5) заключаем, что только x = -1 является корнем этого уравнения.
Диофантовы уравнения первой степени
Перейдем теперь к решению в целых числах уравнений первой степени или так называемых линейных уравнений, т. е. уравнений вида
| a1x1 + a2x2 + . + anxn = b, | (6) |
где aj Î Z (j = 1,2. n), b Î Z.
Предположим, что не все числа aj (j = 1. n) равны нулю. Очевидно, для существования решения в целых числах уравнения (6) необходимо, чтобы (a1. an)|b. Покажем, что это условие является и достаточным.
Положив 
перейдем к равносильному уравнению
| a1 ¢ x1 + . + an ¢ xn = b ¢ , | (7) |
где (a1 ¢ , . an ¢ ) = 1. Пусть ai ¢ , aj ¢ — два ненулевых числа, таких, что |ai ¢ | ≠ |aj ¢ |. Для определенности предположим, что i ¢ | > |aj ¢ |. Разделив с остатком ai ¢ на aj ¢ , получим представление ai ¢ = aj ¢ q + r. Заменив ai ¢ на aj ¢ q + r в уравнении (7), приведем его к виду
| a1 ¢ x1 + . + rxi + . + aj ¢ (xj + qxi) + . + an ¢ xn = b ¢ . | (8) |
Перепишем уравнение (8) в виде
| a1 ¢ ¢ x1 + . + an ¢ ¢ xn ¢ ¢ = b ¢ , | (9) |
где
| ak ¢ ¢ = |
| , | xk ¢ ¢ = |
Очевидно, что решения уравнения (7) и (9). связаны между собой взаимно однозначным соответствием и, таким образом, решив уравнение (9), несложно найти все решения уравнения (7). С другой стороны отметим, что » k, i Î <1. n>, k ≠ i ak ¢ ¢ = ak ¢ , |ai ¢ ¢ | ¢ |. Следовательно, за конечное число шагов уравнение (7) приведется к виду
где числа Задача 3. Решить в целых числах уравнение 4x — 6y + 11z = 7. Решение. Разделив с остатком -6 на 4, получим -6 = 4(-2) + 2. Представим исходное уравнение в виде 4(x — 2y) + 2y + 11z = 7. После замены x ¢ = x — 2y это уравнение запишется следующим образом 4x ¢ + 2y + 11z = 7. Учитывая, что 11 = 2·5 + 1, преобразуем последнее уравнение: 4x ¢ + 2(y + 5z) + z = 7. Положив y ¢ = y + 5z, получим 4x ¢ + 2y ¢ + z = 7. Это уравнение имеет следующее решение: x ¢ , y ¢ — произвольные целые числа, z = 7 — 4x ¢ — 2y ¢ . Следовательно y = y ¢ — 5z = 20x ¢ + 11y ¢ — 35, x = x ¢ + 2y = 41x ¢ + 22y ¢ — 70. Таким образом, решение исходного уравнения имеет вид
где x ¢ , y ¢ — произвольные целые числа. Диофантовы уравнения высших степеней 1. Метод разложения на множители Задача 4. Решить в целых числах уравнение x + y = xy. Решение. Запишем уравнение в виде (x — 1)(y — 1) = 1. Произведение двух целых чисел может равняться 1 только в том случае, когда оба они равны 1. Т. е. исходное уравнение равносильно совокупности
с решениями (0,0) и (2,2). Задача 5. Доказать, что уравнение x 5 + 3x 4 y — 5x 3 y 2 — 15x 2 y 3 + 4xy 4 + 15y 5 = 33 неразрешимо в целых числах. Решение. Левая часть уравнения разлагается на множители следующим образом: (x — 2y)(x — y)(x + y)(x + 2y)(x + 3y). Если y ≠ 0, то в этом выражении все 5 множителей различны. С другой стороны, число 33 можно разделить максимум на 4 различных множителя. Следовательно, исходное уравнение не разрешимо в целых числах x, y при y ≠ 0. Случай y = 0 также невозможен, поскольку тогда исходное уравнение принимает вид x 5 = 33, Так как Задача 6. Доказать, что уравнение (x — y) 3 + (y — z) 3 + (z — x) 3 = 30 не имеет решений в целых числах. Решение. Разложив левую часть на множители, приведем уравнение к виду (x — y)(y — z)(z — x) = 10. Заметим, что (x — y) + (y — z) + (z — x) = 0. С другой стороны, делителями 10 являются числа ±1, ±2, ±5, ±10. Нетрудно проверить, что сумма любых трех чисел из этого множества, дающих в произведении 10, не будет равнятьса 0. Задача 7. Решить в целых числах уравнение y 3 — x 3 = 91. Решение. Перепишем исходное уравнение в виде (y — x)(y 2 + xy + x 2 ) = 91. Делителями числа 91 являются ±1, ±91. Так как y 2 + yx + x 2 ≥ y 2 — 2|y||x| + x 2 = (|y| — |x|) 2 ≥ 0, то исходное уравнение равносильно совокупности
Таким образом, целочисленными решениями исходного уравнения являются пары (-6,-5) и (5,6). Задача 8. Решить в натуральных числах уравнение y 2 — x(x + 1)(x + 2)(x + 3) = 1. Решение. Заметим, что
Следовательно, исходное уравнение равносильно уравнению y 2 = (x 2 + 3x + 1) 2 или y = x 2 + 3x + 1. Таким образом, множество всех решений имеет вид <(x , x 2 + 3x + 1) | x Î N>. 2. Использование четности Задача 9. Решить в простых числах уравнение
Решение. Рассмотрим два случая в зависимости от четности переменной x. a) Пусть x — нечетное число. Подстановка x = 2t + 1 приводит исходное уравнение к виду (2t + 1) 2 — 2y 2 = 1, или 2y 2 = 4t(t + 1). Следовательно, 2 | y 2 . Так как y — простое число, то y = 2. Отсюда b) Пусть x — четное число. Так как x — простое число, то x = 2. Следовательно, Следовательно, уравнение (11) имеет в классе простых чисел единственное решение (3;2). Задача 10. Решить в целых числах уравнение
Решение. Одно решение очевидно: x = y = z = 0. Покажем, что других решений в целых числах уравнение не имеет. Будем доказывать от противного. Пусть x, y, z — ненулевое решение исходного уравнения. Так как x 2 + y 2 + z 2 — четное число, то по крайней мере одно из чисел x, y, z — четное. Используя симметрию уравнения (12), предположим, что x = 2x1. — четное число. Тогда 4|y 2 + z 2 . Это может быть лишь в том случае, когда y и z — четные. Действительно, если одно из этих чисел четное, а другое нечетное, то число y 2 + z 2 — нечетное и 4 Повторением приведенных выше рассуждений доказывается, что 2|x1, 2|y1, 2|z1, следовательно, 2 2 |x, 2 2 |y, 2 2 |z. Рассуждая аналогично, получим, что для любого n Î N 2 n |x, 2 n |y, 2 n |z Противоречие. Следовательно, уравнение (12) имеет единственное решение (0,0,0). Задача 11. Доказать, что уравнение
в целых числах не имеет решений, не равных нулю одновременно. Решение. Предположим, что числа x, y, z, не равные одновременно нулю, являются решением исходного уравнения. Видно, что число x — четное. Подстановка x = 2x1 дает 4x1 3 + y 3 + 2z 3 — 6x1yz = 0. Отсюда следует, что число y — четное, y = 2y1. Учитывая это, получим 2x1 3 + 4y1 3 + z 3 — 6x1y1z = 0. Следовательно, z — также четное число. После подстановки z = 2z1 уравнение принимает вид x1 3 + 2y1 3 + 4z1 3 — 6x1y1z1 = 0. Рассуждая аналогично, доказывается, что для любого n Î N 2 n |x, 2 n |y, 2 n |z. Противоречие. 3. Доказательство неразрешимости уравнений с использованием сравнений Задача 12. Решить в целых числах уравнение
Решение. Пусть x, y — целые числа, удовлетворяющие уравнению (14 ). Тогда x 2 + 1 ≡ 0(mod 3). Рассмотрим случаи, соответствующие различным остаткам от деления x на 3. a) Пусть x ≡ 0(mod 3). Тогда x 2 + 1 ≡ 1(mod 3), значит x 2 + 1 b) Пусть x ≡ 1(mod 3). Тогда x 2 + 1 ≡ 2(mod 3), следовательно, x 2 + 1 c) Пусть x ≡ 2(mod 3). Тогда x 2 + 1 ≡ 5 ≡ 2 Задача 13. Решить в целых числах уравнение
Решение. Пусть (x, y, z) — целочисленное решение уравнения (15). Так как x — нечетное число, следовательно, x 2 = (2k + 1) 2 = 4k(k + 1) + 1 ≡ 1(mod 8). По модулю 4 исходное уравнение принимает вид 1 — 2y 2 ≡ 3(mod 4) или y 2 ≡ -1(mod 2). Следовательно, y — нечетное число, отсюда y 2 ≡ 1(mod 8). Поэтому, по модулю 8 исходное уравнение будет иметь вид 1 — 2 ≡ 3(mod 8) Û 4 ≡ 0(mod 8). Полученное противоречие доказывает неразрешимость исходное уравнение в целых числах. Задача 14. Доказать, что уравнение x 3 + x + 10y = 20004 неразрешимо в целых числах. Решение. По модулю 5 исходное уравнение принимает вид
Рассмотрев все возможные остатки от деления x на 5, убеждаемся, что сравнение (16) неразрешимо. Следовательно, исходное уравнение также неразрешимо в целых числах. 4. Другие методы решения диафантовых уравнений Задача 15. Доказать, что уравнение x 3 + y 3 + z 3 = 2 имеет бесконечно много решений в целых числах. Решение. Положим x = a + b, y = a — b. Тогда x 3 + y 3 = 2a 3 + 6ab 2 . С учетом последнего равенства исходное уравнение принимает вид 2a 3 + 6ab 2 + z 3 = 2. Положив a = 1, получим z 3 = -6b 2 . Положим теперь b = 6t 3 . Отсюда z = -6t 2 , x = 1 + 6t 3 , y = 1 — 6t 3 . Таким образом, получено бесконечное множество решений исходного уравнения, соответствующих целочисленным значениям параметра t Задача 16. Доказать, что уравнение
имеет бесконечно много решений в натуральных числах. Решение. Нетрудно заметить, что (3,2) — одно из решений исходного уравнения. С другой стороны из тождества (x 2 + 2y 2 ) 2 — 2(2xy) 2 = (x 2 — 2y 2 ) 2 следует, что если (x, y) — решение уравнения (17), то пара (x 2 + 2y 2 , 2xy) также является его решением. Используя этот факт, рекуррентно определим бесконечную последовательность (xn , yn) различных решений исходного уравнения: (x1 , y1) = (3,2) и xn+1 = xn 2 + 2yn 2 , yn+1 = 2xnyn, n Î N * . Задача 17. Решить в целых числах уравнение Решение. Заметим, что слагаемые в левой части уравнения имеют одинаковый знак, а поскольку их сумма положительна, то каждое слагаемое также положительно. Применяя неравенство Коши, получим Следовательно, xyz = 1. Отсюда получим, что решениями могут быть только тройки (1,1,1), (1,-1,-1), (-1,-1,1), (-1,1,-1). Проверкой убеждаемся, что каждая из них действительно является решением исходного уравнения. Задача 18. Доказать, что уравнение x(x + 1) = 4y(y + 1) неразрешимо в целых положительных числах. Решение. Нетрудно заметить, что исходное уравнение равносильно уравнению x 2 + x + 1 = (2y + 1) 2 . Следовательно, x 2 2 2 или x 2x 3 + xy — 7 = 0. Решение. Из условия следует, что x должен быть делителем числа 7. Т. е. возможные значения x находятся среди чисел . Перебрав эти возможности, получаем решение уравнения: (1,5), (-1,-9), (7,-97), (-7,-99). Задача 20. Доказать, что уравнение x 2 + 1 = py, где p — простое число вида 4k+3, неразрешимо в целых числах. Решение. Предположим, что исходное уравнение разрешимо в целых числах. Тогда x 2 + 1 ≡ 0(mod p). Но, согласно малой теореме Ферма, -1 ≡ (-1) 2k+1 ≡ (x 2 ) 2k+1 ≡ x p-1 ≡ 1(mod p). Полученное противоречие доказывает неразрешимость исходного уравнения в Z. Задача 21. Доказать, что уравнение x 2 — y 3 = 7 неразрешимо в целых положительных числах. Решение. Если y — четное число, то x 2 ≡ 3(mod 4), что невозможно. Поэтому предположим, что y — нечетное число: y = 2k + 1. Тогда x 2 + 1 = y 3 + 8 = (y + 2)((y + 1) 2 + 3) = (y + 2)(4(k + 1) 2 + 3), Итак, число x 2 + 1 имеет делитель вида 4n + 3. Следовательно, оно имеет и простой делитель вида 4n + 3 (действительно, если бы все простые делители числа 4(k + 1) 2 + 3 имели вид 4n + 1, то и само число, являясь их произведением, имело бы вид 4n + 1. Однако последнее невозможно в силу предыдущей задачи. Задача 22. Доказать, что уравнение Решение. Положим d = (x , y), x1 = x /d, y1 = y /d. Так как x 2 + xy + y 2 = x 2 y 2 , следовательно,
Отсюда получаем, что x1|y1, y1|x1. Учитывая, что (x1,y1) = 1, делаем вывод, что x1 = y1 = 1. Таким образом, уравнение (18) принимает вид d 2 = 3, Отсюда следует требуемое утверждение. Задача 23. Решить в целых числах уравнение x + y = x 2 — xy + y 2 . Решение. Положим t = x + y. Так как Учитывая соотношение x + y = (x + y) 2 — 3xy, рассмотрим случаи, соответствующие целочисленным значениям t из отрезка [0;4]. a) t = 0
b) t = 1
c) t = 2
d) t = 3
e) t = 4
Таким образом, целочисленными решениями исходного уравнения являются пары (0,0), (0,1), (1,0), (1,2), (2,1), (2,2). Задачи для самостоятельного решения
Видео:Решение уравнения третьей степени x³-9x-12=0Скачать  Вторая глава: Диофантовы уравнения степени выше первой. Решение диофантовых уравнений методом разложения на множители
Диофантовы уравнения степени выше первой. Решение диофантовых уравнений методом разложения на множители. Задача 1. Решить в целых числах уравнение Решение. Запишем уравнение в виде Произведение двух целых чисел может равняться 1 только в том случае, когда оба они равны 1. Т. е. исходное уравнение равносильно совокупности
с решениями (0,0) и (2,2). Задача 2. Решить в простых числах уравнение Решение. Рассмотрим два случая в зависимости от четности переменной x. a) Пусть x — нечетное число. Подстановка x = 2t + 1 приводит исходное уравнение к виду Следовательно, y2 кратно 2. Так как y — простое число, то y = 2. Отсюда х= b) Пусть x — четное число. Так как x — простое число, то x = 2. Следовательно, Следовательно, уравнение имеет в классе простых чисел единственное решение (3;2). Задача 3. Доказать, что уравнение имеет бесконечно много решений в натуральных числах. Решение. Нетрудно заметить, что (3,2) — одно из решений исходного уравнения. С другой стороны из тождества (x2 + 2y2)2 — 2(2xy)2 = (x2 — 2y2)2 следует, что если (x, y) — решение данного уравнения, то пара (x2 + 2y2 , 2xy) также является его решением. Используя этот факт, рекуррентно определим бесконечную последовательность (xn, yn) различных решений исходного уравнения: (x1 , y1) = (3,2) и xn+1 = xn2 + 2yn2, yn+1 = 2xnyn, n ∈ N*. Задача 4. Доказать, что уравнение неразрешимо в целых положительных числах. Решение. Нетрудно заметить, что исходное уравнение равносильно уравнению Видео:Классический способ решения Диофантовых уравнений ➜ Решите уравнение в целых числах ➜ 13x-7y=6Скачать  Линейное диофантово уравнение и 4 способа его решенияРазделы: Математика Првило 1. Если с не делится на d, то уравнение ах + ву = с не имеет решений в целых числах. Н.О.Д.(а,в) = d. Правило 2. Чтобы найти решение уравнения ах + ву = с при взаимно-простых а и в, нужно сначала найти решение (Хо ; уо) уравнения ах + ву = 1; числа СХо , Суо составляют решение уравнения ах + ву = с. Решить в целых числах (х,у) уравнение Первый способ. Нахождение частного решения методом подбора и запись общего решения. Знаем, что если Н.О.Д.(а;в) =1, т.е. а и в взаимно-простые числа, то уравнение (1) имеет решение в целых числах х и у. Н.О.Д.(5;8) =1. Методом подбора находим частное решение: Хо = 7; уо =2. Итак, пара чисел (7;2) — частное решение уравнения (1). Значит, выполняется равенство: 5 x 7 – 8 x 2 = 19 … (2) Вопрос: Как имея одно решение записать все остальные решения? Вычтем из уравнения (1) равенство (2) и получим: 5(х -7) – 8(у — 2) =0. Отсюда х – 7 = Тем самым все целые решения исходного уравнения можно записать в таком виде: Второй способ. Решение уравнения относительно одного неизвестного. Решаем это уравнение относительно того из неизвестных, при котором наименьший (по модулю) коэффициент. 5х — 8у = 19 Остатки при делении на 5: 0,1,2,3,4. Подставим вместо у эти числа. Если у = 0, то х = Если у =1, то х = Если у = 2, то х = Если у =3, то х = Если у = 4 то х = Итак, частным решением является пара (7;2). Тогда общее решение: Третий способ. Универсальный способ поиска частного решения. Для решения применим алгоритм Евклида. Мы знаем, что для любых двух натуральных чисел а, в, таких, что Н.О.Д.(а,в) = 1 существуют целые числа х,у такие, что ах + ву = 1. 1. Сначала решим уравнение 5m – 8n = 1 используя алгоритм Евклида. 2. Затем найдем частное решение уравнения (1)по правилу 2. 3. Запишем общее решение данного уравнения (1). 1. Найдем представление: 1 = 5m – 8n. Для этого используем алгоритм Евклида. 8 = 5 5 = 3 3 = 2 Из этого равенства выразим 1. 1 = 3 — 2 = 3 — 5 = 5 2. Частное решение уравнения (1): Хо = 19m; уо =19n. Отсюда получим: Хо =19 Пара (-57; -38)- частное решение (1). 3. Общее решение уравнения (1): Четвертый способ. Геометрический. 1. Решим уравнение 5х – 8у = 1 геометрически. 2. Запишем частное решение уравнения (1). 3. Запишем общее решение данного уравнения (1).
Отложим на окружности последовательно друг за другом равные дуги, составляющие На 5 – ом шаге получили вершину, соседнюю с начальной, при этом сделали 3 полных оборота и еще прошли Итак, Хо = 5, уо =3 является частным решением уравнения 5х – 8у = 1. 2. Частное решение уравнения (1): Хо = 19 3. Общее решение уравнения (1): 🌟 ВидеоКак решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать  Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать  ПЕРЕЧНЕВЫЕ ОЛИМПИАДЫ. Диофантовы уравненияСкачать  Формула Кардано. Решение уравнений третьей степени.Скачать  КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать  РЕШАЕМ ДИОФАНТОВОЕ УРАВНЕНИЕ | ПРОСТЫМИ СЛОВАМИСкачать  Решение уравнений третьей степени (формула Кардано)Скачать  Решите уравнение в целых числах 5x-4y=3 ➜ Как решать Диофантовы уравнения?Скачать  Решение диофантовых уравненийСкачать  Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать  Диофантовы уравнения x²+xy-y=2Скачать  Диофантовы уравнения x³-y³=91Скачать  ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать  Как решать кубические уравнения Решите уравнение 3 степени 9 класс Разложить на множители ДелениеСкачать  Решите уравнение в целых числах 3x^2+5y^2=345 ✱ Диофантовы уравнения ✱ Как решать?Скачать  Математика | Кубические уравнения по методу СталлонеСкачать  Можно ли решить уравнение 5-й степени? – математик Алексей Савватеев | НаучпопСкачать  Уравнение четвертой степениСкачать  |
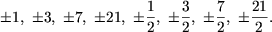
(i = 1. n), которые не равны нулю, равны между собой по абсолютной величине. Из соотношения 
следует, что числа 
. Тогда уравнение (10) имеет следующее решение: 
где t2, t3, . tn — произвольные целые числа. Отсюда, учитывая проведенные замены, получается и решение уравнения (7). Отметим, что при получении решения уравнения (10) использовался лишь факт, что 
исходное уравнение не имеет целочисленных решений и в случае y = 0.
т. е. уравнение неразрешимо в простых числах.
y 2 + z 2 . Если же оба эти числа (z и y) нечетные, то y 2 + z 2 = (2u + 1) 2 + (2v + 1) 2 = 4(u 2 + v 2 + u + v) + 2 ≡ 2(mod 4),
не имеет решений в целых положительных числах.
то должно выполнятся неравинство 
откуда t Î [0;4].
Указание. Применить неравинство Коши. 
где параметр p — простое число больше 2. 
=3.
т. е. уравнение неразрешимо в простых числах.
. Из полученного равенства видно, что число (х – 7) будет целым тогда и только тогда, когда (у – 2) делится на 5, т.е. у – 2 = 5n, где n какое-нибудь целое число. Итак, у = 2 + 5n, х = 7 + 8n, где n 
Z.
n 
х = 
.
=
.
=
.
= 
= 7 
=
.
=
.
1 + 3.
.
= 3 – (5 — 3 
=
= 3 
= (8 — 5 
— 5 
8
2 -5
(-2). Итак, m = -3, n = -2.
; уо =19 
.
n 
-ю часть полной окружности. За 8 шагов получим все вершины правильного вписанного в окружность 8-угольника. При этом сделаем 5 полных оборотов.
— ю часть окружности, так что х 
уо =19 
n