Решение дифференциальных уравнений заданных неявно

Видео:18+ Математика без Ху!ни. Производная неявной функции.Скачать

1. Неявные методы

Методы численного решения ОДУ, с которыми мы познакомились в первом разделе этого курса (метод Эйлера, метод средней точки и т. п.), называются «явными» методами. Однако иногда система ОДУ может стать «жесткой», а решать такие системы явными методами неудобно. В этом случае желательно изменить формулировку задачи так, что не пришлось иметь дело с жесткой системой. Но это не всегда возможно, поэтому вы должны уметь решать жесткие ОДУ. Для этого, как правило, используют методы решения, которые называются «неявными».

Видео:27. Дифференцирование неявной функции двух переменныхСкачать

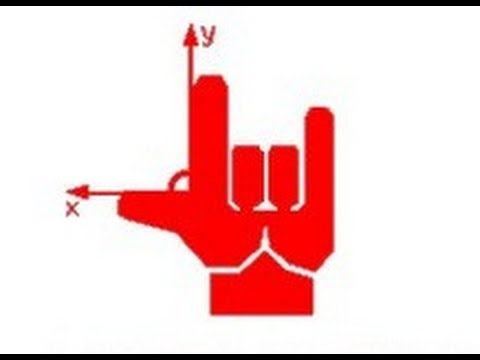
2. Пример жесткого ОДУ

Во-первых, в чем смысл и причина появления жестких уравнений? Давайте рассмотрим пример, который часто возникает в динамике. Предположим, что у нас есть частица, с координатами ((x(t),y(t))) , и предположим, что мы хотим, чтобы ее (y) -координата всегда оставалась равной нулю. Один из способов добиться этого — добавить слагаемое (-ky(t)) , к производной (dot(t)) , где (k) — большая положительная постоянная. Если (k) достаточно велико, то частица никогда не уйдет далеко от (y(t)=0) , так как слагаемое (-ky(t)) всегда приведет (y(t)) обратно к нулю. Предположим далее, что мы хотим, чтобы пользователь мог перемещать частицу как угодно вдоль оси (x) . Дифференциальное уравнение, описывающее движение данной системы, будет иметь вид

(Кроме того, мы предполагаем, что частица не запускается из (y_0=0) ). В результате частица будет сильно притягиваться к прямой (y = 0) , и менее сильно — к (x = 0) . Если решать ОДУ на достаточно продолжительном интервале времени, то частица рано или поздно попадет в точку ((0, 0)) и останется в ней.

Теперь предположим, что для решения уравнения мы используем метод Эйлера. Если сделать шаг размера (h) , то получим

Если мы посмотрим на (у) -компоненту этого уравнения, то увидим, что при (|1-hk|>1) , вычисленное нами (y_) будет по модулю больше, чем (|у_0|) . Другими словами, при (|1-hk|>1) метод Эйлера будет неустойчив: каждый шаг приводит к увеличению (y_) по сравнению с предыдущим значением и приближенное решение будут все дальше отклоняться от нуля. Таким образом, для обеспечения устойчивости метода нужно, чтобы (1-hk>-1) или (hk . Самый большой шаг, который мы можем сделать не нарушив устойчивости, должен быть меньше (2/k) .

Теперь, если (k) – большое число, мы вынуждены делать очень маленькие шаги. Это означает, что частица будет двигаться к ((0,0)) мучительно медленно. Даже если взять (y_0) очень близким к нулю, то придется делать настолько маленькие шаги, что изменение (x) -координаты будет практически незаметно. Вот так выглядит жесткое ОДУ. В данном случае жесткость возникает из-за слишком большого (k) , призванного удержать частицу возле прямой (у = 0) . Позже, когда мы будем рассматривать частицы, соединенные пружинами, мы увидим то же самое явление: от жесткости пружины и происходит термин «жесткое» ОДУ. Даже если мы используем более совершенный численный метод, такой как метод Рунге-Кутта 4-го порядка, это лишь слегка улучшит ситуацию с выбором величины шага, но мы все равно будем иметь серьезные вычислительные проблемы.

Теперь, как мы уже говорили выше, нужно попытаться переформулировать свою задачу так, чтобы избежать появления жесткого ОДУ. Если же это не получится, то нужно использовать неявный метод решения ОДУ. Метод, который мы покажем ниже, является самым простым из неявных методов. Он основан на том, что шаг обычного метода Эйлера выполняется «наоборот».

Видео:11. Производная неявной функции примерыСкачать

3. Решение жесткого ОДУ

Пусть дано дифференциальное уравнение

Формула явного метода Эйлера

продвигает систему вперед на шаг (h) во времени. Для жестких систем, однако, удобнее заменить эту формулу на следующую

То есть, нам нужно вычислить (f) в точке, в которую мы стремимся попасть ( (textbf_) ), а не в исходной ( (textbf_0) ). (Если представить, что время может двигаться в обратном направление, то смысл этого уравнения очевиден. Оно говорит: «если вы находитесь в (textbf_) , и сделаете шаг (-hf (textbf_)) , то попадете в (textbf_0) ». Так что если ваше ДУ представляет собой систему, движущуюся вспять во времени, то этот шаг имеет смысл. Это просто поиск точки (textbf_) такой, что если запустить время вспять, вы в конечном итоге окажетесь в (textbf_0) .) Таким образом, мы ищем точку (textbf_) такую, что (f) , вычисленная в ней и умноженная на (h) , приводит к исходной точке (textbf_0) . К сожалению, найти (textbf_) из уравнения eqref в общем случае невозможно, если только (f) не является линейной функцией.

Чтобы справиться с этим, заменим (f (textbf_)) линейной аппроксимацией, основанной на разложении (f) в ряд Тейлора. Введем обозначение (Deltatextbf=textbf_-textbf_0) . Подставив его в уравнение eqref, получим

Теперь заменим (f(textbf_0 + Deltatextbf)) следующим приближением

(Заметим, что поскольку (f(textbf_0)) является вектором, то производная (f^prime(textbf_0)) является матрицей.) Используя это приближение, мы можем записать (Deltatextbf) как

Разделим обе части последнего соотношения на (h) и перепишем результат в виде

где (I) — единичная матрица.

Разрешая это соотношение относительно (Deltatextbf) , получим

Вычисление (textbf_=textbf_0+Deltatextbf) для неявного метода очевидно требует больших вычислительных затрат, чем при использовании явного метода, так как мы должны решать систему линейных уравнений на каждом шаге. Хотя это может показаться серьезным недостатком (в вычислительном плане), не отчаивайтесь (пока). Для многих классов задач, матрица (f^prime) будет разреженной — например, для «решетки» частиц, соединенных пружинами, (f^prime) будет иметь структуру, которая соответствует связям между частицами. (Обсуждение разреженности и методов решений, применимых в этом случае, см. Baraff и Witkin [1]. Основной материал в Press et al. [2] также будет полезен.) В результате, как правило, можно решить уравнение eqref в линейном времени (т. е. за время, пропорциональное размерности (textbf) ). Выигрыш в таких случаях будет весьма существенным: мы, как правило, можем делать большие шаги по времени без потери устойчивости (т. е. без расхождения, как это происходит для явного метода, если длина шага слишком велика). Время, необходимое для решения каждой линейной системы, таким образом, более чем компенсируется тем, шагов можно зачастую сделать на порядки больше, чем при использовании явных методов. (Конечно, код, необходимый для реализации всего этого, гораздо сложнее, чем в явном случае; как мы уже говорили: переделывайте свои задачи в нежесткие, а если не получается, то платите положенную цену.)

Применим теперь неявный метод для решения уравнения eqref. В нашем случае (f(textbf(t))) равно

Дифференцирование по (textbf) дает

Тогда матрица ((1/h)textbf — f^(textbf_0)) будет равна

Обращая эту матрицу и умножая на (f(textbf_0)) , получим

Какова же предельная длина шага в этом случае? Ответ: нет предела! Если позволить (h) расти до бесконечности, мы получаем следующее

Это означает, что мы достигнем (textbf_=textbf_0 + (-textbf_0)=0) за один шаг! В общем случае для жесткого ОДУ мы не сможем сделать шаг произвольного размера, но мы сможем сделать его гораздо большим, чем если бы использовали явный метод. Дополнительные расходы на решение системы линейных уравнений компенсируются экономией, возникающий благодаря возможности сделать меньше шагов.

Видео:Производная неявной функцииСкачать

4. Решение уравнений второго порядка

Большинство задач динамики записывается в виде ДУ 2-го порядка

Это уравнение легко преобразуется систему ДУ 1-го порядка, добавлением новых переменных. Если мы определим (textbf=dot<textbf>) , то сможем переписать уравнение eqref в виде

что представляет собой систему ДУ 1-го порядка. Однако, применяя обратный (неявный) метод Эйлера к уравнению eqref, получим линейную систему размера (2n times 2n) где (n) — размерность (textbf) . Простое преобразование позволяет уменьшить размер линейной системы до (n times n) . Важно отметить, что обе системы — исходная и преобразованная — будут иметь одинаковую степень разреженности. Таким образом, решение системы меньшего размера будет выполняться быстрее.

Система (n times n) , которая должна быть решена, получается следующим образом. Введем для краткости следующие обозначения (textbf_0=textbf(t_0)) и (textbf_0=textbf(t_0)) . Определяем (Deltatextbf) и (Deltatextbf) как (Deltatextbf = textbf(t_0+h)-textbf(t_0)) и (Deltatextbf = textbf(t_0+h)-textbf(t_0)) . Очередное приближение по неявному методу Эйлера, примененному к уравнению eqref, дает в результате

Применяя к (f) разложение в ряд Тейлора, которое в данном контексте является функцией и (textbf) и (textbf) , получим приближение 1-го порядка

В этом уравнении, производная (partial f / partialtextbf) оценивается в точке ((textbf_0, textbf_0)) и аналогично вычисляется (partial f / partialtextbf) . Подставляя это приближение в уравнение eqref, получим линейную систему

Подставив во вторую строку последнего равенства соотношение (Deltatextbf = h(textbf_0 + Deltatextbf)) (т. е. первую строку того же равенства), придем к

Вводя единичную матрицу (I) и перегруппировав члены, получим соотношение

из которого находим (Deltatextbf) . А зная (Deltatextbf) легко вычислить (Deltatextbf = h(textbf_0 + Deltatextbf)) .

Выше, мы предполагали, что функция (f) не зависит явно от времени. Если же (f) зависит от времени явно (например, если (f) описывает изменяющиеся во времени внешние силы), то в уравнение eqref добавляется член, позволяющий учесть эту зависимость

Видео:11.1. Касательная к неявной функции / производная неявной функции ПРИМЕРЫСкачать

Ссылки

1. D. Baraff and A. Witkin. Large steps in cloth simulation. Computer Graphics (Proc. SIGGRAPH), 1998.
2. W.H. Press, B.P. Flannery, S.A. Teukolsky, and W.T. Vetterling. Numerical Recipes. Cambridge University Press, 1986.

Читайте также

Видео:Первая и вторая производная неявной функцииСкачать

Комментарии

Дмитрий Храмов
Компьютерное моделирование и все, что с ним связано: сбор данных, их анализ, разработка математических моделей, софт для моделирования, визуализации и оформления публикаций. Ну и за жизнь немного.

Видео:Математика Без Ху!ни. Производная функции, заданной параметрически.Скачать

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Видео:14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Примеры решения дифференциальных уравнений с ответами

Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Видео:Неявные дифференциальные уравнения первого порядкаСкачать

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь

переписываем дифференциальное уравнение, получаем

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем

Далее интегрируем полученное уравнение:

В данном случае интегралы берём из таблицы:

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

Задание

Найти частное решение дифференциального уравнения

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

Если – это константа, то

0]» title=»Rendered by QuickLaTeX.com» />

– тоже некоторая константа, заменим её буквой С:

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

Ответ

Задание

Решить дифференциальное уравнение

Решение

В первую очередь необходимо переписать производную в необходимом виде:

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

После разделения переменных, интегрируем уравнение, как в примерах выше.

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

Приводим полученный общий интеграл к виду: F(x,y)=C:

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

Получаем общее решение:

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Задание

Решить дифференциальное уравнение

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

В данном случае константу C считается не обязательным определять под логарифм.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

можно выразить функцию в явном виде.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Проверка

Необходимо проверить, выполняется ли начальное условие:

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

дифференциальному уравнению. Для этого находим производную:

Подставим полученное частное решение

и найденную производную в исходное уравнение

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Ответ

Задание

Найти частное решение ДУ.

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

Подставляем в общее решение

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Левую часть интегрируем по частям:

В интеграле правой части проведем замену:

(здесь дробь раскладывается методом неопределенных коэффициентов)

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

🔍 Видео

[Calculus | глава 6] Неявное дифференцирование — что здесь происходит?Скачать

Частное решение дифференциального уравнения. 11 класс.Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Как находить производную неявной функции - bezbotvyСкачать

Математический анализ, 31 урок, Дифференцирование сложных и неявных функцийСкачать

Производная функции заданной неявноСкачать

Математика без Ху!ни. Логарифмическое дифференцирование.Скачать

ВМ. 2.5 Дифференцирование функций, заданных параметрическиСкачать