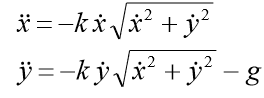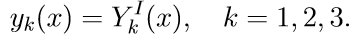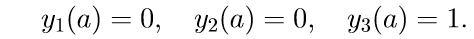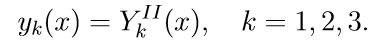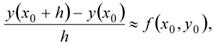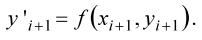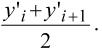Метод позволяет решать системы обыкновенных дифференциальных уравнений (ОДУ) первого порядка следующего вида:
которые имеют решение:
где t — независимая переменная (например, время); X, Y и т.д. — искомые функции (зависимые от t переменные). Функции f, g и т.д. — заданы. Также предполагаются заданными и начальные условия, т.е. значения искомых функций в начальный момент.
Одно диф. уравнение — частный случай системы с одним элементом. Поэтому, далее речь пойдет для определенности о системе уравнений.
Метод может быть полезен и для решения диф. уравнений высшего (второго и т.д.) порядка, т.к. они могут быть представлены системой диф. уравнений первого порядка.
Метод Рунге-Кутта заключается в рекурентном применении следующих формул:
Реализация Метода Рунге-Кутта на Delphi может выглядеть так (привожу полностью модуль):
Модуль полностью работоспособен. Возвращаемое функцией Runge_Kutt значение — код ошибки. Вы можете дополнить список ошибок по своему усмотрению. Рассчитанные функции системы помещаются в массив Res. Чтобы не загромождать код, в модуле опущены проверки (типа блоков try). Рекомендую их добавить по своему усмотрению.
Ниже приводится описание функции Runge_Kutt и типов, использующихся в модуле.
- FunArray — вектор функций (правых частей уравнений системы);
- First, Last — начальная и конечная точки расчетного интервала;
- Steps — число шагов по расчетному интервалу;
- InitArray — вектор начальных значений
- var Res — матрица результатов включая независимую переменную.
В модуле описаны типы:
Функция возвращает коды ошибок:
- 0 — нет ошибок;
- 100 — число уравнений не равно числу начальных условий.
Решение содержится в переменной-матрице Res. Первый индекс матрицы относится к переменной (0 — независимая переменная, 1 — первая зависимая и т.д.), второй — к номеру расчетной точки (0 — начальная точка).
Рассмотрим один пример использования модуля. Создадим новое приложение и подключим к нему модуль. На форме приложения разместим кнопку Button1 и область текста Memo1. Поместим в приложение две функции и обработчик нажатия кнопки:
Нажатие кнопки приведет к расчету точек системы, которые будут выведены в текстовую область.
Модуль с примером и справкой можно скачать бесплатно по адресу RK.zip (ZIP, 15,3Kb) (русский вариант). Английский вариант (условно-бесплатный) можно скачать по адресу RK_Eng.zip (ZIP, 23.4Kb)
- Ссылки
- Оставить комментарий
- Комментарии
- Численное решение математических моделей объектов заданных системами дифференциальных уравнений
- Введение:
- Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
- Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
- Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
- Решение краевой задачи с поточно разделёнными краевыми условиями
- Вывод
- Численные методы решения обыкновенных дифференциальных уравнений. Метод Эйлера и методы Рунге-Кутта для решения дифференциальных уравнений
- 📽️ Видео
Видео:6.4 Явные методы Рунге-КуттыСкачать

Ссылки
- http://sadovoya.narod.ru/RK.zip (русский вариант).
- http://sintreseng.narod.ru/RK_Eng.zip (английский, условно-бесплатный вариант)
Видео:Методы численного анализа - Метод Рунге-Кутта для ОДУ 2 порядкаСкачать

Оставить комментарий
Видео:Решение ОДУ методом Рунге-Кутта 4 порядка (программа)Скачать

Комментарии
Скачала по Вашей ссылке русский вариант, изменила для своей системы диф. уравнений, но при запуске выдаёт ошибку :
Project Ex.exe raised exception class EOverflow with message ‘ Floating point overflow ‘
Помогите, пожалуйста .
Вот изменённый мною модуль:
unit Unit1;
interface
uses
SysUtils, Forms, StdCtrls, Controls, Classes, Dialogs, Math;
type
TForm1 = class(TForm)
Memo1: TMemo;
rk_But: TButton;
procedure rk_ButClick(Sender: TObject);
private
public
end;
var
Form1: TForm1;
pn,k,ro,Pzv: Extended;
implementation
uses rk_method, Windows;
procedure Syst (var t: TFloat; var X: TFloatVector;
var RP: TFloatVector);
const
fdr1=0.503;
fdr2=0.503;
fdr3=0.196;
W1=179.8928;
W2=3773.8568;
W3=2504.1203;
b1=55.9203;
b2=98.6;
b3=98.6;
Ls1=3.78;
Ls2=9;
Ls3=15.3;
Svidj2=1352.438;
Svidj3=1352.438;
my=0.62;
vk=30;
m=1.2;
L1=30.969;
L2=42.131;
delta1=0;
begin
pn:=2.5*Power(10,4);
k:=6*Power(10,-7);
ro:=8.5*Power(10,-7);
Pzv:=3.919*Power(10,7);
RP[0] := (1/(k*W1))*(my*fdr1*sqrt(2/ro)*sqrt(Abs(pn-X[0]))-my*fdr2*sqrt(2/ro)*sqrt(Abs(X[0]-X[1]))-(delta1*delta1*delta1*b1)/(12*ro*vk*Ls1)*X[0]); // dp1/dt
RP[1] := (1/(k*W2))*(my*fdr2*sqrt(2/ro)*sqrt(Abs(X[0]-X[1]))-my*fdr3*sqrt(2/ro)*sqrt(Abs(X[1]-X[2]))-(X[4]*X[4]*X[4]*b2)/(12*ro*vk*Ls2)*X[1]); // dp2/dt
RP[2] := (1/(k*W3))*(my*fdr3*sqrt(2/ro)*sqrt(Abs(X[1]-X[2]))-(X[6]*X[6]*X[6]*b3)/(12*ro*vk*Ls3)*X[2]); // dp3/dt;
RP[3] := (((Svidj2*X[1]*(L1+L2))/L1)-Pzv)*(2/m); // dv2/dt
RP[4] := X[3]; // d delta2/dt
RP[5] := (((Svidj3*X[2]*(L1+L2))/L2)-Pzv)*(2/m); // dv3/dt
RP[6] := X[5]; // d delta3/dt
end;
procedure TForm1.rk_ButClick(Sender: TObject);
var
I, t1, t2: Cardinal;
tOut, InitConds: TFloatVector;
XOuts: TFloatMatrix;
Points: Cardinal;
First, Last: TFloat;
StepsFact: Cardinal;
Count: Word;
begin
Memo1.Clear;
First := 0.0;
Last := 10.0;
Count:= 7;
Points:=10+1; //11 points for output
StepsFact:=1000000; //all steps inside function = 10*StepsFact
try
SetLength(InitConds, Count);
InitConds[0]:=0.0; //x0(0)=0
InitConds[1]:=0.0; //x1(0)=0
InitConds[2]:=0.0; //x2(0)=0
InitConds[3]:=0.0; //x3(0)=0
InitConds[4]:=0.0; //x4(0)=0
InitConds[5]:=0.0; //x5(0)=0
InitConds[6]:=0.0; //x6(0)=0
SetLength(tOut, Points);
SetLength(XOuts, Count, Points);
except
ShowMessage(‘Out of memory. ‘);
exit;
end;
Видео:6.1 Численные методы решения задачи Коши для ОДУСкачать
Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
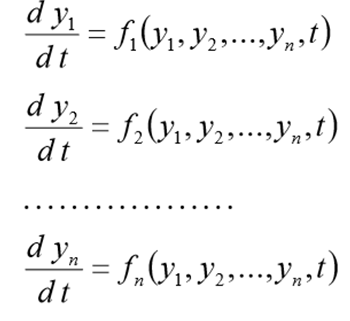
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши
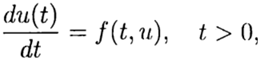

по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 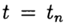

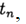


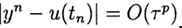

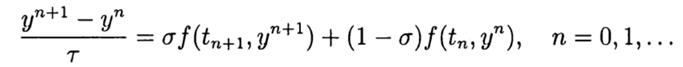
При 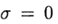
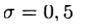
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
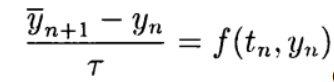
а на этапе корректора (уточнения) — схема
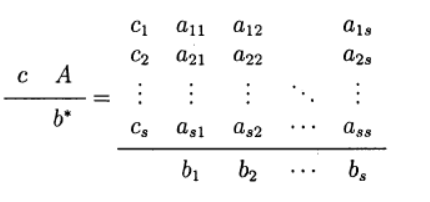
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
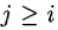

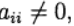

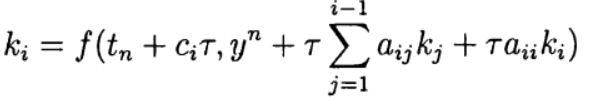
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 
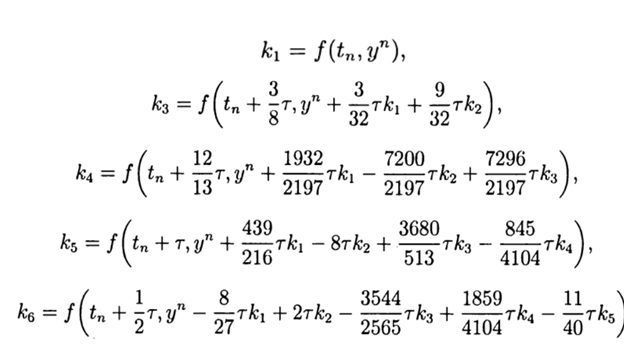
С учётом(9) общее решение имеет вид:
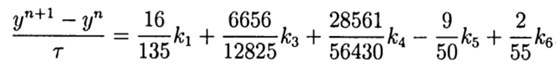
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
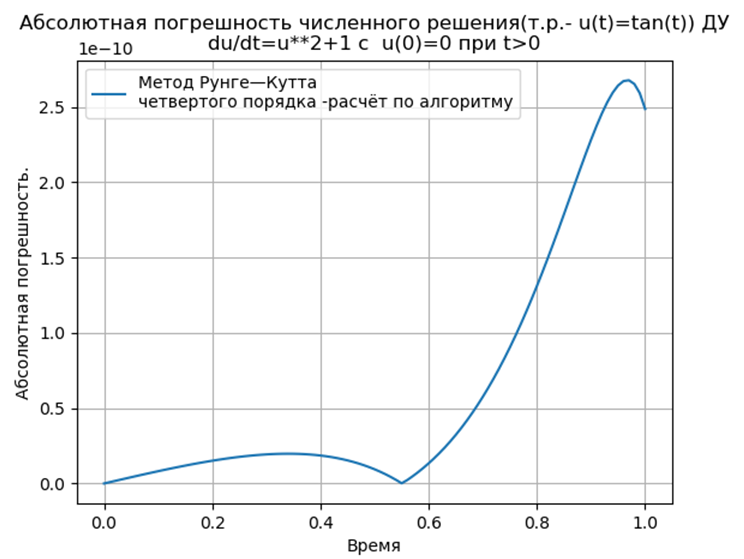
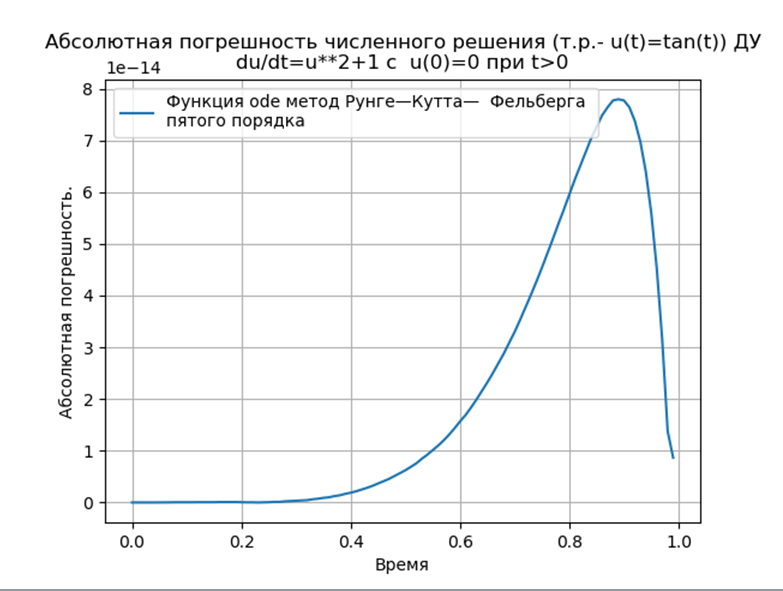
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
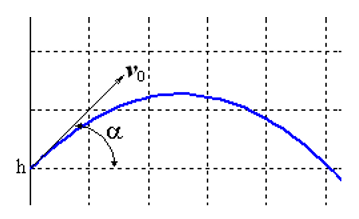
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 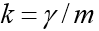
К системе следует добавить начальные условия: 

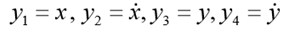
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
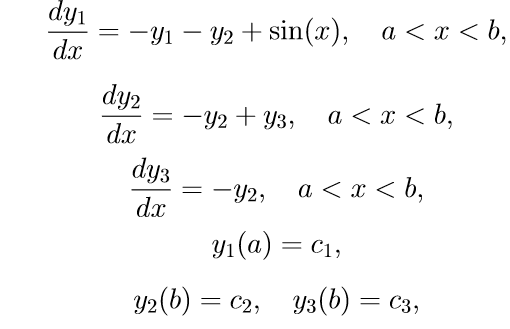
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 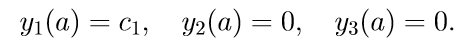
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 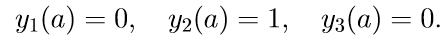
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 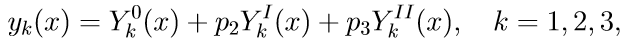
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
Видео:3_11. Алгоритм Рунге-КуттыСкачать

Численные методы решения обыкновенных дифференциальных уравнений. Метод Эйлера и методы Рунге-Кутта для решения дифференциальных уравнений
Суть метода Эйлера заключается в переходе от бесконечно малых приращений в уравнении к конечным: 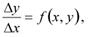
т.е. в замене производной приближенным конечно-разностным отношением:
где h = ∆х — шаг интегрирования.
Отсюда 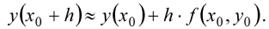
Рассматривая приближенное решение в точке 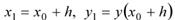
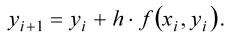
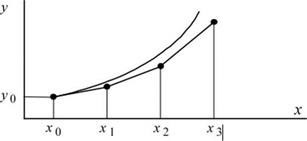
Метод Эйлера может быть интерпретирован геометрически следующим образом: функцию у(х) заменяют ломаной, представляющей собой отрезки касательных к этой функции в узлах (рис. 5.1).
Рис. 5.1. Метод Эйлера
Достоинствами метода Эйлера являются его простота и наглядность, недостатками — относительно невысокая точность (он имеет первый порядок точности) и систематическое накопление ошибки. Точность и устойчивость решения в значительной степени зависят от величины шага интегрирования. Для оценки погрешности и выбора шага может быть применена формула Рунге 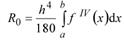
Методы Рунге-Кутта второго порядка
Методы Рунге-Кутта второго порядка основаны на разложении функции у(х) в ряд Тейлора и учете трех его первых членов (до второй производной включительно).
Метод Рунге-Кутта второго порядка с полным шагом реализуется по формуле:
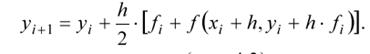
Его геометрическая интерпретация (рис. 6.1.) заключается в следующем:
1. Приближенно вычисляют значение функции в точке xi+h по формуле Эйлера 
2. Находят средний наклон на шаге h:
3. По этому наклону уточняют значение yi+1 по формуле (6.1.).
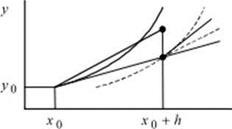 Рис. 6.1. Метод Рунге-Кутта второго порядка с полным шагом Рис. 6.1. Метод Рунге-Кутта второго порядка с полным шагом |
Формула метода Рунге-Кутта второго порядка с половинным шагомимеет вид
Рисунок 6.3. Метод Рунге-Кутта второго порядка с половинным шагом
Метод Рунге-Кутта четвертого порядка
📽️ Видео
Метод Рунге Кутты 2 и 4 порядковСкачать

Решение ОДУ: метод Рунге КуттаСкачать

04 Метод Рунге-Кутты 4-го порядкаСкачать

4a. Методы Рунге-КуттаСкачать

Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Метод ЭйлераСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Явный метод Рунге-Кутты второго порядка для решения задачи Коши. Контрольная работа МФТИСкачать

06 Неявные методы Рунге-КутыСкачать

Видеоурок "Системы дифференциальных уравнений"Скачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать








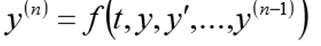
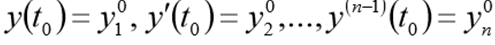


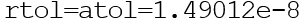
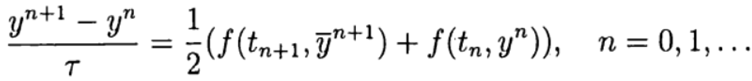
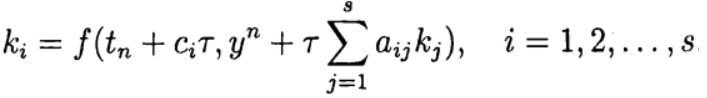
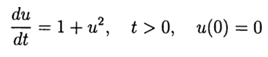 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга