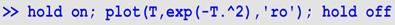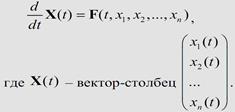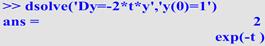Решение дифференциальных уравнений в частных производных matlab

Видео:Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Применение MATLAB для решения уравнений в частных производных

Для своего варианта функционала выведите дифференциальное уравнение Эйлера-Остроградского и решите его c помощью PDE Toolbox MATLAB.

Видео:Практическая работа 2. Работа в MATLABСкачать

Примечание: Если на рисунке указано “r = ” – то это часть окружности, если символа “r ” нет – то часть эллипса.

Начало координат − в левом нижнем углу. Граничные условия: на верхней дуге u = 10−3(y−0.15), на остальных сторонах u = 0.

Приложить файл для программы PDE Toolbox MATLAB.
Ниже указан пример готового решения задачи

Видео:MatLab. Решение дифференциального уравнения.Скачать

Применение MATLAB для решения уравнений в частных производных

Рассмотрим графические возможности МАТЛАБ на примере вывода решения дифференциального уравнения в частных производных Эйлера-Остроградского.

Пример 1. Найти экстремаль функционала:

в прямоугольной области xÎ[0,a]; yÎ [0,b], показанной на рис.3.

Рис.3. Область решения примера 1

Граничные условия: на правой стороне x = a:

на остальных сторонах z = 0.

Выведем вначале уравнение Эйлера-Остроградского вида:

,

или, после сокращения на 2:

. (8)

Граничные условия по переменной y однородные, поэтому будем искать решение в виде ряда Фурье по собственным функциям Yn(y), которые равны:

.

Ищем решение в виде ряда:

. (9)

Это решение удовлетворяет граничным условиям на нижней и верхней сторонах: при y=0 и y=b.

Для нахождения функций Xn(x) подставим решение (9) в уравнение (8):

.

Левая часть данного уравнения является разложением в ряд Фурье по Yn(y). Разложим в такой же ряд правую часть этого уравнения. Собственно, она уже разложена: в этом ряду присутствует только первый член (n=1), а коэффициенты при остальных гармониках равны нулю. Известно, что два ряда Фурье тождественны друг другу тогда и только тогда, когда равны все их коэффициенты. Поэтому из полученного уравнения можно получить бесконечную систему дифференциальных уравнений для функций Xn(x):

(10)

Граничные условия для данного уравнения можно получить, раскладывая граничные условия на левой и правой сторонах в ряд Фурье по Yn(y). На левой стороне x=0 имеем z=0, и, следовательно, коэффициенты разложения данной функции нулевые:

. (11)

На правой стороне x=a имеем граничное условие:

Подставим в него решение (9):

Это возможно тогда и только тогда, когда:

(12)

Решаем систему дифференциальных уравнений (10) при граничных условиях (11) и (12). При n>1 имеем:

;

. (13)

Подставляем граничные условия:

Во втором уравнении второй множитель (гиперболический синус) не равен нулю, поэтому C2=0. Следовательно, .

Далее найдем X1(x). Дифференциальное уравнение для него – это 1-е уравнение системы (10). Для решения такого уравнения следует взять сумму общего решения соответствующего однородного уравнения вида (13) и частного решения неоднородного уравнения. В результате получим:

Значения произвольных постоянных С1 и С2 найдем из граничных условий (11) и (12):

.

Решением рассматриваемой задачи является первая гармоника ряда:

График (рис.4) этой функции при a = 1 и b = 2 выглядит следующим образом:

clear all % очистили память

a=1; % задали размеры

[X, Y]=meshgrid(x, y); % сетка

b^2*X/pi^2).*sin(pi*Y/b); % вычисляем функцию

surf(X, Y,U) % рисуем поверхность

‘FontName’,’Times New Roman Cyr’,’FontSize’,12)

da=daspect; % текущие масштабы осей

da(1:2)=min(da(1:2)); % одинаковые масштабы

daspect(da); % установили одинаковые масштабы

title(‘bf Пример 1’)

xlabel(‘itx’) % ось OX

ylabel(‘ity’) % ось OY

zlabel(‘iturm(itxrm,ityrm)’) % ось OZ

Видео:Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

ОГЛАВЛЕНИЕ

1.1. ОБЩИЕ СВЕДЕНИЯ О СИСТЕМЕ MATLAB 2

1.2. Пакет Partial Differential Equations Toolbox MatLab 4

1.3. Уравнения математической физики . 5

2. Практическая часть 7

2. 1 . Постановка задачи 7

2. 2 . Решение задачи 7

3. Заключение 17

4. Список литературы 18

Микроэлектроника является одной из наиболее динамично развивающихся и востребованных отраслей науки и техники. Элементы современных СБИС и микрооптикоэлектромеханических систем (МОЭМС) представляют собой сложные структуры, в основу функционирования которых положены разнообразные физические эффекты. Разработка подобных элементов практически невозможна без решения уравнений математической физики, представляющих

собой, как правило, дифференциальные уравнения (ДУ) в частных производных.

Нахождение точного аналитического решения, к сожалению, возможно лишь для весьма ограниченного круга одномерных задач при использовании целого ряда допущений, негативно отражающихся на адекватности полученных результатов. Для решения задач математической физики в случае нескольких измерений необходимо использовать численные методы, позволяющие преобразовать дифференциальные уравнения или их системы в системы алгебраических уравнений. Для решения полученных нелинейных систем алгебраических

уравнений или линейных систем большой размерности используют итерационные методы. При этом одной из наиболее сложных проблем является обеспечение сходимости итерационного процесса, в значительной степени определяющей время вычислений. Точность решения определяется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера.

1. ОБЩИЕ СВЕДЕНИЯ О СИСТЕМЕ MATLAB

Название MATLAB является сокращением от Matrix Laboratory, и первоначально пакет MATLAB разрабатывался как средство доступа к библиотекам программ LINPACK и EISPACK, предназначенных для матричных вычислений. Пакет MATLAB создан компанией MathWorks около двадцати лет назад. Работа сотен ученых и программистов направлена на постоянное расширение его возможностей и совершенствование заложенных алгоритмов. В настоящее время MATLAB является мощным и универсальным средством решения задач, возникающих в различных областях человеческой деятельности. Спектр проблем, исследование которых может быть осуществлено при помощи MATLAB и его расширений (Toolbox), охватывает: матричный анализ, обработку сигналов и изображений, задачи математической физики, оптимизационные задачи, финансовые задачи, обработку и визуализацию данных, работу с картографическими изображениями, нейронные сети, нечеткую логику и многое другое. Около сорока специализированных Toolbox могут быть выборочно установлены вместе с MATLAB по желанию пользователя. В состав многих Toolbox входят приложения с графическим интерфейсом пользователя, которые обеспечивают быстрый и наглядный доступ к основным функциям. Пакет Simulink, поставляемый вместе с MATLAB, предназначен для интерактивного моделирования нелинейных динамических систем, состоящих из стандартных блоков.

Обширная и удобная справочная система MATLAB способна удовлетворить потребности как начинающего, так и достаточно опытного пользователя. Полная гипертекстовая информационная система (на английском языке) содержит описание встроенных функций и достаточно большое число примеров их использования. Ссылки позволяют переходить к разделам, имеющим отношение к изучаемому вопросу, что облегчает самостоятельный поиск интересующей информации. Доступ из командной строки к кратким сведениям о встроенных функциях обеспечивает возможность быстрого выбора нужного варианта обращения к функциям. Инженерам и научным работникам, проводящим самостоятельные исследования, оказываются полезными прилагаемые к пакету электронные книги в формате PDF. Данные книги не только дублируют справочную систему MATLAB и каждого Toolbox, но и содержат теоретические сведения и математическую базу, необходимые для осознанного использования описываемых, средств. Справочная система снабжена ссылками на книги и статьи, посвященные реализованным алгоритмам в MATLAB и Toolbox, что позволяет исследователю и разработчику собственных алгоритмов вникнуть в суть дела.

MATLAB обладает хорошо развитыми возможностями визуализации двумерных и трехмерных данных. Высокоуровневые графические функции призваны сократить усилия пользователя до минимума, обеспечивая, тем не менее, получение качественных результатов. Интерактивная среда для построения графиков позволяет обойтись бел графических функций для визуализации данных. Кроме того, она служит и для оформления результата желаемым образом: размещения поясняющих надписей, задания цвета и стиля линий и поверхностей, словом, для получения изображения, пригодного для включения в отчет или статью. Полный доступ к изменению свойств отображаемых графиков дают низкоуровневые функции, применение которых подразумевает понимание принципов компьютерной графики и владение приемами программирования.

В MATLAB реализованы классические численные алгоритмы решения уравнений, задач линейной алгебры, нахождения значений определенных интегралов, аппроксимации, решения систем или отдельных дифференциальных уравнений. Для применения базовых вычислительных возможностей достаточно знания основных численных методов в рамках программы технических вузов. Решение специальных задач, разумеется, невозможно без соответствующей теоретической подготовки; впрочем, сведения, изложенные в справочной системе, оказываются неоценимым подспорьем для желающих самостоятельно разобраться в обширных возможностях пакета MATLAB.

Простой встроенный язык программирования позволяет легко создавать собственные алгоритмы. Простота языка программирования компенсируется огромным множеством функций MATLAB и Toolbox. Данное сочетание позволяет достаточно быстро разрабатывать эффективные программы, направленные на решение практически важных задач.

Визуальная среда GUIDE предназначена для написания приложений с графическим интерфейсом пользователя. Работа в среде GUIDE проста, но предполагает владение основами программирования и дескрипторной графики. Наличие определенного навыка работы в среде GUIDE предоставляет возможность создать визуальную среду для проведения собственных исследований, что значительно облегчает работу и существенно экономит время.

Объектно-ориентированный подход, заложенный в основу MATLAB, обеспечивает современную эффективную технологию программирования. С учетом специфики решаемой задачи разработчик приложений MATLAB в дополнение к существующим классам имеет возможность создавать собственные со своими методами.

MATLAB прекрасно интегрируется со многими приложениями и средами программирования. Связь MATLAB и MS Word обеспечивает возможность написания в редакторе MS Word интерактивных документов, так называемых М-книг, основанных на специальном шаблоне. Пользователь, работающий с М-книгой, может запускать блоки команд MATLAB непосредственно из документа MS Word, причем результат выполнения команд отображается в М-книге. Данное средство прекрасно подходит для создания электронных отчетов и учебных пособий.

Надстройка MS Excel Link, поставляемая вместе с MATLAB, существенно расширяет возможности MS Excel, обеспечивая доступ пользователя к функциям MATLAB и Toolbox. Подготовка данных осуществляется непосредственно в электронных таблицах, а обращение к функциям производится либо из ячеек рабочего листа, либо в модуле, написанном на Visual Basic (VBA). MATLAB Builder for MS Excel позволяет реализовывать алгоритмы MATLAB в виде СОМ-объектов и использовать их в приложениях на VBA.

Информация, хранящаяся в базах данных многих популярных форматов, может быть импортирована в MATLAB, нужным образом обработана и исследована при помощи функций MATLAB, а затем экспортирована в какую-либо другую базу данных. Для обмена данными используются команды языка запросов SQL. Поддерживается, в частности, связь с Microsoft Access, Microsoft SQL Server, Oracle. Имеется приложение с графическим интерфейсом, которое облегчает работу пользователей, не знакомых с языком запросов SQL.

Символические вычисления в MATLAB основаны на библиотеке, являющейся ядром пакета Maple. Решение уравнений и систем, интегрирование и дифференцирование, вычисление пределов, разложение в ряд и суммирование рядов, поиск решения дифференциальных уравнений и систем, упрощение выражений — вот далеко не полный перечень возможностей MATLAB для проведения аналитических выкладок и расчетов. Поддерживаются вычисления с произвольной точностью. Пользователи, имеющие опыт работы в Maple, могут напрямую обращаться ко всем функциям данного пакета (кроме графических) и вызывать процедуры, написанные на встроенном языке Maple.

Программный интерфейс приложения (API) реализует связь среды MATLAB с программами, написанными на С, Fortran или Java. Библиотека программного интерфейса позволяет вызывать имеющиеся модули на С, Fortran или Java из среды или программ MATLAB, обращаться к функциям MATLAB из программ на С или Fortran, осуществлять обмен данными между приложениями MATLAB и другими программами. Средства MATLAB Builder for СОМ предназначены для преобразования программ MATLAB в СОМ-объекты, доступные в других приложениях.

Для разработки интернет-приложений MATLAB создан MATLAB Web Server, причем процесс создания приложения достаточно прост— кроме умения программировать в MATLAB требуется только знание основ HTML.

Подводя итог вышесказанному, можно сделать вывод, что начинающий пользователь MATLAB может в процессе работы совершенствовать свои знания как в области моделирования и численных методов, так и программирования, и визуализации данных. Огромным преимуществом MATLAB является открытость кода, что дает возможность опытным пользователям разбираться в запрограммированных алгоритмах и, при необходимости, изменять их. Впрочем, разнообразие набора функций MATLAB и Toolbox допускает решение большинства задач без каких-либо предварительных модификаций.

1. ПАКЕТ PARTIAL DIFFERENTIAL EQUATIONS TOOLBOX MATLAB

Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Весьма важный пакет прикладных программ, содержащий множество функций для решения систем дифференциальных уравнений в частных производных. Дает эффективные средства для решения таких систем уравнений, в том числе жестких. В пакете используется метод конечных элементов. Команды и графический интерфейс пакета могут быть использованы для математического моделирования уравнений в частных производных применительно к широкому классу инженерных и научных приложений, включая задачи сопротивления материалов, расчеты электромагнитных устройств, задачи тепломассопереноса и диффузии. Основные возможности пакета:

1. полноценный графический интерфейс для обработки уравнений с частными производными второго порядка;
2. автоматический и адаптивный выбор сетки;
3. задание граничных условий: Дирихле, Неймана и смешанных;
4. гибкая постановка задачи с использованием синтаксиса MATLAB ;
5. полностью автоматическое сеточное разбиение и выбор величины конечных элементов;
6. нелинейные и адаптивные расчетные схемы;
7. возможность визуализации полей различных параметров и функций решения, демонстрация принятого разбиения и анимационные эффекты.

Видео:Простейшие уравнения в частных производныхСкачать

Пакет интуитивно следует шести шагам решения PDE с помощью метода конечных элементов. Эти шаги и соответствующие режимы пакета таковы: определение геометрии (режим рисования), задание граничных условий (режим граничных условий), выбор коэффициентов, определяющих задачу (режим PDE ), дисркре-тизация конечных элементов (режим сетки), задание начальных условий и решение уравнений (режим решения), последующая обработка решения (режим графика).

1. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

Разработка и исследование значительной части элементов современных сверхбольших интегральных схем (СБИС) и микрооптикоэлектромеханических систем (МОЭМС) связаны с решением задач математической физики, к которым относят задачи теплопроводности, диффузии, электростатики и электродинамики, задачи о течении жидкости, о распределении плотности электрического тока в проводящей среде, задачи о деформациях твердых тел и многие другие. Подобные задачи описываются дифференциальными уравнениями в частных производных с дополнительными уравнениями, выражающими граничные и начальные условия. Нахождение точного аналитического решения, к сожалению, возможно лишь для весьма ограниченного круга одномерных задач при использовании целого ряда допущений. Для решения уравнений математической физики в случае нескольких измерений используют числен­ные методы, позволяющие преобразовать дифференциальные уравнения или их системы в системы алгебраических уравнений. Точность решения определяется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера. рядков. В общем случае линейное дифференциальное уравнение в частных производных второго порядка с n независимыми переменными имеет вид вещественные функции независимых переменных. Уравнение (1) всегда может быть приведено к одной из трех стандартных канонических форм. По соотношению значений Aαβ(x) уравнения относят к эллиптическим, параболическим или гиперболическим в точке x. В частности, для дифференциальных уравнений в частных производных второго порядка с двумя независимыми переменными x, y, которые могут быть представлены в виде тип ДУ определяется знаком выражения, называемого дискриминантом Если D(x, y) Если D(x, y) > 0, дифференциальное уравнение является гиперболическим в точке (x, y). Если коэффициенты Axx, Axy, Ayy постоянные и значение D не зависит от x, y, то в зависимости от знака D уравнение является полностью эллиптическим, гиперболическим или параболическим.

1. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ

Метод конечных элементов – численный метод решения диф. уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твердого тела (сопромата), теплообмена, гидродинамики и электродинамики.

Предположим, что состояние системы описывается некоторой функцией. Пусть эта функция является единственным решением математической задачи, сформулированной на основе физических законов. Решение состояние в отыскании из бесконечного множества функций такой, которая удовлетворяет уравнениям задачи. Если задача достаточно сложная, то ее точное решение невозможно. Вместо того чтобы искать требуемую функцию среди бесконечного множества разнообразных функций, задача упрощается. Рассматривается некоторое семейство функций, определяемых конечным числом параметров. Как правило, среди таких функций нет точного решения задачи. Однако соответствующим подбором параметров можно попытаться приближенно удовлетворить уравнениям задачи и тем самым построить ее приближенное значение. Такой общий подход характерен для многих приближенных методов. Специфическим в методе конечных элементов является построение семейства функций, определяемых конечным числом параметров.

Допустим, требуется построить семейство функций u ( x ) при a # x # b . Интервал ab разбивается на конечное число частей (элементов), соединяющихся между собой и с концами интервала в узловатых точках x i . В пределах каждого элемента задается функция, например в виде линейного полинома. Она определяется своими значениями u ( x i ) в узлах на концах элемента. Если отыскиваемая функция является непрерывной, то значения ее в каждом узле для соседних элементов совпадают. В результате имеем семейство кусочно-линейных непрерывных функций, которые изображаются в виде ломаных и определяются конечным числом параметров – своими узловыми значениями.

В случае нескольких переменных схема метода конечных элементов в принципе не меняется. Таким образом, метод конечных элементов заменяет задачу отыскания функции на задачу отыскания конечного числа ее приближенных значений в отдельных точках-узлах. При этом если исходная задача относительно функции состоит из функционального уравнения, например диф. уравнения с соответствующими граничными условиями, то задача метода конечных элементов относительно ее значений в узлах представляет собой систему алгебраических уравнений.

С уменьшением максимального размера элементов увеличивается число узлов и неизвестных узловых параметров. Вместе с этим повышается возможность более точно удовлетворить уравнениям задачи и тем самым приблизиться к искомому решению. В настоящее время уже изучены многие вопросы, качающиеся сходимости приближенного решения методом конечных элементов к точному. Для линейных задач, когда неизвестные функции и операции над ними входят во все соотношения задачи только в первой степени, метод конечных элементов получил достаточно полное математическое обоснование. Отметим несколько важных достоинств метода конечных элементов.

Метод конечных элементов позволяет построить удобную схему формирования системы алгебраических уравнений относительно узловых значений искомой функции. Приближенная аппроксимация решения при помощи простых полиномиальных функций и все необходимые операции выполняются на отдельном типовом элементе. Затем производится объединение элементов, что приводит к требуемой системе алгебраических уравнений. Такой алгоритм перехода от отдельного элемента к их полному набору особенно удобен для геометрически и физически сложных систем.

Каждое отдельное алгебраическое уравнение, полученное на основе метода конечных элементов, содержит незначительную часть узловых неизвестных от общего их числа. Другими словами, многие коэффициенты в уравнениях алгебраической системы равны нулю, что значительно облегчает ее решение.

Задачи, решение которых описывается функциями, удовлетворяющими функциональным уравнениям, носят название континуальных. В отличие от них решение так называемых дискретных задач точно определяется конечным числом параметров, удовлетворяющих соответствующей системе алгебраических уравнений. Метод конечных элементов. так же как и другие численные методы, по существу приближенно заменяет континуальную задачу на дискретную. В методе конечных элементов вся процедура такой замены имеет простой физический смысл. Это позволяет более полно представить себе весь процесс решения задачи, избежать многих возможных ошибок и правильно оценить получаемые результаты.

Помимо континуальных задач схема метода конечных элементов применяется для соединения элементов и формирования алгебраических уравнений при решении непосредственно дискретных задач. Это расширяет сферу применения метода.

Поперечная деформация мембраны ω определяется уравнением , где p — давление, Т – напряжение, отнесенное к единице длины. При относительно малых деформациях напряжение в мембране можно считать постоянным. При Т=10 7 Н/м и p =10 4 Па создать программу для расчета прогиба мембраны, представленной на рисунке.

— изгибная жесткость, где Е – модуль упругости, t – толщина пластинки, ν — коэффициент Пуассона.

Схема решения данной задачи в MATLAB состоит из следующих этапов:

1. Применение пакета MATLAB для решения дифференциальных уравнений в частных производных.
2. Для расчета прогиба пластины необходимо использовать приложение PDEtool .

Для решения ДУЧП определили по заданным условиям, чему равна правая часть уравнения, которая в данной задаче является константой:

Работа в PDEtool :

Запуск приложения осуществляется командой pdetool. При этом на экране монитора отображается главное окно приложения.

Для задания прямоугольной области решения необходимо активизировать с помощью «мыши» кнопку с символом  , после чего навести курсор «мыши» на рабочее поле редактора, нажать левую кнопку «мыши» в левом верхнем углу (0, 1) задаваемой прямоугольной области, переместить курсор в правый нижний угол (0, −1) области, удерживая левую кнопку, после чего отпустить ее. Прямоугольная область будет зафиксирована.

При необходимости корректировки координат и размеров области нужно навести курсор «мыши» на изображение прямоугольника и дважды щелкнуть левой кнопкой. На экране появится окно редактирования параметров области с соответствующими полями. В первом и втором полях отображаются координаты левой нижней точки прямоугольника по осям х и

y соответственно. В третьем поле – ширина прямоугольника, в четвертом – высота, в пятом – условное обозначение. Области решения произвольной формы могут быть заданы аналогичным образом с использованием кнопок, имеющих изображения прямоугольников, эллипсов и полигона. При этом результирующая область может быть определена как объединение или разность нескольких областей простой формы. Для этого в поле Set formula указываются условные обозначения областей, связанные знаком «+» в случае объединения или знаком «−» в случае разности.

Создадим второй квадрат со стороной 0,5 и разместим его в правом нижнем углу квадрата R 1

В поле Set formula записали формулу R 1- R 2 и получили пластину требуемых размеров

Для задания граничных условий необходимо активизировать манипулятором «мышь» кнопку с символом ∂ Ω, в результате чего окно приложения примет вид, показанный на рисунке; (т.к. все края пластины закреплены, поперечная деформация там будет равна 0;

Для редактирования вида дифференциального уравнения и ввода его функций и коэффициентов необходимо активизировать манипулятором «мышь» кнопку с символами PDE, после чего внести соответствующие изменения в полях окна редактирования, показанного на рисунке

Формирование триангулярной сетки осуществляется за счет активизации кнопки с символом ∆. При необходимости увеличения числа узлов сетки следует активизировать кнопку

Решение задачи осуществляется при активизации кнопки с символом «=». По умолчанию значения функции решения выделяются различными цветами.

Для графического вывода решения задачи в виде трехмерного (3D) изображения следует активизировать кнопку , после чего в появившемся окне редактирования параметров изображения внести в соответствующие поля данные, как показано на рисунке

При активизации кнопки Plot на экран будет выведен график, показанный на рисунке

pdetool( ‘appl_cb’ ,1);

set(ax, ‘DataAspectRatio’ ,[1 1 1]);

set(ax, ‘PlotBoxAspectRatio’ ,[1.5 1 1]);

set(ax, ‘XLim’ ,[-1.5 1.5]);

set(ax, ‘XTickMode’ , ‘auto’ );

set(ax, ‘YTickMode’ , ‘auto’ );

pderect([0 1 0 -1], ‘R1’ );

pderect([0.5 1 -0.5 -1], ‘R2’ );

set(findobj(get(pde_fig, ‘Children’ ), ‘Tag’ , ‘PDEEval’ ), ‘String’ , ‘R1-R2’ )

Видео:Линейные дифференциальные уравнения в частных производныхСкачать

MatLab: решение дифференциальных уравнений

Дата добавления: 2015-06-12 ; просмотров: 11953 ; Нарушение авторских прав

Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, ее производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением.

Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.

Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные y‘(x),y»(x). y (n) (x) до порядка n включительно и удовлетворяющая этому уравнению.

Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных.

Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида

или ,

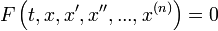
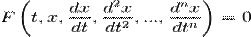
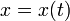
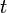
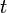
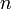
где — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от переменной времени , штрих означает дифференцирование по . Число называется порядком дифференциального уравнения.

Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:

,

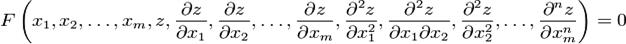
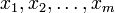
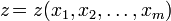
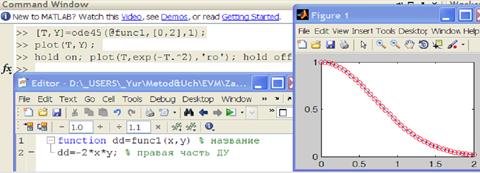
где — независимые переменные, а — функция этих переменных.

Простой пример решения ДУ в MatLab:

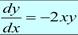
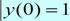
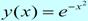
В качестве самого простого примера приведем решение следующего уравнения с начальным условием и аналитическим решением .

Возможный формат вызова процедуры решателя в MatLab:

Снимок экрана, который соответствует численному решению этой задачи в системе MatLab.

Файл-функция, описывающая правую часть уравнения, – текстовый файл с расширением func1.m – содержит всего две строки

Знаком % начинаются комментарии. Вызываться такая функция может из другойпрограммы, функции, или, как в этом случае, из командного окна

Здесь задан временной интервал от Tstart=0 до Tfinal=2 и начальное значение функции StartVector=1. График полученной таким образом функции Y(T) воспроизводится вызовом встроенной функции plot

Следующей строкой мы кружочками нарисовали на том же графике точное решение в точках полученного вектора-столбца T:

В общем случае, процедура ode45 может решать систему уравнений следующего вида:

функция-столбец, зависящая отвремени и компонент вектора x.

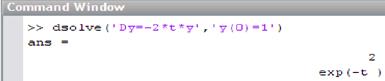
Заметим, что уравнение (1) можно решить в MatLab и символьно. Приведем часть командного окна, где была вызвана стандартная процедура dsolve

Здесь также использовано начальное условие.

Видим, что с точностью до переобозначения x → t результат совпадает с приведенным выше.

📽️ Видео

Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

8 Дифференциальные уравнения в частных производных MathcadСкачать

Решение дифференциальных уравнений и систем. Урок 150Скачать

Найти общее решение уравнения в частных производных первого порядка.Скачать

MatLab. 7.9. Системы дифференциальных уравненийСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

MatLab. 9.5g. Решение дифференциальных уравнений – dsolveСкачать

5 Численное решение дифференциальных уравнений Part 1Скачать

Работа в MATLAB. МКР. Задача КошиСкачать

Уравнения в частных производных первого порядка| poporyadku.schoolСкачать

Символьные и численные расчеты в MATLABСкачать