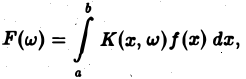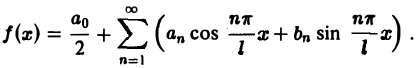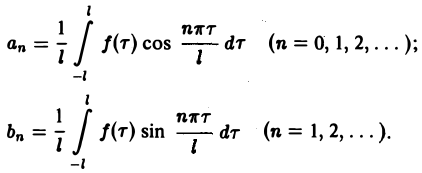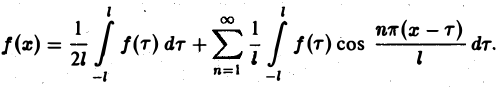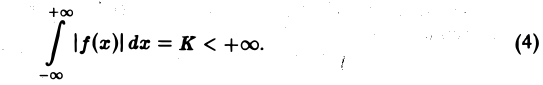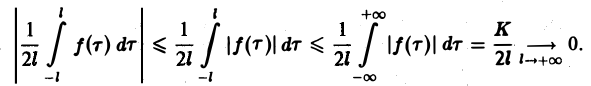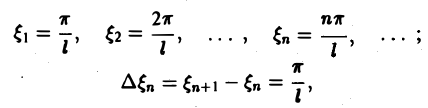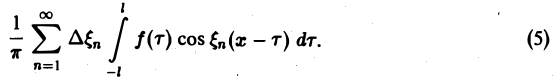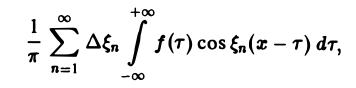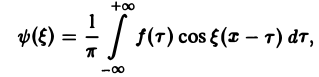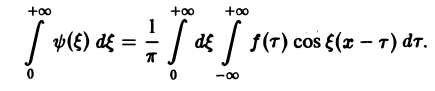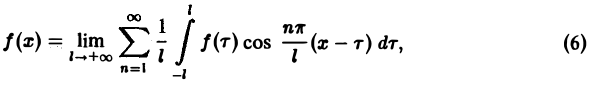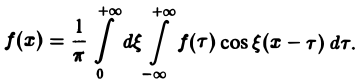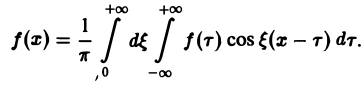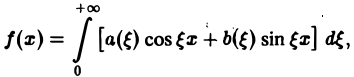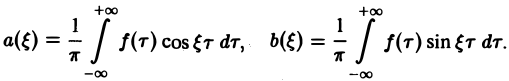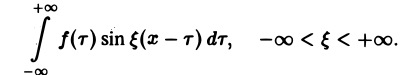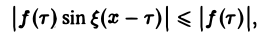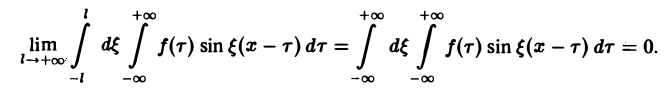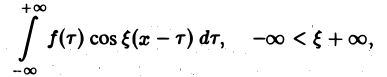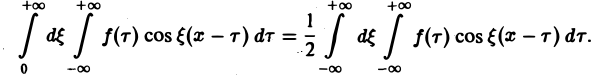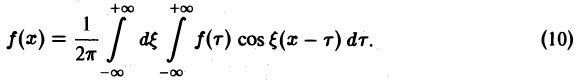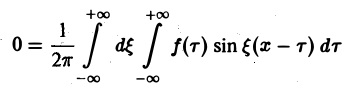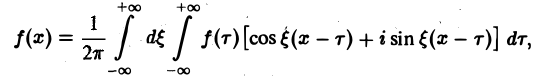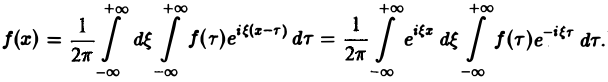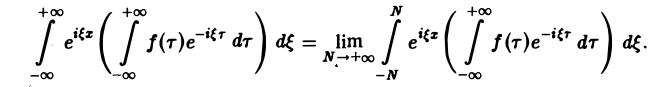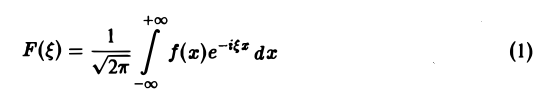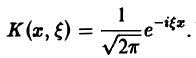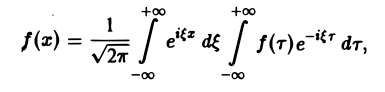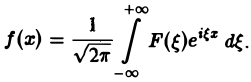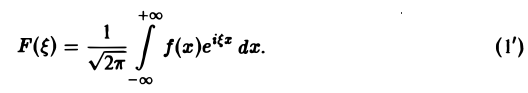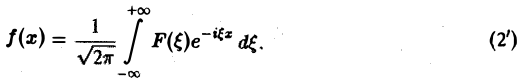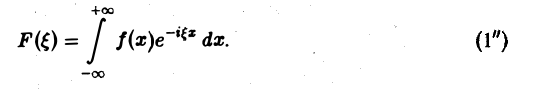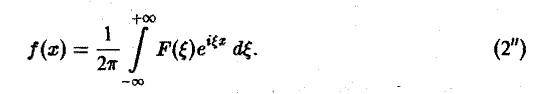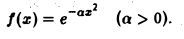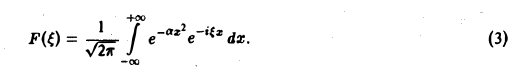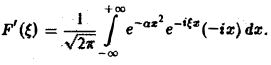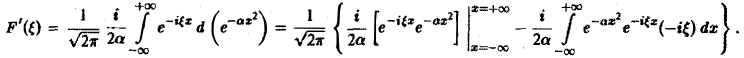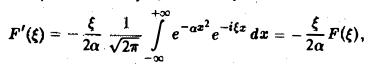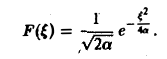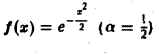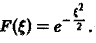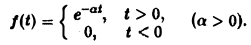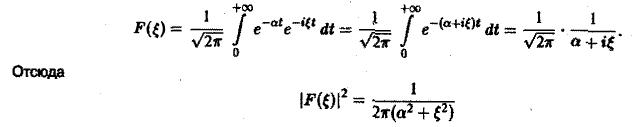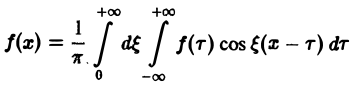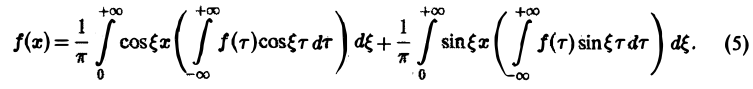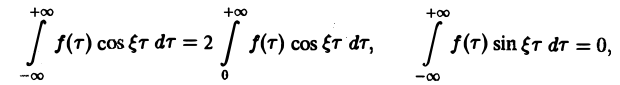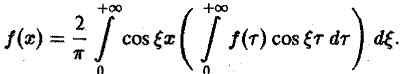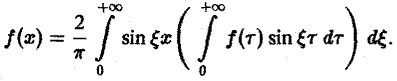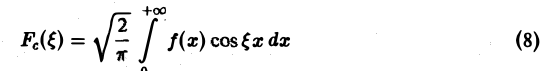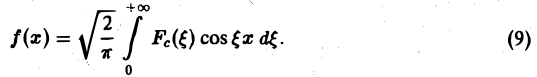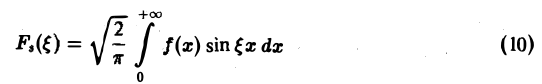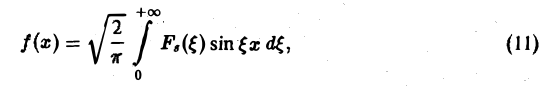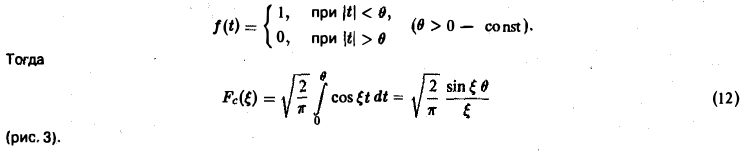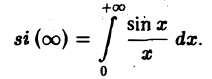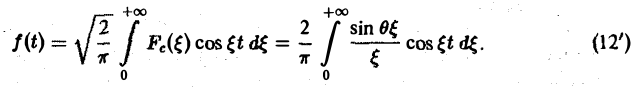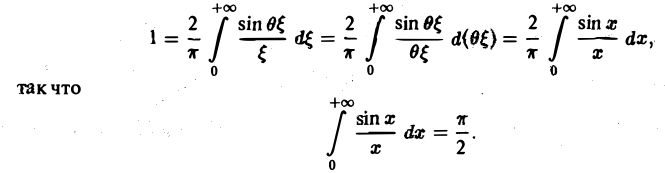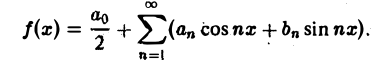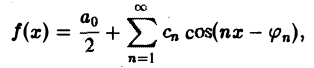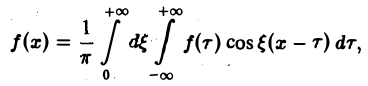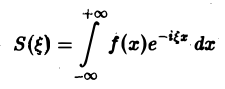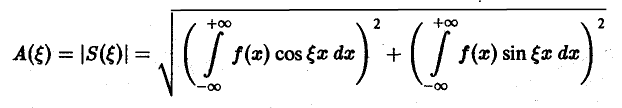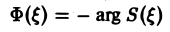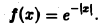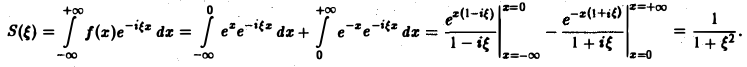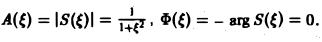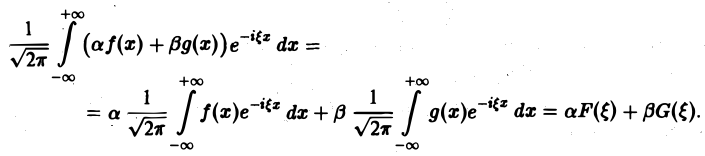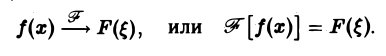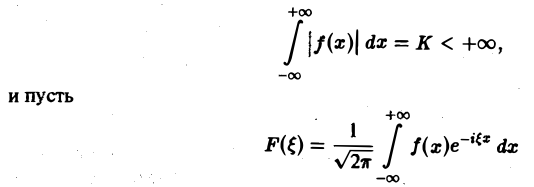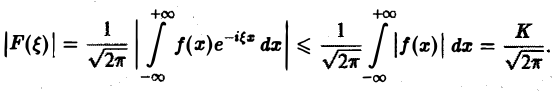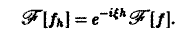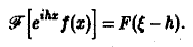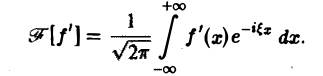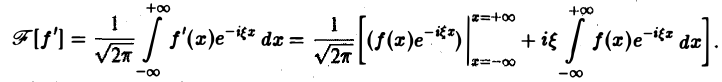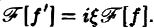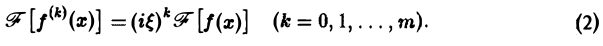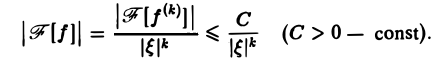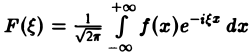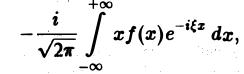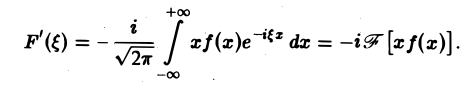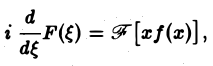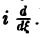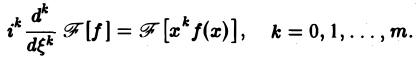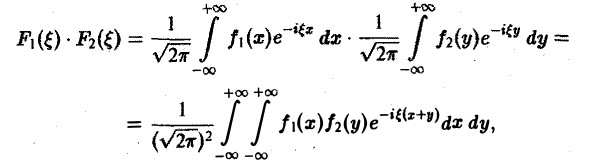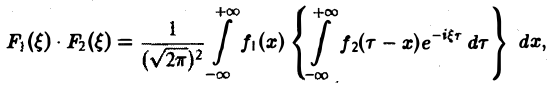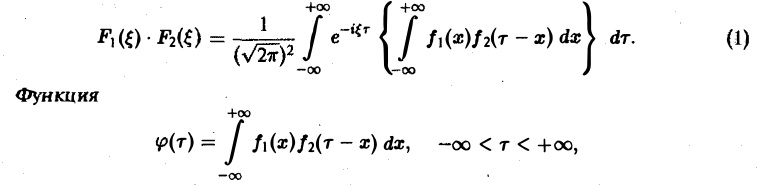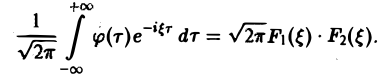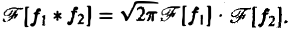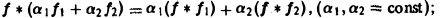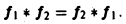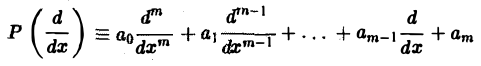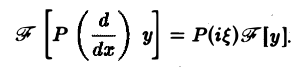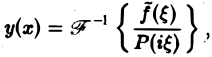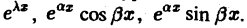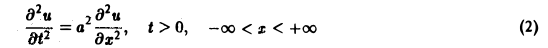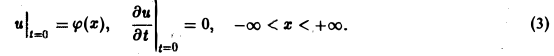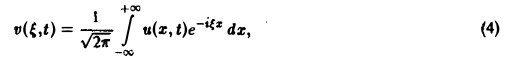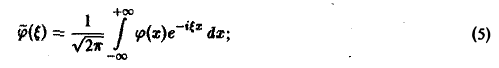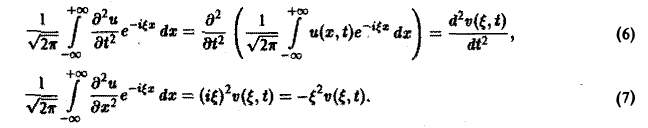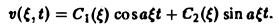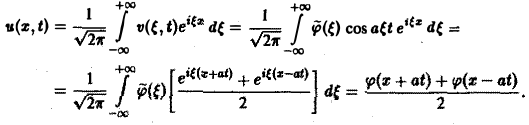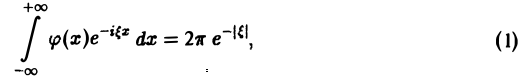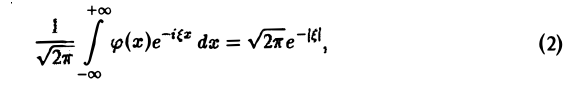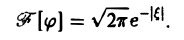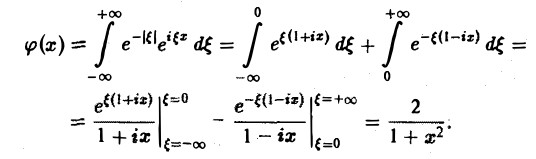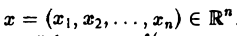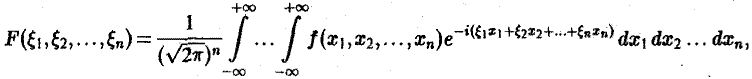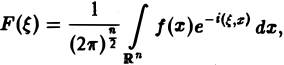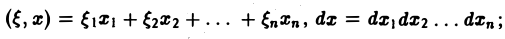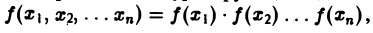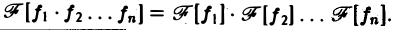Одним из мощных средств исследования задач математической физики является метод интегральных преобразований.
Пусть функция f(x) задана на интервале (а, 6), конечном или бесконечном. Интегральным преобразованием функции f(х) называется функция (*)
где К(х, w) — фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существует в собственном или несобственном смысле).
- Интеграл Фурье
- Комплексная форма интеграла Фурье
- Преобразование Фурье. Косинус- и синус-преобразования Фурье
- Косинус- и синус-преобразования Фурье
- Амплитудный и фазовый спектры интеграла Фурье
- Свойства преобразования Фурье
- Приложения преобразования Фурье
- Понятие о многомерном преобразовании Фурье
- Дополнение к преобразованию Фурье
- Преобразование Фурье. Интеграл Фурье. Комплексная форма интеграла
- Теорема 1:
- Пример 3 прамоугольный импульс:
- Пример 4:
- Фурье-вычисления для сравнения изображений
- Постановка задачи
- образец
- в изображении
- Корреляция как мера между изображениями
- Свёртка двух функций
- Преобразование Фурье
- Многомерное преобразование Фурье
- Дискретное преобразование Фурье
- Формулы дискретных преобразований
- Фурье-преобразования для вычисления свёртки
- Фурье-преобразования для вычисления корреляции
- Фурье-преобразования для решения задачи
- Упрощение формул для решения поставленной задачи
- Алгоритм поиска фрагмента в полном изображении
- Примеры реализации
Видео:Курс по ИДУ: Применение ИПФ к решению интегральных и дифференциальных уравнений | Занятие 10Скачать

Интеграл Фурье
Всякая функция f(x), которая на отрезке [— l, l] удовлетворяет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом (1)
Коэффициенты аn и bn ряда (1) определяются по формулам Эйлера—Фурье:
(2)
Ряд в правой части равенства (1) можно записать в иной форме. С этой целью внесем в него из формул (2) значения коэффициентов аn и bn, подведем под знаки интегралов cos 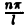
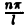
(3)
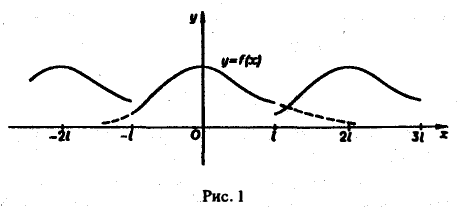
Если функция f(x) первоначально была определена на интервале числовой оси, большем, чем отрезок [-l, l] (например, на всей оси), то разложение (3) воспроизведет значения этой функции только на отрезке [-l, l] и продолжит ее на всю числовую ось как периодическую функцию с периодом 2l (рис. 1).
Поэтому, если функция f(x) (вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно попытаться перейти к пределу при l → +∞. При этом естественно потребовать выполнения следующих условий:
1, f(x) удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох;
2. функция f(x) абсолютно интегрируема на всей числовой оси,
При выполнении условия 2 первое слагаемое правой части равенства (3) при l → +∞ стремится к нулю. В самом деле,
Попытаемся установить, во что перейдет в пределе при l → +∞ сумма в правой части (3). Положим
так, что 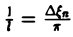
В силу абсолютной сходимости интеграла эта сумма при больших l мало отличается от выражения
которое напоминает интегральную сумму для функции переменного ξ
составленную для интервала (0, + ∞) изменения Поэтому естественно ожидать, что при l → +∞ ( 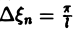
С другой стороны, при l → +∞ (х фиксировано) из формулы (3) вытекает, что
и мы получаем равенство
(7)
Достаточное условие справедливости формулы (7) выражается следующей теоремой.
Теорема:
Если функция f(x) абсолютно интегрируема на всей числовой оси — ∞
При этом во всякой точке xq, являющейся точкой разрыва 1-го рода функции f(x), значение интеграла в правой части (7) равно
Формулу (7) называют интегральной формулой Фурье, а стоящий в ее правой части интеграл — интегралам Фурье.
Если воспользоваться формулой для косинуса разности, то формулу (7) можно записать в виде (8)
Функции а( ξ ), b( ξ ) являются аналогами соответствующих коэффициентов Фурье an и bn 2π-периодической функции, но последние определены для дискретных значений п, в то время как а( ξ ), b( ξ ) определены для непрерывных значений ξ ∈ (— ∞, + ∞).
Видео:AGalilov: Преобразование Фурье "на пальцах"Скачать
Комплексная форма интеграла Фурье
Предполагая f(x) абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл
Этот интеграл равномерно сходится для — ∞
и потому представляет собой непрерывную и, очевидно, нечетную функцию от ξ. Но тогда
С другой стороны, интеграл
есть четная функция переменной так что
Поэтому интегральную формулу Фурье можно записать так:
на мнимую единицу i и прибавим к равенству (10). Получим
откуда, в силу формулы Эйлера (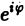
(11)
Это — комплексная форма интеграла Фурье. Здесь внешнее интегрирование по ξ понимается в смысле главного значения по Коши:
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Преобразование Фурье. Косинус- и синус-преобразования Фурье
Пусть функция f(x) является кусочно-гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси.
Определение:
называется преобразованием Фурье функции f(x) (спектральной функцией).
Это — интегральное преобразование функции f(x) на интервале (- ∞ ,+ ∞) с ядром
Используя интегральную формулу Фурье
Это так называемое обратное преобразование Фурье, дающее переход от F( ξ ) к f(x). Иногда прямое преобразование Фурье задают так:
Тогда обратное преобразование Фурье определится формулой
Преобразование Фурье F( ξ ) функции f(х) определяют также следующим образом:
Тогда, в свою очередь,
При этом положение множителя 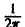
Пример:
Найти преобразование Фурье функции
Это равенство допускает дифференцирование по ξ под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда ξ принадлежит любому конечному отрезку):
Интегрируя по частям, будем иметь
Внеинтегральное слагаемое обращается в нуль, и мы получаем
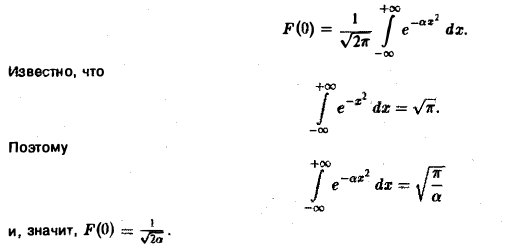
(С — постоянная интегрирования). Полагая в (4) ξ = 0, найдем С —F(0). В силу (3) имеем
В частности, для
Пример:
Разряд конденсатора через сопротивление. Рассмотрим функцию
Для спектральной функции F( ξ ) получаем
Условие абсолютной интегрируемости функции f(x) на всей числовой оси является весьма жестким. Оно исключает, например, такие элементарные функции, как f(x) = 1. f(x) = x 3 , f(х) = cosx, f(х) = е х , для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует.
Фурье-образ имеют только те функции, которые достаточно быстро стремятся к нулю при |х| → + ∞ (как в примерах 1 и 2).
Видео:Интеграл Фурье и преобразование ФурьеСкачать

Косинус- и синус-преобразования Фурье
Используя формулу косинуса, разности, перепишем интегральную формулу Фурье
в следующем виде:
Пусть f(x) — четная функция. Тогда
так что из равенства (5) имеем
(6)
В случае нечетной f(x) аналогично получаем
(7)
Если f(х) задана лишь на (0, + ∞), то формула (6) продолжает f(x) на всю ось Ох четным образом, а формула (7) — нечетным.
Определение:
называется косинус-преобразованием Фурье функции f(x). Из (6) следует, что для четной функции f(x)
Это означает, что f(x), в свою очередь, является косинус-преобразованием для Fc( ξ ). Иными словами, функции f и Fc являются взаимными косинус-преобразованиями.
Определение:
называется синус-преобразованием Фурье функции f(x).
Из (7) получаем, что для нечетной функции f(х)
т.е. f и Fs являются взаимными синус-преобразованиями.
Пример:
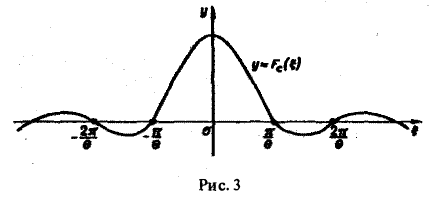
Прямоугольный импульс. Пусть f(t) — четнaя функция, определенная следующим образом:
Воспользуемся полученным результатом для вычисления интеграла
В силу формулы (9) имеем
В точке t = 0 функция f(t) непрерывна и равна единице.
Поэтому из (12′) получим
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Амплитудный и фазовый спектры интеграла Фурье
Пусть периодическая с периодом 2π функция f(х) разлагается в ряд Фурье
Это равенство можно записать в виде
где Cn = 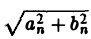
Для непериодической функции f(x), заданной на (- ∞, + ∞), при определенных условиях оказывается возможным представить ее интегралом Фурье
осуществляющим разложение этой функции по всем частотам 0
(прямое преобразование Фурье функции f(х)).
называется амплитудным спектром, а функция
(0 — фазовым спектром функции f(x).
Амплитудный спектр A (ξ) служит мерой вклада частоты ξ в функцию f(х).
Пример:
Найти амплитудный и фазовый спектры функции
Находим спектральную функцию
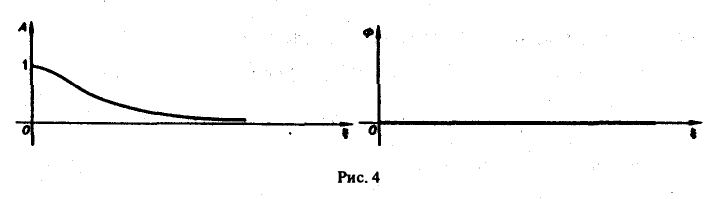
Графики этих функций изображены на рис. 4.
Видео:Дифференциальные уравнения | ряды Фурье Бесселя | 1Скачать

Свойства преобразования Фурье
1, Линейность. Если F( ξ ) и G( ξ ) — преобразования Фурье функций f(х) и g(х) соответственно, то при любых постоянных а и β преобразованием Фурье функции а f(х) + β g(х) будет функция a F( ξ ) + βG( ξ ).
Пользуясь свойством линейности интеграла, имеем
Таким образом, преобразование Фурье есть линейный оператор. Обозначая его через 
Если F( ξ ) есть преобразование Фурье абсолютно интегрируемой на всей числовой оси функции f(х), то F( ξ ) ограничена при всех ξ ∈ (— ∞, + ∞).
Пусть функция f(х) абсолютно интегрируема на всей оси — ∞
— преобразование Фурье функции f(х). Тогда
Задача:
Пусть f(x) — функция, допускающая преобразование Фурье, h — действительное число. Функция fh(x) = f(x-h) называется сдвигом функции f(x). Пользуясь определением преобразования Фурье, показать, что
Задача:
Пусть функция f(x) имеет преобразование Фурье F( ξ ), h — действительное число. Показать, что
3. Преобразование Фурье и операция дифференцирования. Пусть абсолютно интегрируемая функция f(х) имеет производную f'(х), также абсолютно интегрируемую на всей оси Ох, так что f(х) стремится к нулю при |х| —► + ∞. Считая f'(х) гладкой функцией, запишем
Интегрируя по частям, будем иметь
Внеинтегральное слагаемое обращается в нуль (так как f(х) → 0 при |х| → + ∞), и мы получаем (1)
Таким образом, дифференцированию функции f(х) отвечает умножение ее образа Фурье 
Если функция f(х) имеет гладкие абсолютно интегрируемые производные до порядка m включительно и все они, как и сама функция f(х), стремятся к нулю при |x| → + ∞, то, интегрируя по частям нужное число раз, получим
Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину iξ и тем самым упрощает задачу интегрирования некоторых видов дифференциальных уравнений.
Так как преобразование Фурье 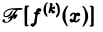
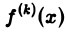

Из этой оценки следует: чем больше функция f(х) имеет абсолютно интегрируемых производных, тем быстрее ее преобразование Фурье стремится к нулю при | ξ | → + ∞.
Замечание:
Условие 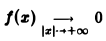
4. Связь между скоростью убывания функции f(x) при |х| → + ∞ и гладкостью ее преобразования Фурье. Предположим, что не только f(x), но и ее произведение хf(х) является абсолютно интегрируемой функцией на всей оси Ох. Тогда преобразование Фурье
функции f(x) будет дифференцируемой функцией.
Действительно, формальное дифференцирование по параметру ξ подынтегральной функции приводит к интегралу
который является абсолютно и равномерно сходящимся относительно параметра Следовательно, дифференцирование возможно, и
т. е. операция умножения f(х) на аргумент х переходит после преобразования Фурье в операцию
Если вместе с функцией f(х) абсолютно интегрируемыми на всей оси Ох являются функции хf(х)…..х m f(х), то процесс дифференцирования можно продолжить.
Получим, что функция F( ξ ) = 
Таким образом, чем быстрее функция f(х) убывает при |х| → + ∞, тем более гладкой получается функция F( ξ ) = 
Теорема:
О свертке. Пусть F1( ξ ) и F2( ξ ) — преобразования Фурье функций f1(x) и f2(x) соответственно. Тогда
причем двойной интеграл в правой части сходится абсолютно.
Положим х + у = т, так что у = т — х. Тогда будем иметь
или, меняя порядок интегрирования,
называется сверткой функций f(x) и f2(x) и обозначается символом 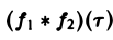
Отсюда видно, что преобразование Фурье свертки функций f1(x) и f2(x) равно умноженному на 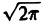
Замечание:
Нетрудно установить следующие свойства свертки:
Видео:Решение дифференциальных уравнений ДИФФУРЫСкачать

Приложения преобразования Фурье
1, Пусть 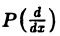
(аo, a1,… ,ат = const). Используя формулу для преобразования Фурье производных функции у(х), находим
Рассмотрим дифференциальное уравнение
где 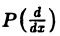
Предположим, что искомое решение у(х) имеет преобразование Фурье y(ξ), а функция f(x) имеет преобразование f( ξ ). Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси Oξ относительно y(ξ)
так что формально
где символ 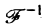
Основное ограничение применимости этого метода связано со следующим фактом. Решение обыкновенного дифференциального уравнения с постоянными коэффициентами содержит функции вида
Они не являются абсолютно интегрируемыми на оси — ∞
(а = const), при начальных условиях
Это — задача о свободных колебаниях бесконечной однородной струны, когда задано начальное отклонение φ(х) точек струны, а начальные скорости отсутствуют.
Поскольку пространственная переменная х изменяется в пределах от — ∞ до + ∞, подвергнем уравнение и начальные условия преобразованию Фурье по переменной х. Будем предполагать, что
1) функции u(z, t) и φ(x) — достаточно гладкие и стремятся к нулю при х → + ∞ и ∀t ≥ О настолько быстро, что существуют преобразования Фурье
2) допустимы операции дифференцирования, так что
Умножая обе части (2) на 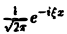
а из начальных условий (3) найдем
Таким образом, применяя к задаче (2)-(3) преобразование Фурье, приходим к задаче Коши (8)—(10) для обыкновенного дифференциального уравнения, где ξ — параметр. Решением уравнения (8) является функция
Из условий (9) и (10) находим, что С1( ξ ) = φ( ξ ). C2( ξ ) = 0, так что v( ξ, t) = φ( ξ )cos aξt. Применяя обратное преобразование Фурье, получим
Это частный случай формулы Даламбера решения задачи (2)-(3).
2. Преобразование Фурье может быть использовано при решении некоторых интегральных уравнений, т. е. уравнений, в которых неизвестная функция входит под знак интеграла.
Рассмотрим, например, уравнение
где φ(х) — искомая функция. Записав (1) в виде
замечаем, что левую часть (2) можно рассматривать как преобразование Фурье функции φ(х), так что (2) равносильно следующему равенству:
Тогда по формуле обращения
Функция 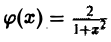
Видео:Метод Лапласа решения ДУСкачать

Понятие о многомерном преобразовании Фурье
Преобразование Фурье:
Многомерным преобразованием Фурье абсолютно интегрируемой функции f(х1, х2,…, хb) называется функция
символ 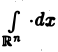
Свойства многомерного преобразования аналогичны соответствующим свойствам преобразования Фурье функции одной переменной. В специальном случае, когда
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Дополнение к преобразованию Фурье


Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Решение физических задач с помощью дифференциальных уравненийСкачать

Преобразование Фурье. Интеграл Фурье. Комплексная форма интеграла
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
исследования задач математической физики является метод интегральных преобразований. Пусть функция f(x) задана на интервале (а, 6), конечном или бесконечном. Интегральным преобразованием функции f(x) называется функция где К(х, ш) — фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существуете собственном или несобственном смысле). §1.
Интеграл Фурье Всякая функция f(x), которая на отрезке [-f, I] удовлетворяет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом Коэффициенты а*, и 6„ ряда (1) определяются по формулам Эйлера—Фурье: ПРЕОБРАЗОВАНИЕ ФУРЬЕ Интеграл Фурье Комплексная форма интеграла Преобразование Фурье Косинус и синус преобразования Амплитудный и фазовый спектры Свойства Приложения Ряд в правой части равенства (1) можно записать в иной форме.
С этой целью внесем в него из формул (2) значения коэффициентов а» и оп, подведем под знаки интегралов cos ^ х и sin х (что возможно, поскольку переменной интегрирования является т) О) и используем формулу для косинуса разности. Будем иметь Если функция/(ж) первоначально была определена на интервале числовой оси, большем, чем отрезок [-1,1] (например, на всей оси), то разложение (3) воспроизведет значения этой функции только на отрезке [-1,1] и продолжит се на всю числовую ось как периодическую функцию с периодом 21 (рис. 1).
Поэтому, если функция f(x) (вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно попытаться перейти к пределу при I +оо. При этом естественно потребовать выполнения следующих условий: 1. f(x) удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох 2. функция f(x) абсолютно интегрируема на всей числовой оси, При выполнении условия 2 первое слагаемое правой части равенства (3) при I -* +оо стремится к нулю. В самом деле, Попытаемся установить, во что перейдет в пределе при I +оо сумма в правой, части (3).
Возможно вам будут полезны данные страницы:
Положим так, что Тогда сумма в правой части (3) примет вид В силу абсолютной сходимости интеграла эта сумма при больших I мало отличается от выражения которое напоминает интегральную сумму для функции переменного £ составленную для интервала (0, +оо) изменения Поэтому естественно ожидать, что при сумма (5) перейдет в интеграл Сдругой стороны, при фиксировано) из формулы (3) вытекает, что и мы получаем равенство Достаточное условие справедливости формулы (7) выражается следующей теоремой.
Теорема 1:
Если функция f(x) абсолютно интегрируема на всей числовой оси и имеет вместе со своей производной конечное число точек разрыва первого рода на любом отрезке [а, 6], то справедливо равенство При этом во всякой точке xq, являющейся точкой разрыва 1-го рода функции /(ж), значение интеграла в правой части (7) равно Формулу (7) называют интегральной формулой Фурье, а стоящий в ее правой части интеграл — интегралом Фурье.
Если воспользоваться формулой дня косинуса разности, то формулу (7) можно записать в виде Функции а(£), Ь(£) являются аналогами соответствующих коэффициентов Фурье ап и Ьп 2тг-периодической функции, но последние определены для дискретных значений п, вто время как а(0> НО определеныдля непрерывных значений £ G (-оо, +оо). Комплексная форма интеграла Фурье Предполагая /(х) абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл Этот интеграл равномерно сходится для , так как и потому представляет собой непрерывную и, очевидно, нечетную функцию от Но тогда С другой стороны, интеграл есть четная функция переменной так что Поэтому интегральную формулу Фурье можно записать так: Умножим равенство на мнимую единицу i и прибавим к равенству (10).
Получим откуда, в силу формулы Эйлера будем иметь Это — комплексная форма интеграла Фурье. Здесь внешнее интегрирование по £ понимается в смысле главного значения по Коши: §2. Преобразование Фурье. Косинус- и синус-преобразования Фурье Пусть функция f(x) является кусочно-гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси. Определение. Функция откуда, в силу формулы Эйлера , будем иметь называется преобразованием Фурье функции /(г) (спектральной функцией).
Это — интегральное преобразование функции /(г) на интервале (-оо,+оо) с ядром Используя интегральную формулу Фурье получаем Это так называемое обратное преобразование Фурье, дающее переход от F(£) к /(х). Иногда прямое преобразование Фурье задают так: Тогда обратное преобразование Фурье определится формулой Преобразование Фурье функции /(ж) определяют также следующим образом: ПРЕОБРАЗОВАНИЕ ФУРЬЕ Интеграл Фурье Комплексная форма интеграла Преобразование Фурье Косинус и синус преобразования Амплитудный и фазовый спектры Свойства Приложения.
Тогда, в свою очередь, При этом положение множителя ^ достаточно произвольно: он может входить либо в формулу (1″), либо в формулу (2″).
Пример 1. Найти преобразование Фурье функции -4 Имеем Это равенство допуска ет дифференцирование по £ под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда < принадлежит любому конечному отрезку): Интегрируя по частям, будем иметь Внеинтегральное слагаемое обращается в нуль, и мы получаем откуда (С — постоянная интегрирования).
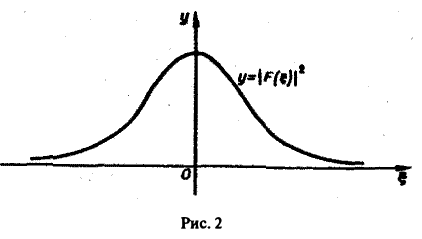
Полагая в (4) £ = 0, найдем С = F(0). В силу (3) имеем Известно, что В частности, для ) получаем, что Пример 2 (разред кокдемсетора через сопропиление). Рассмотрим функцию 4 Для спектрам ыюй функции F(£) получаем Отсюда (рис.2). Условие абсолютной интегри-руемости функции f(x) на всей числовой оси является весьма жестким. Оно исключает, например, такие элементарные функции, как ) = cos ж, f(x) = е1, для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует.
Фурье-образ имеют только те функции, которые достаточно быстро стремятся к нулю при |х| -+ +оо (как в примерах 1 и 2). 2.1. Косинус- и синус-преобразования Фурье Используя формулу косинуса, разности, перепишем интегральную формулу Фурье в следующем виде: Пусть f(x) — четная функция. Тогда так что изравснства (5) имеем В случае нечетной f(x) аналогично получаем Если f(x) задана лишь на (0, -foo), то формула (6) продолжает f(x) на всю ось Ох четным образом, а формула (7) — нечетным. (7) Определение.
Функция называется косинус-преобразованием Фурье функции f(x). Из (6) следует, что для четной функции f(x) Это означает, что f(x), в свою очередь, является косинус-преобразованием для Fc(£). Иными словами, функции / и Fc являются взаимными косинус-преобразованиями. Определение. Функция называется синус-преобразованием Фурье функции f(x). Из (7) получаем, что для нечетной функции f(x) т.е. f и Fs являются взаимными синус-преобразованиями.
Пример 3 прамоугольный импульс:
Пусть f(t) — четная функция, определенная следующим образом: (рис. 3). Воспользуемся полученным результатом для вычисления интеграла В силу формулы (9) имеем Рис.3 0 0 В точке t = 0 функция f(t) непрерывна и равна единице. Поэтому из (12′) получим 2.2. Амплитудный и фазовый спектры интеграла Фурье Пусть периодическая с периодом 2т функция /(х) разлагается в ряд Фурье Это равенство можно записать в виде где — амплитуда колебания с частотой п, — фаза. На этом пути мы приходим к понятиям амплитудного и фазового спектров периодической функции.
Пример 4:
Найти амплитудный и фазовый спектры функции 4 Находим спектральную функцию Отсюда Графики этих функций изображены на рис. 4. §3. Свойства преобразования Фурье 1. Линейность. Если и G(0 — преобразования Фурье функций /(х) и д(х) соответственно, то при любых постоянных а и р преобразованием Фурье функции a f<x) + р д(х) будет функция a Пользуясь свойством линейности интеграла, имеем Таким образом, преобразование Фурье есть линейный оператор. Обозначая его через будем писать
| Если F(£) есть преобразование Фурье абсолютно |
интегрируемой на всей числовой оси функции /(ж), то F(() ограничена при всех . Пусть функция f(x) абсолютно интегрируема на всей оси — преобразование Фурье функции f(x). Тогда 3«fltsJ. Пусть f(x) — функция, допуска кнцэя преобразование Фурье, Л — дойств ительяов число. Фуниция fh(x) = f <z-h) называется сдвигом фунждии fh — действительное число. Показать, что 3. Преобразование Фурье и ооерэции дифференцирования.
Пусть абсолютно интегрируемая функция f(x) имеет производную f'(x), также абсолютно интегрируемую на всей оси Ох, так что /(я) стремится к нулю при |ж| —» +оо. Считая f'(x) гладкой функцией, запишем Интегрируя по частям, будем иметь Внеинтегральноеслагаемое обращается в нуль (так как , и мы получаем Таким образом, дифференцированию функции /(х) отвечает умножение ее образа Фурье ^П/] на множитель.
Если функция f(x) имеет глад*«е абсолютно интефируемые производные до порядка m включительно и все они, как и сама функция f(x), стремятся к нулю при то, интегрируя по частям нужное число раз, получим Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину и тем самым упрощает задачуинтегрирования некоторых видов дифференциальных уравнений.
Так как преобразование Фурье абсолютно интегрируемой функции f^kx) есть ограниченная функция от (свойство 2), то из соотношения (2) получаем для следующую оценку: ПРЕОБРАЗОВАНИЕ ФУРЬЕ Интеграл Фурье Комплексная форма интеграла Преобразование Фурье Косинус и синус преобразования Амплитудный и фазовый спектры Свойства Приложения Из этой оценки следует: чем больше функция f(x) имеет абсолютно интегрируемых производных, тем быстрее ее преобразование Фурье стремится к нулю при .
Замечание. Условие является достаточно естественным, поскольку обычная 1еория интегралов Фурье имеет дело с процессами, которые в том или ином смысле имеют начало и коней, но не продолжаются неограниченно с примерно одинаковой интенсивностью. 4. Связь между скоростью убывания функции f(x) при |z| —» -f оо и гладкостью ее преобразования Фурм. Предположим, что не только /(х), но и ее произведение xf(x) является абсолютно интегрируемой функцйей на всей оси Ох. Тогда преобразование Фурье ) будет дифференцируемой функцией.
Действительно, формальное дифференцирование по параметру £ подынтегральной функции приводит к интегралу который является абсолютно и равномерно сходящимся относительно параметра Следовательно, дифференцирование возможно, и Таким образом, т. е. операция умножения f(x) на аргумент х переходит после преобразования Фурье в операцию t щ. Если вместе с функцией f(x) абсолютно интегрируемыми на всей оси Ох являются функции , то процесс дифференцирования можно продолжить.
Получим, что функция имеет производные до порядка m включительно, причем Таким образом, чем быстрее функция f(x) убывает при тем более гладкой получается функция Теорема 2 (о сверле). Пусть- преобразования Фурье функций /,(ж) и f2(x) соответственно. Тогда причем двойной интеграл в правой части сходится абсолютно. Положим — х. Тогда будем иметь или, меняя порядок интегрирования, Функция называется сверткой функций и обозначается символом Формула (1) может быть теперь записана так: Отсюда видно, что преобразование Фурье свертки функций f(x) и f2(x) равно умноженному на у/2ж произведению преобразований Фурье свертываемых функций, Замечание.
Нетрудно установить следующие свойства свертки: 1) линейность: 2) коммутативность: §4. Приложения преобразования Фурье 1. Пусть Р(^) — линейный дифференциальный оператор порядка m с постоянными коэффициентами, Используя формулу для преобразования Фурье производных функции у(х), находим ‘ Рассмотрим дифференциальное уравнение где Р — введенный выше дифференциальный оператор. Предположим, что искомое решение у(х) имеет преобразование Фурье у (О. а функция f(x) имеет преобразование /(£)•
Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси относительно откуда так что формально где символ обозначает обратное преобразование Фурье. Основное ограничение применимости этого метода связано со следующим фактом. Решение обыкновенного дифференциального уравнения с постоянными коэффициентами содержит функции вида еЛ*, eaz cos fix, еах sin рх. Они не являются абсолютно интегрируемыми на оси -оо
Это ограничение можно обойти, если ввести в рассмотрение так называемые обобщенные функции. Однако в ряде случаев преобразование Фурье все же применимо в своей классической форме. Пример. Найти решение а = а(х, t) уравнения (а = const), при начальных условиях Это — задача о свободных колебаниях бесконечной однородной струны, когда задано начальное отклонение
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Фурье-вычисления для сравнения изображений
Традиционная техника “начального уровня”, сравнения текущего изображения с эталоном основывается на рассмотрении изображений как двумерных функций яркости (дискретных двумерных матриц интенсивности). При этом измеряется либо расстояние между изображениями, либо мера их близости.
Как правило, для вычисления расстояний между изображениями используется формула, являющаяся суммой модулей или квадратов разностей интенсивности:
Если помимо простого сравнения двух изображений требуется решить задачу обнаружения позиции фрагмента одного изображения в другом, то классический метод “начального уровня”, заключающийся в переборе всех координат и вычисления расстояния по указанной формуле, как правило, терпит неудачу практического использования из-за требуемого большого количества вычислений.
Одним из методов, позволяющих значительно сократить количество вычислений, является применение Фурье преобразований и дискретных Фурье преобразований для расчёта меры совпадения двух изображений при различных смещениях их между собой. Вычисления при этом происходят одновременно для различных комбинаций сдвигов изображений относительно друг друга.
Наличие большого числа библиотек, реализующих Фурье преобразований (во всевозможных вариантах быстрых версий), делает реализацию алгоритмов сравнения изображений не очень сложной задачей для программирования.
Видео:Решение дифференциальных уравнений с помощью степенных рядов -1Скачать

Постановка задачи
- Пусть даны два изображения X и Y – изображение и образец, размеров (N1,N2) и (M1,M2) соответственно и Ni > Mi
- Требуется найти координаты образца Y в полном изображении X и вычислить оценочную величину — меру близости.
Например, найти:
образец
в изображении
Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Корреляция как мера между изображениями
m(X,Y) = SUM ( X[i,j] * Y[i,j] ) / ( SQRT ( SUM X[i,j] ^2 ) * SQRT ( SUM Y[i,j] ^2 ) )
Данная величина получена из операции скалярного произведения векторов (рассматривая изображения как векторы в многомерном пространстве). И даже более — эта же формула представляет собой и стандартную статистическую формулу критерия для гипотезы о совпадении двух вероятностных распределений.
Примечание:
При вычислении корреляции между фрагментами изображений, если одно изображение меньше другого, будем делить только на значение норм у пересекающийся частей.
Видео:Преобразования #7: амплитудный и фазовый спектры преобразования ФурьеСкачать

Свёртка двух функций
Пусть G’(t) = G(-t) и F’(t) = F(-t), тогда, очевидна справедливость равенств:
- FхF’(0) = SUM F(i)^2 – скалярное произведение вектора F на самого себя
- GхG’(0) = SUM G(j)^2– скалярное произведение вектора G на самого себя
- FхG’(0) = SUM F(i)*G(i) – скалярное произведение двух векторов F и G
Так же очевидно, что FхG’(t) равна корреляции получаемой в результате сдвига одного вектора, относительно другого на шаг t (это легко проверить явной подстановкой значений в формулу корреляции).
Видео:Решить задачу Коши для дифференциального уравнения с помощью формулы ДюамеляСкачать

Преобразование Фурье
Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.
Преобразование Фурье функции f вещественной переменной является интегральным и задаётся следующей формулой:
Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.
Кроме того, существуют разнообразные обобщения данного понятия.
Видео:Операционное исчислениеСкачать

Многомерное преобразование Фурье
Преобразование Фурье функций, заданных на пространстве ℝ^n, определяется формулой:
Обратное преобразование в этом случае задается формулой:
Как и прежде, в разных источниках определения многомерного преобразования Фурье могут отличаться выбором константы перед интегралом.
Видео:ЗАЧЕМ в жизни нужно преобразование Фурье? В Первом Приближении. Чуть-Чуть о Науке #НаукаСкачать

Дискретное преобразование Фурье
Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать дифференциальные уравнения в частных производных и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.
Формулы дискретных преобразований
Дискретное преобразование Фурье является линейным преобразованием, которое переводит вектор временных отсчётов в вектор спектральных отсчётов той же длины. Таким образом преобразование может быть реализовано как умножение симметричной квадратной матрицы на вектор:
Фурье-преобразования для вычисления свёртки
Одним из замечательных свойств преобразований Фурье является возможность быстрого вычисления корреляции двух функций определённых, либо на действительном аргументе (при использовании классической формулы), либо на конечном кольце (при использовании дискретных преобразований).
И хотя подобные свойства присущи многим линейным преобразованиям, для практического применения, для вычисления операции свёртки, согласно данному нами определению, используется формула
Где
- FFT – операция прямого преобразования Фурье
- BFT – операция обратного преобразования Фурье
Проверить правильность равенства довольно легко – явно подставив в формулы Фурье-преобразований и сократив получившиеся формулы
Фурье-преобразования для вычисления корреляции
Пусть (t) равна корреляции получаемой в результате сдвига одного вектора, относительно другого на шаг t
Тогда, как уже показано ранее, выполняется
Фурье-преобразования для решения задачи
Упрощение формул для решения поставленной задачи
получаем, что
- = BFT ( FFT(X) * CONJUGATE ( FFT(Y) ) )
- = BFT ( SQUAREMAGNITUDE( FFT(X) ) * CONJUGATE ( FFT(E) ) )
Где
- (i,j) – скалярное произведение двух изображений, получаемых при сдвиге (i,j) относительно друг друга изображений X и Y
- E – изображение размера равному минимальным размерам X и Y, и заполненное единичными значениями (то есть “кадр” в котором сравниваются X и Y)
- (i,j) – норма (сумма яркостей пикселей) общей части изображения X при сдвиге (i,j)
- FFT – операция прямого двухмерного дискретного преобразования Фурье
- BFT – операция обратного двухмерного дискретного преобразования Фурье
- CONJUGATE – операция вычисления матрицы из сопряжённых элементов
- SQUAREMAGNITUDE– операция вычисления матрицы квадратов амплитуд элементов
Алгоритм поиска фрагмента в полном изображении
- Пусть даны два изображения X и Y – изображение и образец, размеров (N1,N2) и (M1,M2) соответственно и Ni > Mi
- Требуется найти координаты образца Y в полном изображении X и вычислить оценочную величину — меру близости.
- Расширить изображение Y до размера (N1,N2), дополнив его нулями
- Сформировать изображение E из единиц размера (M1,M2) и расширить до размера (N1,N2), дополнив его нулями
- Вычислить = BFT ( FFT(X) * CONJUGATE ( FFT(Y) ) )
- Вычислить = BFT ( SQUAREMAGNITUDE( FFT(X) ) * CONJUGATE ( FFT(E) ) )
- Вычислить M[i,j] = (f + [i,j])/(f + [i,j])
- В матрице M найти элемент с максимальным значением – координаты этого элемента и являются искомой позицией образца в полном изображении, а значение равно оценке меры сравнения.
Примечание:
При использовании дискретного преобразования Фурье, матрица M содержит также элементы от циклического сдвига изображений между собой. Поэтому, если не требуется анализировать циклический сдвиг кадров, то поиск максимального элемента в матрице M нужно ограничить областью (0,0)-(N1-M1, N2-M2).
Примеры реализации
Реализованные алгоритмы являются частью библиотеки с открытым исходным кодом FFTTools. Интернет-адрес: github.com/dprotopopov/FFTTools
Используемое программное обеспечение
- Microsoft Visual Studio 2013 C# — среда и язык программирования
- EmguCV/OpenCV – C++ библиотека структур и алгоритмов для обработки изображений
- FFTWSharp/FFTW – C++ библиотека реализующая алгоритмы быстрого дискретного преобразования Фурье