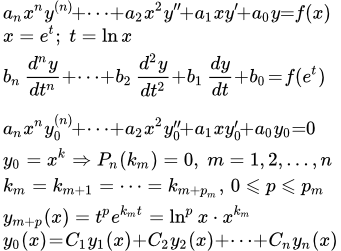Решение дифференциальных уравнений при помощи метода эйлера

Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.

Видео:Численное решение задачи Коши методом ЭйлераСкачать

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.

Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;

;
;
.

Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Решение однородного уравнения Эйлера

Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.

Рассмотрим действительные корни. Пусть k_i – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.

Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть k_i – кратный корень кратности m . Выразим комплексный корень k_i через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.

После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .

Примеры

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Решение неоднородного уравнения Эйлера

Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.

Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).

Пример

Видео:Дифференциальное уравнение. Формула ЭйлераСкачать

Неоднородное уравнение Эйлера со специальной неоднородной частью

Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.

Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.

Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020

Видео:Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

Метод Эйлера: для чего он нужен, порядок действий и упражнения

Метод Эйлера: для чего он нужен, порядок действий и упражнения — Наука

Видео:Метод ЭйлераСкачать

Содержание:

В Метод Эйлера Это самая базовая и простая из процедур, используемых для нахождения приближенных численных решений обыкновенного дифференциального уравнения первого порядка, при условии, что известно его начальное условие.

Обыкновенное дифференциальное уравнение (ОДУ) — это уравнение, которое связывает неизвестную функцию одной независимой переменной с ее производными.

Если наибольшая производная, которая появляется в уравнении, имеет степень один, то это обыкновенное дифференциальное уравнение первой степени.

Самый общий способ написать уравнение первой степени:

Видео:МЗЭ 2022 Численное решение дифференциальных уравнений Метод Эйлера Ложкин С. А.Скачать

Что такое метод Эйлера?

Идея метода Эйлера заключается в нахождении численного решения дифференциального уравнения в интервале между X₀ и X_F .

Сначала интервал дискретизируется на n + 1 балл:

Которые получаются так:
Икс_я= х₀+ я

Где h — ширина или шаг подынтервалов:

С начальным условием также можно узнать производную в начале:

Эта производная представляет собой наклон касательной к кривой функции y (x) точно в точке:

Затем делается приблизительный прогноз значения функции y (x) в следующей точке:

Затем была получена следующая приближенная точка решения, которая будет соответствовать:

Процедура повторяется для получения последовательных баллов.

На рисунке, показанном в начале, синяя кривая представляет точное решение дифференциального уравнения, а красная — последовательные приближенные точки, полученные с помощью процедуры Эйлера.

Видео:МЗЭ 2022 Численное решение дифференциальных уравнений. Неявный метод Эйлера. Ложкин С.А.Скачать

Решенные упражнения

Видео:Метод Эйлера. Решение систем ДУСкачать

Упражнение 1

я) Пусть дифференциальное уравнение имеет вид:

При начальном условии x = a = 0; Y_к= 1

Используя метод Эйлера, получить приближенное решение Y в координате X = b = 0,5, разбивая интервал [a, b] на n = 5 частей.

Видео:Видеоурок "Системы диф. уравнений. Метод Эйлера"Скачать

Решение

Численные результаты резюмируются следующим образом:

Из чего делается вывод, что решение Y для значения 0,5 составляет 1,4851.

Примечание: для проведения расчетов, Smath studio, бесплатная программа для бесплатного использования.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Упражнение 2.

II) Продолжая работу с дифференциальным уравнением из упражнения I), найдите точное решение и сравните его с результатом, полученным методом Эйлера. Найдите ошибку или разницу между точным и приблизительным результатом.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Решение

Точное решение найти не очень сложно. Производная функции sin (x) известна как функция cos (x). Следовательно, решение y (x) будет:

Для выполнения начального условия и (0) = 1 константа C должна быть равна 1. Затем точный результат сравнивается с приблизительным:

Сделан вывод, что в расчетном интервале аппроксимация имеет три значащих цифры точности.

Видео:Пример решения задачи Коши методом Эйлера. Метод Эйлера с пересчетом.Скачать

Упражнение 3.

III) Рассмотрим дифференциальное уравнение и его начальные условия, указанные ниже:

При начальном условии x₀ = 0; Y₀ = 1

Используйте метод Эйлера, чтобы найти приблизительные значения решения у (х) в интервале х = [0, 1,5]. Используйте шаг h = 0,1.

Видео:Численное решение обыкновенных дифференциальных уравнений в ExcelСкачать

Решение

Метод Эйлера очень подходит для использования с электронной таблицей. В этом случае мы будем использовать электронную таблицу геогебра бесплатная и бесплатная программа.

В электронной таблице на рисунке показаны три столбца (A, B, C), первый — это переменная Икс , второй столбец представляет переменную Y, а третий столбец — производная Y ‘.

Строка 2 содержит начальные значения Икс, Y, Y ‘ .

Шаг значения 0,1 помещен в ячейку абсолютного положения ($ D $ 4).

Начальное значение y0 находится в ячейке B2, а y1 — в ячейке B3. Чтобы вычислить y₁ используется формула:

Эта формула электронной таблицы будет иметь вид B3: = B2 + $ D $ 4 * C3.

Точно так же y2 будет в ячейке B4, и его формула показана на следующем рисунке:

На рисунке также показан график точного решения и точки A, B,…, P приближенного решения по методу Эйлера.

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Ньютоновская динамика и метод Эйлера

Классическая динамика была разработана Исааком Ньютоном (1643 — 1727). Первоначальная мотивация Леонарда Эйлера (1707 — 1783) к разработке своего метода заключалась именно в решении уравнения второго закона Ньютона в различных физических ситуациях.

Второй закон Ньютона обычно выражается в виде дифференциального уравнения второй степени:

куда Икс представляет положение объекта в момент т. Указанный объект имеет массу м и подвергается силе F. Функция F связана с силой и массой следующим образом:

Для применения метода Эйлера требуются начальные значения времени. т, скорость v и положение Икс.

В следующей таблице объясняется, как, начиная с начальных значений t1, v1, x1, можно получить приближение скорости v2 и положения x2 в момент t2 = t1 + Δt, где Δt представляет небольшое увеличение и соответствует шагу в методе Эйлер.

Видео:Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

Упражнение 4.

IV) Одна из фундаментальных проблем механики — это проблема блока массы M, привязанного к пружине (или пружине) с постоянной упругостью K.

Второй закон Ньютона для этой проблемы будет выглядеть так:

В этом примере для простоты мы возьмем M = 1 и K = 1. Найдите приблизительные решения для положения Икс и скорость v методом Эйлера на временном интервале [0, π / 2], разбивая интервал на 12 частей.

Возьмите 0 в качестве начального момента, начальную скорость 0 и начальное положение 1.

Видео:Численные методы решения ДУ: метод ЭйлераСкачать

Решение

Численные результаты представлены в следующей таблице:

Также отображаются графики положения и скорости между временами от 0 до 1,44.

Видео:дифференциальное уравнение ЭйлераСкачать

Предлагаемые упражнения для дома

Упражнение 1

Используйте электронную таблицу, чтобы найти приближенное решение с помощью метода Эйлера для дифференциального уравнения:

y ’= — Exp (-y) с начальными условиями x = 0, y = -1 в интервале x = [0, 1]

Начните с шага 0,1. Постройте результат.

Упражнение 2.

Используя электронную таблицу, найдите численные решения следующего квадратного уравнения, где y является функцией независимой переменной t.

y ’’ = -1 / y² с начальным условием t = 0; и (0) = 0,5; у ‘(0) = 0

Найдите решение на интервале [0,5; 1.0] с шагом 0,05.

Постройте результат: y vs t; y ‘vs t

Ссылки

1. Метод Эрлера Взято с wikipedia.org
2. Решатель Эйлера. Взято с en.smath.com

Американский флаг: история и значение

25 песен о любви, которые заставят вас плакать

Курсовая работа: Решение дифференциальных уравнений по методу Эйлера

Министерство образования Республики Беларусь

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра вычислительной математики и программирования

к курсовому проекту

« Решение дифференциальных уравнений по методу Эйлера »

2. Математическое объяснение метода

2.1 Метод Эйлера

2.2 Исправленный метод Эйлера

2.3 Модифицированный метод Эйлера

3. Блок-схема алгоритма программы

4. Описание программы

Список использованной литературы

Приложение 1 (Текст программы)

Приложение 2 (Результаты работы программы)

Уравнение, содержащие производную функции одной переменной, возникают во многих областях прикладной математики. Вообще говоря, любая физическая ситуация, где рассматривается степень изменения одной переменной по отношению к другой переменной, описывается дифференциальным уравнением, а такие ситуации встречаются довольно часто.

Решение обыкновенных дифференциальных уравнений (нелинейных) первого порядка с начальными данными (задача Коши) – классическая область применения численных методов. Имеется много разностных методов, часть из которых возникла в домашинную эпоху и оказалось пригодным для современных ЭВМ.

В этой программе использовался метод Эйлера, один из самых старых и широко известных методов численного интегрирования дифференциальных уравнений. Этот метод имеет довольно большую ошибку; кроме того, он очень часто оказывается неустойчивым – малая начальная ошибка быстро увеличивается с ростом Х. Поэтому чаще используют более точные методы, такие как: исправленный метод Эйлера и модифицированный метод Эйлера. Нужно, однако, заметить, что метод Эйлера является методом Рунге – Кутта первого порядка.

2. Математическое объяснение метода

2.1 Метод Эйлера

Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х₀ , х₁ …, х_n и числа у₀ , не определяя функцию у=F(x), найти такие значения у₁ , у₂ ,…, у_n , что у_i =F(x_i )(i=1,2,…, n) и F(x₀ )=y₀ .

Таким образом, численные методы позволяют вместо нахождения функции

У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k -x_k-1 называется шагом интегрирования.

Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Рассмотрим дифференциальное уравнение первого порядка

с начальным условием

Требуется найти решение уравнения (1) на отрезке [а,b].

Разобьем отрезок [a, b] на n равных частей и получим последовательность х₀ , х₁ , х₂ ,…, х_n , где x_i =x₀ +ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.

В методе Эйлера приближенные значения у(х_i )»y_i вычисляются последовательно по формулам у_i +hf(x_i , y_i ) (i=0,1,2…).

При этом искомая интегральная кривая у=у(х), проходящая через точку М₀ (х₀ , у₀ ), заменяется ломаной М₀ М₁ М₂ … с вершинами М_i (x_i , y_i ) (i=0,1,2,…); каждое звено М_i M_i+1 этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (1), которая проходит через точку М_i , смотри рисунок 1.

Если правая часть уравнения (1) в некотором прямоугольнике R<|x-x₀ |£a, |y-y₀ |£b>удовлетворяет условиям:

|df/dx|=|df/dx+f(df/dy)| £ M (M=const),

то имеет место следующая оценка погрешности:

где у(х_n )-значение точного решения уравнения(1) при х=х_n , а у_n — приближенное значение, полученное на n-ом шаге.

Формула (3) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет : сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагомh/2. Погрешность более точного значения у_n * оценивается формулой

Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.

2.2 Исправленный метод Эйлера

В исправленном методе Эйлера мы находим средний тангенс наклона касательнй для двух точек: x_m , y_m и x_m +h, y_m +hy’_m . Последняя точка есть та самая, которая в простом методе обозначалась x_m+1 , y_m+1 . Геометрический процесс нахождения точки x_m+1 , y_m+1 можно проследить по рисунку 2. С помощью метода Эйлера находится точка x_m +h, y_m +hy’_m, лежащая на прямой L_1. В этой точке снова вычисляется тангенс угла наклона касательной, на рисунке этому значению соответствует прямая L₂ . Усреднение двух тангенсов дает прямую L’₃ . Наконец, через точку x_m , y_m мы проводим прямую L₃ параллельную L’₃ . Точка, в которой прямая L₃ пересечется с ординатой, восстановленной из x= x_m+1 =x_m +h, и будет искомой точкой y= y_m+1 = y_m +hy’_m . Тангенс угла наклона L₃ равен:

Уравнение линии L₃ при этом записывается в виде:

Соотношения 5, 6, 7 и 8 описывают исправленный метод Эйлера. (рис. 2)

2.3 Модифицированный метод Эйлера

Этот метод более точен. Рассмотрим дифференциальное уравнение (1) с начальным условием y(x₀ )=y₀ . Разобьем наш участок интегрирования на n равных частей. На малом участке [x₀ ,x₀ +h] интегральную кривую заменимпрямой линией. Получаем точкуМ_к (х_к ,у_к ). (рис. 3)

N_k / _y=y(x)

М_к М_к /

Y_k+1

Y_k

х_к х_к1/2 x_k+h =x_k1 X

Получаем точку N_k / . В этой точке строим следующую касательную:

Из точки М_к проводим прямую с угловым коэффициентом α_к и определяем точку пересечения этой прямой с прямой x_к1 . Получаем точку М_к / . В качестве у_к+1 принимаем ординату точки М_к / . Тогда:

Эти формулы называются рекуррентными формулами метода Эйлера.

Сначала вычисляют вспомогательные значения искомой функции y_к+1/2 в точках x_к+1/2 , затем находят значение правой части уравнения (1) в средней точке

3. Блок-схема алгоритма

где A — начальное значение x, B — конечное значение x, F(x) — значение функции в точке x_n , N — количество промежутков, st – выбор операции, C1,C2,C3 – константы для формул, nom — сохраняет номер используемой функции.

На рисунке представлена блок-схема процесса решения дифференциального уравнения методом Эйлера

Подсчитывая каждый раз новое значение уравнения F(x), получаем последовательность значений x_n y_n , n=1,2,…

По этим значениям строим график.

4. Описание программы

Программа весьма проста. В ней много предусмотрено моментов неправильного ввода данных, о которых программа предупреждает пользователя и сразу же просит повторно ввести данные.

С самого начала программа предоставляет пользователю меню выполняемых функций, которые выделяются при помощи стрелок ↑ и ↓ выбор клавишей Enter:

После запуска программы нужно выбрать Formyla -> Enter, эта опция позволит из предложенного списка формул выбрать одну, по которой компьютер будет производить расчет и строить график. Все предложенные формулы имеют номерацию; чтобы выбрать интересующий вас пример нажмите на цифру равную номеру примера, и сразу же появится новое окно, в котором сверху будет записан ваш пример. Также в окне будет этот же пример но с нулями на месте констант. Под примером будет высвечена большая буква С, это используется для ввода констант. Для этого вам нужно нажать номер константы, он появится, и после знака равно запишите чему она равна (вводятся целые и вещественные значения). По окончании набора нажать Enter. Операцию повторять пока не будут введены все числа. По окончании нажать Esc. После появится строчка «уточните границы изменения Х, от A= до B= » здесь нужно занести данные на каком промежутке абсциссы будет рассматриваться функция. Следующая строчка попросит ввести начальные данные y(A)=. Следующей строчкой будет вопрос: «сохранить данные в файле? Да/Нет» ответить на этот вопрос с помощью клавиш Д и Н (рус), после чего программа вернется в первоначальное меню. Если данные были сохранены (в папке с программой появляется файл form.txt), то в следующий раз чтобы не набирать снова выберите в меню опцию Formyla -> Open in fails и на экране появятся введенные данные с пометкой снизу, сообщая что данные были прочитаны из файла.

Следующая опция Reshenie. После нажатия в окне просят ввести N(целое число) – число промежутков, на которые разделится рассматриваемый участок (ось ОХ). После появится таблица рассчитанных данных (номер точки, значение абсциссы, значение ординаты). При нажатии любой клавиши произойдет переход в меню.

Graphic эта опция позволяет визуально видеть решение, а так же на этом графике прописываются все данные: начальная формула, шаг и промежуток построения графика, масштаб, данные об его изменении(клавишами +(увеличить) и -(уменьшить), а также возможность определить точное значение функции в любой точке.

Опция Exit применяется для выхода из программы.

Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать дифференциальные уравнения по методу Эйлера, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности.

Данная программа решает заданную пользователем дифференциальное уравнение за минимальный промежуток времени. При этом пользователю предоставляется возможность визуально оценить решение, рассматривая график полученного решения.

К достоинствам программы можно отнести также удобный пользовательский интерфейс, возможность ввода пользовательских дифференциальных уравнений, а также давольно высокая стабильность работы. Однако имеются и некоторые недостатки. К недостаткам программы можно отнести: критичность к вводимым пользователем урававней, отсутствие обработки исключительных событий. Это, естественно, ограничивает возможности программы.

Список использованной литературы

1. Д. Мак-Кракен, У. Дорн. Численные методы и программирование на фортране. –М.: Мир,1977.-389,396-408 с.

2. А.А. Самарский. Введение в численные методы. – М.:Наука,1987.-176 с.

3. Алгоритмы вычислительной математики: Лабораторный практикум по курсу «Программирование» для студентов 1 — 2-го курсов всех специальностей БГУИР/А.К. Синицын, А.А. Навроцкий.- Мн.: БГУИР, 2002.- 65-69 с.

4. ГОСТ 2.105-95. Общие требования к текстовым документам.

5. ГОСТ 7.32-91. Система стандартов по информации, библиотечному и издательскому делу. Отчет о НИР. Структура и правила оформления.

Приложение 1. Текст программы.

void formyl(int p)

if(p==1) printf(«n 1. C1*y’ = C2*y + C3*x + C4*x*y»);

else if(p==2) printf(«n 2. y’/(C1-100) = C2*y + C3*x + (C4+x)*y»);

else if(p==3) printf(«n 3. pow(e,C1)*y’ = C2*y + C3*cos(x) + (C4+x+y)»);

else if(p==4) printf(«n 4. C1*sin(x)*y’ = e*C2*y + C3*arcsin(x) + C4*y/x»);

else if(p==5) printf(«n 5. C1*y’ = sin(C2)*y + tg(C3*x) + C4*ln(x)*y»);

else if(p==6) printf(«n 6. C1*y’ = y*C2 + C3*sin(x) + C4*cos(x)*y»);

else if(p==7) printf(«n 7. (C1+C2+C3+C4)*y’ = C2*y + (C3-x) + lg(C4*x)*y»);

else if(p==8) printf(«n 8. y’/C1 = y/C2 + C3*sin(x) + C4*x*y»);

else if(p==9) printf(«n 9. sin(C1)*y’ = C2*y + |C3|*x + x*y/C4»);

void formyl2(int p,double C1,double C2,double C3,double C4)

else if(p==2) printf(«y’/(%.2f-100)=%.2f*y+%.2f*x+(%.2f+x)*y»,C1,C2,C3,C4);else if(p==3) printf(«pow(e,%.2f)*y’=%.2f*y+%.2f*cos(x)+(%.2f+x+y)»,C1,C2,C3,C4);

else if(p==4) printf(«%.2f*sin(x)*y’=e*%.2f*y+%.2f*arcsin(x)+%.2f*y/x»,C1,C2,C3,C4);

else if(p==5) printf(«%.2f*y’=sin(%.2f)*y+tg(%.2f*x)+%.2f*ln(x)*y»,C1,C2,C3,C4);

else if(p==6) printf(«%.2f*y’=y*%.2f+%.2f*sin(x)+%.2f*cos(x)*y»,C1,C2,C3,C4);

else if(p==8) printf(«y’/%.2f=y/%.2f+%.2f*sin(x)+%.2f*x*y»,C1,C2,C3,C4);

else if(p==9) printf(«sin(%.2f)*y’=%.2f*y+|%.2f|*x+x*y/%.2f»,C1,C2,C3,C4);

double formyl3(int p,double h,double x,double y,double C1,double C2,double C3,double C4)

else if(p==2) Y=h*(C1-100)*(y*C2+C3*x+(C4+x)*y)+y;

else if(p==3) Y=h*(C2*y+C3*cos(x)+C4+x+y)/exp(C1)+y;

else if(p==4) Y=h*(exp(1)*C2*y+C3*asin(x)+C4*y/x)/(C1*sin(x))+y;

else if(p==5) Y=h*(sin(C2)*y+tan(C3*x)+C4*log10(x)*y)/C1+y;

else if(p==6) Y=h*(y*C2+C3*sin(x)+C4*cos(x)*y)/C1+y;

else if(p==7) Y=h*(C2*y+(C3-x)+log10(C4*x)*y)/(C1+C2+C3+C4)+y;

else if(p==8) Y=h*(y/C2+C3*sin(x)+C4*x*y)*C1+y;

else if(p==9) Y=h*(C2*y+abs(C3)*x+x*y/C4)/sin(C1)+y;

int vv=0,vv1=0; // руководит операциями

int N=0,W; // кол промежутков

int i,j,k; // используются во всех «for»

int nom; // номер примера

int st=4,vst=0; // строчка в меню

double C1,C2,C3,C4; // константы

double M; // масштаб

double xtoch,ytoch; // считает y(x) по графику

double A=0,B=0,ii,jj,kk; // пределы интегрирования

double x[102],y[102]; // главные переменные x,y

int g_driver=9,g_mode=2, g_error;

printf(«n error=%d, reason=%sn», g_error, grapherrormsg(g_error));