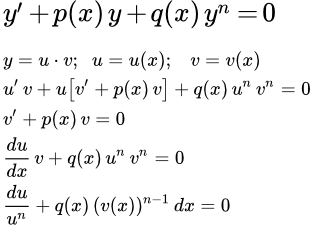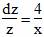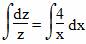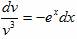Решение дифференциальных уравнений по методу бернулли

Видео:Уравнение Бернулли Метод БернуллиСкачать

Дифференциальное уравнение Бернулли и методы его решения

Видео:10. Уравнения БернуллиСкачать

Решение дифференциального уравнения Бернулли приведением к линейному уравнению

Рассмотрим дифференциальное уравнение Бернулли:
(1) ,
где n ≠ 0 , n ≠ 1 , p и q – функции от x .
Разделим его на y n . При y ≠ 0 или n 0 имеем:
(2) .
Это уравнение сводится к линейному с помощью замены переменной:
.
Покажем это. По правилу дифференцирования сложной функции:
;
.
Подставим в (2) и преобразуем:
;
.
Это – линейное, относительно z , дифференциальное уравнение. После его решения, при n > 0 , следует рассмотреть случай y = 0 . При n > 0 , y = 0 также является решением уравнения (1) и должно входить в ответ.

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Решение методом Бернулли

Рассматриваемое уравнение (1) также можно решить методом Бернулли. Для этого ищем решение исходного уравнения в виде произведения двух функций:
y = u·v ,
где u и v – функции от x . Дифференцируем по x :
y′ = u′ v + u v′ .
Подставляем в исходное уравнение (1):
;
(3) .
В качестве v возьмем любое, отличное от нуля, решение уравнения:
(4) .
Уравнение (4) – это уравнение с разделяющимися переменными. Решаем его и находим частное решение v = v ( x ) . Подставляем частное решение в (3). Поскольку оно удовлетворяет уравнению (4), то выражение в круглых скобках обращается в нуль. Получаем:
;
.
Здесь v – уже известная функция от x . Это уравнение с разделяющимися переменными. Находим его общее решение, а вместе с ним и решение исходного уравнения y = uv .

Видео:Линейные дифференциальные уравнения (Метод Бернулли)Скачать

Примеры решений дифференциального уравнения Бернулли

Пример 1

Решить уравнение
(П1.1)

Это дифференциальное уравнение Бернулли. Решаем его методом Бернулли. Ищем решение в виде произведения двух функций: . Тогда
. Подставляем в (П1.1):
;
(П1.2) .
Одну из этих функций мы можем выбрать произвольным образом. Выберем v так, чтобы выражение в круглых скобках равнялось нулю:
(П1.3) .
Тогда подставляя (П1.3) в (П1.2), мы получим дифференциальное уравнение с разделяющимися переменными:
(П1.4) .

Сначала мы определим функцию v . Нам нужно найти любое, отличное от нуля, решение уравнения (П1.3). Решаем его. Для этого разделяем переменные и интегрируем.
;
;
;
;
.
Отсюда , или . Возьмем решение с и знаком ′плюс′. Тогда , или .

Итак, мы нашли функции u и v . Находим искомую функцию y :
.
Заменим постоянную интегрирования: . Тогда общее решение исходного уравнения (П1.1) примет вид:
.

Когда мы делили на u , то предполагали, что . Теперь рассмотрим случай . Тогда . Нетрудно видеть, что постоянная функция также является решением исходного уравнения (П1.1) ⇑.

Общее решение уравнения: .
Уравнение также имеет решение .

Пример 2

На первый взгляд, кажется, что это дифференциальное уравнение не похоже на уравнение Бернулли. Если считать x независимой переменной, а y – зависимой (то есть если y – это функция от x ), то это так. Но если считать y независимой переменной, а x – зависимой, то легко увидеть, что это – уравнение Бернулли.

Итак, считаем что x является функцией от y . Подставим в исходное уравнение и умножим на :
;
;
(П2.1) .
Это – уравнение Бернулли с n = 2 . Оно отличается от рассмотренного выше, уравнения (1), только обозначением переменных ( x вместо y ). Решаем методом Бернулли. Делаем подстановку:
x = u v ,
где u и v – функции от y . Дифференцируем по y :
.
Подставим в (П2.1):
;
(П2.2) .
Ищем любую, отличную от нуля функцию v ( y ) , удовлетворяющую уравнению:
(П2.3) .
Разделяем переменные и интегрируем:
;
;
.
Поскольку нам нужно любое решение уравнения (П2.3), то положим C = 0 :
; ; .
Возьмем решение со знаком ′плюс′:
.
Подставим в (П2.2) учитывая, что выражение в скобках равно нулю (ввиду (П2.3)):
;
;
.
Разделяем переменные и интегрируем. При u ≠ 0 имеем:
;
(П2.4) ;
.
Во втором интеграле делаем подстановку :
;
.
Интегрируем по частям:
;
.
Подставляем в (П2.4):
.
Возвращаемся к переменной x :
;
;
.

Автор: Олег Одинцов . Опубликовано: 07-08-2012 Изменено: 29-10-2020

Видео:Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

Уравнения Бернулли

Назначение сервиса . Онлайн калькулятор можно использовать для проверки решения дифференциальных уравнений Бернулли.

• Решение онлайн
• Видеоинструкция

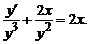
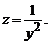
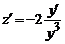
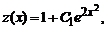
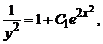
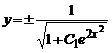
Пример 1 . Найти общее решение уравнения y’ + 2xy = 2xy 3 . Это уравнение Бернулли при n=3. Разделив обе части уравнения на y 3 получаем Делаем замену Тогда и поэтому уравнение переписывается в виде -z’ + 4xz = 4x. Решая это уравнение методом вариации произвольной постоянной, получаем откуда или, что то же самое, .

Пример 2 . y’+y+y 2 =0
y’+y = -y 2

Разделим на y 2
y’/y 2 + 1/y = -1

Делаем замену:
z=1/y n-1 , т.е. z = 1/y 2-1 = 1/y
z = 1/y
z’= -y’/y 2

Получаем: -z’ + z = -1 или z’ — z = 1

Далее надо найти z и выразить через него y = 1/z .

Пример 3 . xy’+2y+x 5 y 3 e x =0
Решение.
а) Решение через уравнение Бернулли.
Представим в виде: xy’+2y=-x 5 y 3 e x . Это уравнение Бернулли при n=3 . Разделив обе части уравнения на y 3 получаем: xy’/y 3 +2/y 2 =-x 5 e x . Делаем замену: z=1/y 2 . Тогда z’=-2/y 3 и поэтому уравнение переписывается в виде: -xz’/2+2z=-x 5 e x . Это неоднородное уравнение. Рассмотрим соответствующее однородное уравнение: -xz’/2+2z=0
1. Решая его, получаем: z’=4z/x

Интегрируя, получаем:
ln(z) = 4ln(z)
z=x 4 . Ищем теперь решение исходного уравнения в виде: y(x) = C(x)x 4 , y'(x) = C(x)’x 4 + C(x)(x 4 )’
-x/2(4C(x) x 3 +C(x)’ x 4 )+2y=-x 5 e x
-C(x)’ x 5 /2 = -x 5 e x или C(x)’ = 2e x . Интегрируя, получаем: C(x) = ∫2e x dx = 2e x +C
Из условия y(x)=C(x)y, получаем: y(x) = C(x)y = x 4 (C+2e x ) или y = Cx 4 +2x 4 e x . Поскольку z=1/y 2 , то получим: 1/y 2 = Cx 4 +2x 4 e x

б) решение через замену переменных
y=uv
x(u’v + uv’)+2uv+x 5 u 3 v 3 e x =0
v(x u’ + 2u) + xuv’+ x 5 u 3 v 3 e x = 0
a) xu’+2u = 0
или ln(u)=ln(x -2 ). Откуда u = x -2
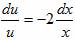
b) xuv’+ x 5 u 3 v 3 e x = 0
x x -2 v’+ x 5 x -6 v 3 e x = 0
v’/x+ v 3 e x /x = 0
v’+ v 3 e x = 0

или 1/y 2 = Cx 4 +2x 4 e x

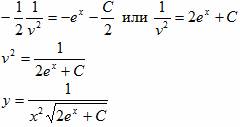
Видео:Дифференциальные уравнения Бернулли| poporyadku.schoolСкачать

Дифференциальное уравнение Бернулли

Статья раскрывает методы решения дифференциального уравнения Бернулли. В заключении будут рассмотрены решения примеров с подробным объяснением.

Видео:#Дифуры I. Урок 5. Линейные дифференциальные уравнения. Метод БернуллиСкачать

Приведение к линейному уравнению 1 порядка

Дифференциальное уравнение Бернулли записывается как y ‘ + P ( x ) · y = Q ( x ) · y n . Если n = 1 , тогда его называют с разделяющими переменными. Тогда уравнение запишется как y ‘ + P ( x ) · y = Q ( x ) · y ⇔ y ‘ = Q ( x ) — P ( x ) · y .

Для того, чтобы решить такое уравнение, необходимо первоначально привести к линейному неоднородному дифференциальному уравнению 1 порядка с новой переменной вида z = y 1 — n . Проделав замену, получаем, что y = z 1 1 — n ⇒ y ‘ = 1 1 — n · z n 1 — n · z ‘ .

Отсюда вид уравнения Бернулли меняется:

y ‘ + P ( x ) · y = Q ( x ) · y n 1 1 — n · z 1 1 — n · z ‘ + P ( x ) · z 1 1 — n = Q ( x ) · z 1 1 — n z ‘ + ( 1 — n ) · P ( x ) · z = ( 1 — n ) · Q ( x )

Этот процесс вычисления и подстановки способствует приведению к линейному неоднородному дифференциальному уравнению первого порядка. В итоге проводим замену и получаем его решение.

Найти общее решение для уравнения вида y ‘ + x y = ( 1 + x ) · e — x · y 2 .

Решение

По условию имеем, что n = 2 , P ( x ) = x , Q ( x ) = ( 1 + x ) · e — x . Необходимо ввести новую переменную z = y 1 — n = y 1 — 2 = 1 y , отсюда получим, что y = 1 z ⇒ y ‘ = — z ‘ z 2 . Провести замену переменных и получить ЛНДУ первого порядка. Запишем, как

y ‘ + x y = ( 1 + x ) · e — x · y 2 — z ‘ z 2 + x z = ( 1 + x ) · e — x · 1 z 2 z ‘ — x z = — ( 1 + x ) · e — x

Следует проводить решение при помощи метода вариации произвольной постоянной.

Проводим нахождение общего решения дифференциального уравнения вида:

d z d x — x z = 0 ⇔ d z z = x d x , z ≠ 0 ∫ d z z = ∫ x d x ln z + C 1 = x 2 2 + C 2 e ln z + C 1 = e x 2 2 + C 2 z = C · e x 2 2 , C = e C 2 — C 1

Где z = 0 , тогда решение дифференциального уравнения считается z ‘ — x z = 0 , потому как тождество становится равным нулю при нулевой функции z . Данный случай записывается как z = C ( x ) · e x 2 2 , где С = 0 . Отсюда имеем, что общим решением дифференциального уравнения z ‘ — x z = 0 считается выражение z = C · e x 2 2 при С являющейся произвольной постоянной.

Необходимо варьировать переменную для того, чтобы можно было принять
z = C ( x ) · e x 2 2 как общее решение дифференциального уравнения вида z ‘ — x z = — ( 1 + x ) · e — x .

Отсюда следует, что производится подстановка вида

C ( x ) · e x 2 2 ‘ — x · C ( x ) · e x 2 2 = — ( 1 + x ) · e — x C ‘ ( x ) · e x 2 2 + C ( x ) · e x 2 2 ‘ — x · C ( x ) · e x 2 2 = — 1 + x · e — x C ‘ ( x ) · e x 2 2 + C ( x ) · x · e x 2 2 — x · C ( x ) · e x 2 2 = — ( 1 + x ) · e — x C ‘ ( x ) · e x 2 2 = — ( 1 + x ) · e — x 2 2 — x C ( x ) = ∫ — ( 1 + x ) · e — x 2 2 — x d x = ∫ e — x 2 2 — x d — x 2 2 — x = e — x 2 x — x + C 3

С 3 принимает значение произвольной постоянной. Следовательно:

z = C x · e x 2 2 = e — x 2 2 — x + C 3 · e x 2 2 = e — x + C 3 · e x 2 2

Дальше производится обратная замена. Следует, что z = 1 y считается за y = 1 z = 1 e — x + C 3 · e x 2 2 .

Ответ: это решение считается решением исходного дифференциального уравнения Бернулли.

Видео:Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

Представление произведением функций u ( x ) и v ( x )

Имеется другой метод решения дифференциального уравнения Бернулли, который основывается на том, что функцию представляют при помощи произведения функций u ( x ) и v ( x ) .

Тогда получаем, что y ‘ = ( u · v ) ‘ = u ‘ · v + u · v ‘ . Производим подстановку в уравнение Бернулли y ‘ + P ( x ) · y = Q ( x ) · y n и упростим выражение:

u ‘ · v + u · v ‘ + P ( x ) · u · v = Q ( x ) · u · v n u ‘ · v + u · ( v ‘ + P ( x ) · v ) = Q ( x ) · u · v n

Когда в качестве функции берут ненулевое частное решение дифференциального уравнения v ‘ + P ( x ) · v = 0 , тогда придем к равенству такого вида

u ‘ · v + u · ( v ‘ + P ( x ) · v ) = Q ( x ) · ( u · v ) n ⇔ u ‘ · v = Q ( x ) · ( u · v ) n .

Отсюда следует определить функцию u .

Решить задачу Коши 1 + x 2 · y ‘ + y = y 2 · a r c t g x , y ( 0 ) = 1 .

Решение

Переходим к нахождению дифференциального уравнения вида 1 + x 2 · y ‘ = y · a r c t g x , которое удовлетворяет условию y ( 0 ) = 1 .

Обе части неравенства необходимо поделить на x 2 + 1 , после чего получим дифференциальное уравнение Бернулли y ‘ + y x 2 + 1 = y 2 · a r c t g x x 2 + 1 .

Перейдем к поиску общего решения.

Принимаем y = u · v , отсюда получаем, что y ‘ = u · v ‘ = u ‘ · v + u · v ‘ и уравнение запишем в виде

y ‘ + y x 2 + 1 = y 2 · a r c t g x x 2 + 1 u ‘ · v + u · v ‘ + u · v x 2 + 1 = u · v 2 · a r c t g x x 2 + 1 u ‘ · v + u · v ‘ + v x 2 + 1 = u 2 · v 2 · a r c t g x x 2 + 1

Проведем поиск частного решения с наличием разделяющих переменных v ‘ + v x 2 + 1 = 0 , отличных от нуля. Получим, что

d v v = — d x x 2 + 1 , v ≠ 0 ∫ d v v = — ∫ d x x 2 + 1 ln v + C 1 = — a r c t g x + C 2 v = C · e — a r c t g x , C = e C 2 — C 1

В качестве частного решения необходимо брать выражение вида v = e — a r c r g x . Преобразуем и получим, что

u ‘ · v + u · v ‘ + v x 2 + 1 = u 2 · v 2 · a r c r g x x 2 + 1 u ‘ · v + u · 0 = u 2 · v 2 · a r c t g x x 2 + 1 u ‘ = u 2 · v · a r c t g x x 2 + 1 u ‘ = u 2 · e — a r c t g x · a r c t g x x 2 + 1 ⇔ d u u 2 = e — a r c t g x · a r c t g x x 2 + 1 d x , u ≠ 0 ∫ d u u 2 = ∫ e — a r c t g x · a r c t g x x 2 + 1 d x ∫ d u u 2 = ∫ e — a r c t g x · a r c t g x d ( a r c t g x )

Имеем, что u = 0 рассматривается как решение дифференциального уравнения. Далее необходимо решить каждый из полученных интегралов по отдельности.

Интеграл с левой стороны, имеющего вид ∫ d u u 2 , необходимо найти по таблице первообразных. Получаем, что

∫ d u u 2 = — 1 u + C 3 .

Чтобы найти интеграл вида ∫ e — a r c t g x · a r c t g x d ( a r c t g x ) , принимаем значение a r c t g x = z и применяем метод интегрирования по частям. Тогда имеем, что

∫ e — a r c t g x · a r c t g x d ( a r c t g x ) = a r c t g x = z = = ∫ e — z · z d z = u 1 = z , d v 1 = e — z d z d u 1 = d z , v 1 = — e — z = = — z · e — z + ∫ e — z d z = — z · e — z — e — z + C 4 = = — e — z · ( z + 1 ) + C 4 = — e — a r c t g x · ( a r c t g x + 1 ) + C 4

— 1 u + C 3 = — e — a r c t g x · a r c t g x + 1 + C 4 1 u = e — a r c r g x · a r c t g x + 1 + C 3 — C 4 u = 1 e — a r c r g x · ( a r c t g x + 1 ) + C

Отсюда находим, что

y = u · v = e — a r c t g x e — a r c r g x · ( a r c t g x + 1 ) + C и y = 0 · v = 0 · e — a r c r g x = 0 являются решениями дифференциального уравнения Бернулли вида y ‘ + y x 2 + 1 = y 2 · a r c t g x x 2 + 1 .

На данном этапе следует переходить к поиску частного решения, которое удовлетворяет начальному условию. Получим, что

y = e — a r c t g x e — a r c t g x · a r c t g x + 1 + C , тогда запись примет вид y 0 = e — a r c t g 0 e — a r c t g 0 · a r c t g 0 + 1 + C = 1 1 + C .

Очевидно, что 1 1 + C = 1 ⇔ C = 0 . Тогда искомой задачей Коши будет являться полученное уравнение вида y = e — a r c t g x e — a r c t g x · a r c t g x + 1 + 0 = 1 a r c t g x + 1 .

💡 Видео

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Метод БернуллиСкачать

9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Уравнения Бернулли. Дифференциальны уравненияСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Линейное дифференциальное уравнение. Метод БернуллиСкачать

Линейные дифференциальные уравнения 1 порядка. Уравнения БернуллиСкачать

Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать

ВМ. 6.2 Дифференциальные уравнения. Метод БернуллиСкачать

Дифференциальные уравнения. Уравнение БернуллиСкачать

Метод Бернулли. Метод ЛагранжаСкачать