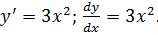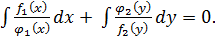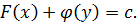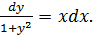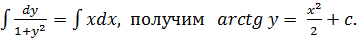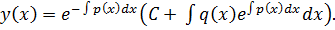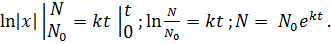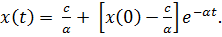Автор работы: Пользователь скрыл имя, 17 Сентября 2013 в 19:44, реферат
Краткое описание
Исследование многих физических и технических задач, а так же задач медицины, сводится к решению дифференциальных уравнений. С их помощью описывают волновые процессы и колебания, поэтому практическое применение дифференциальных уравнений очень разнообразно. В медицине дифференциальные уравнения используются, например: для определения скорости кровотока, скорости движения клапанов и стенок сердца (эхокардиография), определения вязкости крови и других параметров гемодинамики; для описания медико-биологических приложений ультразвука: эхоэнцефалограмма, УЗИ, ультразвуковая физиотерапия, ультразвуковая локация и кардиография; .
Прикрепленные файлы: 1 файл
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

реферат информатика.docx
Позволив говорить о половине собаки, мы допустили некоторую вольность, в дальнейшем мы усугубим эту вольность, используя такие понятия, как –3 кошки.
У. Сойер. Путь в современную математику
Исследование многих физических и технических задач, а так же задач медицины, сводится к решению дифференциальных уравнений. С их помощью описывают волновые процессы и колебания, поэтому практическое применение дифференциальных уравнений очень разнообразно.
В медицине дифференциальные уравнения используются, например:
- для определения скорости кровотока, скорости движения клапанов и стенок сердца (эхокардиография), определения вязкости крови и других параметров гемодинамики;
- для описания медико-биологических приложений ультразвука: эхоэнцефалограмма, УЗИ, ультразвуковая физиотерапия, ультразвуковая локация и кардиография;
- для описания процессов физиологической акустики, которая изучает устройство и работу звуковоспринимающих и звуковоспроизводящих органов человека и животных;
- для определения функции изменения численности популяции микроорганизмов в зависимости от времени.
Эти и другие области применения дифференциальных уравнений делают их одной из самых актуальных и важных разделов математики.
Первой содержательной математической моделью, описывающей биологические сообщества (если не считать исследований Фибоначчи популяции кроликов, приведших его к знаменитым числам, носящим его имя, а также исследований Мальтуса, приведших впоследствии к известному уравнению xy’ = ax (a > 0) мальтузианского роста) была модель Лотки — Вольтерры. Она описывает популяцию, состоящую из двух взаимодействующих видов. Первый из них, именуемый хищниками, при отсутствии второго вымирает по закону
а второй — жертвы — при отсутствии хищников неограниченно размножается в соответствии с законом Мальтуса. Взаимодействие двух этих видов моделируется так. Жертвы вымирают со скоростью, равной числу встреч хищников и жертв, которое в данной модели предполагается пропорциональным численности обеих популяций, т. е. равной dxy (d > 0). Поэтому
Хищники же размножаются со скоростью, пропорциональной числу съеденных жертв:
(c > 0). Система уравнений
описывающая такую популяцию хищник — жертва и называется системой (или моделью) Лотки — Вольтерры.
Таким образом, численности популяций хищников и жертв совершают рассогласованные по фазе автоколебания (см. рис.1). Такое поведение часто наблюдается в природе (классическая ссылка здесь на отчет Компании Гудзонова залива, которая в течение долгих лет наблюдала за численностью популяций зайцев и рысей в Канаде). Однако, система Лотки — Вольтерры обладает одним существенным недостатком: она неустойчива по отношению к малым возмущениям самой модели, точнее, не является грубой.
Поскольку в реальных популяциях присутствует много возмущающих факторов, не учтенных в модели Лотки — Вольтерры, эта модель вряд ли может претендовать на адекватное описание реальности. Этого недостатка лишена модель Холлинга — Тэннера, учитывающая большее число реальных факторов. В этой модели скорость изменения популяции хищников задается выражением ax – bx2/y = x(a – bx/y). Оно выбрано из следующих соображений. Когда пищи (жертв) много (y » +Ґ), популяция хищников растет по правилу Мальтуса с показателем a. С уменьшением числа жертв скорость роста популяции хищников падает и при y 0). Это выражение правдоподобнее описывает межвидовое взаимодействие, нежели соответствующий член –dxy модели Лотки — Вольтерры. В последней число жертв, убиваемых одним хищником за единицу времени, равно dy и растет пропорционально числу жертв, что неправдоподобно. В модели Холлинга — Тэннера коэффициент хищничества равен py/(q + y). Он не может превышать величины p/q и при неограниченном росте популяции жертв стремится, монотонно возрастая, к числу p/q, выражающему естественную потребность хищников в пище. В результате получается следующая система уравнений (модель Холлинга — Тэннера)
yy’ = [c – dy – px/(q + y)]y.
Системы уравнений, возникающие при описании биологических популяций, во многом близки к системам дифференциальных уравнений, описывающих кинетику химических реакций. К слову сказать, система Лотки — Вольтерры была первоначально выведена Лоткой как система, описывающая некоторую гипотетическую химическую реакцию (см. реакцию (6) ниже), и лишь позже Вольтерра вывел ее как систему, описывающую популяцию хищник — жертва.
Химическая кинетика описывает химические реакции с помощью так называемых стехиометрических уравнений. Простейший пример такого уравнения — это известное уравнение горения водорода: H2 + O2 = H2O. Общий вид стехиометрического уравнения химической реакции таков:
(натуральные числа ml и nl называются стехиометрическими коэффициентами). Это символическая запись химической реакции, в которой m1 молекул реагента X1, m2 молекул реагента X2, . mp молекул реагента Xp, вступив в реакцию образуют n1 молекул вещества Y1, n2 молекул вещества Y2, . nq молекул вещества Yq. Основной закон, выражающий скорость протекания реакции (5) — закон действующих масс — гласит: скорость протекания реакции пропорциональна концентрациям реагентов. Поэтому, если обозначить буквами xl, концентрации соответствующих веществ, то
здесь K — константа скорости протекания реакции (она обычно пишется в уравнении (5) над стрелкой и измеряется в моль–1·с–1).
Система Лотки — Вольтерры описывает гипотетическую трехстадийную реакцию вида
в которой концентрации a и b исходного реагента A и продукта реакции B поддерживаются постоянными (эта реакция является открытой в том смысле, что реактор обменивается веществами A и B с окружающей средой). Тогда в силу закона действующих масс
Последняя система с точностью до коэффициентов совпадает с моделью Лотки — Вольтерры (a = const). Несколько слов о том, как получается система (7) – (8). В первой реакции «со скоростью K1ax» исчезает одна молекула вещества X и с этой же скоростью появляются две молекулы этого вещества. Суммарная скорость изменения концентрации реагента X в результате первой реакции следовательно равна –K1ax + 2K1ax = K1ax. Во второй реакции, очевидно, концентрация X убывает со скоростью –K2xy. Наконец, в третьей реакции X не участвует. В итоге получается уравнение (7). Уравнение (8) выводится аналогично.
Системы уравнений химической кинетики, описывающие реакции, представляющие практических интерес, обычно имеют большие размерности, сильные нелинейности и малые сингулярно возмущающие параметры. Их численное исследование осложняется еще и тем, что эти системы, как правило, жесткие, что вынуждает разрабатывать специальные методы приближенного исследования.
Математическая модель эпидемии
Применение дифференциальных уравнений в медицине мы продемонстрируем на примере простейшей математической модели эпидемии. Отметим здесь же, что вышеописанные приложения дифференциальных уравнений в биологии и химии тоже имеют медицинский оттенок, поскольку в медицине важную роль играет исследование различных биологических популяций (например, популяции болезнетворных бактерий) и исследование химических реакций в организме (например, ферментативных).
В модели описывается распространение инфекционного заболевания в изолированной популяции. Особи популяции делятся на три класса. Инфицированный класс численностью x(t) (t — время) состоит из инфицированных (заболевших) особей, каждая из этих особей заразна (предполагается, что инкубационный период заболевания пренебрежимо короток). Второй класс численностью y(t) составляют восприимчивые особи, т. е. особи, которые могут заразиться при контакте с инфицированными особями. И, наконец, третий класс состоит из невосприимчивых особей (приобретших иммунитет или погибших в результате заболевания). Его численность обозначается z(t). Предполагается также, что общая численность популяции n постоянна (т. е. не учитываются рождения, естественные смерти и миграция). Две гипотезы, лежащие в основе модели таковы:
1) заболеваемость в момент времени t равна x(t)y(t) (эта гипотеза основывается на правдоподобном предположении, что число заболевающих пропорционально числу встреч между больными и восприимчивыми особями, которое в свою очередь в первом приближении пропорционально x( t)y(t)); таким образом численность класса x растет, а численность класса y убывает со скоростью ax(t)y(t) (a > 0);
2) численность становящихся невосприимчивыми особей (приобретших иммунитет или погибших) растет со скоростью, пропорциональной численности заболевших, т. е. со скоростью bx(t) (b > 0). В результате мы получаем систему уравнения:
Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Применение дифференциальных уравнений первого порядка для решения задач
Раздел 1. Математический анализ
Тема 1.4. Дифференциальные уравнения и их применения в медицине
1. Основные понятия и определения дифференциального уравнения.
2. Методы решения некоторых дифференциальных уравнений.
3. Применение дифференциальных уравнений первого порядка для решения задач.
Основные понятия и определения дифференциального уравнения
Опр. Равенство, связывающее независимую переменную х, неизвестную функцию у = f(x), а так же её производные y’,y”,….. y n , называется обыкновенным дифференциальным уравнением.
F(x,y.y’,y”………) = 0, где F – известная функция, заданная в некоторой фиксированной области; х – независимая переменная; у – зависимая переменная; y’,y”,….. y n – её производные.
Опр. Решением дифференциального уравнения называется функция у = f(x), которая будучи представлена в уравнении F(x,y.y’,y”………) = 0, обращает его в тождество. График этой функции называется интегральной кривой.
Пример 1.1. Дифференциальное уравнение
Представим в виде: 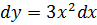
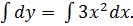
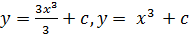
Методы решения некоторых дифференциальных уравнений
Выбор метода решения дифференциального уравнения зависит от его вида.
Дифференциальные уравнения первого порядка с разделяющимися переменными.
Уравнения вида 
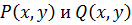
После резделения переменных, когда каждый член будет зависеть только от одной переменной, общий интеграл уравнения находится почленным интегрированием:
Решением этого уравнения будет:
Пример 2.1. Найти решение уравнения: 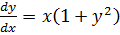
Разделим уравнение на множители, зависящие только от одной переменной:
Проинтегрируем левую и правую части:
Общее решение:
Линейные дифференциальные уравнения первого порядка.
Опр. Уравнения вида: 
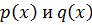
При 

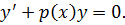
При 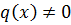

Применение дифференциальных уравнений первого порядка для решения задач
Этапы решения задач с помощью дифференциальных уравнений:
1. Оформить условия, в которых протекают изучаемые процессы;
2. Выбрать зависимые и независимые переменные;
3. Определить функциональные зависимости между ними
4. Решение уравнения;
5. Анализ полученных решений.
В уравнениях, описывающих медико-биологические процессы, в качестве независимой переменной чаще всего используется временная компонента.
Размножение бактерий
Если бактерии обитают в благоприятной среде, то скорость размножения бактерий пропорциональна размеру популяции. Такое предположение описывается дифференциальным уравнением: 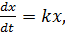


Вычислим определённые интегралы:
Получим экспоненциальную кривую, которая зависит от времени и k. Если 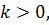
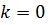
| N |
| N0 |
| k 0 |
| t |
Для определения значения k необходимо иметь дополнительные сведения об изменении численности бактерий за определённый промежуток времени.
Внутривенное введение глюкозы
При внутривенном введении с помощью капельницы скорость поступления глюкозы в кровь постоянна и равна с. В крови глюкоза разлагается и удаляется из кровеносной системы со скоростью, пропорциональной имеющемуся количеству глюкозы. Тогда дифференциальное уравнение, описывающее этот процесс, имеет вид: 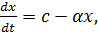
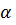
Это неоднородное линейное дифференциальное уравнение первого порядка, и его общее решение находиться по формуле:

Тогда 
Частное решение уравнения 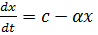
При увеличении времени уровень глюкозы в крови приближается к 
Видео:Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Тема: Дифференциальные уравнения и их применения . в медицинской практике
Тема: Дифференциальные уравнения и их применения
в медицинской практике
1. Основные понятия и определения дифференциального уравнения
2. Методы решения дифференциальных уравнений.
3. Применение дифференциальных уравнений для решения задач.
1.Основные понятия и определения дифференциального уравнения
Говоря о дифференциальных уравнениях мы должны дать определение дифференциального уравнения.
Опр.: Уравнения, в которых неизвестными являются не только сами функции, но и их производные называются дифференциальными уравнениями
Опр.: Если в уравнение входит независимая переменная, неизвестная функция и её первая производная, то это уравнение называется дифференциальным уравнением I-го порядка.
Опр.: Порядком дифференциального уравнения называется порядок старшей производной неизвестной функции, входящей в это уравнение.
Опр.: Решением дифференциального уравнения называют любую функцию при подстановке, которой в это уравнение получается тождество. Простейшим уравнением первого порядка является уравнение: У’=f (x)
-Что будет являться решением этого уравнения?
У=∫f(х)dx=F(x)+C – это общее решение.
-Как же выглядит геометрически общее решение?
 |
Геометрически общее решение представляет собой семейство интегральных кривых, т. е. совокупность линий, соответствующих различным значениям постоянной С.
Опр.: График решения дифференциального уравнения называют интегральной кривой этого уравнения.
Решение: y=5x+C –общее решение диф. уравнения
Зададим начальные условия : х0=0, у0=1 и подставим в общее решение соответственно вместо х и у.
Получаем у=5х+1-это частное решение дифференциального уравнения.
2.Методы решения дифференциальных уравнений
3.Применение дифференциальных уравнений для решения задач
Дифференциальные уравнения занимают важное место при решении задач физико-химического, фармацевтического и медико-биологического содержания. Пользуясь ими, мы устанавливаем связь между переменными величинами, характеризующими процесс или явление.
Решение любой задачи с помощью математического анализа можно разбить на три этапа:
1. перевод условий задачи на язык математики;
2. решение задачи;
3. оценка результатов.
Первая часть работы обычно заключается в составлении дифференциального уравнения и является наиболее трудной, так как общих методов составления дифференциальных уравнений нет и навыки в этой области могут быть приобретены лишь в результате конкретных примеров.
Закон растворения лекарственных форм вещества из таблеток
Скорость растворения лекарственных форм вещества из таблеток пропорциональна количеству лекарственных форм вещества в таблетке. Установить зависимость изменения количества лекарственных форм вещества в таблетке с течением времени.
Обозначим через m количество вещества в таблетке, оставшееся ко времени растворения t. Тогда
где k-постоянная скорости растворения. Минус в уравнении означает, что количество лекарственных форм вещества с течением времени убывает.
Закон размножения бактерий с течением времени
Скорость размножения некоторых бактерий пропорциональна количеству бактерий в данный момент. Установить зависимость изменения количества бактерий от времени.
Обозначим количество бактерий, имеющихся в данный момент, через х. Тогда
где k – коэффициент пропорциональности.
Закон роста клеток с течением времени
Для палочковидных клеток, у которых отношение поверхности клетки к её объёму сохраняется постоянным, скорость роста клетки
dl/dt пропорциональна длине клетки l в данный момент:
где α, β – постоянные, характеризующие процессы синтеза и распада.
Закон разрушения клеток в звуковом поле
Кавитация ультразвуковых волн проявляется в виде разрывов суспензионной среды и образования мельчайших пузырьков и пустот, плотность которых незначительна по сравнению с плотностью воды. Простейшие (бактерии, водоросли, дрожжи, лейкоциты, эритроциты) могут быть разрушены при кавитации, возникающей в интенсивном звуковом поле. Относительные скорости разрушения биологических клеток различных видов остаются постоянными в очень широком диапазоне частот. Эти скорости могут характеризовать относительную хрупкость клеток различных видов. Чтобы выразить это количественно, нужно определить скорость разрушения клетки в постоянном звуковом поле. Изучение этого вопроса показывает, что, пока по крайней мере 1% популяции остаётся неразрушенным, можно записать:
где N – концентрация клеток; t –время; R — постоянная
В теории эпидемий при условии, что изучаемое заболевание носит длительный характер, процесс передачи инфекции значительно более быстрый, чем течение самой болезни, и зараженные особи не удаляются из колонии и передают при встречах инфекцию незараженным особям.
Пусть в начальный момент t=0, а – число зараженных, b – число незараженных особей, x(t), y(t) – соответственно число зараженных и незараженных особей к моменту времени t. В любой момент времени t для промежутка, меньшего времени жизни одного поколения, имеет место равенство
При этих условиях нужно установить закон изменения числа незаражённых особей с течением времени, т. е. найти y=f(x).
Так как инфекция передаётся при встречах зараженных особей с незараженными, то число незараженных особей будет убывать с течением времени пропорционально количеству встреч между зараженными и незараженными особями. Для промежутка времени dt dy=-βxy,
откуда dy/dt= — βxy, где β – коэффициент пропорциональности. Подставив в это уравнение значение х из равенства (1), получим дифференциальное уравнение с разделяющимися переменными:
Контрольные вопросы для закрепления:
1. Дайте понятие дифференциальному уравнению, его решению.
2. Назовите методы решения дифференциальных уравнений, охарактеризуйте каждый.
3. Приведете примеры обыкновенного дифференциального уравнения, уравнения с разделяющими переменными, линейного.
4. Приведите примеры дифференциального уравнения первого, второго, третьего порядка.
5. Каково практическое применение дифференциальных уравнений.
1., Демидова : Компьютерные технологии в медицине. – Ростов н/Д:Феникс, 2008. -588 с. Ил.-(Среднее профессиональное образование)
🎥 Видео
Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Дифференциальные уравнения. 11 класс.Скачать

Поле направлений дифференциального уравнения первого порядкаСкачать

Простейшие дифференциальные уравненияСкачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

"Мы зажигаем свои звёзды" О роли нелинейных дифференциальных уравненийСкачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

4. Однородные дифференциальные уравнения (часть 1)Скачать

6. Особые решения ДУ первого порядкаСкачать