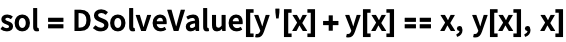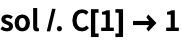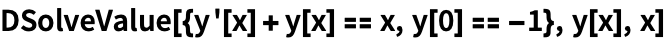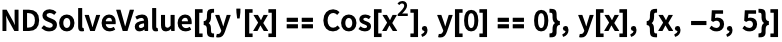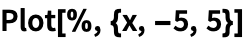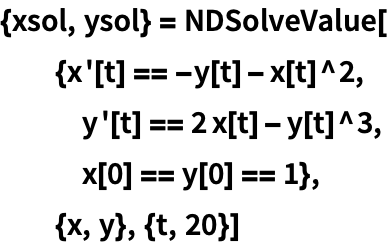Данная задача возникает при поиске частного решения дифференциального уравнения. Наш онлайн калькулятор, построенные на основе системы Wolfram Alpha, позволяет найти решение задачи Коши для различных типов дифференциальных уравнений. Чтобы начать работу, необходимо ввести данные своей задачи (дифференциальное уравнение и начальные условия) в калькулятор.
Найти решение задачи Коши для дифференциального уравнения:
при заданных начальных условиях:
При постановке задачи Коши, указываются так называемые начальные условия, позволяющие однозначно выделить искомое частное решение из общего. Эти условия включают в себя значения функции и всех её производных до включительно (где -порядок дифференциального уравнения), заданные в одной и той же точке .
Поясним вышесказанное на конкретном примере. Пусть нам требуется найти частное решение дифференциального уравнения:
удовлетворяющее начальным условиям:
Первым делом, используя различные методы (Бернули, вариации произвольной постоянной Лагранжа), сначала находим общее решение данного дифференциального уравнения:
Теперь, для поиска частного решения, нам необходимо использовать заданные начальные условия. Для этого, находим производную функции полученной ранее:
Далее, поставляем начальные условия в функцию и её производную :
Решая полученную систему уравнений получаем значения произвольных постоянных и :
Подставляем полученные результаты в общее решение дифференциального уравнения, в результате получаем искомое частное решение:
Видео:How to Find the Derivative of a Function Using Wolfram|AlphaСкачать
Другие полезные разделы:
Видео:Wolframalpha : решение любых задач для студента по алгебре, вышке, физике, дифференциальные ур. и прСкачать
Оставить свой комментарий:
Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме
Видео:Как решить любую задачу студенту? : Интеллектуальный поисковик wolframalpha.comСкачать
WolframAlpha по-русски
Математика с WolframAlpha ® . Объяснения с примерами.
Решение обыкновенных дифференциальных уравнений в Wolfram|Alpha
Решение дифференциальных уравнений с выводом результатов в пошаговом представлении (функция «Show steps» — Показать шаги) является одной из важных особенностей Wolfram|Alpha.
Wolfram|Alpha в большинстве случаев может помочь в решении дифференциальных уравнений различного уровня сложности, начиная от простейших дифференциальных уравнений первого порядка с разделяющимися переменными (separable equations ) и включая более сложные уравнения, для решения которых служат, например, методы операционного исчисления, использующие преобразование Лапласа.
Чтобы решить дифференциальное уравнение с помощью Wolfram|Alpha достаточно ввести его в систему. ВНИМАНИЕ! Для ввода символа производной используется знак апострофа » ‘ «, но не кавычки (!). Для определенности можно добавить перед уравнением поисковое предписание solve (хотя, во многих случаях, это и не обязательно).
- solve xy’+y=2x
Как видим, Wolfram|Alpha сначала определяет (классифицирует) этот пример, как обыкновенное линейное дифференциальное уравнение первого порядка, затем выводит общее решение данного уравнения, график частного решения, удовлетворяющего условию y(1)=1, а также семейство интегральных кривых данного уравнения.
Чтобы получить детальное пошаговое решение, используйте кнопку «Show steps»:
Аналогичным образом можно получить решение, например, дифференциального уравнения Бернулли:
- solve 2xy’+y=x^2y^3
- solve y’-2y/x=-x^2y^2
Wolfram|Alpha позволяет также получать решения дифференциальных уравнений второго и высших порядков. Например, так выглядит решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами:
- solve y» + 2y’ +y= 54x^2e^(2x)sin(3x)
Или же дифференциального уравнения 3-го порядка: solve y»» = y.
С помощью Wolfram|Alpha возможно получить общее решение дифференциального уравнения, заданного в общем виде:
- solve a*y»(x)+b*y'(x)+c*y(x)=0
Наконец, в некоторых случаях, когда это необходимо,Wolfram|Alpha использует для решения дифференциальных уравнений методы операционного исчисления (преобразование Лапласа):
- solve y»(x)-2y'(x)/x+y(x)=0
Подробное решение этого примера смотрите по этой ссылке.
Видео:Решение физических задач с помощью дифференциальных уравненийСкачать
Дифференциальные уравнения
Язык Wolfram позволяет решать обыкновенные дифференциальные уравнения, дифференциальные уравнения в частных производных и уравнения с запаздыванием.
Функция DSolveValue возвращает решение дифференциального уравнения в общем виде:
| Out[1]= |  |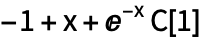
Используем символ /. для замены константы:
| Out[2]= |  |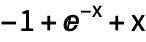
Или добавим начальные условия для получения частного решения:
| Out[3]= |  |
Функция NDSolveValue позволяет находить численные решения:
| Out[1]= |  |
Объект InterpolatingFunction можно визуализировать без дополнительной обработки:
| Out[2]= |  |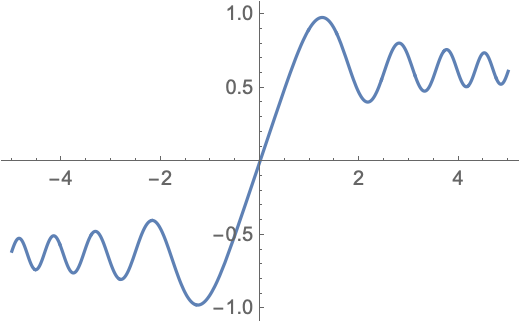
Для решения систем дифференциальных уравнений, необходимо использовать списки для задания уравнений и условий:
(Обратите внимание, что перенос уравнений на новую строку не влияет на результат.)
| Out[1]= |  |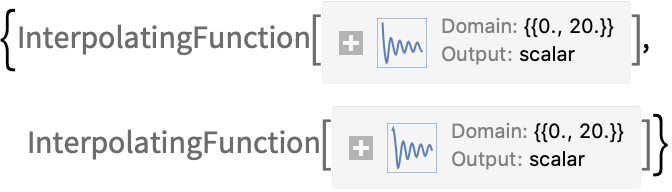
Построим решения системы в виде параметрического графика:
🔍 Видео
13. Как решить дифференциальное уравнение первого порядка?Скачать
КиЯ 0.18 | Решение уравнения и отображение его корней в Wolfram LanguageСкачать
Дифференциальные уравнения. 11 класс.Скачать
Новое в Wolfram Language | Аналитическое решение уравнений в частных производныхСкачать
Частное решение дифференциального уравнения. 11 класс.Скачать
7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
Сеточные методы решения дифференциальных уравнений в частных производных.Скачать
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
