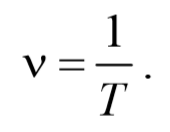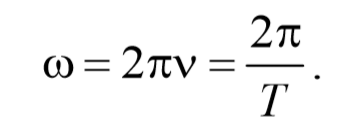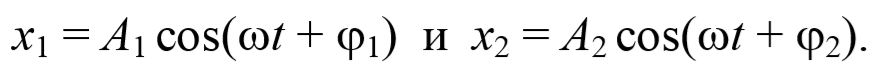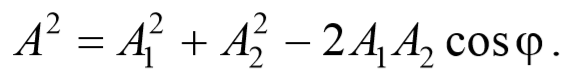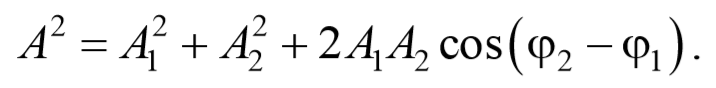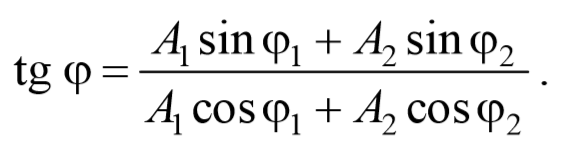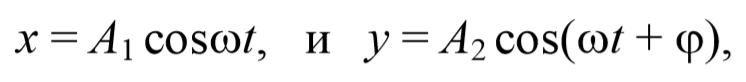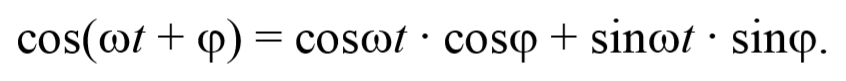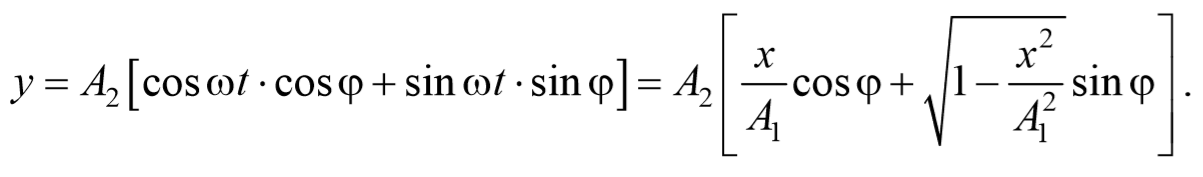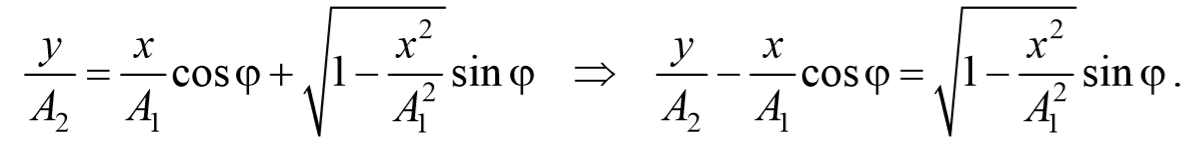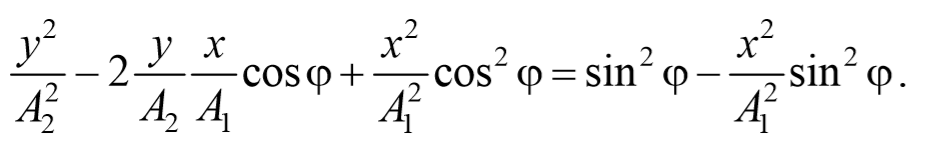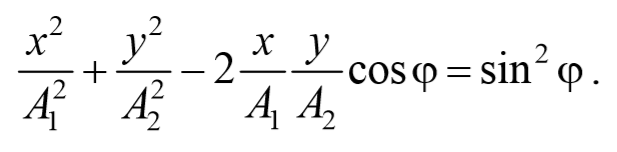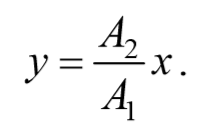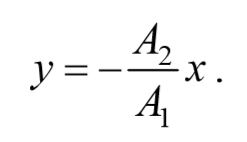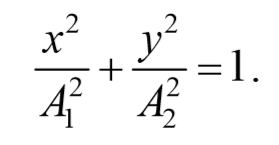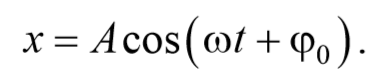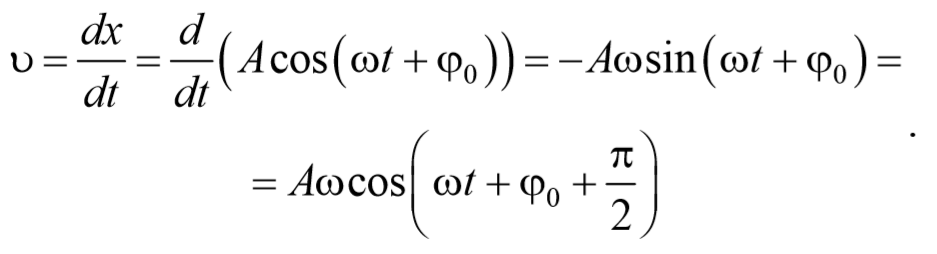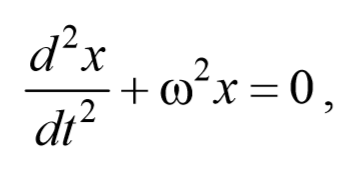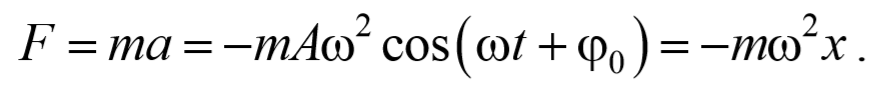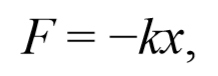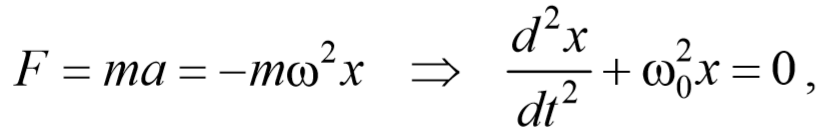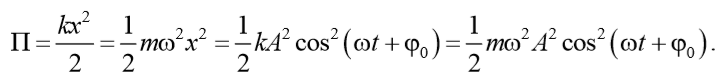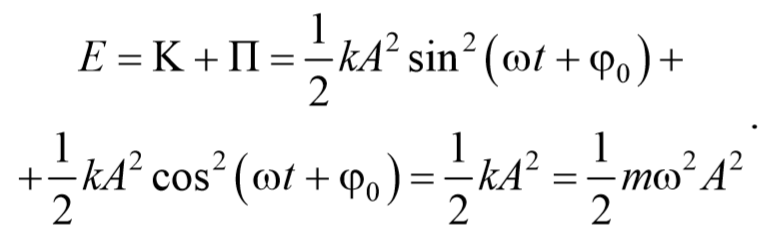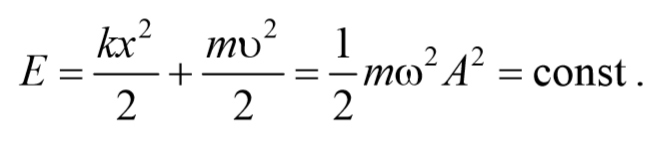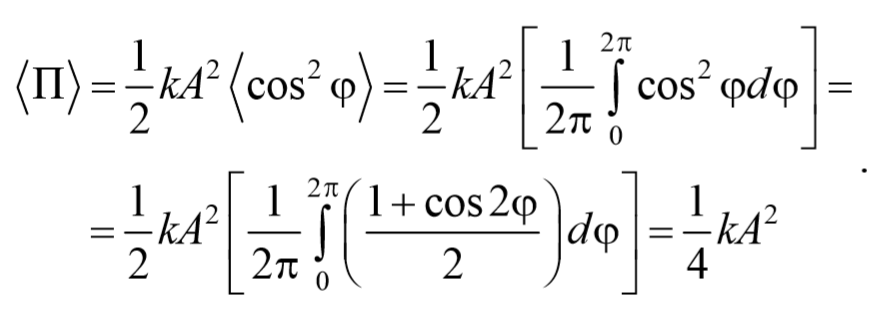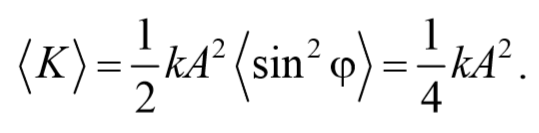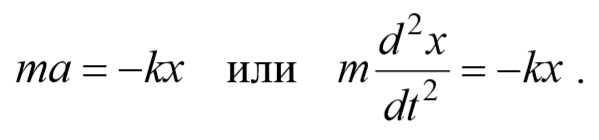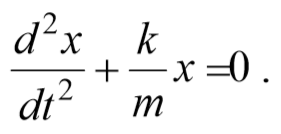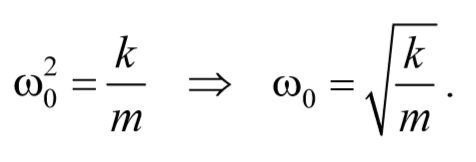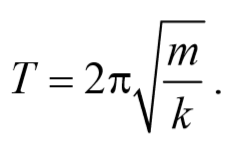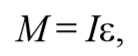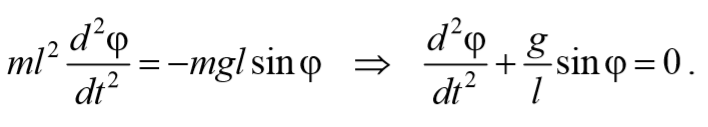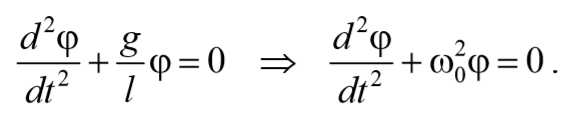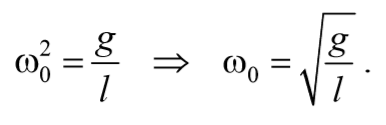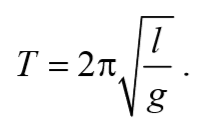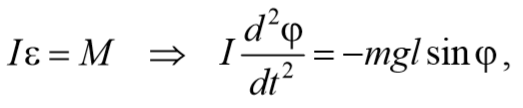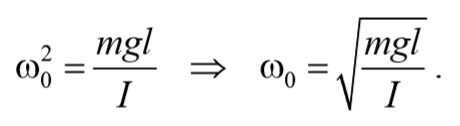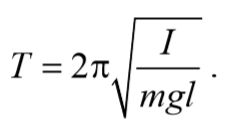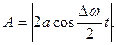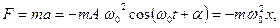Решение дифференциальных уравнений на гармонический осциллятор (7 видео)

Лекция №7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Содержание

5.1. Свободные гармонические колебания и их характеристики.
5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.
5.3. Дифференциальное уравнение гармонических колебаний и его решение.
5.4. Энергия гармонических колебаний.
5.5. Пружинный, математический и физический маятники.
Идеальный гармонический осциллятор. Уравнение идеального осциллятора и его решение. Амплитуда, частота и фаза колебаний
💥 Видео

5.1. Свободные гармонические колебания и их характеристики.

Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени. Наиболее важными характеристиками колебания являются: смещение, амплитуда, период, частота, циклическая частота, фаза.

Простейший вид периодических колебаний − это гармонические колебания. Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид

1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени.

2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.

3) Период колебаний T − это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Единица измерения [T] = 1 с .

За период система совершает одно полное колебание.

4) Частота колебаний ν − это величина, равная числу колебаний, совершаемых в единицу времени (за 1 секунду). Единица измерения [ν]= 1 Гц . Частота определяется по формуле

5) Циклическая частота ω − это величина, равная числу полных колебаний, совершающихся за 2π секунд. За единицу циклической частоты принята угловая частота, при которой за время 1 с совершается 2π циклов колебаний, [ω]= с -1 . Циклическая частота связана с периодом и частотой колебаний соотношением

6) Фаза колебаний ωt + φ₀ − фаза указывает местоположение колеблющейся точки в данный момент времени.

7) Начальная фаза φ₀ − указывает местоположение колеблющейся точки в момент времени t = 0 .

5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.

Сложение нескольких колебаний одинакового направления можно изображать графически с помощью метода векторной диаграммы.

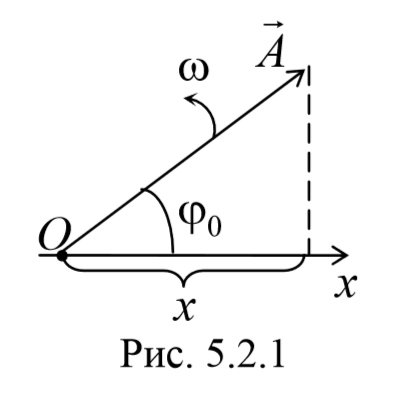
Гармоническое колебание может быть представлено графически с помощью вращающегося вектора амплитуды А . Для этого из произвольной точки O , выбранной на оси Ox , под углом φ₀ , равным начальной фазе колебания, откладывается вектор амплитуды А . Модуль этого вектора равен амплитуде рассматриваемого колебания. Если этот вектор привести во вращение с угловой скоростью ω , равной циклической частоте колебаний, то проекция конца вектора амплитуды будет перемещаться по оси Ox и принимать значения от -A до +A , а колеблющаяся величина изменяться со временем по закону x = Acos(ωt + φ₀)

1. Сложение одинаково направленных гармонических колебаний.

Сложим два гармонических колебания одинакового направления и одинаковой частоты. Смещение x колеблющегося тела будет суммой смещений x₁ и x₂ , которые запишутся следующим образом:

Представим оба колебания на векторной диаграмме. Построим по правилу сложения векторов результирующий вектор А . Проекция этого вектора на ось Ox равна сумме проекций слагаемых векторов x=x₂+x₂ , следовательно, вектор А представляет собой результирующее колебание. Определим результирующий вектор амплитуды А потеореме косинусов

Так как угол между векторами А ₁ и А ₂ равен φ=π-(φ₂-φ₁) , то cos[π-(φ₂-φ₁)]=-cos(φ₂-φ₁) , следовательно, результирующая амплитуда колебания будет равна

Определим начальную фазу результирующего колебания.

Из рисунка видно, что начальная фаза результирующего колебания

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармонические колебания в том же направлении и с той же частотой.

2. Сложение взаимно перпендикулярных гармонических колебаний.

Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимно перпендикулярных направлениях. Допустим, что материальная точка совершает колебания как вдоль оси X , так и вдоль оси Y . Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний примут вид

где φ − разность фаз обоих колебаний.

Уравнение траектории получим, исключив из уравнений (5.2.6) параметр времени t: cosωt= $$xover A_1$$ , а sinωt= $$sqrt=sqrt$$ Разложим косинус во втором из уравнений (5.2.6)

Перепишем это уравнение в следующем виде

После преобразования, получим

Используя тригонометрическое тождество cos 2 φ+sin 2 φ=1 , окончательно получим

Это есть уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разности фаз.

Рассмотрим несколько частных случаев и определим форму траектории для них:

a) разность фаз равна нулю [φ=0]

В этом случае $$( — )^2=0$$ , откуда получается уравнение прямой

Видео:Микролекция: Гармонический осцилляторСкачать

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой $$A= sqrt<A_1+A_2>$$ .

2) разность фаз равна ±π[φ=±π] .

В этом случае $$( — )^2=0$$ , откуда получается уравнение прямой

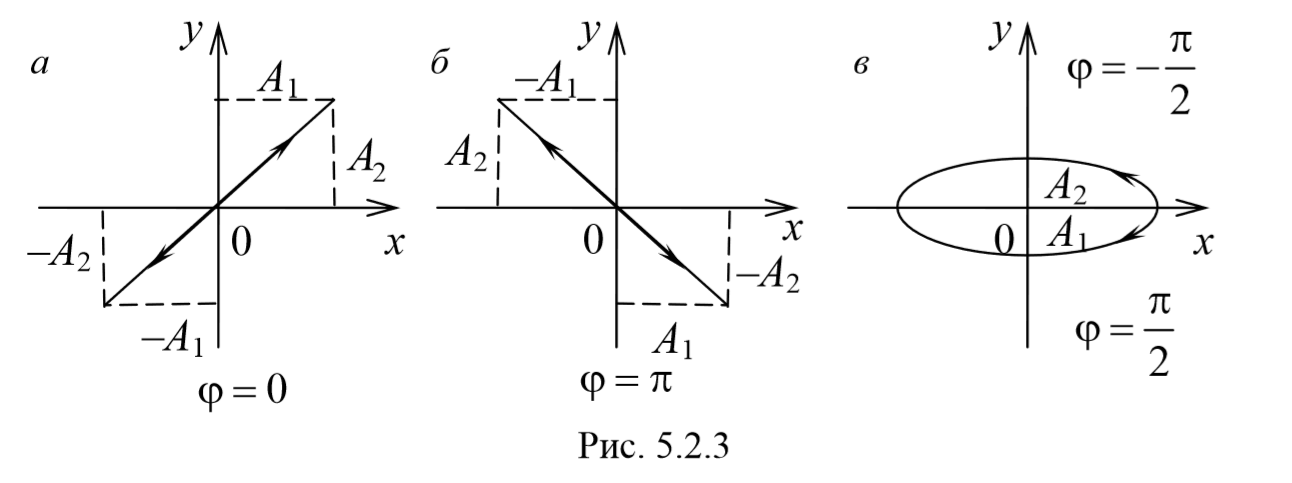
3) Разность фаз равна ± $$πover 2$$ [φ=± $$π over2$$ ] . Тогда

Уравнение эллипса, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд колебаний эллипс вырождается в окружность. Случаи φ=+ $$πover 2$$ и φ=- $$πover 2$$ отличаются направлением движения. Если φ=+ $$πover 2$$ , то уравнения колебаний имеют следующий вид: x=A₁cosωt , и y=-A₂sinωt и движение совершается по часовой стрелке. Если φ=- $$πover 2$$ , , то уравнения колебаний имеют следующий вид: x=A₁cosωt , и y=A₂sinωt и движение совершается против часовой стрелке.

Рассмотренные три частных случая представлены на рис. 5.2.3, а, б, в. Рис

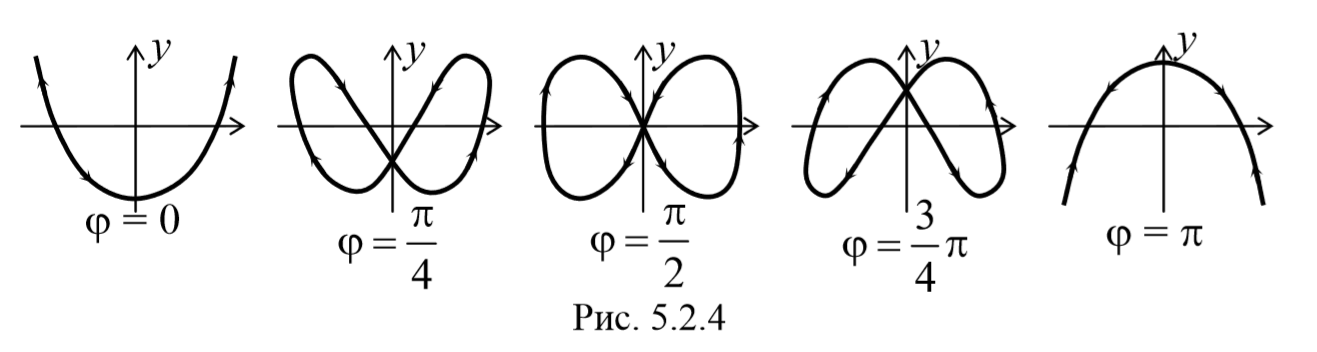
4) Если частоты складываемых взаимно перпендикулярных колебаний различны, то траектория результирующего движения имеет вид сложных кривых, называемых фигурами Лиссажу . Форма этих кривых определяется соотношением амплитуд, частот и разности фаз складываемых колебаний.

На рис. 5.2.4 показаны фигуры Лиссажу, которые получаются при соотношении частот 1:2 и различной разности фаз колебаний.

По виду фигур можно определить неизвестную частоту по известной частоте или определить соотношение частот складываемых колебаний.

5.3. Дифференциальное уравнение гармонических колебаний и его решение.

Продифференцируем по времени уравнение гармонических колебаний

и получим выражение для скорости

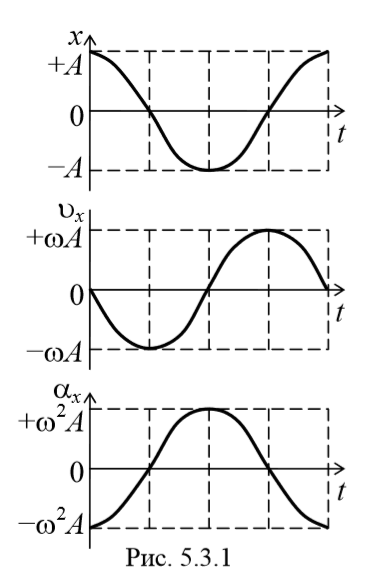
Из сравнения уравнений (5.3.1) и (5.3.2) следует, что скорость опережает смещение по фазе на π/2 . Амплитуда скорости равна Аω .

Продифференцировав уравнение (2) еще раз по времени, получим выражение для ускорения

Как следует из уравнения (5.3.3), ускорение и смещение находятся в противофазе. Это означает, что в тот момент времени, когда смещение достигает наибольшего, положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Амплитуда ускорения равна Аω 2 (рис. 5.3.1).

Из выражения (5.3.3) следует дифференциальное уравнение гармонических колебаний

Результирующая сила, действующая на материальную точку массой m , определяется с помощью второго закона Ньютона. Проекция этой силы

Эта сила пропорциональна смещению точки из положения равновесия и направлена в сторону противоположную этому смещению, т. е. она стремится вернуть точку в положение равновесия, и поэтому называется возвращающей силой . Таким образом, гармонические колебания происходят под действием силы F , пропорциональной смещению x и направленной к положению равновесия,

где k=mω 2 − постоянный коэффициент. Возвращающая сила подобна упругим силам, возникающим в телах при их деформации. Такая зависимость силы от смещения характерна для упругой силы, поэтому силы иной физической природы, удовлетворяющие зависимости (5.3.6) называются квазиупругими силами .

Материальная точка, совершающая колебания под действием квазиупругой силы, называется линейным осциллятором . Ее динамическое поведение описывается дифференциальным уравнением

ω₀ − собственная частота осциллятора.

Решение этого уравнения дает закон движения линейного осциллятора x=Acos(ωt+φ₀) .

5.4. Энергия гармонических колебаний.

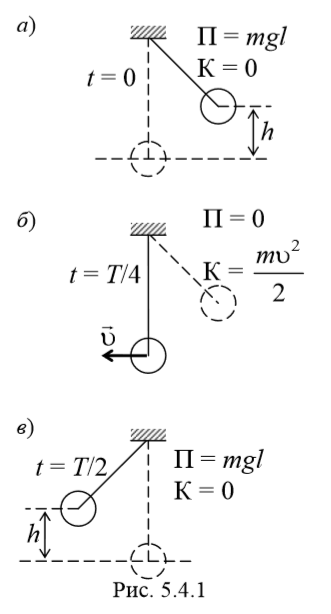
В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.

Потенциальная энергия тела, совершающего гармонические колебания равна

Кинетическая энергия тела, совершающего гармонические колебания равна

Таким образом, полная энергия гармонического колебания, состоящая из суммы кинетической и потенциальной энергий, определяется следующим образом

Следовательно, полная энергия гармонического колебания

оказывается постоянной в случае гармонических колебаний.

Найдем среднее значение потенциальной энергии за период колебания

Аналогично получается для среднего значение кинетической энергии

Таким образом, и потенциальная, и кинетическая энергии изменяются относительно своих средних значений по гармоническому закону с частотой 2ω и амплитудой ωt kA 2

5.5. Пружинный, математический и физический маятники.

Рассмотрим несколько простейших систем, совершающих свободные гармонические колебания.

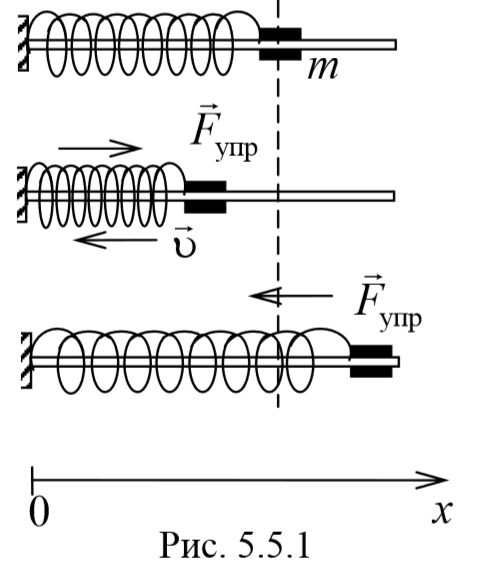
1) Пружинный маятник − это материальная точка массой m , подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жесткостью k и совершающий гармонические колебания под действием упругой силы. Пусть шайба массой m , прикрепленная к пружине, совершает колебания. Для составления дифференциального уравнения колебаний запишем второй закон Ньютона в проекции на ось Ox F_упр=ma . Упругая сила F_упр=-kx . Приравнивая последние два уравнения и, используя определение ускорения тела, получим

Видео:Гармонический осциллятор. Груз на пружине. 3 метода решения.Скачать

Сравнивая уравнения (5.3.7) и (5.5.2) получаем, что пружинный маятник совершает гармонические колебания с частотой

Так как период колебаний определяется по формуле T= $$2πover ω_0$$ , то период колебаний пружинного маятника

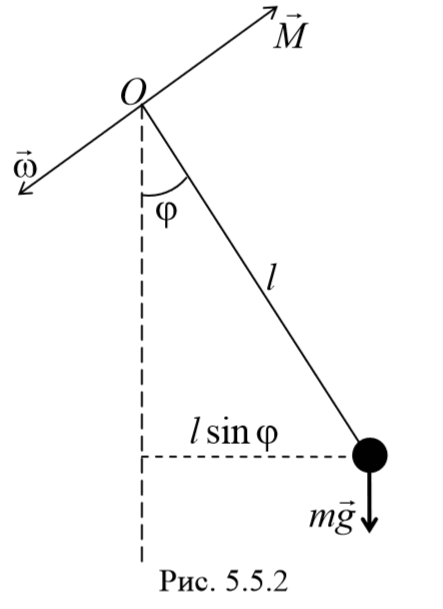
2) Математический маятник − это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка массой m . Отклонение маятника от положения равновесия будем характеризовать углом φ , образованным нитью с вертикалью.

При отклонении маятника от положения равновесия возникает вращательный момент M , равный по величине mqlsinφ .Он имее акое же направление, что стремится вернуть маятник в положение равновесия. Следовательно, выражение для вращательного момента имеет вид: M=-mqlsinφ . Применим основно ательного движения

где L=ml 2 − момент инерции материальной точки. Тогда, учитывая, что угловое ускорение ε= $$d^2φover dt^2$$ , получим

Если рассматривать малые колебания, то sinφ≈φ . Получим

То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой

Период колебаний математического маятника

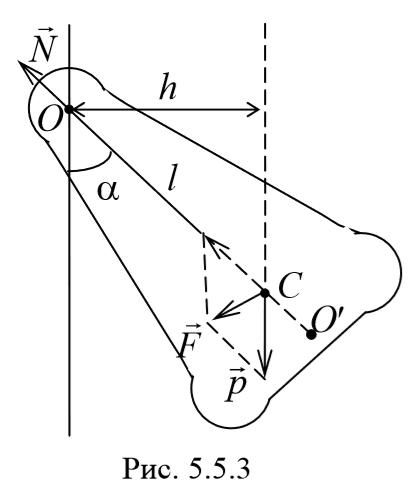
3) Физический маятник − это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. При отклонении маятника от положения равновесия на угол φ возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен M=-mglsinφ .

Согласно основному уравнению динамики вращательного движения получаем

где I − момент инерции маятника относительно оси, проходящей через точку подвеса.

Если рассматривать малые колебания, то sinφ≈φ . Получим

Период колебаний математического маятника

Из сопоставления формул периодов колебаний математического и физического маятников T=2π $$sqrt$$ и T=2π $$sqrt$$ получается, что математический маятник с длиной

будет иметь такой же период колебаний, что и данный физический маятник.

Величина l_пр (отрезок OO′) называется приведенной длиной физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, и лежащая на расстоянии приведенной длины от оси вращения, называется центром качания (О′) физического маятника. Точка подвеса О и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.

Идеальный гармонический осциллятор. Уравнение идеального осциллятора и его решение. Амплитуда, частота и фаза колебаний

КОЛЕБАНИЯ. ВОЛНЫ. ОПТИКА

КОЛЕБАНИЯ

Лекция 1

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Идеальный гармонический осциллятор. Уравнение идеального осциллятора и его решение. Амплитуда, частота и фаза колебаний

Колебание – один из самых распространённых процессов в природе и технике. Колебания – это процессы, повторяющиеся во времени. Колеблются высотные здания и высоковольтные провода под действием ветра, маятник заведённых часов и автомобиль на рессорах во время движения, уровень реки в течение года и температура человеческого тела при болезни. Звук – это колебания давления воздуха, радиоволны – периодические изменения напряжённости электрического и магнитного поля, свет – это тоже электромагнитные колебания. Землетрясения – колебания почвы, приливы и отливы – изменение уровней морей и океанов, вызываемые притяжением луны и т.д.

Колебания бывают механические, электромагнитные, химические, термодинамические и др. Несмотря на такое многообразие, все колебания описываются одними и теми же дифференциальными уравнениями.

Первыми учёными, изучавшими колебания, были Галилео Галилей и Христиан Гюйгенс. Галилей установил независимость периода колебаний от амплитуды. Гюйгенс изобрёл часы с маятником.

Любая система, которая, будучи слегка выведена из положения равновесия, совершает устойчивые колебания, называется гармоническим осциллятором. В классической физике такими системами являются математический маятник в пределах малых углов отклонения, груз в пределах малых амплитуд колебаний, электрический контур, состоящий из линейных элементов ёмкости и индуктивности.

Гармонический осциллятор можно считать линейным, если смещение от положения равновесия прямо пропорционально возмущающей силе. Частота колебаний гармонического осциллятора не зависит от амплитуды. Для осциллятора выполняется принцип суперпозиции — если действуют несколько возмущающих сил, то эффект их суммарного действия может быть получен как результат сложения эффектов от действующих сил в отдельности.

Гармонические колебания описываются уравнением (рис.1.1.1)

(1.1.1)

где х -смещение колеблющейся величины от положения равновесия, А – амплитуда колебаний, равная величине максимального смещения, — фаза колебаний, определяющая смещение в момент времени , — начальная фаза, определяющая величину смещения в начальный момент времени, — циклическая частота колебаний.

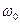
Время одного полного колебания называется периодом, , где — число колебаний, совершенных за время .

Частота колебаний определяет число колебаний, совершаемых в единицу времени, она связана с циклической частотой соотношением , тогда период .

Скорость колеблющейся материальной точки

. (1.1.2)

Таким образом, скорость и ускорение гармонического осциллятора также изменяются по гармоническому закону с амплитудами и соответственно. При этом скорость опережает по фазе смещение на , а ускорение – на (рис.1.1.2).

Из сопоставления уравнений движения гармонического осциллятора (1.1.1) и (1.1.2) следует, что , или

. (1.1.3)

Это дифференциальное уравнение второго порядка называется уравнением гармонического осциллятора. Его решение содержит два постоянные а и , которые определяются заданием начальных условий

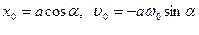
Отсюда .

Если периодически повторяющийся процесс описывается уравнениями, не совпадающими с (1.1.1), он н6азывается ангармоническим. Система, совершающая ангармонические колебания, называется ангармоническим осциллятором.

1.1.2. Свободные колебания систем с одной степенью свободы. Комплексная форма представления гармонических колебаний

В природе очень распространены малые колебания, которые система совершает вблизи своего положения равновесия. Если система, выведенная из положения равновесия, предоставлена себе, то есть на неё не действуют внешние силы, то такая система будет совершать свободные незатухающие колебания. Рассмотрим систему с одной степенью свободы.

Устойчивому равновесию соответствует такое положение системы, в котором её потенциальная энергия имеет минимум (q – обобщённая координата системы). Отклонение системы от положения равновесия приводит к возникновению силы , которая стремится вернуть систему обратно. Значение обобщённой координаты, соответствующей положению равновесия, обозначим , тогда отклонение от положения равновесия

Будем отсчитывать потенциальную энергию от минимального значения . Примем Полученную функцию разложим в ряд Маклорена и оставим первый член разложения, имеем: о

где . Тогда с учётом введённых обозначений:

, (1.1.4)

С учётом выражения (1.1.4) для силы, действующей на систему, получаем:

Согласно второму закону Ньютона, уравнение движения системы имеет вид: ,

, (1.1.5)

Видео:Урок 327. Гармонические колебанияСкачать

Выражений (1.1.5) совпадает с уравнением (1.1.3) свободных гармонических колебаний при условии, что

, (1.1.6)

и имеет два независимых решения: и , так что общее решение:

, или

где

Из формулы (1.1.6) следует, что частота определяется только собственными свойствами механической системы и не зависит от амплитуды и от начальных условий движения.

Зависимость координаты колеблющейся системы от времени можно определить в виде вещественной части комплексного выражения 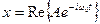, где A=Xe-iα– комплексная амплитуда, её модуль совпадает с обычной амплитудой, а аргумент – с начальной фазой.

1.1.3. Примеры колебательных движений различной физической природы

Колебания груза на пружине

Рассмотрим колебания груза на пружине, при условии, что пружина не деформирована за пределы упругости. Покажем, что такой груз будет совершать гармонические колебания относительно положения равновесия (рис.1.1.3). Действительно, согласно закону Гука, сжатая или растянутая пружина создаёт гармоническую силу:

где – коэффициент жёсткости пружины, – координата положения равновесия, х – координата груза (материальной точки) в момент времени , — смещение от положения равновесия.

Поместим начало отсчета координаты в положение равновесия системы. В этом случае .

Если пружину растянуть на величину х, после чего отпустить в момент времени t=0, то уравнение движения груза согласно второму закону Ньютона примет вид -kx =ma, или , и

(1.1.6)

Это уравнение совпадает по виду с уравнением движения (1.1.3) системы, совершающей гармонические колебания, его решение будем искать в виде:

. (1.1.7)

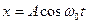
Подставим (1.17) в (1.1.6), имеем: 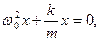то есть выражение (1.1.7) является решением уравнения (1.1.6) при условии, что

Если в начальный момент времени положение груза было произвольным, то уравнение движения примет вид:

Рассмотрим, как меняется энергия груза, совершающего гармонические колебания в отсутствие внешних сил (рис.1.14). Если в момент времени t=0 грузу сообщить смещение х=А, то его полная энергия станет равной потенциальной энергии деформированной пружины , кинетическая энергия равна нулю (точка 1).

На груз действует сила F= -kx, стремящаяся вернуть его в положение равновесия, поэтому груз движется с ускорением и увеличивает свою скорость, а, следовательно, и кинетическую энергию. Эта сила сокращает смещение груза х, потенциальная энергия груза убывает, переходя в кинетическую. Система «груз — пружина» замкнутая, поэтому её полная энергия сохраняется, то есть:

. (1.1.8)

В момент времени груз находится в положении равновесия (точка 2), его потенциальная энергия равна нулю, а кинетическая максимальна . Максимальную скорость груза найдём из закона сохранения энергии (1.1.8):

За счёт запаса кинетической энергии груз совершает работу против упругой силы – и пролетает положение равновесия. Кинетическая энергия постепенно переходит в потенциальную. При груз имеет максимальное отрицательное смещение –А, кинетическая энергия Wk=0, груз останавливается и начинает движение к положению равновесия под действием упругой силы F= -kx. Далее движение происходит аналогично.

Маятники

Под маятником понимают твёрдое тело, которое совершает под действием силы тяжести колебания вокруг неподвижной точки или оси. Различают физический и математический маятники.

Математический маятник – это идеализированная система, состоящая из невесомой нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной материальной точке.

Математическим маятником, например, является шарик на длинной тонкой нити.

Отклонение маятника от положения равновесия характеризуется углом φ, который образует нить с вертикалью (рис.1.15). При отклонении маятника от положения равновесия возникает момент внешних сил (силы тяжести) : , где m – масса, – длина маятника

Этот момент стремится вернуть маятник в положение равновесия (аналогично квазиупругой силе) и направлен противоположно смещению φ, поэтому в формуле стоит знак «минус».

Уравнение динамики вращательного движения для маятника имеет вид: Iε= ,

Будем рассматривать случай малых колебаний, поэтому sin φ ≈φ, обозначим ,

имеем: , или , и окончательно

Это уравнение гармонических колебаний, его решение:

Частота колебаний математического маятника определяется только его длиной и ускорением силы тяжести, и не зависит от массы маятника. Период равен:

Если колеблющееся тело нельзя представить, как материальную точку, то маятник называют физическим (рис.1.1.6). Уравнение его движения запишем в виде:

В случае малых колебаний , или =0 , где . Это уравнение движения тела, совершающего гармонические колебания. Частота колебаний физического маятника зависит от его массы, длины и момента инерции относительно оси, проходящей через точку подвеса.

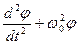
Обозначим . Величина называется приведённой длинной физического маятника. Это длина математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведённой длины от оси вращения, называется центром качания физического маятника (О’). Если маятник подвесить в центре качания, то приведённая длина и период колебаний будут теми же, что и в точке О. Таким образом, точка подвеса и центр качания обладают свойствами взаимности: при переносе точки подвеса в центр качения прежняя точка подвеса становится новым центром качения.

Математический маятник, который качается с таким же периодом, как и рассматриваемый физический, называется изохронным данному физическому маятнику.

1.1.4. Сложение колебаний (биения, фигуры Лиссажу). Векторное описание сложения колебаний

Сложение одинаково направленных колебаний можно производить методом векторных диаграмм. Любое гармоническое колебание можно представить в виде вектора следующим образом. Выберем ось х с началом отсчета в точке О (рис.1.1.7)

Из точки О построим вектор , который составляет угол с осью х. Пусть этот вектор поворачивается с угловой скоростью . Проекция вектора на ось Х равна:

то есть она совершает гармонические колебания с амплитудой а.

Рассмотрим два гармонических колебания одинакового направления и одинаковой циклической малой , заданные векторами и . Смещения по оси Х равны:

результирующий вектор имеет проекцию и представляет собой результирующее колебание (рис.1.1.8), по теореме косинусов Таким образом, сложение гармонических колебаний производится сложением векторов.

Проведем сложение взаимно перпендикулярных колебаний. Пусть материальная точка совершает два взаимно перпендикулярных колебания частотой :

Сама материальная точка при этом будет двигаться по некоторой криволинейной траектории.

Из уравнения движения следует: ,

. (1.1.9)

Из уравнения (1.1.9) можно получить уравнение эллипса (рис.1.1.9):

Рассмотрим частные случаи этого уравнения:

1. Разность фаз колебаний α= 0. При этом т.е. или Это уравнение прямой, и результирующее колебание происходит вдоль этой прямой с амплитудой (рис.1.1.10).

2. Если разность фаз то уравнение (1.1.9) переходит в уравнение эллипса, приведенного к координатным осям, При материальная точка движется по окружности, уравнение которой (рис.1.1.11).

3. Если частоты колебаний неодинаковы, то материальная точка описывает фигуры Лиссажу (рис.1112).

Рассмотрим сложение колебаний одного направления, частоты которых мало отличаются друг от друга. В этом случае результирующее движение можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такие колебания называются биениями.

Пусть частота одного колебания , второго . Амплитуды обоих колебаний одинаковы и равны а. Начальные фазы равны нулю. В таком случае уравнения колебаний имеют вид:

Сложим эти выражения:

(1.1.10)

График функции х(t) представлен на рис. 1.1.13. Множитель меняется гораздо медленнее, чем , поэтому (1.1.10) можно рассматривать как гармоническое колебание частоты , амплитуда которого меняется по некоторому периодическому закону

Частота изменения амплитуды – частота биений – равна разности частот складываемых колебаний .

Энергия колебаний

Смещение колеблющейся точки от положения равновесия, описывается уравнением:

ее ускорение равно второй производной от смещения по времени тогда сила, действующая на колеблющуюся точку, по второму закону Ньютона равна

— то есть сила пропорциональна смещению х и направлена против смещения к положению равновесия. Эта сила называется возвращающей силой. В случае груза на пружине возвращающей силой является сила упругости, в случае математического маятника – составляющая силы тяжести.

Возвращающая сила по характеру подчиняется закону Гука F= -kx, где

– коэффициент возвращающей силы. Тогда потенциальная энергия колеблющейся точки равна:

(постоянную интегрирования выбирают равной нулю, чтобы при х=0 энергия Wn=0).

где , тогда

Полная механическая энергия равна сумме кинетической и потенциальной энергий, и в случае свободных колебаний без трения сохраняется (рис.1.1.15). Когда материальная точка совершает колебания, кинетическая энергия переходит в потенциальную, и наоборот. В крайних точках (х = ±А) скорость , кинетическая энергия равна нулю, и полная энергия равна потенциальной:

Таким образом, полная механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.

В положении равновесия (х=0) потенциальная энергия переходит в кинетическую:

В промежуточных точках полная энергия равна

а скорость

На рисунке 1.1.16 приведена кривая потенциальной энергии , горизонтальная линия соответствует полной энергии. Расстояние от этой линии до кривой равно кинетической энергии. Движение ограничено значениями х, заключёнными в пределах от –А до +А.

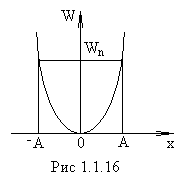
Средние за период значения кинетической и потенциальной энергии одинаковы и равны , так что средняя полная энергия системы равна полной энергии системы ( средние значения ).