Данная задача возникает при поиске частного решения дифференциального уравнения. Наш онлайн калькулятор, построенные на основе системы Wolfram Alpha, позволяет найти решение задачи Коши для различных типов дифференциальных уравнений. Чтобы начать работу, необходимо ввести данные своей задачи (дифференциальное уравнение и начальные условия) в калькулятор.
Найти решение задачи Коши для дифференциального уравнения:
при заданных начальных условиях:
При постановке задачи Коши, указываются так называемые начальные условия, позволяющие однозначно выделить искомое частное решение из общего. Эти условия включают в себя значения функции и всех её производных до включительно (где -порядок дифференциального уравнения), заданные в одной и той же точке .
Поясним вышесказанное на конкретном примере. Пусть нам требуется найти частное решение дифференциального уравнения:
удовлетворяющее начальным условиям:
Первым делом, используя различные методы (Бернули, вариации произвольной постоянной Лагранжа), сначала находим общее решение данного дифференциального уравнения:
Теперь, для поиска частного решения, нам необходимо использовать заданные начальные условия. Для этого, находим производную функции полученной ранее:
Далее, поставляем начальные условия в функцию и её производную :
Решая полученную систему уравнений получаем значения произвольных постоянных и :
Подставляем полученные результаты в общее решение дифференциального уравнения, в результате получаем искомое частное решение:
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
Другие полезные разделы:
Видео:19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать
Оставить свой комментарий:
Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме
Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать
Метод вариации произвольной постоянной решения линейных неоднородных уравнений
Пример №1 . Найдём общее решение уравнения y» + 4y’ + 3y = 9e -3 x . Рассмотрим соответствующее однородное уравнение y» + 4y’ + 3y = 0. Корни его характеристического уравнения r 2 + 4r + 3 = 0 равны -1 и -3. Поэтому фундаментальная система решений однородного уравнения состоит из функций y1 = e — x и y2 = e -3 x . Решение неоднородного уравнения ищем в виде y = C1(x)e — x + C2(x)e -3 x . Для нахождения производных C’1, C’2 составляем систему уравнений (8)
C′1·e -x +C′2·e -3x =0
-C′1·e -x -3C′2·e -3x =9e -3x
решая которую, находим 
, Интегрируя полученные функции, имеем 
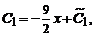
Окончательно получим
Пример №2 . Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:
y(0) =1 + 3ln3
y’(0) = 10ln3
Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 8 = 0
D = (-6) 2 — 4·1·8 = 4
Корни характеристического уравнения: r1 = 4, r2 = 2
Следовательно, фундаментальную систему решений составляют функции: y1=e 4x , y2=e 2x
Общее решение однородного уравнения имеет вид: y =C1·e 4x +C2·e 2x
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C’i составляем систему уравнений:
C′1·e 4x +C′2·e 2x =0
C′1(4e 4x ) + C′2(2e 2x ) = 4/(2+e -2x )
Выразим C’1 из первого уравнения:
C’1 = -c2e -2x
и подставим во второе. В итоге получаем:
C’1 = 2/(e 2x +2e 4x )
C’2 = -2e 2x /(e 2x +2e 4x )
Интегрируем полученные функции C’i:
C1 = 2ln(e -2x +2) — e -2x + C * 1
C2 = ln(2e 2x +1) – 2x+ C * 2
Поскольку y =C1·e 4x +C2·e 2x , то записываем полученные выражения в виде:
C1 = (2ln(e -2x +2) — e -2x + C * 1) e 4x = 2 e 4x ln(e -2x +2) — e 2x + C * 1 e 4x
C2 = (ln(2e 2x +1) – 2x+ C * 2)e 2x = e 2x ln(2e 2x +1) – 2x e 2x + C * 2 e 2x
Таким образом, общее решение дифференциального уравнения имеет вид:
y = 2 e 4x ln(e -2x +2) — e 2x + C * 1 e 4x + e 2x ln(2e 2x +1) – 2x e 2x + C * 2 e 2x
или
y = 2 e 4x ln(e -2x +2) — e 2x + e 2x ln(2e 2x +1) – 2x e 2x + C * 1 e 4x + C * 2 e 2x
Найдем частное решение при условии:
y(0) =1 + 3ln3
y’(0) = 10ln3
Подставляя x = 0, в найденное уравнение, получим:
y(0) = 2 ln(3) — 1 + ln(3) + C * 1 + C * 2 = 3 ln(3) — 1 + C * 1 + C * 2 = 1 + 3ln3
Находим первую производную от полученного общего решения:
y’ = 2e 2x (2C1 e 2x + C2 -2x +4 e 2x ln(e -2x +2)+ ln(2e 2x +1)-2)
Подставляя x = 0, получим:
y’(0) = 2(2C1 + C2 +4 ln(3)+ ln(3)-2) = 4C1 + 2C2 +10 ln(3) -4 = 10ln3
Получаем систему из двух уравнений:
3 ln(3) — 1 + C * 1 + C * 2 = 1 + 3ln3
4C1 + 2C2 +10 ln(3) -4 = 10ln3
или
C * 1 + C * 2 = 2
4C1 + 2C2 = 4
или
C * 1 + C * 2 = 2
2C1 + C2 = 2
Откуда: C1 = 0, C * 2 = 2
Частное решение запишется как:
y = 2e 4x ·ln(e -2x +2) — e 2x + e 2x ·ln(2e 2x +1) – 2x·e 2x + 2·e 2x
Видео:Видеоурок "Метод вариации произвольных постоянных"Скачать
Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
🎦 Видео
Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать
Курс по ОДУ: Метод вариации постоянных для решения линейных систем ДУ | Занятие 18Скачать
Асташова И. В. - Дифференциальные уравнения I - Метод вариации произвольных постоянныхСкачать
#Дифуры I. Урок 4. Линейные дифференциальные уравнения. Метод вариации произвольной постояннойСкачать
Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать
Закон БернуллиСкачать
Откуда появляются дифференциальные уравнения и как их решатьСкачать
Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать
10. ДУ. ЛНДУ 2 порядка. Метод вариации произвольных постоянных (2230 Минорский)Скачать
ЛНДУ. Метод вариации произвольных постоянных.Скачать
Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать
Решение системы дифференциальных уравнений методом ЭйлераСкачать
7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать
16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
