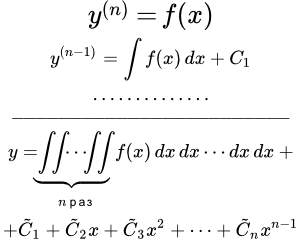Решение дифференциальных уравнений методом непосредственного интегрирования

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Общее решение

Рассмотрим дифференциальное уравнение n-го порядка, в котором n-я производная равна функции от независимой переменной x :
(1) .
Оно решается непосредственным интегрированием.
;
;

;
;

;
;
. . . . . . . .

.
Заменим постоянные интегрирования:
.
Тогда
(2) .
В результате мы получили общее решение (2) уравнения (1). Оно представляет собой сумму n-кратного повторного интеграла и многочлена степени .

Таким образом, если нас интересует общее решение уравнения (1), то мы должны проинтегрировать функцию n раз, и прибавить многочлен степени , коэффициентами которого являются постоянные интегрирования.

Видео:11. Уравнения в полных дифференциалахСкачать

Частное решение с заданными начальными условиями

Если нас интересует задача Коши с заданными начальными условиями
(3) ,
то соответствующее частное решение имеет следующий вид:
(4)
.
См. «Решение дифференциального уравнения y (n) =f(x) с заданными начальными условиями».

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Применение формулы Коши для повторных интегралов

Входящий в (4) n-кратный интеграл можно свести к однократному, если воспользоваться формулой Коши для повторных интегралов:
(5) .
Тогда решение уравнения (1) с начальными условиями (3) примет более простой вид:
(6)
.

Вывод формулы Коши (5) изложен на странице «Формула Коши для повторных интегралов». Здесь мы покажем, что функция , определяемое по формуле (6), удовлетворяет дифференциальному уравнению (1).

Выполняя n – 1 дифференцирований, получаем:
.
Дифференцируя еще раз, приходим к уравнению (1):
.

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Пример

Найти общее решение уравнения:
.

Разделим исходное уравнение на . При получаем уравнение вида (1):
.

Преобразуем постоянные интегрирования:
.

Автор: Олег Одинцов . Опубликовано: 16-07-2013 Изменено: 19-11-2020

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Метод непосредственного интегрирования

Метод интегрирования, при котором интеграл с помощью тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

Таким образом, алгоритм действий следующий:

1. тождественное преобразование подынтегральной функции;
2. применение свойств неопределенного интеграла: вынесение константы за знак интеграла, представление интеграла от суммы функций в вид суммы интегралов;
3. использование таблицы интегралов.

В простейших примерах для применения непосредственного интегрирования достаточно разложить подынтегральную функцию на слагаемые и постоянные величины вынести за знак интеграла.

При определенной практике интегрирования обычно эти действия проводят устно, записывая лишь результат интегрирования.

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Примеры решения интегралов данным методом

Задание. Найти интеграл $intleft(2 x^+frac+4^-frac<sqrt<1-x^>>right) d x$

Решение. Воспользуемся свойствами интеграла и приведем данный интеграл к нескольким табличным.

В некоторых случаях выражение, стоящее под знаком интеграла, можно с помощью алгебраических преобразований упростить так, чтобы можно было применить метод непосредственного интегрирования.

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Метод интегрирования дифференциального уравнения изгиба балки

Наиболее естественным методом определения функции прогибов является метод непосредственного интегрирования уравнения изгибающих моментов.

$EI,y»(x) = M(x)$ – полученное дифференциальное уравнение;

$EI,y'(x) = EI,varphi (x) = int dx + C$ – первый интеграл (уравнение углов поворота);

$EI,y(x) = int dx = iint dxdx + C,x + D$ – второй интеграл (уравнение прогибов).

Кроме интегрирования уравнения изгибающих моментов $M(x)$, для получения уравнения прогибов необходимо определить две постоянных интегрирования $C$ и $D$ из условий закрепления балки. При этом надо учесть, что шарнирная опора исключает прогибы балки, а жесткое зажатие – прогибы и углы поворота (то есть они равны нулю).

Физический смысл постоянных интегрирования такой: при $x = 0$ угол поворота $EI,varphi (0) = C$, а прогиб $EI,y(0) = D$, то есть константа $C$ равна углу поворота в начале координат, константа $D$ равна прогибу балки при x=0.

Видео:11 класс, 20 урок, Первообразная и неопределённый интегралСкачать

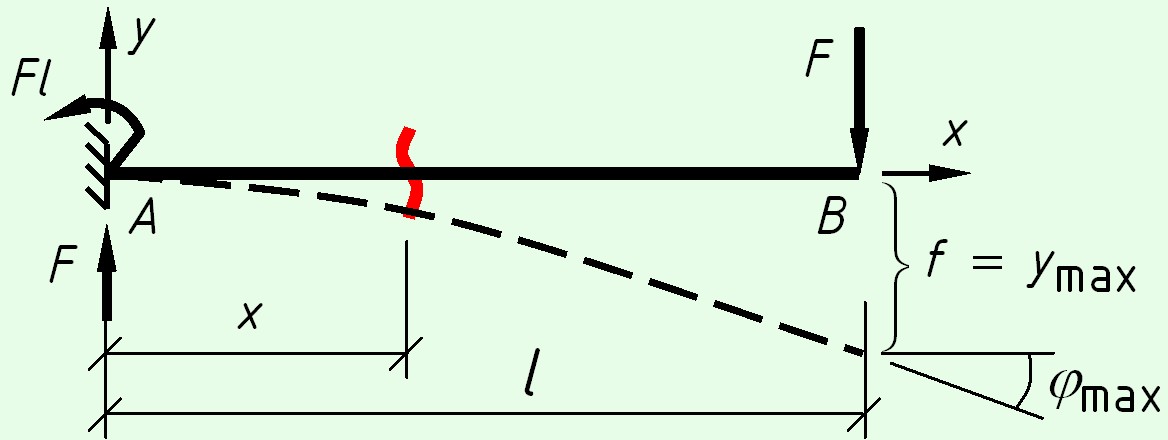
Консольная балка с силой на конце

На левой опоре возникают реакции – вертикальная сила $F$ и момент $M = F cdot l$.

Уравнения изгибающих моментов

$M(x) = — Fl + Fx = F(x — l)$

Уравнение углов поворота

$EI,y'(x) = EI,varphi (x) = int dx + C = F(frac<<>> — lx) + C$

Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений

$left < beginEI,varphi (0) = F(frac<<>> — l cdot 0) + C = 0 hfill \ EI,y(0) = F(frac<<>> — lfrac<<>>) + C cdot 0 + D = 0. hfill \ end right.$

Решение этой системы уравнений приводит к результату $C = 0$, $D = 0$.

Окончательно функция прогибов для рассматриваемой балки имеет вид

Максимальный прогиб будет иметь место при $x = l$

где знак « – » указывает направление перемещений – в сторону, противоположную положительному направлению оси $y$. Стрела прогиба $f = frac<<F,>><>$.

Максимальный угол поворота сечения также будет иметь место при $x = l$

знак « – » указывает направление угла поворота – сечение поворачивается по часовой стрелке.

Видео:Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

Шарнирно закрепленная балка с силой посередине

На опорах возникают вертикальные реакции $ = = F/2$.

Поскольку уравнение изгибающих моментов разное на двух разных участках, функция прогибов также будет разная. Используя полную симметрию расчетной схемы, далее будем рассматривать только левый участок, для которого уравнение изгибающих моментов имеет вид

$M(x) = fracx$, то есть $EI,y»(x) = fracx$, интегрируем дважды

Константы интегрирования $C$ и $D$ полученного уравнения справедливы только для первого участка, поэтому их необходимо определять из условий, связанных с перемещениями на первом участке. Такими условиями является равенство нулю прогибов на опоре $A$ ($x = 0$) и, исходя из симметрии, равенство нулю угла поворота под силой $F$ ($x = l/2$). Имеем систему уравнений

Окончательно функция прогибов для рассматриваемой балки имеет вид

Максимальный прогиб будет иметь место при $x = l/2$

Максимальные углы поворота сечений будут на опорах ($x = 0$ и $x = l$).

Видео:Математика без ху!ни. Интегралы, часть 1. Первообразная. Дифференцирование и интегрирование.Скачать

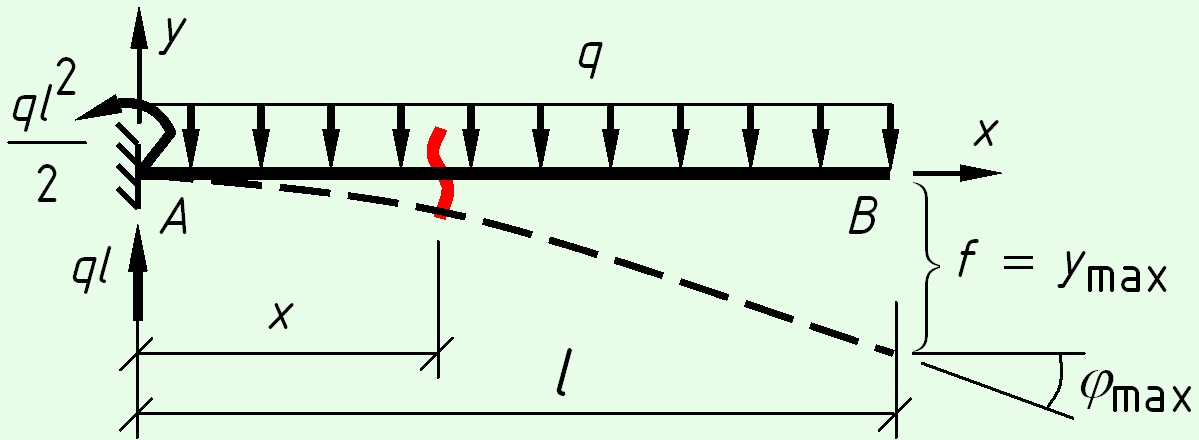
Консольная балка с равномерно распределенной нагрузкой

На левой опоре возникают реакции – вертикальная сила $ql$ и момент $M = frac<<q>>$.

$M(x) = — frac<<q>> + ql cdot x — frac<<q>>$, дважды интегрируем

Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений

$left < beginEI,y'(0) = F(frac<<>> — l cdot 0) + C = 0 hfill \ EI,y(0) = F(frac<<>> — lfrac<<>>) + C cdot 0 + D = 0. hfill \ end right.$

Решение системы уравнений приводит к результату $C = 0$, $D = 0$.

Окончательно функция прогибов для рассматриваемой балки имеет вид

Максимальный прогиб будет иметь место при $x = l$

Максимальный угол поворота сечения также будет иметь место при $x = l$

🌟 Видео

Дифференциальные уравнения, 9 урок, Линейные дифференциальные уравнения высших порядковСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

4.1 Метод интегрирования по частям. Часть 1Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

6. Особые решения ДУ первого порядкаСкачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Видеоурок "Системы дифференциальных уравнений"Скачать