Решение дифференциальных уравнений методом эйлера excel (4 видео)

Обзор методов решения в Excel

Введение

Уравнение называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области и, во всяком случае, зависит от . Его решением является любая функция u(x), которая этому уравнению удовлетворяет при всех x в определённом конечном или бесконечном интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид

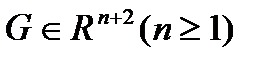
Решением этого уравнения на интервале I=[a,b] называется функция u(x).

Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х₀, х₁…, х_n и числа у₀, не определяя функцию у=F(x), найти такие значения у₁, у₂,…, у_n, что у_i=F(x_i)(i=1,2,…, n) и F(x₀)=y₀.

Таким образом, численные методы позволяют вместо нахождения функции y=F(x) (3) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k-x_k_-1 называется шагом интегрирования.

Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений – это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически симметричных полях и многое другое)

Обзор методов решения в Excel

1.1 Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка

Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов. Наиболее употребительным методом Рунге-Кутта решения уравнения первого порядка y’ = F(x,y) (1) является метод четвертого порядка, в котором вычисления производятся по формуле:

Видео:Решение ОДУ 1 го порядка в ExcelСкачать

Решение дифференциальных уравнений методом эйлера excel

Pers.narod.ru. Обучение. Excel: Решение обыкновенных дифференциальных уравнений (задача Коши)

Решение обыкновенных дифференциальных уравнений (ОДУ) — популярный раздел численных методов, немного теории можно почитать здесь.

В приведённом примере решается задача Коши, то есть, ищется решение дифференциального уравнения первого порядка вида dy/dx = f(x,y) на интервале x ∈ [x₀,x_n] при условии y(x₀)=y₀ и равномерном шаге сетки по x .

Решение выполняется методами Эйлера, «предиктор-корректор» (он же модифицированный метод Эйлера) и методом Рунге-Кутта 4 порядка точности. Пример может служить образцом для Ваших решений, правда, функцию придётся перепрограммировать несколько раз при различных значениях аргумента — поскольку без применения макросов на VBA Excel не позволяет создать полноценную функцию, которую было бы удобно вызывать с разными значениями аргументов.

Здесь решается уравнение dy/dx = 2x-y+x 2 на интервале [0,2] , начальное значение y(0)=0 , для оценки точности задано также точное решение в виде функции u(x)=x 2 . Оценка погрешности делается в норме L₁ , как и принято в данном случае.

Скачать пример в Excel XP/2003 (28 Кб)

Видео:Численное решение обыкновенных дифференциальных уравнений в ExcelСкачать

1.4 Численное решение уравнения методом Эйлера в Excel

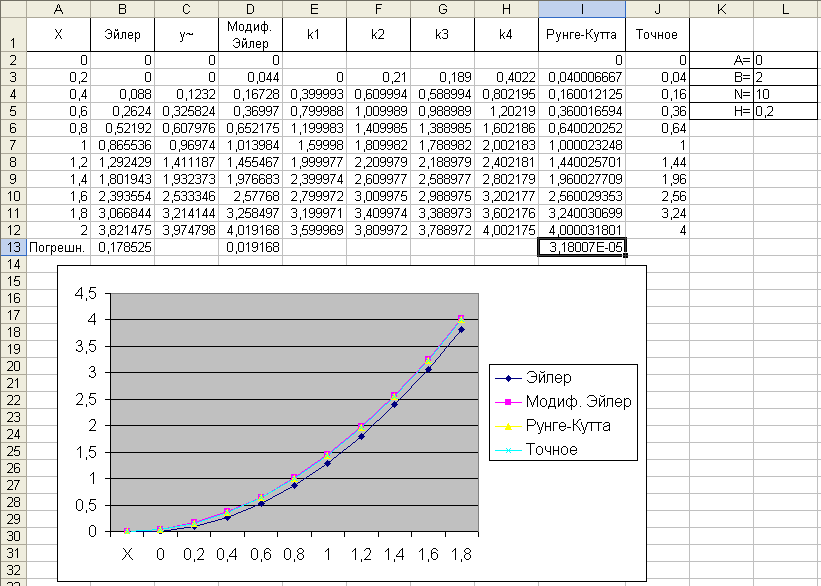
Рассмотрим расчетную таблицу в Excel, содержащую три столбца для значений . Дадим им заголовки x, y, , расположив их в ячейках A2:C2. Для постоянных величин h, c отведем отдельные ячейки E2 и E3. Их заголовки помещены в ячейки D2 и D3.

Расчеты в таблице Excel выполняются по следующему алгоритму:

1. Вычисление первого столбца: первые два значения x = x0 и x1 = x0+h вводятся в ячейки A3 и A4, затем, выделив две эти ячейки, заполняем столбец значений x до достижения конечного значения x=1,5.

2. Затем заполним первую строку расчетной таблицы: в столбце y введем y0 в ячейку B3, в столбце введем в ячейку C3 формулу: =$E$2*(A3^2-B3^2) (вычисляется приращение функции y для текущего значения x в соответствии с формулой ).

3. Вычисление второго столбца:

вводим формулу =В3+С3 в ячейку B4 и копируем ее в ячейки B5:B18 (вычисляется новое значение функции y при изменении x на один шаг с помощью линейного приращения по формуле ).

4. Вычисление третьего столбца:

копируем формулу из ячейки C3 в ячейки C4:C18

Рис. 1.1. Фрагмент рабочего листа с решением примера по методу Эйлера

2. ЧИСЛЕННОЕ РЕШЕНИЕ МЕТОДОМ РУНГЕ-КУТТА В EXCEL И TURBO PASCAL 7.0

2.1 Постановка задачи

Решить численно указанную задачу Коши для уравнения первого порядка методом Рунге-Кутта, используя табличный процессор Excel и с помощью программы на языке Турбо Паскаль 7.0. Построить графики решений в Excel, с помощью Мастера диаграмм. Провести анализ полученных результатов.

Исследовать поведение решения на отрезке [0,1.5] с начальным условием y(0)=0, числом отрезков разбиения n=15. Параметр c=0.2.

2.2 Математическая модель задачи (метод Рунге-Кутта).

Приводим уравнение к виду .

По условию выполнено соотношение: .

Расчетные формулы для конкретного примера записываются, исходя из общих формул: