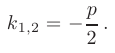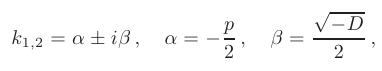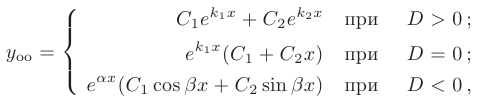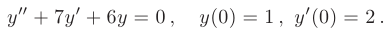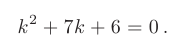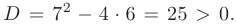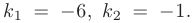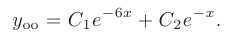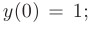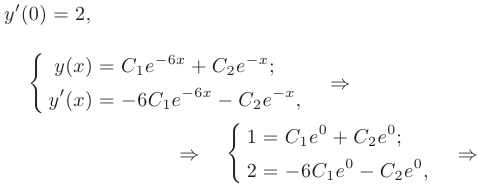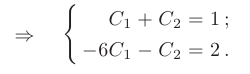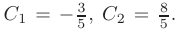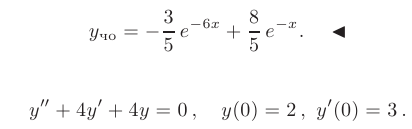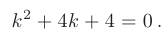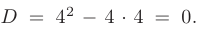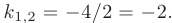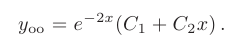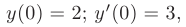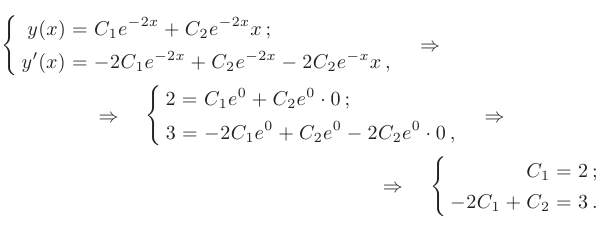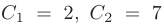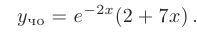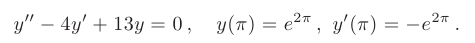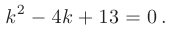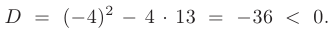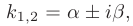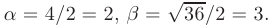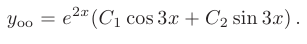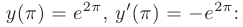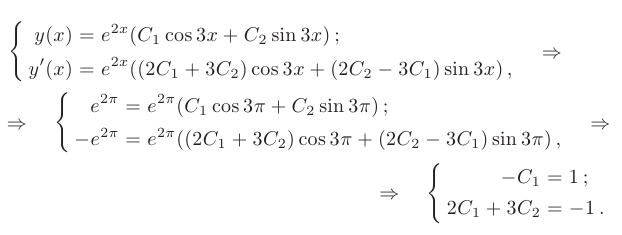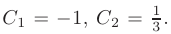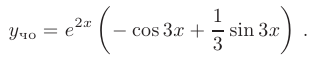Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами имеют вид
где p и q — действительные числа. Рассмотрим на примерах, как решаются однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Решение линейного однородного однородного дифференциального уравнения второго порядка зависит от корней характеристического уравнения. Характеристическое уравнение — это уравнение k²+pk+q=0.
1) Если корни характеристического уравнения — различные действительные числа:
то общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
2) Если корни характеристического уравнения — равные действительные числа
(например, при дискриминанте, равном нулю), то общее решение однородного дифференциального уравнения второго порядка есть
3) Если корни характеристического уравнения — комплексные числа
(например, при дискриминанте, равном отрицательному числу), то общее решение однородного дифференциального уравнения второго порядка записывается в виде
Примеры решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
Найти общие решения однородных дифференциальных уравнений второго порядка:
Составляем характеристическое уравнение: k²-7k+12=0. Его дискриминант D=b²-4ac=1>0, поэтому корни — различные действительные числа.
Отсюда, общее решение этого однородного ДУ 2-го порядка есть
Составим и решим характеристическое уравнение:
Корни действительные и различные. Отсюда имеем общее решение данного однородного дифференциального уравнения:
В этом случае характеристическое уравнение
Корни различны и действительны. Поэтому общее решение однородного дифференциального уравнения 2-го порядка здесь
Поскольку корни действительны и равны, для этого дифференциального уравнения общее решение записываем как
Характеристическое уравнение здесь
Так как дискриминант — отрицательное число, корни характеристического уравнения — комплексные числа.
Общее решение этого однородного дифференциального уравнения второго порядка имеет вид
Отсюда находим общее решение данного диф. уравнения:
Примеры для самопроверки.
Найти общее решение однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
Видео:Дифференциальные уравнения. 11 класс.Скачать

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
Видео:Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами в математике
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами
Рассмотрим метод решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами:
Линейной комбинацией функций 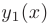
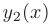
где 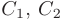
Функции 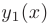
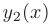
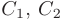
Теорема 7.2. Если 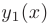
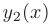
Следовательно, чтобы найти общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, надо знать два его частных линейно независимых решения: 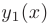
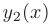
Будем искать частное решение дифференциального уравнения в виде 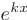
Очевидно, функция 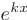
которое называется характеристическиль уравнением исходного дифференциального уравнения.
Как известно, для корней данного квадратного трехчлена возможны три случая.
- Если дискриминант больше нуля
, то корни характеристического уравнения действительные, простые:
- Если дискриминант равен нулю (
= 0), то корни характеристического уравнения действительные, кратные:
- Если дискриминант меньше нуля (
где 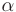
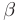
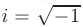
Теорема 7.3. Общее решение 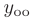
где 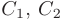
Пример:
Найти частные решения заданных линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами, удовлетворяющие начальным условиям:
► Составим характеристическое уравнение, заменяя в дифференциальном уравнении производные неизвестной функции у соответствующими степенями неизвестного 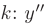
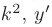
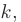
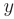
Дискриминант уравнения больше нуля:
В таком случае, корни характеристического уравнения действительные, простые:
Следовательно, общее решение дифференциального уравнения имеет вид
Частное решение получим из общего, используя для определения произвольных постоянных заданные начальные условия:
Решая полученную систему, находим значения произвольных постоянных:
После подстановки найденных значений в общее решение, искомое частное решение принимает вид
► Составим характеристическое уравнение:
Дискриминант уравнения равен нулю:
В таком случае, корни характеристического уравнения действительные, кратные:
Следовательно, общее решение дифференциального уравнения имеет вид
Найдем производную общего решения и определим произвольные постоянные из начальных условий:
Находим значения произвольных постоянных:
и подставим их в общее решение. Искомое частное решение принимает вид
Составим характеристическое уравнение:
Дискриминант меньше нуля:
В таком случае, корни характеристического уравнения комплексно-сопряженные:
Следовательно, общее решение дифференциального уравнения имеет вид
Используем для определения произвольных постоянных заданные начальные условия:
После подстановки найденных значений в общее решение, получим:
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
💥 Видео
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Однородное дифференциальное уравнениеСкачать

Дифференциальные уравнения для самых маленькихСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Частное решение дифференциального уравнения. 11 класс.Скачать

Решение дифференциальных уравнений ДИФФУРЫСкачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Решение однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

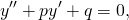
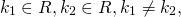
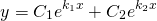
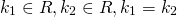
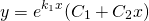
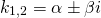
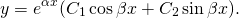
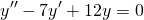
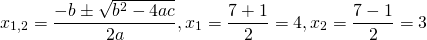
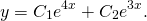
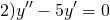
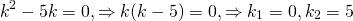
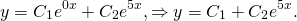
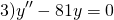
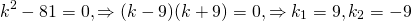
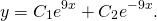
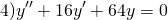
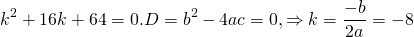
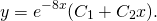
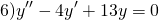
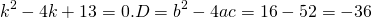
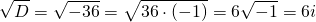
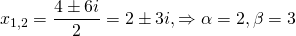
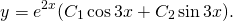
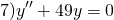
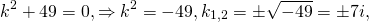
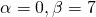
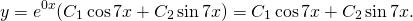

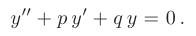
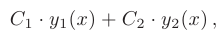
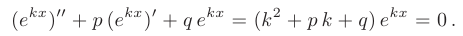
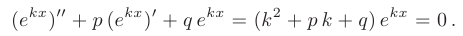
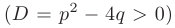 , то корни характеристического уравнения действительные, простые:
, то корни характеристического уравнения действительные, простые: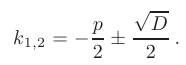
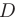 = 0), то корни характеристического уравнения действительные, кратные:
= 0), то корни характеристического уравнения действительные, кратные: