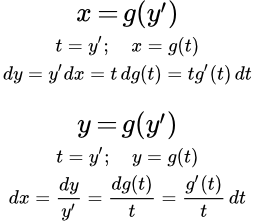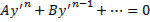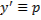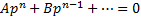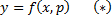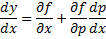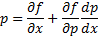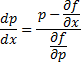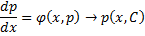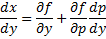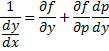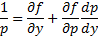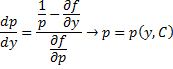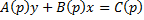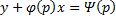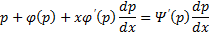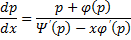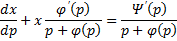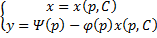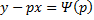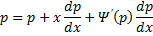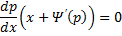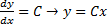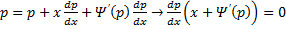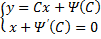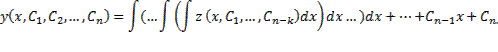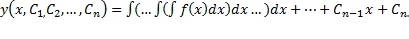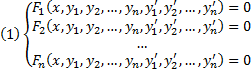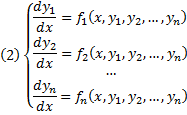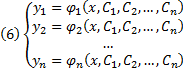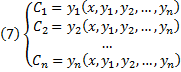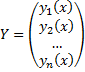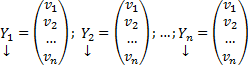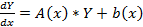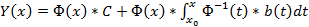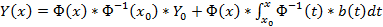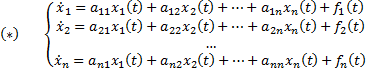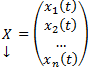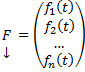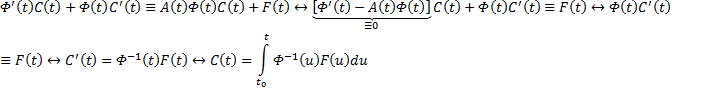Решение дифференциального уравнения в параметрическом виде

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Дифференциальные уравнения, не содержащие одну из переменных

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Постановка задачи

Здесь мы рассматриваем метод решения уравнений вида:
(1) ;
(2) .
То есть это дифференциальные уравнения первого порядка, не разрешенные относительно производной, и которые не содержат одну из переменных в явном виде.

Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Общий метод решения

Решение таких уравнений мы ищем в параметрическом виде. Пусть – параметр. Тогда переменные и являются функциями от этого параметра :
;
.
Производная также является функцией от параметра :
.

Преимущество параметрического представления заключается в том, что его можно создать многими способами. В качестве примера рассмотрим функцию
.
В параметрическом виде ее можно представить так:
.
Или так:
.
То есть мы можем найти бесконечно много способов, чтобы создать параметрическое представление для одной и той же функции.

Мы будем использовать это преимущество параметрического представления при решении уравнений (1) и (2). Общий метод заключается в том, чтобы подобрать такую функцию , чтобы уравнения (1) или (2) можно было разрешить относительно переменной или .

Рассмотрим уравнение (1):
(1) .
Пусть мы подобрали такую функцию , что при подстановке в (1), уравнение (1) удалось разрешить относительно . То есть мы получили параметрическое представление для переменной :
.
Тогда имея две функции и , мы можем найти . Для этого запишем дифференциал:
.
Интегрируя, получаем параметрическое представление для :
.

Теперь рассмотрим уравнение (2):
(2) .
Пусть мы подобрали такую функцию , что при подстановке в (2), уравнение (2) удалось разрешить относительно . То есть мы получили параметрическое представление для переменной :
.
Тогда имея две функции и , мы можем найти . Для этого запишем дифференциал:
.
Интегрируя, получаем параметрическое представление для :
.

Видео:14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Уравнения, разрешенные относительно переменной

Рассмотрим наиболее простой случай, когда исходное уравнение
(1)
удается разрешить относительно переменной :
.
В этом случае проще положить . Тогда .

Тогда имея две функции и , мы можем найти :
;
.

Аналогично, если исходное уравнение
(2)
удается разрешить относительно переменной :
.
То положим . Тогда .

Имея две функции и , мы можем найти :
;
.

Пример

Решить уравнение:
(1.1)

Это дифференциальное уравнение первого порядка, не разрешенное относительно производной. Оно не содержит переменную в явном виде. Ищем решение в параметрическом виде, введя параметр . Это уравнение разрешено относительно переменной . Поэтому делаем подстановку:
(1.2) .
Тогда
(1.3) .

Итак, мы выразили переменную через параметр . Теперь осталось выразить через параметр переменную . Для этого запишем дифференциал переменной :
.
Отсюда получаем дифференциал переменной :
(1.4) .
Распишем дифференциал , используя (1.3):
;
(1.5) .
Подставляем (1.2) и (1.5) в (1.4):
.
Интегрируем:
.

Итак, мы получили решение в параметрическом виде:
(1.6) ;
(1.3) .

Далее мы можем явно выразить y через x. Для этого перепишем уравнение (1.6):
.
Решаем квадратное уравнение:

.
Заменим постоянную :
:
.
Подставляем в (1.3):

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Уравнения, не разрешенные относительно переменной

Теперь рассмотрим более общий случай. Рассмотрим уравнение (1):
(1) .
Если это уравнение не удается разрешить относительно переменной , то у нас нет гарантий, что мы можем получить решение. Но мы можем попытаться найти такую функцию
, чтобы подставив в (1), можно было выразить переменную через параметр . Если это удастся сделать, то у нас будут две функции, зависящие от параметра :
;
.
Подставляя их в выражение для дифференциала

и интегрируя, мы найдем .

Аналогично поступаем для уравнения (2):
(2) .
Нашей задачей является найти такую функцию
, чтобы подставив в (2), можно было выразить переменную через параметр . Если это удастся сделать, то у нас будут две функции, зависящие от параметра :
;
.
Подставляя их в выражение для дифференциала

и интегрируя, мы найдем .

Пример

Решить уравнение:
(2.1) .

Это дифференциальное уравнение первого порядка, не разрешенное относительно производной. Оно не содержит переменную в явном виде. Ищем решение в параметрическом виде. Нашей задачей является найти такую подстановку , чтобы из уравнения (2.1) можно было выразить переменную через параметр .

Можно увидеть, что такой подстановкой является
(2.2) .
Подставляем в исходное уравнение (2.1):
;
;
;
(2.3) .

Итак, мы выразили переменную через параметр . Теперь осталось выразить через параметр переменную . Для этого запишем дифференциал переменной и выразим его через параметр .
.
Подставим (2.2):
.
Здесь – функция от , определяемая из (2.3).
Интегрируем по частям и подставляем (2.3):
;
;
.

Автор: Олег Одинцов . Опубликовано: 22-08-2012 Изменено: 01-04-2016

Видео:12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать

Дифференциальные уравнения 1-го порядка,
не разрешенные относительно производной

Видео:Видеоурок "Параметрические уравнения прямой"Скачать

Уравнения 1-го порядка n-ой степени относительно производной

Пусть имеем дифференциальное уравнение

Решаем это уравнение относительно . Пусть

— вещественные решения уравнения (1).

Общий интеграл уравнения (1) выразится совокупностью интегралов:

где есть интеграл уравнения .

Таким образом, через каждую точку области, в которой принимает вещественные значения, проходит интегральных линий.

Пример 1. Решить уравнение .

Решение. Разрешим это уравнение относительно :

Пример 2. Решить уравнение .

Решение. Разрешим уравнение относительно переменной :

Положим , где — параметр; тогда получим Дифференцируя, найдем . Но так как , то будем иметь

Рассмотрим два случая:

1) , откуда , где — произвольная постоянная. Подставляя значение , получаем общее решение данного уравнения:

В равенстве нельзя заменить на и интегрировать полученное уравнение (так как при этом появится вторая произвольная постоянная, чего не может быть, поскольку рассматриваемое дифференциальное уравнение является уравнением первого порядка).

2) , откуда . Подставляя, получим еще одно решение .

Проверим, нарушится ли свойство единственности в каждой точке решения , т.е. является ли оно особым (см. часть 1.11). Для этого возьмем на интегральной кривой произвольную точку , где . Будем теперь искать решение, которое содержится в общем решении и график которого проходит через точку . Подставляя координаты этой точки в общее решение , будем иметь

откуда . Это значение постоянной подставим в . Тогда получим частное решение

которое не совпадает с решением . Для этих решений имеем соответственно . При обе производные совпадают. Следовательно, в точке нарушается свойство единственности, т. е. через эту точку проходят две интегральные кривые с одной и той же касательной. Так как произвольно, то единственность нарушается в каждой точке решения , а это означает, что оно является особым.

Видео:Параметрические уравнения прямойСкачать

2°. Уравнения вида f(y,y’)=0 и f(x,y’)=0

Если уравнения и легко разрешимы относительно , то, разрешая их, получим уравнения с разделяющимися переменными. Рассмотрим случаи, когда эти уравнения не разрешимы относительно .

А. Уравнение вида разрешимо относительно :

Полагаем , тогда . Дифференцируя это уравнение и заменяя на , получим

Получаем общее решение уравнения в параметрической форме

Пример 3. Решить уравнение , где — постоянные.

Решение. Положим , тогда , или . Отсюда и .

Общим решением будет .

Б. Если уравнение вида неразрешимо (или трудно разрешимо) как относительно , так и относительно , но допускает выражение и через некоторый параметр :

то поступаем следующим образом. Имеем . С другой стороны, , так что и ; отсюда

Таким образом, получаем общее решение данного дифференциального уравнения в параметрической форме

Пример 4. Решить уравнение .

Решение. Полагаем , тогда имеем

Отсюда , общее решение .

В. Уравнение вида . Пусть это уравнение разрешимо относительно , то есть .

Полагая , получим . Но и, следовательно, , так что

Таким образом — общее решение уравнения в параметрической форме ( — параметр).

Замечание. В формулах нельзя рассматривать как производную. В них является просто параметром.

Пример 5. Решить уравнение .

Решение. Положим , тогда

Итак, — общее решение.

Аналогично случаю Б можно пытаться решать уравнение методом введения параметра .

Видео:ПАРАМЕТРИЧЕСКИЙ метод решения диффуров ОБОШЕЛ избранниц холостяка | Дифференциальные уравненияСкачать

3°. Уравнения Лагранжа

Уравнение Лагранжа имеет вид

Полагая , дифференцируя по и заменяя на , приводим это уравнение к линейному относительно как функции . Находя решение этого последнего уравнения , получаем общее решение исходного уравнения в параметрической форме:

Кроме того, уравнение Лагранжа может иметь еще особые решения вида , где — корень уравнения .

Пример 6. Проинтегрировать уравнение .

Решение. Полагаем , тогда . Дифференцируя, находим

Получили уравнение первого порядка, линейное относительно ; решая его, находим

Подставляя найденное значение в выражение для , получим окончательно

Видео:11. Уравнения в полных дифференциалахСкачать

Уравнения Клеро

Уравнение Клеро имеет вид .

Метод решения тот же, что и для уравнения Лагранжа. Общее решение уравнения Клеро имеет вид

Уравнение Клеро может иметь еще особое решение, которое получается исключением из уравнений .

Пример 7. Проинтегрировать уравнение .

Решение. Полагая , получаем . Дифференцируя последнее уравнение и заменяя на , найдем

Приравнивая нулю первый множитель, получаем , откуда и общее решение исходного уравнения есть , однопараметрическое семейство прямых. Приравнивая нулю второй множитель, будем иметь . Исключая из этого уравнения и из уравнения , получим — это тоже решение нашего уравнения (особое решение).

С геометрической точки зрения кривая есть огибающая семейства прямых, даваемых общим решением (рис. 14).

Видео:Курс по ОДУ: Уравнения Клеро и Лагранжа | Занятие 8Скачать

Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.

Уравнения, не разрешённые относительно производной, выглядят так: .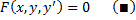

Уравнения первого порядка n-ой степени решаются так:

Если из уравнения y можно выразить, то есть , то это решается методом введения параметра, а именно: Обозначим , получим:

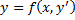
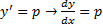
Продифференцируем по x:

Получили уравнение, разрешённое относительно производной. p(x,C) подставляем в (*), получим: 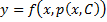. Это и будет решение.

Рассмотрим теперь случай, когда из уравнения можно явно выразить x, то есть . Вводим параметр , получаем . Дифференцируем по y обе части:

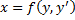
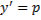
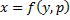
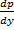
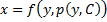
Мы получили уравнение, разрешённое относительно производной . В итоге получаем: .

Уравнение Лагранжа – это уравнение, линейное относительно x и y, оно имеет вид: 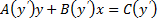. Уравнения Лагранжа ВСЕГДА интегрируется в квадратурах.

Принцип решения: Вводим параметр 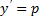, получаем:

Пусть 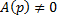, поделим всё выражение на A(p):

Продифференцируем по x:

Получили линейное уравнение первого порядка. Отсюда находим .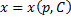

В итоге решение в параметрическом виде:

Отдельно рассмотрим случай, когда :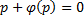

Если это тождество, то есть 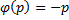, то:

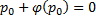
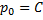
Если это не тождество, а уравнение с корнями: например, p0 – корень, то есть , тогда – решение.

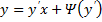
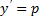
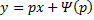
Частный случай уравнения Лагранжа – это уравнение Клеро. Это когда уравнение Лагранжа имеет следующий вид: . Принцип решения: Вводим параметр , получаем . Дифференцируем по x, получаем:

Общее решение уравнения Клеро:

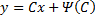
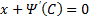
Здесь – семейство всевозможных кривых; – огибающая этого семейства, тоже является решением и называется особое решение.

Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (ФСР) однородного уравнения, общее решение неоднородного уравнения.

Простейшие ОДУ высших порядков, интегрируемые в квадратурах и допускающие понижение порядка.

Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида F (x, y(x), y ‘(x), y »(x), … , y(n)(x)) = 0, где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число n называется порядком уравнения.

Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a, b), если она n раз дифференцируема на (a, b) и при подстановке в уравнение обращает его в тождество. Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, называют уравнениями в нормальной форме: y(n) = f(x, y, y ‘, y », … , y(n − 1)).

Дифференциальное уравнение обычно имеет бесконечно много решений. Чтобы выделить нужное решение, используют дополнительные условия. Чтобы выделить единственное решение уравнения n–го порядка обычно задают n начальных условий y(x0) = y0, y ‘(x0) = y1, y »(x0) = y2, … , y(n − 1)(x0) = yn − 1.

Общим решением дифференциального уравнения F(x, y(x), y ‘(x), y »(x), … , y(n )(x)) = 0 называется функция y = Ф(x, С1, С2, … , Сn), содержащая некоторые постоянные (параметры) С1, С2, … , Сn, и обладающая следующими свойствами:

Ф(x, С1, С2, … , Сn) является решением уравнения при любых допустимых значениях С1, С2, … , Сm;

для любых начальных данных y(x0) = y0, y ‘(x0) = y1, y »(x0) = y2, … , y(n − 1)(x0) = yn − 1, для которых задача Коши имеет единственное решение, существуют значения постоянных С1 = A1, С2 = A2, … , Сn = An, такие что решение y = Ф(x, A1, A2, …, An) удовлетворяет заданным начальным условиям.

Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С1, С2, . Сn) = 0.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.

Если задачу об отыскании всех решений дифференциального уравнения удается свести к алгебраическим операциям и к вычислению конечного числа интегралов и производных от известных функций, то уравнение называется интегрируемым в квадратурах. Класс таких уравнений относительно узок.

Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ‘. y(n) ) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка.

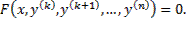
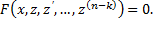
К уравнениям, допускающим понижение порядка, относятся в частности, уравнения, не содержащие искомой функции и ее производных до некоторого порядка, , т.е. уравнения вида Заменой z(x) = y(k)(x) такое уравнение сводится к уравнению (n−k)–го порядка: Если z = z(x,C1. Cn-k) решение этого уравнения, то общее решение уравнения n–го порядка может быть вычислено по формуле

Простейшее уравнение, допускающее понижение порядка — уравнение вида y(n) = f (x), его общее решение имеет вид

К уравнениям, допускающим понижение порядка, относятся уравнения, не содержащие независимой переменной — уравнения вида F(y, y’, . y(n)) = 0. Порядок уравнения можно понизить заменив y ‘ = p(y). После подстановки получим дифференциальное уравнение относительно функции p = p(y) , в котором порядок старшей производной от p(y) будет на единицу меньше, чем порядок старшей производной от y(x) в исходном уравнении.

К уравнениям, допускающим понижение порядка, относятся уравнения, не содержащие искомой функции — уравнения вида F(x, y’, . y(n)) = 0. Порядок уравнения можно понизить заменив y ‘ = p(x). После подстановки получим дифференциальное уравнение относительно функции p = p(x) на единицу меньшего порядка, чем исходное уравнение: F(x, p, p’, . p(n — 1)) = 0. Если правая часть уравнения F(x, y, y ‘. y(n) ) = 0, удовлетворяет условию однородностиF(x, ty, ty ‘. ty(n) ) = tk F(x, y, y ‘. y(n) ) то говорят, что это уравнение, однородное относительно неизвестной функции и всех ее производных. Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ‘. y(n) ) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка.

К уравнениям, допускающим понижение порядка, относятся уравнения, однородные относительно неизвестной функции и всех ее производных. Порядок такого уравнения можно понизить заменой

Выражение для первой производной от y(x) не содержит производной от z(x):

.

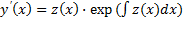
Поэтому, заменив в исходном уравнении y, y ‘. y(n) их выражениями через z(x), получим относительно z(x) дифференциальное уравнение на единицу меньшего порядка.

Основные понятия, относящиеся к системам ОДУ: порядок системы, нормальная форма системы, общее и частное решения, общий и первый интегралы. Задача Коши для нормальной системы, её геометрический смысл.

Совокупность соотношений вида:

Где y1, y2, …, yn искомые функции от независимой переменной x, называется системой обыкновенных дифференциальных уравнений первого порядка.

Будем предполагать функции F2, F2, …, Fn такими, что система разрешима относительно производных от искомых функций:

Такие системы называются нормальными системами дифференциальных уравнений.

Число уравнений, входящих в систему, называется порядком этой системы. Значит, наша система имеет n-ый порядок.

Такая система, когда в левой части уравнений стоят производные первого порядка, а правые части не содержат производных, называется нормальной.

Семейство решений системы (2), зависящее от n произвольных постоянных C1, C2, …, Cn

называют обычно общим решением этой системы.

Дадим определение общего решения системы (2) в области D изменения переменных x, y1, y2, …, yn.

В качестве области D будем рассматривать область в пространстве (x, y1, y2, …, yn), в каждой точке которой имеет место существование и единственность решения задачи Коши для системы (2).

Совокупность n функций (6), определённых в некоторой области изменения переменных x, C1, C2, …, Cn, имеющих непрерывные частные производные по x, будем называть общим решением системы (2) в области D, если система (6) разрешима относительно произвольных постоянных C1, C2, …, Cn в области D, так что при любых значениях x, y1, y2, …, yn, принадлежащих области D, системой (6) определяются значения C1, C2, …, Cn:

и если совокупность n функций (6) является решением системы (2) при всех значениях произвольных постоянных C1, C2, …, Cn, доставляемых формулами (7), когда точка (x, y1, y2, …, yn) пробегает область D.

Решение, получающееся из формулы общего решения при частных числовых значениях произвольных постоянных C1, C2, …, Cn,, включая бесконечности, будет частным решением.

Решая задачу Коши при помощи формулы общего решения всегда получаем частное решение.

1-ое определение интеграла системы. Функция φ(x, y1, y2, …, yn), не приводящаяся к постоянной, называется интегралом системы (2), если при замене y1, …, yn любым частным решением этой системы она обращается в постоянную.

2-ое определение интеграла системы. Функция φ(x, y1, y2, …, yn), имеющая непрерывные частные производные по x, y2, …, yn, и такая, что в рассматриваемой области 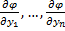не обращаются одновременно в нуль, называется интегралом системы (2), если полный дифференциал этой функции обращается тождественно в нуль в силу системы (2), то есть имеет место тождество:

.

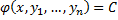
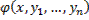
Равенство , где – интеграл системы (2) в смысле первого или второго определения, а C – произвольная постоянная, называется первым интегралом системы (2). Например, каждое из равенств (7) является первым интегралом системы (2).

Совокупность n первых интегралов (7) обладает тем свойством, что она разрешима относительно искомых функций y1, y2, …, yn, причём в результате этого мы получаем общее решение (6) системы (2) в области D. Всякую совокупность n первых интегралов, обладающую таким свойством, будем называть общим интегралом системы (2) в области D.

Фундаментальные системы решений нормальной системы однородных линейных ОДУ. Теорема существования фундаментальных систем. Теорема об общем решении (о структуре общего решения) нормальной системы однородных линейных ОДУ.

Система обыкновенных дифференциальных уравнений вида:

называется линейной системой. При система становится однородной. В векторно-матричной форме: , где
,

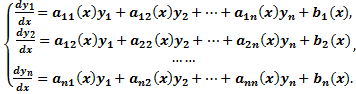
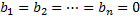
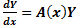
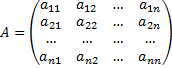
Будем искать решение . Ищем решение системы в таком виде:

Фундаментальной системой решений системы уравнений (*) называется системы из n линейно независимых вектор-функций.

Теорема о структуре общего решения линейного однородного дифференциального уравнения. Общее решение y(x) линейного однородного дифференциального уравнения есть линейная комбинация функций из фундаментальной системы решений этого уравнения: .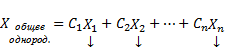

Теорема об общем решении (о структуре общего решения) нормальной системы неоднородных линейных ОДУ.

Рассмотрим неоднородную линейную систему обыкновенных дифференциальных уравнений n-го порядка

Здесь A

Справедлива следующая теорема о структуре общего решения этой неоднородной линейной системы ОДУ.

Если матрица A(x) и вектор-функция b(x) непрерывны на [a, b], и пусть Φ(x) — фундаментальная матрица решений однородной линейной системы 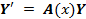, то общее решение неоднородной системы Y’ = A(x)Y + b(x) имеет вид:

где C — произвольный постоянный вектор-столбец, x0 — произвольная фиксированная точка из отрезка [a, b].

Из приведенной формулы легко получить формулу решения задачи Коши для линейной неоднородной системы ОДУ — формулу Коши.

Решением задачи Коши 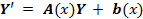, Y(x0) = Y0 является вектор-функция

Метод вариации произвольных постоянных для отыскания частных решений нормальной системы неоднородных линейных ОДУ.

Определение системы неоднородных линейных ОДУ. Система ОДУ вида:

называется линейной неоднородной. Пусть

Система (*) в векторно-матричном виде: . — система однородная, иначе – неоднородная.

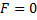
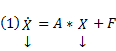
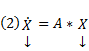
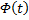
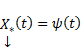
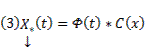
Сам метод. Пусть имеется линейная неоднородная система , тогда — линейная однородная система, соответствующая линейной неоднородной. Пусть – фундаментальная матрица системы решений, , где C – произвольный постоянный вектор, — общее решение системы. Станем искать решение системы (1) в виде , где C(x) – неизвестная (пока) вектор-функция. Хотим, чтобы вектор-функция (3) была решением системы (1). Тогда должно быть справедливо тождество:

(произвольный постоянный вектор, который получается в результате интегрирования, можно считать равным 0). Здесь точки x0, – любые.

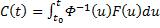
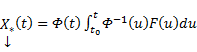
Видим, таким образом, что если в (3) в качестве C(t) брать , то вектор-функция будет решением системы (1).

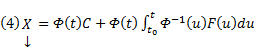
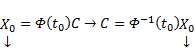
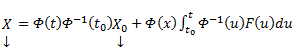
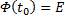
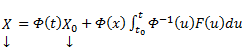
Общее решение линейной неоднородной системы (1) может быть записано в виде . Пусть требуется найти решение системы (1), удовлетворяющее начальному условию . Подстановка (4) начальных данных (5) даёт . Следовательно, решение задачи Коши (1)-(5) может быть записано в виде: . В частном случае, когда , последняя формула принимает вид: .

🔍 Видео

13. Как решить дифференциальное уравнение первого порядка?Скачать

301 Нахождение решения дифференци ального уравнения в виде степенного рядаСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать