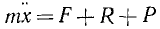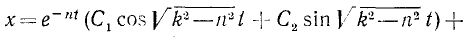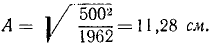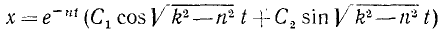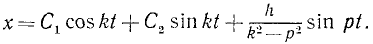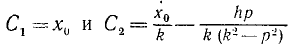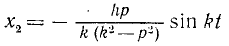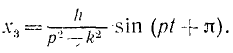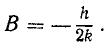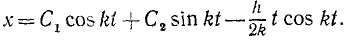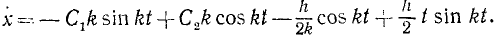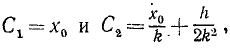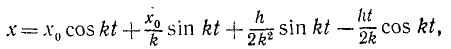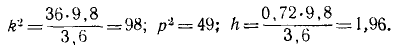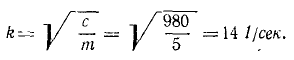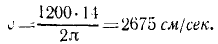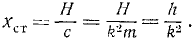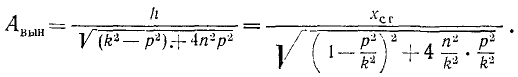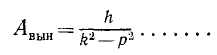Решение дифференциального уравнения собственных колебаний материальной точки имеет вид

Глава 13. Динамика точки.

13.5. Свободные затухающие колебания.

13.5.1. Решение дифференциального уравнения затухающих колебаний материальной точки имеет вид x = е -0,2t (С₁ cos3t + C₂ sin3t). Опре­делить постоянную интегрирования С₁, если в момент времени t_o = 0 координата точки х₀ = 0,2 м. (Ответ 0,2)

13.5.2. Решение дифференциального уравнения затухающих колебаний материальной точки имеет вид х = е -0,5t (С₁ cos 3t + С₂ sin 3t). Опре­делить постоянную интегрирования С₂, если постоянная интегрирова­ния C₁ = 1,5 и в момент времени t₀ = 0 скорость точки v₀ = 0. (Ответ 0,25)

13.5.3. Дифференциальное уравнение движения материальной точки имеет вид mх + 4х + 2х = 0. Найти максимальное значение массы точ­ки, при котором движение будет апериодическим. (Ответ 2)

13.5.4. Груз подвешен к пружине с коэффициентом жесткости с = 200 Н/м и движется по прямой согласно уравнению y = Ae -0,9t sin(5t + а). Определить массу груза. (Ответ 7,75)

13.5.5. На материальную точку массой m = 6 кг, которая находится в колебательном движении, действует сила сопротивления R = —μv. Определить коэффициент если закон движения точки имеет вид х = Ae -0,1t sin(7t + а) (Ответ 1,2)

13.5.6. Груз массой m = 2 кг прикреплен к пружине, коэффициент жест­кости которой с = 30 Н/м, и выведен из состояния равновесия. Опре­делить, находится ли точка в колебательном движении, если сила сопротивления движению R = — 0,1v. (Ответ Да)

13.5.7. Дифференциальное уравнение движения материальной точки имеет вид 2х + 2х + 50х = 0. Найти минимальное значение коэффици­ента μ сопротивления среды, при котором движение будет апериодическим. (Ответ 20)

13.5.8. Определить, находится ли материальная точка в колебательном движении, если дифференциальное уравнение движения имеет вид х +2x + 2х = 0. (Ответ Да)

13.5.9. Дифференциальное уравнение движения материальной точки имеет вид 3х + 12х + сх = 0. Найти максимальное значение коэф­фициента жесткости с, при котором движение будет апериодичес­ким. (12)

13.5.10. Определить, находится ли материальная точка в колебательном движении, если дифференциальное уравнение движения имеет вид х + 5х + 5х = 0. (Ответ Нет)

13.5.11. На материальную точку массой m = 10 кг, которая находится в колебательном движении, действует сила сопротивления R = —μv. Определить коэффициент μ, если период затухающих колебаний T₁ = 2 с, а отношение последующего максимального отклонения точки к предыдущему в ту же сторону равно 0,85. (Ответ 1,63)

13.5.12. Дифференциальное уравнение движения материальной точки име­ет вид 3х + μx + 48х = 0. Найти наименьшее значение коэффициента μ сопротивления среды, при котором движение системы будет апериодическим. (Ответ 24)

13.5.13. Решение дифференциального уравнения затухающих колебаний тела имеет вид х = Ае -0,8t sin(4t + а). Определить коэффициент жест­кости пружины, к которой прикреплено тело, если его масса m = 10 кг. (Ответ 166)

13.5.14. Дифференциальное уравнение движения материальной точки имеет вид 5х + 20х + сх = 0. Найти наибольшее значение коэф­фициента жесткости с, при котором движение точки будет апериодическим. (Ответ 20)

13.5.15. Затухающие колебания материальной точки описываются уравне­нием х = Аe -0,2t sin(0,5t + а). Определить угловую частоту свободных колебаний этой точки в случае, если силы сопротивления отсутствуют (Ответ 0,539)

13.5.16. Дифференциальное уравнение колебательного движения мате­риальной точки имеет вид х + 8х + 25х = 0. Найти угловую частоту затухающих колебаний. (Ответ 3)

13.5.17. Груз массой m = 2 кг подвешен к пружине с коэффициентом жесткости с = 30 Н/м и находится в колебательном движении. Опре­делить угловую частоту затухающих колебаний, если сила сопротивления движению груза R = 4v. (Ответ 3,74)

13.5.18. Уравнение движения материальной точки имеет вид х = е -0.05t (0,3 cos4t + 0,5 sin4t). Для того чтобы выразить уравнение движе­ния в виде х = А е -nt sin (k₁t + а), определить величину А. (Ответ 0,583)

13.5.19. Дифференциальное уравнение колебательного движения матери­альной точки имеет вид х + 6х + 50х = 0. Определить период затуха­ющих колебаний. (Ответ 0,981)

13.5.20. Дифференциальное уравнение колебательного движения матери­альной точки имеет вид х + 8х + 25х = 0. Найти период затухающих колебаний. (Ответ 2,09)

13.5.21. Колебательное движение материальной точки задано уравнением x = 0,7e -0,4t sin(1,5t +0,6). Определить период свободных колебаний точки в том случае, когда силы сопротивления отсутствуют.
(Ответ 4,05)

13.5.22. Колебательное движение материальной точки описывается урав­нением у = 6e -0,3t sin(8t + 0,3) Определить период затухающих колебаний точки. (Ответ 0,785)

13.5.23. Дифференциальное уравнение затухающих колебаний имеет вид х + 0,6x + 16х = 0. Определить отношение последующего максималь­ного отклонения точки к предыдущему в ту же сторону. (Ответ 0,624)

13.5.24. Затухающие колебания материальной точки описываются урав­нением х = 0,12е -0,1t sin(18t + 0,2). Определить отношение последу­ющего максимального отклонения точки к предыдущему в ту же сторону. (Ответ 0,966)

13.5.25. Дифференциальное уравнение колебательного движения матери­альной точки имеет вид х + 4х + 20х = 0. Найти логарифмический декремент колебаний, рассматривая максимальные отклонения после полупериода колебаний. (Ответ 1,57)

Сборник коротких задач по теоретической механике.
Кепе О.Э.

Книга состоит из 1757 заданий которые предназначены для бысторого
контроля знаний на занятиях и зачетах а также для допуска к экзамену.
Задачи имеют ответы.

Издательство «Высшая школа» 1989 Москва

Также решение задач Кепе можно скачать здесь:
Мобильное приложение для Андроид:

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

ФИЗИКА КОЛЕБАНИЙ И ВОЛН

Видео:Свободные колебания материальной точки 2Скачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СОБСТВЕННЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ МАТЕРИАЛЬНОЙ ТОЧКИ

Движения и циклические процессы, характеризуемые определенной повторяемостью во времени, называют колебаниями. Они чрезвычайно распространены в природе и технике. Это суточные и годичные изменения температуры, морские приливы и отливы, волны на поверхности морей и океанов, разрушительные колебания коры планеты, биение сердца, дыхательный ритм, вибрации механизмов и сооружений (амплитуда колебаний вершины Останкинской телебашни при сильном ветре достигает 2,5 м), движение поршней двигателей внутреннего сгорания, акустические процессы, тепловое движение ионов и атомов кристаллической решетки твердого тела и движение электронов в атоме, переменный ток и его электромагнитное поле. В ряде случаев колебания играют отрицательную роль. Это колебания (вибрации) крыльев самолета; моста, возникающие из-за толчков на стыках рельс, при прохождении поезда; корпуса корабля, вызванные вращением гребного винта, и т.п. Все эти процессы могут привести к катастрофическим последствиям. В подобных случаях необходимо воспрепятствовать тому, чтобы колебания достигли опасных размеров. Вместе с тем колебательные процессы составляют основу некоторых технических устройств и даже отраслей техники. Так, радиотехника основана на колебательных процессах.

В зависимости от характера воздействия, вызывающего и поддерживающего колебательный процесс, колебания классифицируют на свободные (или собственные), вынужденные, автоколебания и параметрические.

Свободные, или собственные, колебания происходят в системе, предоставленной самой себе, после того как ей был сообщен толчок или она была выведена из положения равновесия. Примером собственных колебаний является движение подвешенного на нити шарика.

Вынужденные колебания появляются в системе от воздействия внешней периодически изменяющейся силы. Примером вынужденных колебаний может служить колебание моста, возникающее при прохождении по нему шагающих в ногу людей.

Автоколебания, как и вынужденные колебания, сопровождаются воздействием на систему внешних сил, но при этом система сама управляет внешним воздействием. Примером автоколебательной системы являются часы. В них маятник получает толчки за счет энергии поднятой гири или упругой пружины. Однако толчки имеют место в те моменты времени, когда маятник проходит через среднее положение.

Параметрические колебания в системе происходят также от внешнего воздействия при периодическом изменении одного из параметров системы. Примером параметрических колебаний является движение шарика, подвешенного на нити переменной длины.

Физическая природа колебаний может быть разной, и поэтому колебательные системы принято классифицировать на механические, электрические, информационные, биологические и др. Особое значение имеют колебания двух видов: механические и электромагнитные. К механическим относят колебания маятников, струн, вибрации различных механизмов и сооружений, а также акустические колебания, волны на поверхности водоемов и др., к электромагнитным — колебания тока в электрической цепи, колебания напряженности электрического и магнитного полей в электромагнитной волне. По форме колебания могут быть разделены на прямоугольные, треугольные и синусоидальные (рис. 13.1).

Опыт указывает на многообразие форм колебательного движения и на то, что анализ их осуществляется единым методом. Простейшими являются гармонические колебания, при которых колеблющаяся величина изменяется со временем по закону косинуса — синуса. Большая часть реальных колебаний близка к гармоническим, и в ряде случаев подобные колебания идеализируются и считаются гармоническими. Важным является и то обстоятельство, что периодические процессы иной негармонической формы могут быть представлены как наложение нескольких гармонических колебаний. Теория гармонических колебаний используется буквально во всех разделах физики: в теории упругости, акустике, оптике, электричестве и электромагнетизме, учении об атоме и др.

Одним из методов графического изображения гармонического колебания является метод вращающегося вектора амплитуды (рис. 13.2), называемый также методом векторных диаграмм. Для этого из точки О, взятой на оси х, под углом ф откладывается вектор А, модуль которого равен амплитуде А рассматриваемого колебания. Пусть вектор А движется против часовой стрелки с угловой скоростью со = const. Проекция конца вектора на ось х или s будет перемещаться вдоль оси и принимать значения от +А до —А. Отклонение колеблющейся величины х со временем определяется соотношением х = /4cos9, а применительно к оси s: s = .dsirnp. На этом же рисунке дано графическое построение синусоиды. Итак, гармоническое колебание может быть представлено проекцией вектора амплитуды А на произвольно выбранную ось. Именно такое изображение гармонического колебательного процесса воспроизводится регистрирующими приборами, в том числе используемыми в системах управления воздушным движением.

Колебания представляют собой движение с переменным ускорением. Отклонение, скорость и ускорение являются функциями времени.

Для гармонического, например, движения системы по окружности, описываемого уравнением типа s = ^coscp = y4cos(cof + cp₀), первая производная по времени представляет собой мгновенную скорость колеблющейся системы:

Мгновенное ускорение колебательной системы определяется второй производной s = Лсоэф по времени:

Предположение о периодическом гармоническом изменении скорости и ускорения во времени наглядно подтверждается уравнениями (13.1)и(13.2)и очевидно из рис. 13.3. Фазы скорости и ускорения отличаются от фазы s = ^4cos(p соответственно на к / 2 и п. Поэтому скорость и ускорение достигают своих амплитудных значений ±А(о и ±А(о 2 соответственно в моменты времени, когда s = 0 и s = ±А. Знак ускорения всегда противоположен знаку смещения, т.е. ускорение центростремительно.

Из уравнения (13.2) очевидно равенство cP-s / dt 2 = —со 2 s, называемое дифференциальным уравнением гармонических колебаний:

Решением этого уравнения является s = ylcos(co/ + (р₀). Рассмотрим параметры гармонических колебаний.

Амплитуда Л — максимальное отклонение (смещение), м. Отклонение (смещение s = f(t)) — мгновенное вертикальное перемещение относительно положения равновесия, м.

Периодичность, т.е. повторяемость движения по истечении времени Т, называемая периодом колебания. Это минимальный промежуток времени, через который происходит повторение процесса. Итак, период Т= 1 / v, с, есть длительность полного колебания, т.е. промежуток времени, в течение которого фаза колебания получает приращение 2тс рад.

Число колебаний к моменту времени t равно п = t / Т. Количество повторений процесса п в течение времени t называют частотой, в данном случае колебательного процесса, v = п /1, с -1 . Следовательно, частота колебаний v = 1 / Т, с -1 = Гц, представляет собой число колебаний в единицу времени. В качестве единицы измерения частоты в СИ используется герц. 1 Гц соответствует одному колебанию в секунду.

Угловая, круговая или циклическая частота, называемая прежде угловой скоростью, со = Аф / At. Так как со Г = 2к, то со = 2к / Т = = 27iv, рад/с. Заметим, что Т= 2л / со. Циклическая частота равна величине изменения фазы в единицу времени, т.е. скорости изменения фазы.

Фаза ф = Ш + ф₀ = 2nt / Т + ф₀ = 2nvt + ф₀, рад, — термин греческого происхождения и в переводе на русский язык означает «проявление». В физике это следует понимать как конкретную в фиксированный момент времени стадию развития периодического процесса. Например: начало процесса, максимум развития, минимум и т.д. Однако изложенного определения фазы как физической величины недостаточно. Физический смысл фазы состоит в том, что она определяет смещение в любой момент времени и, следовательно, состояние колебательной системы. Фазам, различающимся между собой на величину, кратную 2п рад, соответствуют одинаковые смещения. Отметим еще раз, что изменение фазы на 2тс рад соответствует отрезку времени в один период Т. Кроме того, пересчет радиан в градусы осуществляется следующим образом: ф° = ф_рад • 57,3°.

Начальная фаза ф₀, рад, — значение фазы в момент начала колебаний при t = 0. При определении фазы необходимо учитывать начальную фазу ф₀ (рис. 13.4).

Время t отсчитывается от момента начала колебаний.

Большинство реальных колебательных процессов не являются строго периодическими. И в связи с этим изменение амплитуды позволяет выделить незатухающие, затухающие, нарастающие и ампли- тудно-модулированные колебания (рис. 13.5). Последний тип колебательного движения, в котором амплитуда периодически изменяется, называется биениями.

Видео:Прямолинейные колебания материальной точкиСкачать

Колебания материальной точки в теоретической механике

Содержание:

Колебания материальной точки:

К исследованию колебаний одной материальной точки могут быть сведены многие технические задачи

В качестве примера интегрирования дифференциальных уравнений движения рассмотрим колебания материальной точки. Еще совсем недавно изучение колебаний не входило в программу курсов теоретической механики высших учебных заведений. Но необходимость создания новых методов расчета всевозможных машин и различных сооружений, обладающих большой прочностью при небольшом весе, а также необходимость увеличения скоростей и производигельности машин стимулировали быстрое развитие раздела динамики, называемого теорией колебаний. Раздел, посвященный колебаниям, включен теперь во все программы по теоретической механике.

C основами явлений колебаний удобно ознакомиться сперва на примере, колебания одной материальной точки. Изучение вибраций одной материальной точки интересно также и потому, что к вибрации точки могут быть непосредственно приведены многие практически важные задачи.

Пусть точка M массы m притягивается к точке О силой F, пропорциональной (рис. 162) расстоянию ОМ, а начальная скорость точки M направлена по прямой OM или равна нулю. В таком случае точка M будет двигаться по прямолинейной траектории, вдоль которой мы направим ось х. Начало координат возьмем в точке О (в равновесном положении). Сила F как бы стремится вернуть точку M в равновесное положение О, за что ее называют восстанавливающей силой. Примером такой силы могут служить сила упругости стержня, совершающего малые колебания, или равнодействующая сил веса G и натяжения T нити при малых колебаниях маятника и т. и. Чем больше координата х, тем больше величина этой силы. Вместе с тем сила (точнее говоря, ее проекция на ось Ох) по знаку всегда противоположна знаку координаты х. В самом деле, если точка M находится справа от x начала координат О, то координата х положительна, а сила направлена в отрицательную сторону, и наоборот, если координата х отрицательна, то восстанавливающая сила направлена в положительную сторону. Обозначив коэффициент пропорциональности между силой и расстоянием через с (причем с > 0), выразим восстанавливающую силу формулой

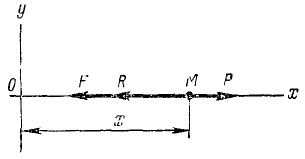
Рис. 162

Пусть на точку M во время ее движения действует сила сопротивления R, пропорциональная скорости точки и направленная против скорости. Таким образом, если точка M движется вправо (х > 0), то сила сопротивления направлена влево (R 0. Обозначив коэффициент пропорциональности через а (причем а > 0), мы определим силу сопротивления (выражаясь точнее, ее проекцию на ось Ох) формулой

Кроме того, пусть на точку M действует возмущающая сила Р, т. е. некоторая дополнительная сила, вызывающая изменение движения, обусловленного основной силой F. Возмущающая сила направлена по прямолинейной траектории точки M и, периодически изменяя свою величину и знак, раскачивает точку M то в ту, то в другую сторону. Мы ограничимся рассмотрением простейшего случая и предположим, что сила P изменяется с течением времени по закону синуса:

P = H sin pt. (133)

Очевидно, что сила P изменяется в пределах от +Н до —Н. Пример такой силы приведен в задаче № 110.

Напишем дифференциальное уравнение движения точки M:

Разделив обе части уравнения на т, введем обозначения

(134)

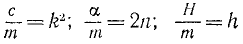
и перенесем члены, содержащие х или его производные, влево:

х + 2nx + k 2 x =h sin pt. (135)

Мы имеем неоднородное линейное дифференциальное уравнение с постоянными коэффициентами. Общее решение такого уравнения складывается из: 1) общего решения соответствующего однородного уравнения, т. е. уравнения (135) без правой части, и какого-либо частного решения неоднородного уравнения (135).

Для интегрирования уравнения

х + 2nx + k 2 x = 0

составим характеристическое уравнение

z 2 + 2nz + k 2 = 0.

Если n 2 sin (pt— δ)

и подставим в (135) написанное выражение х и его производных:

— Bp 2 sin (pt — δ) + 2nBp cos (pt — δ) + k 2 B sin (pt — δ) = h sin pt.

Преобразуем правую часть этого равенства:

h sin pt = h sin (pt — δ +δ) = h sin (pt — δ) cos ∂ + h cos (pt — δ) sin δ.

Перенеся все члены влево и собирая члены, содержащие sin(pt— δ) и cos (pt — δ), получим

[В (k 2 —p 2 )-h cos δ] sin (pt — δ) + (2Bnp-hsin δ) cos (pt — δ) = O.

Это равенство обращается в тождество, если

В (k 2 — р 2 ) = h cos δ; 2Bnp = h sin δ,

(137)

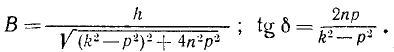
Складывая общее решение (136) однородного уравнения с найденным частным решением неоднородного уравнения, получим общее решение неоднородного уравнения (135) в таком виде:

(138)

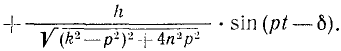
Прежде чем исследовать сложное колебательное движение точки под действием сил F, R и P, выражаемое уравнением (138), рассмотрим более простые движения, которые точка совершала’ бы под действием одной силы F или же под действием силы F и какой-либо- одной из двух остальных R или Р.

Точка, движущаяся по прямой, совершает под действием восстанавливающей силы гармоническое колебание

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Свободные колебания без сопротивления

Предположим, что на материальную точку M (см. рис. 162 на стр. 274) действует только восстанавливающая сила (131), сила же сопротивления (132) и возмущающая сила (133) равны нулю. Пусть начальная скорость точки M направлена по прямой MO или равна нулю. В таком случае точка M будет двигаться по прямой OM (по оси Ох), дифференциальное и кинематическое уравнения ее движения мы получим, положив в (135) и в (138) n и h равными нулю. В самом деле, если сила сопротивления R=O, то, следовательно, α = 0, потому что R=— ах и х переменная величина. Если же a = 0, то равно нулю и n, которое согласно (134) равно 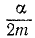. Аналогично, равенство нулю возмущающей силы означает, что равны нулю H и h.

В таком случае уравнение (135) принимает вид

Этому уравнению придадим более удобный вид, для чего выразим, постоянные интегрирования C₁ и C₂ через две другие постоянные величины А и β, однозначно связанные с C₁ и C₂ соотношениями

x = A sin (kt+ β). (140)

Это уравнение является одним из важнейших уравнений в теории колебаний и описывает наиболее простое колебательное движение, называемое гармоническим. Еще в древности было известно, что если некоторая точка M’ (рис. 163) равномерно движется по окружности радиуса О’М’ — А со скоростью kA, то проекция M этой точки на какую-либо ось Ох, лежащую в плоскости окружности, совершает гармонические колебания. Мы воспользуемся рис. 163, чтобы нагляднее ознакомить читателя с параметрами гармонического колебания.

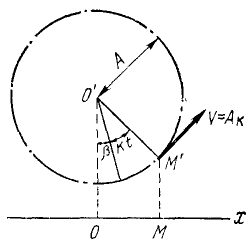
Рис. 163

Если точка M’ опишет полную окружность, то точка M’ совершит одно полное колебание.

Время одного полного колебания точки M (или, что то же, время,в течение которого точка M’ описывает одну полную окружность) называют периодом -τ₀ колебаний.

Угловая скорость k, с которой поворачивается радиус-вектор 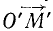при равномерном движении точки M’, равна циклической, круговой или угловой частоте колебаний точки М. Эту величину обычно коротко называют частотой, хотя, как будет видно из дальнейшего, оба понятия не вполне идентичны.

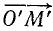
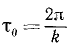
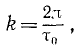
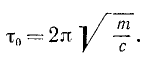
Период и угловая частота связаны простым соотношением, которое становится очевидным, если учесть, что τ₀—это время, в течение которого , вращаясь с угловой скоростью k, поворачивается на 2π:

и (141)

(142)

Период имеет размерность времени

Частота имеет размерность угловой скорости

Из (141) видно, что круговая частота k равна числу полных колебаний, совершаемых в 2π сек. Частота ν колебаний пропорциональна круговой (циклической, угловой) частоте k и равна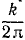. В технике и в физике частоту обычно измеряют в герцах (гц). 1 гц — частота, равная одному полному колебанию (циклу) в секунду. Иначе говоря, герц есть частота такого периодического процесса, который повторяется каждую секунду. Обратите внимание на то, что частота и период гармонических колебаний зависят от массы точки и коэффициента с восстанавливающей силы и не зависят от начальных данных.

Максимальное отклонение А точки M от среднего (равновесного) положения О в ту или в другую сторону (или, что то же, радиус круговой траектории точки М’) называют амплитудой. Амплитуду измеряют в единицах длины:

Аргумент синуса (kt + β) называют фазой колебания, a β—начальной фазой. Физический смысл фазы колебания выявляется при сравнении двух колебаний с одинаковыми частотами, но с разными начальными фазами. Колебание с фазой (kt+ β) опережает колебание с фазой kt, а колебание с фазой (kt — β) отстает от него (разумеется, при положительном β).

Напомним, что А и β являются постоянными интеграции, а следовательно, их определяют по начальным данным. Пусть в начальное мгновение t = 0, x=x₀ и x=x₀. Продифференцировав (140) по времени, получим х = Ak cos (kt + β), и подставляя начальные значения:

(143)

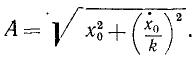
Из тех же равенств можно определить и начальную фазу 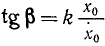. Амплитуда и начальная фаза зависят от частоты и от начальных данных.

Задача №1

Груз весом 2 T подвешен на тросе (рис. 164). При равномерном спуске груза со скоростью υ = 5м/сек произошла неожиданная задержка верхнего конца троса вследствие защемления троса в обойме блока. Пренебрегая весом троса, определить его наибольшее натяжение при последующих колебаниях груза, если коэффициент жесткости троса с = 4 T/см.

Решение. Примем следующие единицы измерений: длина—в см, время — в сек, сила—в Т. Рассмотрим движение груза. На груз действуют две силы: вертикально вниз вес груза 2T, вертикально вверх — натяжение троса. Груз спускался равномерно, следовательно, до защемления натяжение троса равнялось весу груза. В этом равновесном положении его застала авария. После защемления троса груз не остановился мгновенно. В это мгновение он имел скорость 5 м/сек и продолжал опускаться. Но по мере опускания груза сила натяжения троса возрастала от своего начального значения 2T. Ускорение груза направлено по силе и пропорционально ей. Поэтому опускание груза было замедленным и в некоторое мгновение скорость груза, перейдя через нуль, стала направленной вверх, в направлении силы и ускорения. Движение вверх было ускоренным, но по мере того как груз поднимался, растяжение троса, а следовательно, и его натяжение уменьшались, а потому уменьшалось ускорение груза, скорость же продолжала увеличиваться до момента прохождения через равновесное положение. После этого груз, набрав скорость, продолжал подниматься, ио замедленно, так как натяжение троса стало меньше силы веса и равнодействующая приложенных к грузу сил была направлена вниз. Затем скорость стала равной нулю, груз начал падать вниз, натяжение троса возрастало и движение повторялось снова неопределенное количество раз.

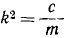
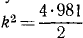
Начало О системы отсчета выберем обязательно в равновесном положении груза, относительно которого происходят колебания, направив ось Ox вертикально вниз (рис. 164). В начальное мгновение (в момент защемления троса) было: x₀= 0; x₀= 500 см/сек. Квадрат круговой частоты определим по (134). После подстановки в формулу имеем . Определим амплитуду по формуле (143):

Таким образом, при равновесном положении груза натяжение троса равно 2T; когда же груз опустился на одну амплитуду, то трос растянулся еще на 11,28 см, а при жесткости троса в 4 T/см натяжение его увеличилось еще на 45,12 Т.

Натуральный логарифм отношения двух последующих амплитуд затухающих колебаний называют логарифмическим декрементом

Видео:Свободные колебания материальной точки 1Скачать

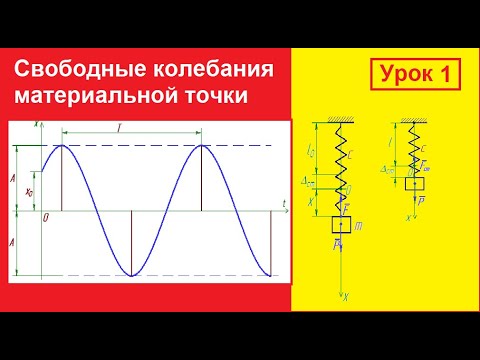
Свободные колебания с сопротивлением

Движение под действием восстанавливающей силы и силы сопротивления будем называть свободными колебаниями. Мы только что убедились, что свободные колебания без сопротивления являются гармоническими и, раз возникнув, они повторялись бы до тех пор, пока их не прекратила бы или не изменила бы какая-нибудь внешняя сила. Пусть возмущающая сила отсутствует (P = 0, H = 0, h = 0), а на точку действуют силы F=-cx и R =—ах. Дифференциальное уравнение (135) движения точки M принимает вид

х + 2nx 4- k 2 x = 0, (144)

а его интеграл получим, положив в (138) h=0:

или, если воспользуемся соотношениями (140),

(145)

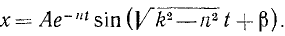
Постоянные А и β определяют по начальным данным.

Наиболее существенное отличие уравнения (145) от уравнения (140), иначе говоря, наиболее существенное изменение в свободном колебании точки М, внесенное наличием силы сопротивления, заключается в множителе e -nt , который с течением времени непрерывно уменьшается, вследствие чего амплитуда Ae -nt колебаний с сопротивлением убывает по экспоненциальному закону, асимптотически приближаясь к нулю. Такое колебание называют затухающим.

Переходя к определению периода затухающих колебаний, обратим внимание на то, что вообще периодом периодического движения называют промежуток времени между двумя последовательными прохождениями точки (или системы) через одно и то же положение водном и том же направлении. В случае затухающих колебаний только равновесное положение удовлетворяет такому определению периода, через всякое же другое положение точка M (или любая система, совершающая затухающие колебания) проходит через неравные промежутки времени (см. рис. 165). Поэтому под периодом затухающих колебаний понимают промежуток времени τ₁ между двумя последовательными прохождениями точки M (или системы) через положение равновесия в одинаковом направлении. В таком же смысле колебания, описываемые уравнением (145), могут быть названы изохронными. Период затухающих колебаний можно определить но формуле

(146)

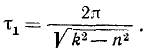
Проф. И. М. Бабаков в учебнике «Теория колебаний» рекомендует для практических расчетов более удобную формулу:

(146 / )

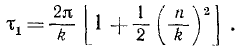
Сравнивая (141) и (146), мы видим, что сопротивление увеличивает период свободных колебаний, но незначительно.

Гораздо больше оно влияет на убывание амплитуд. Так, например, при n = 0,05 k сопротивления увеличивают период на 0,125%, а амплитуда за время одного полного колебания уменьшается более чем на 25%. На рис. 165 изображен график затухающих колебаний для случая n = 0,05 k, позаимствованный из «Лекций» проф. Е. Л. Николаи.

Отношение абсолютных значений двух последовательных амплитудных отклонений точки от равновесного положения называют коэффициентом затухания:

(147)

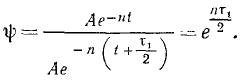
Для характеристики быстроты убывания амплитуды удобнее пользоваться натуральным логарифмом коэффициента затухания, называемым логарифмическим декрементом колебаний:

(147 / )

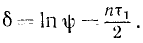
На рис. 165 пунктиром изображены кривые, уравнения которых x= Ае -n и х = —Ae -nt . График затухающих колебаний расположен между этими двумя кривыми и поочередно их касается.

Задача №2

Маятник, масса которого равна 1 кг и период качания в безвоздушной среде τ₀=l сек, заставили качаться вереде, сопротивляющейся но закону R =—2х н. Определить: 1) период затухающих колебаний маятника и 2) уменьшение амплитуды в течение трех периодов.

Решение. Определим параметры колебаний.

Круговая частота. Период τ₀=l сек= 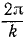, откуда k=2π = G,28.

Коэффициент α=2; m=1; 2n=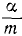, откуда n=l.

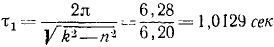
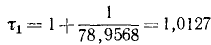
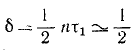
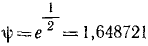
Период затухающих колебаний , или по (146′),
. Логарифмический декремент . Коэффициент затухания .

Отношение каждого максимального отклонения к последующему (через полпериода) равно коэффициенту затухания, следовательно, если амплитуду при первом размахе принять за 1, то следующие уменьшаются в отношении .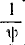

Под действием восстанавливающей и возмущающей сил точка совершает сложное колебание, являющееся результатом наложения трех гармонических колебаний: свободного, сопровождающего свободного и вынужденного

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Вынужденные колебания без сопротивления

Пусть на точку М, движущуюся по оси Ох, действуют две силы — восстанавливающая F=— CX и возмущающая P =H sin pt, направленные также по оси Ох. Величина pt может быть названа фазой силы, постоянную р назовем круговой частотой возмущающей силы, а период этих изменений обозначим через τ. Действие сопротивления мы пока не учитываем, поэтому, положив в уравнении (135) n = 0, получим следующее дифференциальное уравнение вынужденных колебаний без сопротивления:

x+ k 2 x = h sin pt. (148)

Чтобы найти решение этого уравнения, надо в (138) положить равным нулю не только n, но и δ, так как согласно (137) δ = 0 при n = 0. Имеем

Определим постоянные. Если в начальное мгновение х = x₀ и x = χ₀, то

(149)

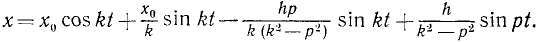
Первые два слагаемых описывают свободные колебания с частотой k. Воспользовавшись соотношениями (140″), эти два слагаемых можно представить в виде x₁ = A sin (kt + β). Если в начальное мгновение х = х= 0, то эти колебания во все время действия возмущающей силы не возникают. Третье слагаемое

— гармоническое колебание, происходящее с частотой k свободных колебаний, но с амплитудой, зависящей от возмущающей силы. Это колебание всегда, при любых начальных условиях, сопровождает вынужденные колебания и его называют свободным сопровождающим колебанием. Четвертое слагаемое

(149 / )

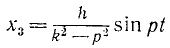
описывает вынужденные колебания. Таким образом, колебания точки являются результатом линейного наложения трех гармонических колебаний: 1) свободных, 2) сопровождающих свободных и 3) вынужденных (рис. 166):

(149 // )

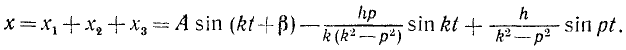
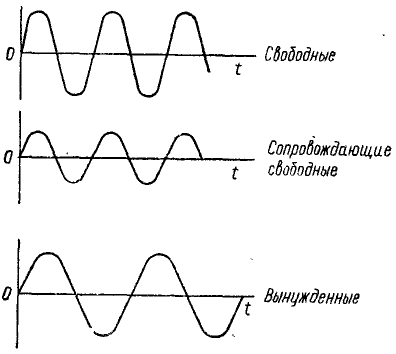
Рис. 166

На схеме (рис. 166) приведены только частоты этих колебаний, но разумеется, не изображены амплитуды и начальные фазы.

Вынужденные колебания происходят с частотой р, равной частоте возмущающей силы. Они не зависят от начальных данных.

Как видно из (143), для изменения амплитуды свободных колебаний достаточно изменить начальное отклонение или начальную скорость. Напротив, для изменения амплитуды вынужденных колебаний надо изменить возмущающую силу, что обычно бывает сопряжено с необходимостью преобразования конструкции.

Если частота р вынужденных колебаний меньше частоты k собственных (случай «малой» частоты), то амплитуда вынужденных колебаний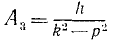, а фаза pt вынужденных колебаний совпадет
с фазой pt возмущающей силы. По если р > k (случай «большой» частоты), то выражение, написанное для А₃, становится отрицательным, однако амплитуда не может быть отрицательной. Это кажущееся несоответствие объясняется тем, что при р > k фаза вынужденных колебаний противоположна фазе возмущающей силы и уравнение вынужденных колебаний имеет вид

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Резонанс

Если частоты собственных и вынужденных колебаний близки между собой, то амплитуды получаются очень большими. Напомним, что при интегрировании уравнения (135) мы положили p≠k. Если р= k, то дифференциальное уравнение (148) имеет вид

x-k 2 x = h sin kt (148′)

Будем искать частное решение вида

Определив х =— 2Bk sin kt— Btk 2 cos kt и подставив его вместе с х в дифференциальное уравнение, получим
— 2Bk sin kt = h sin kt,

Находим общее решение дифференциального уравнения движения:

Дифференцируем по времени:

Если в начальное мгновение x=x₀ и x=x₀, то

и общее решение принимает вид

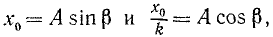
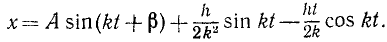
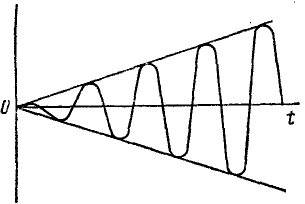
или, полагая получим

(148»’)

Следовательно, и при равенстве частот движение точки состоит из трех колебательных движений, однако вынужденные колебания представлены непериодическим членом, в коэффициент которого входит множителем время. C течением времени это третье слагаемое, называемое вековым членом, безгранично растет по абсолютной величине. Размах вынужденных колебаний непрерывно растет по линейному закону. Это явление называется резонансом. График вынужденных колебаний при резонансе представлен на рис. 167.

Задача №3

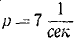
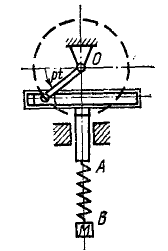
Груз M подвешен в точке В к пружине AB (рис. 168), верхний конец А которой прикреплен к поступательно движущейся кулисе. Кривошип кулисного механизма имеет длину а = 0,02 м и вращается с угловой скоростью , вследствие чего точка А совершает гармонические колебания по закону х_А =0,02 sin 7t м. Определить вынужденные колебания груза М, если его вес G = 3,6 н, а жесткость пружины с = 36 н/м.

Рис. 168

Решение. Составим дифференциальное уравнение движения груза М. Начало координат выберем в точке, с которой центр тяжести груза совладал в момент начала движения (при t = 0), когда верхний конец А пружины, совершающей гармонические колебания вместе с кулисой, занимал свое среднее положение. При сделанном нами выборе начала отсчета (в равновесном положении груза) вес G = 3,6 н уравновешивался статическим натяжением пружины с λ_cr = 36 ∙ 0,1. Наличие этих двух взаимно уравновешенных сил эквивалентно их отсутствию, а потому мы можем их отбросить и в дальнейшем рассматривать движение центра тяжести груза лишь под действием натяжения пружины, обусловленного только ее динамической деформацией, т. е. только деформацией пружины при колебании груза около равновесного положения.

При t ≠ 0 положение центра тяжести груза определяется координатой х, получающейся от суммирования двух перемещений: динамической деформации пружины и перемещения a sin pt верхнего конца А пружины. Следовательно, динамическая деформация пружины равна разности перемещений ее нижнего конца В и верхнего конца А, т. е. равна х—α sin pt . Дифференциальное уравнение движения центра груза имеет вид

mx = — с (х—a sin pt).

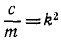
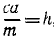
Деля обе части уравнения на m и вводя обозначения и , придадим этому уравнению знакомый нам вид (148)

x + k 2 x = h sin pt,

где

Подставляя в (149′), находим вынужденные колебания груза.
Ответ. 0,04 sin 7t.

Задача №4

Статический прогиб рессор товарного вагона равен 5 см. Определить критическую скорость вагона, при которой начнется «галопирование» вагона, если на стыках рельсов вагон испытывает толчки, вызывающие вынужденные колебания на рессорах: длина рельсов равна 12 м.

Решение. Жесткость рессор 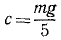, частота собственных колебаний

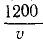
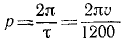
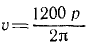
Если поезд идет со скоростью υ см/сек, то вагон получает толчки на стыках через каждые сек. Таков период τ возмущающей силы. Частота возмущающей силы , откуда . Галопирование вагона произойдет при резонансе, т. е. при равенстве частот собственных и вынужденных колебаний. Подставляя в выражение, полученное для скорости, р = k = 14, найдем

Чтобы выразить скорость в км/ч, умножим выраженную в см/ceκ скорость на 0,036.

Если к точке приложены восстанавливающая и возмущающая сила и сила сопротивления, то свободные колебания затухают и остаются только вынужденные

Видео:Колебания точкиСкачать

Влияние сопротивления на вынужденные колебания

Если на точку, кроме восстанавливающей и возмущающей сил, действует также и сила R сопротивления, то движение точки описывается дифференциальным уравнением (135) и его решением (138).

Первый член правой части (138) с возрастанием t стремится к нулю, и соответствующие ему колебания точки с течением времени затухают, поэтому ими можно пренебречь. Остаются только вынужденные колебания (рис. 169):

(150)

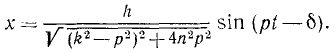
Они происходят с частотой возмущающей силы, сопротивление не влияет на период вынужденных колебаний. Амплитуда не зависит от начальных условий и времени и не изменяется с течением времени.

Предположим, что возмущающая сила сохраняет свое максимальное значение Н. При равновесии под действием такой силы и восстанавливающей силы F =— сх точка M получила бы так называемое статическое отклонение

Из этого соотношения найдем максимальное ускорение точки M под действием возмущающей силы: h=k 2 x_ст и, подставляя это значение h в выражение (150), выразим амплитуду вынужденных колебаний равенством

Отношение частоты вынужденных колебаний к частоте собственных колебаний

(151)

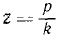
носит название коэффициента расстройки и отношение величины n, измеряемой в ceκ -1 , к частоте собственных колебаний называют безразмерным коэффициентом вязкости:

(151′)

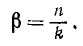
Введя эти обозначения в предыдущее равенство и разделив обе части его на x_ст, получим:

(152)

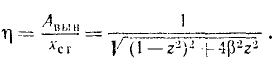
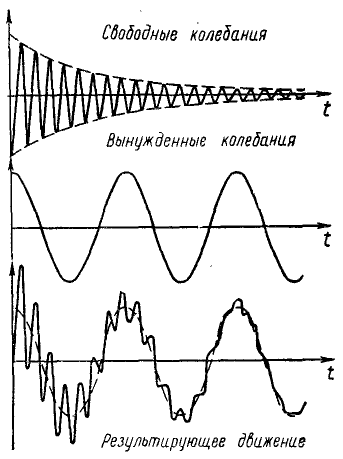
Рис. 169

Величина η—коэффициент динамичности — позволяет охарактеризовать динамический эффект, вызываемый возмущающей силой.

Коэффициент динамичности η зависит от двух величин (z и β).

Задавшись каким-либо значением β, и откладывая по оси абсцисс различные значения z, а по оси ординат—соответствующие значения коэффициента динамичности η, получим, так называемые, резонансные кривые. На рис. 170 изображены резонансные кривые для значений безразмерного коэффициента вязкости: 0,25, 0,15. и 0,10. Пунктиром нанесена уходящая в бесконечность при 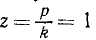резонансная кривая, соответствующая β = 0, т. е. вынужденным колебаниям без сопротивления.

Как показывает график (рис. 170) в областях, достаточно далеких от резонанса, амплитуды вынужденных колебаний с сопротивлением почти не зависят от безразмерного коэффициента вязкости. В этих областях при вычислении амплитуд вынужденных колебаний можно не учитывать сопротивлений и пользоваться более простой формулой

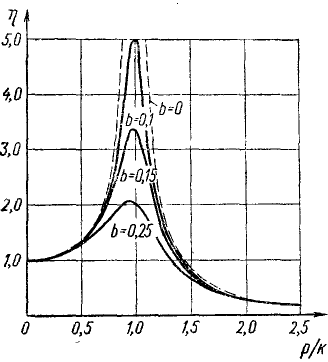
Рис. 170

При резонансе (р = k) амплитуда вынужденных колебаний при наличии сопротивлений остается конечной, но наибольшее значение амплитуда имеет, если 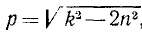, в чем легко убедиться, определив максимум амплитуды при различных р, считая h, k и п данными.

В вынужденных колебаниях с сопротивлением всегда бывает сдвиг фазы колебания по отношению к фазе .возмущающей силы. Величина этого сдвига определяется формулой (137).

Заметим, что все сказанное здесь относительно малых колебаний материальной точки полностью соответствует малым колебаниям материальной системы с одной степенью свободы.

• Количество движения
• Момент количества движения
• Мощность и работа силы
• Потенциальная энергия
• Естественный и векторный способы определения движения точки
• Координатный способ определения движения точки
• Касательное и нормальное ускорения точки
• Основные законы динамики

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

📸 Видео

Дифференциальные уравнения движения материальной точкиСкачать

Колебательное движение. Практическая часть - решение задачи. 9 класс.Скачать

Собственные частоты колебаний точкиСкачать

Свободные и вынужденные колебанияСкачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Урок 343. Затухающие колебания (часть 1)Скачать

Урок 327. Гармонические колебанияСкачать

Свободные колебания материальной точки 3Скачать

Дифференциальные уравнения движения точкиСкачать