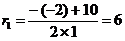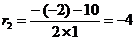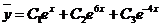Решение дифференциального уравнения с exp

Пример 1. y»’ — 2y» — 24y’ = (x+5)e 6x
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx через онлайн сервис. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 3 -2r 2 -24r = 0
Вынесем r за скобку. Получим:
r(r 2 -2r-24) = 0
Здесь r₁ = 0. Найдем остальные корни.
r 2 -2 r — 24 = 0
D = (-2) 2 — 4 • 1 • (-24) = 100


Корни характеристического уравнения:
r₁ = 0
r₂ = 6
r₃ = -4
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e 0x
y₂ = e 6x
y₃ = e -4x
Общее решение однородного уравнения имеет вид:

Рассмотрим правую часть:
f(x) = (x+5)e 6x
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = x+5, Q(x) = 0, α = 6, β = 0.
Следовательно, число α + βi = 6 + 0i является корнем характеристического уравнения кратности k = 1(r₂).
Уравнение имеет частное решение вида:

Вычисляем производные:
y’ = e 6x (2•A•x(3•x+1)+6•B•x+B)
y» = 2•e 6x (18•A•x 2 +12•A•x+A+18•B•x+6•B)
y»’ = 36•e 6x (6•A•x 2 +6•A•x+A+6•B•x+3•B)
которые подставляем в исходное дифференциальное уравнение:
y»’ -2y» -24y’ = (36•e 6x (6•A•x 2 +6•A•x+A+6•B•x+3•B)) -2(2•e 6x (18•A•x 2 +12•A•x+A+18•B•x+6•B)) -24(e 6x (2•A•x(3•x+1)+6•B•x+B)) = (x+5)•e 6•x
или
120Ax e 6•x +32A e 6•x + 60B e 6•x = (x+5)•e 6•x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
120A = 1
32A + 60B = 5
Решая ее, находим:
A = 1 /₁₂₀; B = 71 /₉₀₀

Частное решение имеет вид:
y * = x (( 1 /₁₂₀x+ 71 /₉₀₀)e 6x )
Таким образом, общее решение дифференциального уравнения имеет вид:
y = C₁ + C₂e 6 x + C₃e -4 x + x (( 1 /₁₂₀x+ 71 /₉₀₀)e 6x )

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Решение дифференциального уравнения с exp

Общее решение дифференциальных уравнений.

Для нахождения аналитических решений дифференциальных уравнений в Maple применяется команда dsolve(eq,var,options), где eq – дифференциальное уравнение, var – неизвестные функции, options – параметры. Параметры могут указывать метод решения задачи, например, по умолчанию ищется аналитическое решение: type=exact . При составлении дифференциальных уравнений для обозначения производной применяется команда diff , например, дифференциальное уравнение y» + y = x записывается в виде: diff(y(x),x$2)+y(x)=x.

Общее решение дифференциального уравнения зависит от произвольных постоянных, число которых равно порядку дифференциального уравнения. В Maple такие постоянные, как правило, обозначаются как _ С1 , _ С2 , и т.д.

Общее решение неоднородного линейного дифференциального уравнения всегда выводится так, чтобы была четко видна, структура этого решения. Как известно, общее решение неоднородного линейного дифференциального уравнения равно сумме общего решения соответствующего однородного дифференциального уравнения и частного решения этого же неоднородного дифференциального уравнения. Поэтому в строке вывода решение неоднородного линейного дифференциального уравнения всегда состоит из слагаемых, которые содержат произвольные постоянные (это общее решения соответствующего однородного дифференциального уравнения), и слагаемых без произвольных постоянных (это частное решения этого же неоднородного дифференциального уравнения).

Команда dsolve выдает решение дифференциального уравнения в невычисляемом формате. Для того, чтобы с решением можно было бы работать далее (например, построить график решения) следует отделить правую часть полученного решения командой rhs(%) .

Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Задание 1.1.

1. Найти общее решение дифференциального уравнения y ‘+ y cos x =sin x cos x .

de : =

1

Итак, решение искомого уравнения есть функция 1 .

Замечание : при записи решения диффреренциального уравнения в Maple в строке вывода произвольная постоянная обозначена как _ С1 .

2. Найти общее решение дифференциального уравнения второго порядка y » — 2 y ‘+ y =sin x + e — x .

deq :=

Замечание : так как исходное уравнение было второго порядка, то полученное решение содержит две произвольные константы, которые в Maple обычно обознаются как _ С1 и _ С2 . Первые два слагаемых представляют собой общее решение соответствующего однородного дифференциального уравнения, а вторые два – частное решение неоднородного дифференциального уравнения.

3. Найти общее решение дифференциального уравнения порядка y »+ k 2 y =sin( qx ) в двух случаях: q ¹ k и q = k (резонанс).

de :=

Теперь найдем решение в случае резонанса. Для этого перед вызовом команды dsolve следует приравнять q = k .

Замечание : в обоих случаях частное решение неоднородного уравнения и общее решение, содержащее произвольные постоянные, выводятся отдельными слагаемыми.

Фундаментальная (базисная) система решений.

Команда dsolve представляет возможность найти фундаментальную систему решений (базисные функции) дифференциального уравнения. Для этого в параметрах команды dsolve следует указать output=basis .

Видео:Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

Задание 1.2.

Найти фундаментальную систему решений дифференциального уравнения: y (4) +2 y »+ y =0.

de : =

> dsolve(de, y(x), output=basis);

Решение задачи Коши или краевой задачи.

Команда dsolve может найти решение задачи Коши или краевой задачи, если помимо дифференциального уравнения задать начальные или краевые условия для неизвестной функции. Для обозначения производных в начальных или краевых условиях используется дифференциальный оператор , например, условие y»(0)=2 следует записать в виде , или условие y ‘(1)=0: . Напомним, что производная n -го порядка записывается в виде .

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Задание 1.3.

1. Найти решение задачи Коши: y (4) + y »=2cos x , y (0)= — 2, y ‘(0)=1, y »(0)=0, y »'(0)=0.

cond:= y(0)= — 2, D(y)(0)=1, (D (2) )(y)(0)=0, (D (3) )(y)(0)=0

y( x )= — 2cos( x ) — x sin( x )+ х

2. Найти решение краевой задачи: , , . Построить график решения.

de : =

y( x )=2 x — p + p cos( x )

Замечание : для построения графика решения предварительно следует отделить правую часть полученного выражения.

Системы дифференциальных уравнений.

Команда dsolve может найти решение системы дифференциальных уравнений (или задачи Коши), если в ней указать: dsolve(,), где sys — система дифференциальных уравнений, x(t),y(t),… — набор неизвестных функций.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Задание 1.4.

Найти решение системы дифференциальных уравнений:

Найдены две функции x ( t ) и y ( t ), которые зависят от двух произвольных постоянных _ С1 и _ С2 .

Приближенное решение дифференциальных уравнений с помощью степенных рядов.

Для многих типов дифференциальных уравнений не может быть найдено точное аналитическое решение. В этом случае дифференциальное уравнение можно решить с помощью приближенных методов, и, в частности, с помощью разложения в степенной ряд неизвестной функции.

Чтобы найти приближенное решение дифференциального уравнения в виде степенного ряда, в команде dsolve следует после переменных указать параметр type=series (или просто series ). Для того, чтобы указать порядок разложения n , т.е. порядок степени, до которой производить разложение, следует перед командой dsolve вставить определение порядка с помощью команды Order:=n .

Если ищется общее решение дифференциального уравнения в виде разложения в степенной ряд, то коэффициенты при степенях х найденного разложения будут содержать неизвестные значения функции в нуле y(0) и ее производных D(y)(0), (D@@2)(y)(0) и т.д. Полученное в строке вывода выражение будет иметь вид, похожий на разложение искомого решения в ряд Маклорена, но с другими коэффициентами при степенях х . Для выделения частного решения следует задать начальные условия y(0)=у1, D(y)(0)=у2, (D@@2)(y)(0)=у3 и т.д., причем количество этих начальных условий должно совпадать с порядком соответствующего дифференциального уравнения.

Разложение в степенной ряд имеет тип series , поэтому для дальнейшей работы с этим рядом его следует преобразовать в полином с помощью команды convert(%,polynom) , а затем выделить правую часть полученного выражения командой rhs(%) .

Видео:Дифференциальные уравнения. 11 класс.Скачать

Задание 1.5.

1. Найти решение задачи Коши: , в виде степенного ряда с точностью до 5-го порядка.

y(0)=0>, y(x), type=series);

В полученном решении слагаемое означает, что точность разложения была до 5-го порядка.

2. Найти общее решение дифференциального уравнения y »( х ) — y 3 ( х )= е — х cos x , в виде разложения в степенной ряд до 4-го порядка. Найти разложение при начальных условиях: y (0)=1, y ‘(0)=0.

> restart; Order:=4: de:=diff(y(x),x$2)-

Замечание : в полученном разложении запись D(y)(0) обозначает производную в нуле: y ‘(0). Для нахождения частого решения осталось задать начальные условия:

3. Найти приближенное решение в виде степенного ряда до 6-го порядка и точное решение задачи Коши: , , , . Построить на одном рисунке графики точного и приближенного решений.

de : =

cond :=y(0)=1, D(y)(0)=1, D (2) (y)(0)=1

y( x )=

y( x )=

Замечание : тип решения дифференциального уравнения в виде ряда есть series , поэтому для дальнейшего использования такого решения (вычислений или построения графика) его обязательно следует конвертировать в полином с помощью команды convert

На этом рисунке видно, что наилучшее приближение точного решения степенным рядом достигается примерно на интервале — 1 x

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

🎥 Видео

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Задача Коши для ЛНДУ II п. (e^x)Скачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Общее и частное решение дифференциального уравненияСкачать