Пример №1 . Решить задачу методом динамического программирования в прямом и обратном времени для целевой функции, заданной таблично.
F(x1,x2,x3) = f1(x1) + f2(x2) + f3(x3) → max
x1 + 2x2 + 2x3 ≤ 5
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| f1(x1) | 6 | 7 | 11 | 12 | 15 | 16 |
| f2(x2) | 9 | 11 | 13 | 15 | ||
| f3(x3) | 8 | 12 | 14 | 16 |
Решение.
I этап. Условная оптимизация. f1(L) = max(f1); 0 ≤ x1 ≤ 5; x1 = 0,1,2,3,4,5.
f1(0) = max[6] = 6
f1(1) = max[6, 7] = 7
f1(2) = max[6, 7, 11] = 11
f1(3) = max[6, 7, 11, 12] = 12
f1(4) = max[6, 7, 11, 12, 15] = 15
f1(5) = max[6, 7, 11, 12, 15, 16] = 16
Таблица 1 – Расчет значения функции f1(L)
| L | 0 | 1 | 2 | 3 | 4 | 5 |
| f1(L) | 6 | 7 | 11 | 12 | 15 | 16 |
| x1 | 0 | 1 | 2 | 3 | 4 | 5 |
f2(L) = max[f2 + f1(L — 2x2)]; 0 ≤ x2 ≤ 5; x2 = 0,1,2,3,4,5.
f2(0) = max[9+6] = 15
f2(1) = max[9+7] = 16
f2(2) = max[9+11, 11+6] = 20
f2(3) = max[9+12, 11+7] = 21
f2(4) = max[9+15, 11+11, 13+6] = 24
f2(5) = max[9+16, 11+12, 13+7] = 25
Таблица 2 – Расчет значения функции f2(L)
| L | 0 | 1 | 2 | 3 | 4 | 5 |
| f2(L) | 15 | 16 | 20 | 21 | 24 | 25 |
| x2 | 0 | 0 | 0 | 0 | 0 | 0 |
f3(L) = max[f3 + f2(L — 2x3)]; 0 ≤ x3 ≤ 5; x3 = 0,1,2,3,4,5.
f3(0) = max[8+15] = 23
f3(1) = max[8+16] = 24
f3(2) = max[8+20, 12+15] = 28
f3(3) = max[8+21, 12+16] = 29
f3(4) = max[8+24, 12+20, 14+15] = 32
f3(5) = max[8+25, 12+21, 14+16] = 33
Таблица 3 – Расчет значения функции f3(L)
| L | 0 | 1 | 2 | 3 | 4 | 5 |
| f3(L) | 23 | 24 | 28 | 29 | 32 | 33 |
| x3 | 0 | 0 | 0 | 0 | 0 | 0 |
II этап. Безусловная оптимизация.
Таким образом, максимум f3(5) = 33
При этом x3 = 0, так как f3(5) = 33 достигается при х3=0 (см. таблицу 3).
Остальные x распределяются следующим образом:
L = 5 — 2 * 0 = 5
f2(5) = 25 достигается при х2 = 0 (см. таблицу 2).
L = 5 — 2 * 0 = 5
f1(5) = 16 достигается при х1 = 5 (см. таблицу 1).
L = 5 — 1 * 5 = 0
В итоге наилучший вариант достигается при значениях: x1 = 5, x2 = 0, x3 = 0
Пример №2 . Рассмотрим задачу об оптимальном размещении капитала K = nh в m различных независимых фондах (банки, организации, фирма и т.д.), для которых известна ожидаемая прибыль fi при капиталовложениях xi = ih, i = 1..n. Здесь n – количество дискретных приращений h (дискрет), на которые разбит капитал К.
Пусть такие данные имеются по четырем (m=4) фондам для h = 1 млн. руб., n = 6
Решение.
I этап. Условная оптимизация.
1-й шаг: k = 4.
Предположим, что все средства в количестве x4 = 6 отданы 4-у предприятию. В этом случае максимальный доход, как это видно из таблицы 1*, составит 0.56, следовательно:
F4(c4) = g4(x4)
Таблица 1.
| 0 | x1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| x4 | f0(x0) / F4(x4) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0 |
| 2 | 0.33 | 0 | 0 | 0 | 0 | 0.33 | 0 | 0 |
| 3 | 0.42 | 0 | 0 | 0 | 0.42 | 0 | 0 | 0 |
| 4 | 0.48 | 0 | 0 | 0.48 | 0 | 0 | 0 | 0 |
| 5 | 0.53 | 0 | 0.53 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0.56 | 0.56* | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 1*.
| c1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| F0(c1) | 0 | 0.2 | 0.33 | 0.42 | 0.48 | 0.53 | 0.56 |
| x1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
2-й шаг: k = 3.
Определяем оптимальную стратегию при распределении средств между остальными предприятиями. При этом рекуррентное соотношение Беллмана имеет вид:
F3(c3) = max [ g3(x3) + F4(c3 — x3)]
Таблица 2.
| 0 | x2 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| x3 | f3(x3) / F3(x3) | 0 | 0.2 | 0.33 | 0.42 | 0.48 | 0.53 | 0.56 |
| 0 | 0 | 0 | 0.2* | 0.33 | 0.42 | 0.48 | 0.53 | 0.56 |
| 1 | 0.15 | 0.15 | 0.35* | 0.48* | 0.57 | 0.63 | 0.68 | 0 |
| 2 | 0.25 | 0.25 | 0.45 | 0.58 | 0.67 | 0.73 | 0 | 0 |
| 3 | 0.4 | 0.4 | 0.6* | 0.73* | 0.82 | 0 | 0 | 0 |
| 4 | 0.5 | 0.5 | 0.7 | 0.83* | 0 | 0 | 0 | 0 |
| 5 | 0.62 | 0.62 | 0.82 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0.73 | 0.73 | 0 | 0 | 0 | 0 | 0 | 0 |
Заполняем таблицу 2*. Для этого на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение x2.
Таблица 2*.
| c2 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| F3(c2) | 0 | 0.2 | 0.35 | 0.48 | 0.6 | 0.73 | 0.83 |
| x2 | 0 | 0 | 1 | 1 | 3 | 3 | 4 |
3-й шаг: k = 2.
Определяем оптимальную стратегию при распределении средств между остальными предприятиями. При этом рекуррентное соотношение Беллмана имеет вид:
F2(c2) = max [ g2(x2) + F3(c2 — x2)]
Таблица 3.
| 0 | x3 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| x2 | f4(x4) / F2(x2) | 0 | 0.2 | 0.35 | 0.48 | 0.6 | 0.73 | 0.83 |
| 0 | 0 | 0 | 0.2 | 0.35 | 0.48 | 0.6 | 0.73 | 0.83 |
| 1 | 0.25 | 0.25* | 0.45* | 0.6 | 0.73 | 0.85 | 0.98 | 0 |
| 2 | 0.41 | 0.41 | 0.61* | 0.76* | 0.89 | 1.01 | 0 | 0 |
| 3 | 0.55 | 0.55 | 0.75 | 0.9* | 1.03* | 0 | 0 | 0 |
| 4 | 0.65 | 0.65 | 0.85 | 1 | 0 | 0 | 0 | 0 |
| 5 | 0.75 | 0.75 | 0.95 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0.8 | 0.8 | 0 | 0 | 0 | 0 | 0 | 0 |
Заполняем таблицу 3*. Для этого на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение x3.
Таблица 3*.
| c3 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| F4(c3) | 0 | 0.25 | 0.45 | 0.61 | 0.76 | 0.9 | 1.03 |
| x3 | 0 | 1 | 1 | 2 | 2 | 3 | 3 |
4-й шаг: k = 1.
Определяем оптимальную стратегию при распределении средств между остальными предприятиями. При этом рекуррентное соотношение Беллмана имеет вид:
F1(c1) = max [ g1(x1) + F2(c1 — x1)]
Таблица 4.
| 0 | x4 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| x1 | f5(x5) / F1(x1) | 0 | 0.25 | 0.45 | 0.61 | 0.76 | 0.9 | 1.03 |
| 0 | 0 | 0 | 0.25 | 0.45 | 0.61 | 0.76 | 0.9 | 1.03 |
| 1 | 0.28 | 0.28* | 0.53* | 0.73* | 0.89 | 1.04 | 1.18 | 0 |
| 2 | 0.45 | 0.45 | 0.7 | 0.9 | 1.06 | 1.21 | 0 | 0 |
| 3 | 0.65 | 0.65 | 0.9* | 1.1* | 1.26* | 0 | 0 | 0 |
| 4 | 0.78 | 0.78 | 1.03 | 1.23 | 0 | 0 | 0 | 0 |
| 5 | 0.9 | 0.9 | 1.15 | 0 | 0 | 0 | 0 | 0 |
| 6 | 1.02 | 1.02 | 0 | 0 | 0 | 0 | 0 | 0 |
Заполняем таблицу 4*. Для этого на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение x4.
Таблица 4*.
| c4 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| F5(c4) | 0 | 0.28 | 0.53 | 0.73 | 0.9 | 1.1 | 1.26 |
| x4 | 0 | 1 | 1 | 1 | 3 | 3 | 3 |
II этап. Безусловная оптимизация.
1-й шаг: k = 1.
По данным таблицы 4* максимальный доход при распределении 6 между предприятиями составляет c1 = 6, F1(6) = 1.26. При этом 1-му предприятию нужно выделить x1 = 3.
2-й шаг: k = 2.
Определим величину оставшихся денежных средств, приходящихся на долю остальных предприятий.
c2 = c1 — x1 = 6 — 3 = 3.
По данным таблицы 3* максимальный доход при распределении 3 между предприятиями составляет c2 = 3, F2(3) = 0.61. При этом 2-му предприятию нужно выделить x2 = 2.
3-й шаг: k = 3.
Определим величину оставшихся денежных средств, приходящихся на долю остальных предприятий.
c3 = c2 — x2 = 3 — 2 = 1.
По данным таблицы 2* максимальный доход при распределении 1 между предприятиями составляет c3 = 1, F3(1) = 0.2. При этом 3-му предприятию нужно выделить x3 = 0.
4-й шаг: k = 4.
Определим величину оставшихся денежных средств, приходящихся на долю остальных предприятий.
c4 = c3 — x3 = 1 — 0 = 1.
По данным таблицы 1* максимальный доход при распределении 1 между предприятиями составляет c4 = 1, F4(1) = 0.20. При этом 4-му предприятию нужно выделить x4 = 1.
Таким образом, оптимальный план инвестирования предприятия: x1 = 3, x2 = 2, x3 = 0, x4 = 1, который обеспечит максимальный доход, равный: F(6) = g1(3) + g2(2) + g3(0) + g4(1) = 0.65 + 0.41 + 0 + 0.20 = 1.26.
Пример №3 . Распределите c=200 млн ден. ед. инвестиций между четырьмя министерствами республики ( n=4 ) на реконструкцию и модернизацию производственных мощностей таким образом, чтобы суммарный прирост производства продукции всех министерств f4(с) был максимальным. Прирост выпуска продукции в каждом из министерств gi(x) в зависимости от объема выделенных средств x (0 c=200 млн ден. ед. между первыми тремя министерствами, максимизирующее их суммарный прирост производства продукции f3(с).
Примечание. Основная задача решается с помощью процедуры прямой прогонки. Ответ на подзадачу можно получить из таблицы n-1 исходного решения.
Видео:Частное решение дифференциального уравнения. 11 класс.Скачать
Дифференциальные уравнения по-шагам
Видео:6-5. Алгоритм прогонкиСкачать
Результат
Примеры дифференциальных уравнений
- Простейшие дифференциальные ур-ния 1-порядка
- Дифференциальные ур-ния с разделяющимися переменными
- Линейные неоднородные дифференциальные ур-ния 1-го порядка
- Линейные однородные дифференциальные ур-ния 2-го порядка
- Уравнения в полных дифференциалах
- Решение дифференциального уравнения заменой
- Смена y(x) на x в уравнении
- Другие
Указанные выше примеры содержат также:
- квадратные корни sqrt(x),
кубические корни cbrt(x) - тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x) - натуральные логарифмы ln(x),
десятичные логарифмы log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
asinh(x), acosh(x), atanh(x), actanh(x) - число Пи pi
- комплексное число i
Правила ввода
Можно делать следующие операции
2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5
Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
💥 Видео
Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать
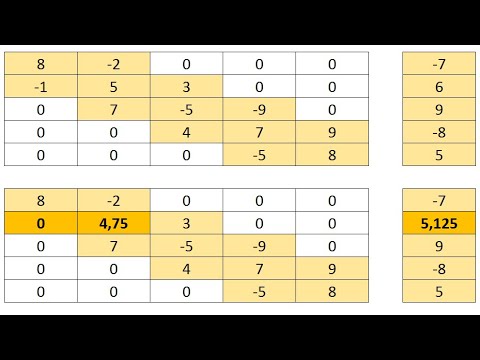
2.1 Точные методы решения СЛАУ (Крамера, Гаусса, Жордана, прогонки)Скачать
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
Решение системы дифференциальных уравнений методом ЭйлераСкачать
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать
Решение системы уравнений методом ГауссаСкачать
Методы решения нелинейных краевых задач для ОДУСкачать
Сеточные методы решения дифференциальных уравнений в частных производных.Скачать
13. Как решить дифференциальное уравнение первого порядка?Скачать
9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать
Пример 65. Решить задачу Коши (диффуры)Скачать
Математика без Ху!ни. Метод Гаусса.Скачать
Метод Гаусса решения СЛАУ. Метод прогонки. Итерационные методы. Численные методы. Лекция №3Скачать
Дифференциальные уравнения. 11 класс.Скачать
