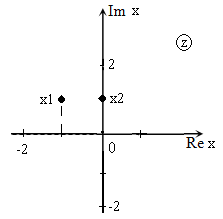Решение биквадратных уравнений в комплексных числах (5 видео)

Решение биквадратных уравнений в комплексных числах

. Вы вводите его по ссылке решение уравнений онлайн , указываете, что i — это комплексная единица (после того как ввели уравнение и нажали кнопку «решить»), нажимаете кнопку под формой «Обновить» и получаете ответ как здесь. Если в ответе присутствуют корни из комплексных чисел, то можно воспользоваться калькулятором по упрощению комлексных чисел по ссылке

Содержание

Решение уравнений четвертой степени
Решение двучленного уравнения четвертой степени
Решение возвратного уравнения четвертой степени
Решение биквадратного уравнения
Решение уравнений четвертой степени с рациональными корнями
Решение уравнений четвертой степени по методу Феррари
Решение квадратных уравнений с помощью комплексных чисел
💥 Видео

Видео:Биквадратное уравнение. Комплексные корни.Скачать

Решение уравнений четвертой степени

Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.

Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.

Видео:Комплексные числа в уравненияхСкачать

Решение двучленного уравнения четвертой степени

Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид A x 4 + B = 0 .

Для решения этого типа уравнений применяются формулы сокращенного умножения:

A x 4 + B = 0 x 4 + B A = 0 x 4 + 2 B A x 2 + B A — 2 B A x 2 = 0 x 2 + B A 2 — 2 B A x 2 = 0 x 2 — 2 B A 4 x + B A x 2 + 2 B A 4 x + B A = 0

Остается лишь найти корни квадратных трехчленов.

Решить уравнение четвертой степени 4 x 4 + 1 = 0 .

Решение

Для начала проведем разложение многочлена 4 x 4 + 1 на множители:

4 x 4 + 1 = 4 x 4 + 4 x 2 + 1 = ( 2 x 2 + 1 ) 2 — 4 x 2 = 2 x 2 — 2 x + 1 ( 2 x 2 + 2 x + 1 )

Теперь найдем корни квадратных трехчленов.

2 x 2 — 2 x + 1 = 0 D = ( — 2 ) 2 — 4 · 2 · 1 = — 4 x 1 = 2 + D 2 · 2 = 1 2 + i x 2 = 2 — D 2 · 2 = 1 2 — i

2 x 2 + 2 x + 1 = 0 D = 2 2 — 4 · 2 · 1 = — 4 x 3 = — 2 + D 2 · 2 = — 1 2 + i x 4 = — 2 — D 2 · 2 = — 1 2 — i

Мы получили четыре комплексных корня.

Ответ: x = 1 2 ± i и x = — 1 2 ± i .

Видео:Комплексные корни квадратного уравненияСкачать

Решение возвратного уравнения четвертой степени

Возвратные уравнения четвертого порядка имеют вид A x 4 + B x 3 + C x 2 + B x + A = 0

х = 0 не является корнем этого уравнения: A · 0 4 + B · 0 3 + C · 0 2 + B · 0 + A = A ≠ 0 . Поэтому на x 2 можно смело разделить обе части этого уравнения:

A x 4 + B x 3 + C x 2 + B x + A = 0 A x 2 + B x + C + B x + A x 2 = 0 A x 2 + A x 2 + B x + B x + C = 0 A x 2 + 1 x 2 + B x + 1 x + C = 0

Проведем замену переменных x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2 :

A x 2 + 1 x 2 + B x + 1 x + C = 0 A ( y 2 — 2 ) + B y + C = 0 A y 2 + B y + C — 2 A = 0

Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.

Найти все комплексные корни уравнения 2 x 4 + 2 3 + 2 x 3 + 4 + 6 x 2 + 2 3 + 2 x + 2 = 0 .

Решение

Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x 2 :

2 x 2 + 2 3 + 2 x + 4 + 6 + 2 3 + 2 x + 2 x 2 = 0

2 x 2 + 2 x 2 + 2 3 + 2 x + 2 3 + 2 x + 4 + 6 + = 0 2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0

Проведем замену переменной x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2

2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0 2 y 2 — 2 + 2 3 + 2 y + 4 + 6 = 0 2 y 2 + 2 3 + 2 y + 6 = 0

Решим полученное квадратное уравнение:

D = 2 3 + 2 2 — 4 · 2 · 6 = 12 + 4 6 + 2 — 8 6 = = 12 — 4 6 + 2 = 2 3 — 2 2 y 1 = — 2 3 — 2 + D 2 · 2 = — 2 3 — 2 + 2 3 — 2 4 = — 2 2 y 2 = — 2 3 — 2 — D 2 · 2 = — 2 3 — 2 — 2 3 + 2 4 = — 3

Вернемся к замене: x + 1 x = — 2 2 , x + 1 x = — 3 .

Решим первое уравнение:

x + 1 x = — 2 2 ⇒ 2 x 2 + 2 x + 2 = 0 D = 2 2 — 4 · 2 · 2 = — 14 x 1 = — 2 — D 2 · 2 = — 2 4 + i · 14 4 x 2 = — 2 — D 2 · 2 = — 2 4 — i · 14 4

Решим второе уравнение:

x + 1 x = — 3 ⇒ x 2 + 3 x + 1 = 0 D = 3 2 — 4 · 1 · 1 = — 1 x 3 = — 3 + D 2 = — 3 2 + i · 1 2 x 4 = — 3 — D 2 = — 3 2 — i · 1 2

Ответ: x = — 2 4 ± i · 14 4 и x = — 3 2 ± i · 1 2 .

Видео:Решение квадратных уравнений на множестве комплексных чиселСкачать

Решение биквадратного уравнения

Биквадратные уравнения четвертой степени имеют вид A x 4 + B x 2 + C = 0 . Мы можем свести такое уравнение к квадратному A y 2 + B y + C = 0 путем замены y = x 2 . Это стандартный прием.

Решить биквадратное уравнение 2 x 4 + 5 x 2 — 3 = 0 .

Решение

Выполним замену переменной y = x 2 , что позволит нам свести исходное уравнение к квадратному:

2 y 2 + 5 y — 3 = 0 D = 5 2 — 4 · 2 · ( — 3 ) = 49 y 1 = — 5 + D 2 · 2 = — 5 + 7 4 = 1 2 y 2 = — 5 — D 2 · 2 = — 5 — 7 4 = — 3

Следовательно, x 2 = 1 2 или x 2 = — 3 .

Первое равенство позволяет нам получить корень x = ± 1 2 . Второе равенство не имеет действительных корней, зато имеет комплексно сопряженных корней x = ± i · 3 .

Ответ: x = ± 1 2 и x = ± i · 3 .

Найти все комплексные корни биквадратного уравнения 16 x 4 + 145 x 2 + 9 = 0 .

Решение

Используем метод замены y = x 2 для того, чтобы свести исходное биквадратное уравнение к квадратному:

16 y 2 + 145 y + 9 = 0 D = 145 2 — 4 · 16 · 9 = 20449 y 1 = — 145 + D 2 · 16 = — 145 + 143 32 = — 1 16 y 2 = — 145 — D 2 · 16 = — 145 — 143 32 = — 9

Поэтому, в силу замены переменной, x 2 = — 1 16 или x 2 = — 9 .

Ответ: x 1 , 2 = ± 1 4 · i , x 3 , 4 = ± 3 · i .

Видео:10 класс, 35 урок, Комплексные числа и квадратные уравненияСкачать

Решение уравнений четвертой степени с рациональными корнями

Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».

Видео:Решение квадратных уравнений в поле комплексных чиселСкачать

Решение уравнений четвертой степени по методу Феррари

Уравнения четвертой степени вида x 4 + A x 3 + B x 2 + C x + D = 0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y 0 . Это любой из корней кубического уравнения y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 . После этого необходимо решить два квадратных уравнения x 2 + A 2 x + y 0 2 + A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 , у которых подкоренное выражение является полным квадратом.

Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.

Найти корни уравнения x 4 + 3 x 3 + 3 x 2 — x — 6 = 0 .

Решение

Имеем А = 3 , В = 3 , С = — 1 , D = — 6 . Применим метод Феррари для решения данного уравнения.

Составим и решим кубическое уравнение:
y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 y 3 — 3 y 2 + 21 y — 19 = 0

Одним из корней кубического уравнения будет y 0 = 1 , так как 1 3 — 3 · 1 2 + 21 · 1 — 19 = 0 .

Запишем два квадратных уравнения:
x 2 + A 2 x + y 0 2 ± A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 x 2 + 3 2 x + 1 2 ± 1 4 x 2 + 5 2 x + 25 4 = 0 x 2 + 3 2 x + 1 2 ± 1 2 x + 5 2 2 = 0

x 2 + 3 2 x + 1 2 + 1 2 x + 5 2 = 0 или x 2 + 3 2 x + 1 2 — 1 2 x — 5 2 = 0

x 2 + 2 x + 3 = 0 или x 2 + x — 2 = 0

Корнями первого уравнения будут x = — 1 ± i · 2 , корнями второго х = 1 и х = — 2 .

Ответ: x 1 , 2 = — 1 ± i 2 , x 3 = 1 , x 4 = — 2 .

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Решение квадратных уравнений с помощью комплексных чисел

Одна из причин введения комплексных чисел состояла в том, чтобы добиться разрешимости любого квадратного уравнения, в частности уравнения x2 = – 1.

Покажем, что расширив поле действительных чисел до поля комплексных чисел, мы получили поле, в котором каждое квадратное уравнение разрешимо, т.е. имеет решение. Так, уравнение x2 = – 1 имеет два решения: x1 = i, x2 = – i.

Это нетрудно установить проверкой: , .

Перейдем теперь к вопросу о решении полного квадратного уравнения. Квадратным уравнением называют уравнение вида:

где x – неизвестная, a, b, c – действительные числа, соответственно первый, второй коэффициенты и свободный член, причем . Решим это уравнение, выполнив над ним ряд несложных преобразований.

Разделим все члены уравнения на и перенесем свободный член в правую часть уравнения:

К обеим частям уравнения прибавим выражение с тем, чтобы левая его часть представляла полный квадрат суммы двух слагаемых:

Извлечем корень квадратный из обеих частей уравнения:

Найдем значения неизвестной:

Теперь можно исследовать полученное решение. Оно зависит от значения подкоренного выражения, называемого дискриминантом квадратного уравнения.

Если , то есть действительное число и квадратное уравнение имеет действительные корни.

Если же то мнимое число, квадратное уравнение имеет мнимые корни.

Результаты исследования представлены ниже в таблице:

Итак, введение комплексных чисел позволяет разработать полную теорию квадратных уравнений. В поле комплексных чисел разрешимо любое квадратное уравнение.

1. Решите уравнение .

Решение. Найдем дискриминант .

Уравнение имеет два действительных корня:

2. Решите уравнение .

Решение. , уравнение имеет два равных действительных корня:

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Двучленным называется уравнение вида $x^ =A$.

Рассмотрим три случая:

Решить уравнение: $x^ =8$.

Так как $A>0$, то $x_ =sqrt[ ] cdot left(cos frac +icdot sin frac
ight),, , , k=0. 2$.

При $k=0$ получаем $x_ =sqrt[ ] cdot left(cos 0+icdot sin 0
ight)=sqrt[ ] =2$.

При $k=1$ получаем

[x_ =sqrt[ ] cdot left(cos frac +icdot sin frac
ight)=sqrt[ ] cdot (-frac +frac > cdot i)=2cdot (-frac +frac > cdot i)=-1+sqrt cdot i.]

При $k=2$ получаем

[x_ =sqrt[ ] cdot left(cos frac +icdot sin frac
ight)=sqrt[ ] cdot (-frac -frac > cdot i)=2cdot (-frac -frac > cdot i)=-1-sqrt cdot i.]

Попробуй обратиться за помощью к преподавателям

Решить уравнение: $x^ =1+i$.

Так как $A$ – комплексное число, то

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа:

[varphi =arg z=arctgfrac =arctg1=frac

Подставим полученные значения и получим:

Уравнение перепишем в виде:

При $k=0$ получаем $x_ =sqrt[ ] > cdot left(cos frac

ight)=sqrt[ ] > cdot left(cos frac

ight)=sqrt[ ] cdot left(cos frac

При $k=1$ получаем

При $k=2$ получаем

Задай вопрос специалистам и получи
ответ уже через 15 минут!

Квадратным называется уравнение вида $ax^ +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^ -4ac$, при этом

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

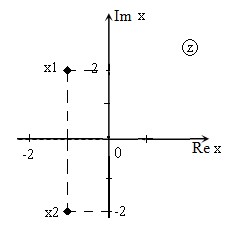
Решить уравнение $x^ +2x+5=0$ и изобразить корни на плоскости.

[D=2^ -4cdot 1cdot 5=4-20=-16.]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Комплексное число вида $overline =a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Известно, что если $x_ $ являются корнями квадратного уравнения $ax^ +bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ )(x-x_ )=0$. В общем случае $x_ $ являются комплексными корнями.

Зная корни уравнения $x_ =1pm 2i$, записать исходное уравнение.

Запишем уравнение следующим образом:

[x^ -(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0] [x^ -x+2icdot x-x-2icdot x+1-4i^ =0] [x^ -2x+1+4=0] [x^ -2x+5=0]

Следовательно, $x^ -2x+5=0$ – искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Решить уравнение: $z^ +(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.

Так как $D>0$, уравнение имеет два корня:

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

Так и не нашли ответ
на свой вопрос?

Просто напиши с чем тебе
нужна помощь

Устанавливая рекомендуемое программное обеспечение вы соглашаетесь
с лицензионным соглашением Яндекс.Браузера и настольного ПО Яндекса .

Урок на тему: «Решение квадратных уравнений с помощью комплексных чисел».

Образовательные: расширить понятие числа, ввести понятие комплексного числа, действия над комплексными числами, заданными в алгебраической форме.

Воспитательные: прививать интерес к математике, ознакомить учащихся с историей развития комплексных чисел, воспитывать

Развивающие : развивать творческое мышление, пространственное мышление, научить применять теоретические знания при решении практических задач, формировать активность и самостоятельность при работе в группах.

Используемые технологии и методы: 1) проблемный диалог; 2) информационно- коммуникационные технологии.

Тип занятия: комбинированный.

Повторение материала предыдущего занятия.

Изучение нового материала.

Закрепление нового материала.

1.Организационный момент (2 мин).

2. Повторение материала предыдущего занятия (10 мин).

Множество действительных чисел;

Множество комплексных чисел;

Определение и форма записи комплексного числа;

Изображение комплексного числа на комплексной оси;

Степени мнимой единицы;

3. Изучение нового материала.

-Как называется картинка, которую вы видите на экране? (Мем).

-Что мы знаем об извлечении корня из отрицательных чисел? (что корень из отрицательных чисел не извлекается).

-А что, если я докажу вам сегодня на уроке, что не так уж этот корень и нереален? А помогут мне в этом числа, с которыми мы познакомились на предыдущем занятии – комплексные числа!

Верно, что во множестве действительных чисел корней из отрицательных чисел быть не может. Об этом нам всем говорили в школе. НО, введение понятия «комплексное число» продвинуло вперед современную математику, а с ней и другие естественные науки.

Так вот, в множестве комплексных чисел корень из -1 извлекается и очень хорошо! Вспомним знакомую нам формулу . Корень из -1= i,

Исследование алгебраических уравнений является одним из важнейших вопросов в математике. Например, действительных корней не имеет квадратное уравнение с отрицательным дискриминантом. Простейшим таким уравнением является уравнение

Для того чтобы это уравнение имело решение, необходимо расширить множество действительных чисел путем присоединения к нему корня уравнения

Обозначим этот корень через . Таким образом, по определению

, или

Таким образом, действительных чисел явно недостаточно, чтобы построить такую теорию квадратных уравнений, в рамках которой каждое квадратное уравнение было бы разрешимо. Это приводит к необходимости расширять множество действительных чисел до множества, в котором было бы разрешимо любое квадратное уравнение. Такое множество называется множеством комплексных чисел и обозначается С.

Рассматривать будем на таком примере:

Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:

Выполним проверку того, что эти корни и права оказываются решением уравнения:

Что и требовалось доказать.

Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: .

Такие корни являются сопряженными комплексными корнями .

Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:

, ,

Решим квадратное уравнение .

Первым шагом определим дискриминант уравнения:

В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:

Как известно из формул дискриминанта у нас образуется 2 корня:

– сопряженные комплексные корни

Т.о., у уравнения есть 2 сопряженных комплексных корня:

Найти корни квадратного уравнения

Решение : на первом месте расположена мнимая единица, и, в принципе, от неё можно избавиться (умножая обе части на ) , однако, в этом нет особой надобности.

Для удобства выпишем коэффициенты:

Не теряем «минус» у свободного члена. Уравнение в стандартном виде :

Вычислим дискриминант:

А вот и главное препятствие:

Применение общей формулы извлечения корня осложняется серьёзными затруднениями, связанными с аргументом подкоренного комплексного числа (убедитесь сами) . Но существует и другой, «алгебраический» путь! Корень будем искать в виде:

Возведём обе части в квадрат:

Два комплексных числа равны, если равны их действительные и их мнимые части. Таким образом, получаем следующую систему:

Систему проще решить подбором (более основательный путь – выразить из 2-го уравнения – подставить в 1-е, получить и решить биквадратное уравнение) . Из 1-го уравнения следуют, что «икс» по модулю больше, чем «игрек». Кроме того, положительное произведение сообщает нам, что неизвестные одного знака. Исходя из вышесказанного, и ориентируясь на 2-е уравнение, запишем все подходящие ему пары: