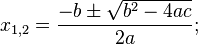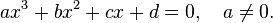Решение биквадратного уравнения на c

Выражение вида f(x)=0 называется уравнением. Число х называется корнем уравнения, если при его подстановке уравнение обращается в верное равенство. В статье рассмотрим методы решения уравнений — как точных, так и численных (приближенных).

Видео:Биквадратные уравнения. 8 класс алгебра.Скачать

Решение квадратных уравнений

Квадратным уравнением называется уравнение вида

Классическая формула для нахождения его корней (действительных и комплексных):

где выражение D = b 2 − 4ac называется дискриминантом уравнения, от его значения зависит количество и характер решений:

• Если D>0, то корней уравнения будет два и оба они будут действительными числами;
• Если D=0, то будет лишь один дейсвительный корень уравнения;
• Если D 2 +10x+200=0; данное уравнение не имеет действительных корней, но имеет пару сопряженных комплексных корней: x₁ = -1-6,2449979983984i, x₂ = -1+6,2449979983984i;
• x 2 -8x+16=0; данное уравнение имеет один двукратный корень x₁=x₂=4;
• x 2 -5x+6=0; данное уравнение имеет два различных корня x₁=2, x₂=3.

Напишем программу для решения этих уравнений:

На выходе получим:

5x^2 — 10x + 200 = 0
x0 = (-1, -6,2449979983984)
x1 = (-1, 6,2449979983984)

x^2 — 8x + 16 = 0
x0 = (4, 0)
x1 = (4, 0)

x^2 — 5x + 6 = 0
x0 = (3, 0)
x1 = (2, 0)

Воспользуемся WolframAlpha для проверки значений:

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Решение кубических уравнений

Кубическим уравнением называется уравнение третьего порядка, которое имеет вид

Кубическое уравнение всегда имеет 3 корня, которые могут быть как вещественными, так и комплексными. Для решения кубических уравнений используется метод Виета-Кардано.

Формулы Кардано и Виета требуют применения специальных функций, и в том случае, когда требуется провести большую серию вычислений корней кубического уравнения с не слишком сильно меняющимися коэффициентами, более быстрым алгоритмом является использование метода Ньютона или других итерационных методов (с нахождением начального приближения по формулам Кардано-Виета), о которых мы поговорим дальше.

Рассмотрим в качестве примера следующие кубические уравнения:

• x^3 — 6x^2 + 11x — 6 = 0
• x^3 — 6x^2 + 11x + 6 = 0

Напишем программу для решения кубических уравнений с помощью метода Виета-Кардано:

Напишем программу для тестирования метода:

x^3 — 6x^2 + 11x — 6 = 0
x0 = (1, 0)
x1 = (3, 0)
x2 = (2, 0)

x^3 — 6x^2 + 11x + 6 = 0
x0 = (-0,434841368216901, 0)
x1 = (3,21742068410845, 1,85643189109788)
x2 = (3,21742068410845, -1,85643189109788)

Решим эти же уравнения с помощью WolframAlpha.

Видео:Задача 411. Квадратное уравнение. acmp.ru C++Скачать

Решение биквадратных уравнений

Биквадратное уравнение — уравнение четвёртой степени вида

где a,b,c — заданные комплексные числа и a != 0. Подстановкой y = x 2 сводится к квадратному уравнению относительно y. Такой переход от одной неизвестной величины к другой называется методом замены неизвестных.

Рассмотрим в качестве примера кубические уравнения:

• 5x^4 — 10x^2 + 200 = 0
• x^4 — 8x^2 + 16 = 0
• x^4 — 5x^2 + 6 = 0

Таким образом немного модифицируем первую функцию для решения биквадратных уравнений:

Напшем программу для тестирования метода:

На выходе получим такие результаты:

5x^4 — 10x^2 + 200 = 0
x0 = (1,63164875514566, -1,91370783040891)
x1 = (-1,63164875514566, 1,91370783040891)
x2 = (1,63164875514566, 1,91370783040891)
x3 = (-1,63164875514566, -1,91370783040891)

x^4 — 8x^2 + 16 = 0
x0 = (2, 0)
x1 = (-2, 0)
x2 = (2, 0)
x3 = (-2, 0)

x^4 — 5x^2 + 6 = 0
x0 = (1,73205080756888, 0)
x1 = (-1,73205080756888, 0)
x2 = (1,4142135623731, 0)
x3 = (-1,4142135623731, 0)

По ссылкам раз, два, три можно убедиться в правильности решений.

Видео:5 Лайфхаков Которые Помогут Решить Биквадратное УравнениеСкачать

Составить программу для решения биквадратного уравнения

Видео:Решение биквадратных уравнений. Практическая часть. 2ч. 8 класс.Скачать

Ответы и объяснения

Решение биквадратного уравнения на Паскале схоже с решением квадратного уравнения. Только следует ввести замену x^2 -> a. Как только найдем корни a, можно извлекать из них квадратные корни – это и будут решения уравнения x.

program sqrt1;
uses
crt;
var
x1, x2: real;
a, b, c, result: real;
D: real;
s:string;
label m1;
begin
clrscr;
m1: writeln(‘Программа решения биквадратного уравнения’);
write(‘Введите первый коэффициент: ‘);
readln(a);
write(‘Введите второй коэффициент: ‘);
readln(b);
write(‘Введите свободный член: ‘);
readln(c);
D:=b*b-4*a*c;

if D>0 then
begin
x1:=(-b+sqrt(D))/(2*a);
x2:=(-b-sqrt(D))/(2*a);
if x1>=0 then
begin
x1:=sqrt(x1);
writeln(‘Первый корень: ‘,x1:3:3);
end;
if x2>=0 then
begin
x2:=sqrt(x2);
writeln(‘Второй корень: ‘,x2:3:3);
end;
end;

if D=0 then
begin
x1:=-b/(2*a);
if x1>=0 then
begin
x1:=sqrt(x1);
writeln(‘Один корень: ‘,x1:3:3);
end;
end;

Довольно часто в пособиях по программированию встречаются задания по нахождению решений каких-нибудь математических уравнений. Задача нахождения корней квадратного уравнения — это довольно тривиальная задача, как и многие другие задачи. Решается она очень просто при помощи листа бумаги и ручки, но решение можно автоматизировать посредством написания прикладной программы и её использования. В этой статье мы напишем такую программу.

Алгоритм решения квадратного уравнения

Многие знают, что уравнение вида ax 2 + bx + c = 0 , где a не равно 0, называют квадратным уравнением.

Существуют различные способы решения квадратных уравнений, но мы рассмотрим решение через дискриминант.

Обозначается дискриминант буквой D . Из школьного курса знаем, что D = b 2 — 4ac .

Существует несколько условий:

• Если D > 0, то решение имеет 2 различных вещественных корня.
• Если D = 0, то оба вещественных корня равны.
• Если D

Вывод и ввод будет осуществляться с консоли, поэтому подключаем заголовок #include для вводавывода в консоли, #include для работы с математическими функциями и область using namespace std;

Просим пользователя ввести значения переменных и сохраняем каждое значение

Проверяем условие, если дискриминант больше или равен 0, то находим корни и выводим

в противном случае выводим сообщение

На этом всё, осталось скомпилировать, запустить и проверить. Запускаем и вводим данные, чтобы D был меньше 0

В этом случае D = 3*3 — 4*2*3 = -15, а это меньше 0, значит ответ программа дала верный.

Ответы тоже верны. Программа работает правильно.

Ниже представлен весь листинг программы для нахождения корней квадратного уравнения на C++

Для вас это может быть интересно:

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Программа для решения квадратных уравнений на C++ : 15 комментариев

Программировать так сложно…

1. Nicknixer Автор записи 15.10.2016

Не так сложно, как Вам кажется! Немного литературы, немного практики и смотреть на код решения такой задачи Вы будете по-другому.

Доброго времени суток! Помогите пожалуйста написать программу, которая считает сколько символов в ряде двумерного массива. То есть , например массив 5 на 5, сколько символов в 1 ряде, сколько во 2 и т.д.

Ответил вам по электронной почте

Критику принимаете? 🙂
Программа дырявая как сито.

Если число очень маленькое, но положительное, например 10^(-20) — у вас будет переполнение или типо того. Оператор > проверяет знак числа (это отдельный бит), а оператор == для дробных чисел не имеет смысла, т.к. в младших разрядах числа обычно находится какой-нибудь мусор, который при таком сравнении дает false.

x = ( -1*b + sqrt(b*b – 4*a*c) ) / (2 * a);
x = ( -1*b – sqrt(b*b – 4*a*c) ) / (2 * a);

Тут есть три вопроса:
1) зачем два раза вычислять одно и тоже (я про корень)
2) что делать если мне корни надо как-то использовать, а не просто вывести (тут есть проблема, ведь у меня то один корень — то два). Чтобы лучше понять в чем проблема — попробуйте вынести вычисление корней в отдельную функцию. У вас то вообще, если корень один — то их выведется все равно два, одинаковых.
3) в переменной «a» может быть ноль (или близкое к нулю число) — при этом мы получим деление на ноль (а точнее, переполнение).

Но это ведь еще не все. Что будет если и «a» и «b» равны нулю? — тебе надо рассмотреть два варианта — если c = 0 (условно, близко к нулю), то корней бесконечно много. А если c != 0, то корней нет.

Вообще, эта задача — прекрасный пример для юнит-тестирования и демонстрации принципов разработки через тестирование. Именно его я рассматривал в своей статье по теме тестирования: Юнит-тестирование. Пример. Boost Unit Test. Дело в том, что тут куча вариантов сделать ошибку, при этом их понимание приходит не сразу, т.е. школьник решая задачу напишет по формуле которой учили (ну и вот как у вас). А потом надо разбираться и смотреть как программа может сломаться, при этом разрабатывать тесты.

1. Николай Сергейчук Автор записи 09.02.2017

Принимаем 🙂
Согласен с вами во всём! Программу можно реализовать намного лучше, используя различные проверки и валидацию входных данных.
Однако, статья рассчитана на аудиторию, которая только начинает познавать программирование или делает лабораторную. 🙂 Чтобы людям легче было понять, реализация данной программы упрощена до невозможности. И, возможно, несправедливо было с моей стороны не предупредить их о возможных ошибках в работе программы, которые могут вскрыться позже, если подать на вход определенные значения.
Кстати, у вас интересная статья по тестированию!

Помогите решить в Dev C++
Sqrt x^2+1+sqrt|x|,x0

Здравствуйте, можете помочь с решением биквадратного и триквадратного уравнения?

#include
using namespace std;
int main()
b;
cout c;
D = pow(b, 2) — 4 * a * c;
cout

ну и? если даже тупо скопировать код и вставить его в cpp.sh , ничего не работает. поебота какая то этот с++

Уважаемая, Лена! Я, надеюсь, вы знаете, что код программы, написанной на языке программирования C++ нельзя тупо вставить в блокнот и сохранить под названием «cpp.sh»? Если не знали, то я, видимо, открыл для вас Америку!

помогите решить. заданы 3 перемены a.b.c записать вы радение на С
b,
b и а не равно != с

iconcerts где забыл
#include

Я ради интереса написал программу нахождения корней квадратного уравнения на С++, с выводом корней как в десятичном виде, так и в виде простой дроби (причём уже сокращённой), потому что выводя корни в десятичном виде программа их одновременно сокращает и округляет и 1/3 превращается в 0.333333 хотя на самом деле 0.333333 (3), то есть для проверки правильно ли нашёл корни ваш ребёнок, вы с получите что-то типа: X1= 0.285714; X2=0.214286, а на самом деле это будет X1=2/7; X2=3/14, кроме того, если корень из дискриминанта не получается целым числом, вы уже получите двойную неточность: сначала при извлечении корня программа отсечёт значение до 4-6 цифр после запятой с округлением, а затем сделает то же самое при делении числителя на знаменатель. Я и здесь сделал вывод корней в двух значениях: в десятичном и в виде выражения X1= (-b + sqrt(D))/(2*a); X2= (-b — sqrt(D))/(2*a), то есть выводится примерно вот так X1=-5+sqrt(21)/2; X2=-5-sqrt(21)/2 с одновременным разложением дискриминанта под корнем на множители, вынесением этих множителей из-под корня, если они выносятся нацело, их перемножением и дальнейшим сокращением. Вот, например, имеем a=3, b=15, c=3, при решении получаем D=189 программа выдаёт десятичные корни X1= -0.208712 и X2= -4.79129, а в виде выражения имеем: X1= -5+sqrt(21)/2, то есть первоначально получаем: X1= -15+sqrt(189)/6, -> 189=21*9 -> -15+3sqrt(21)/6 далее идёт сокращение на 3 и итог -5+sqrt(21)/2

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте как обрабатываются ваши данные комментариев.

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Решение квадратного уравнения

Уравнение вида a⋅x 2 + b⋅x + c = 0 — квадратное уравнение.

a, b, c — действительные числа, a ≠ 0.

Для того чтобы вычислить корни квадратного уравнения, нужно сначала найти дискриминант.

D = b 2 — 4⋅a⋅c;

• если D 0, то уравнение имеет два действительных корня:
  • x₁ = (-b + √D) / (2⋅a);
  • x₂ = (-b + √D) / (2⋅a).

📽️ Видео

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Решение квадратного уравнения на C# для консоли Windows в Visual Studio 2022Скачать

Алгебра 8 класс (Урок№28 - Решение квадратных уравнений вида ax2 + bx + c = 0.Формула корней кв.ур.)Скачать

С++ для начинающих Урок 8 - Решение квадратного уравненияСкачать

решение (поиск корней) квадратных уравнений c++Скачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Решение биквадратных уравнений. Практическая часть. 1ч. 8 класс.Скачать

Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать

Программирование на С++. Урок 13. Решение квадратного уравнения.Скачать

Математика| Разложение квадратного трехчлена на множители.Скачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать