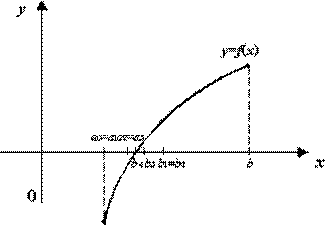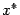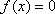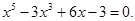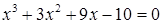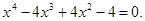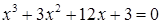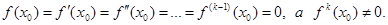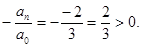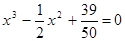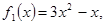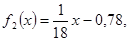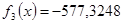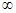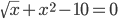Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций (2 видео)

Практическая работа 2.

26.03.2020

гр.753

ОТЧЁТ предоставить виде EXCEL документа по электронной почте или в Л/С ВК. не позднее 17:00

Содержание

Просмотр содержимого документа «Практическая работа 2.»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ — Тема: Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.
Лекция «Приближенные решения алгебраических и трансцендентных уравнений»
Метод половинного деления (метод дихотомии или метод бисекции)
📸 Видео

Просмотр содержимого документа
«Практическая работа 2.»

Практическая работа 2

Тема: Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.

Цель работы: изучить особенности различных методов решения алгебраических и трансцендентных уравнений методом половинного деления и методом итераций, приобрести навыки решения СЛАУ с помощью средств MS Excel выполнения задания

Ход выполнения практической работы:

Посмотреть видеоролик по теме «Методом половинного деления» перейдя по ссылке: https://youtu.be/ETb9qrU0Xls

Выполнить практическое задание:

Метод половинного деления (метод дихотомии)

Метод половинного деления основан на последовательном делении отрезка локализации корня пополам.

Для этого выбирается начальное приближение к отрезку [a, b], такое, что f(a)×f(b), затем определяется знак функции в точке 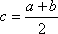— середине отрезка [a, b]. Если он противоположен знаку функции в точке a, то корень локализован на отрезке [a, c], если же нет – то на отрезке [c, b]. Схема метода дихотомии приведен на рисунке 2.

Рисунок 2. Последовательное деление отрезка пополам и приближение к корню

Алгоритм метода дихотомии можно записать так:

1. представить решаемое уравнение в виде

2. выбрать a, b и вычислить

3. если f(a)×f(с)то a=a; b = c иначе a = c; b=b

4. если критерий сходимости не выполнен, то перейти к п. 2

Пример решения уравнения методом дихотомии

Найти решение заданного уравнения методом дихотомии с точностью до 10 -5 .

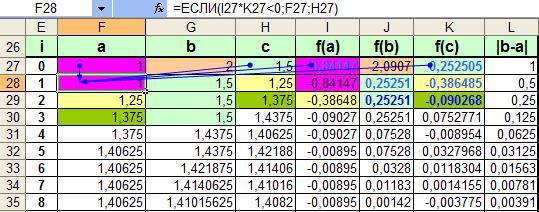
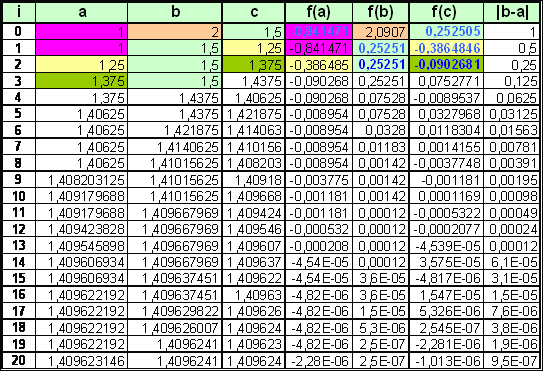
Пример создания расчетной схемы на основе метода дихотомии на примере уравнения: 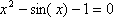на отрезке [1, 2]

Данный метод заключается в проверке на каждой итерации условия:

если f(a)×f(с) и выбор соответствующего отрезка для следующей итерации.

Рисунок 3. Последовательность итераций метода дихотомии при поиске корня уравнения 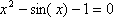на отрезке [1, 2]

Для нашего примера итерационная последовательность для нахождения решения принимает вид:

3. Выполненной задание прислать по эл.почте [email protected]

Видео:Метод половинного деления. ДихотомияСкачать

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ — Тема: Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.

— применить умения отделять корни алгебраических уравнений;

— применить умения решать алгебраические уравнений приближенными методами (метод половинного деления, метод хорд, метод касательных);

1. Рабочая тетрадь в клетку.

2. Раздаточный материал: инструкционные карты-20шт.

3. Калькулятор простой.

1. Методом половинного деления с точностью 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения

1. Методом итераций решить уравнение с точностью до 0,001

2. Методом итераций решить с точностью до 0,001 уравнение.

1. Внимательно прочитать тему и цель практической работы .

2. Изучить учебный материал по теме.

3. Ответить на вопросы.

4. Выполнить задания.

5. Подготовить отчет.

Пояснения к работе (учебный материал):

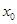
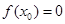
Число из области определения функции называется корнем уравнения , если .

Процесс нахождения корней уравнения распадается на несколько этапов:

1) определяются границы интервала, в котором находятся все корни уравнения ;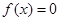

2) устанавливаются возможно малые промежутки, в каждом из которых содержатся ровно один корень.

3) каждый из корней вычисляется с заданной точностью.

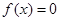
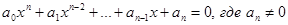
К сожалению, определение в общем виде границ интервала, в котором находятся все корни уравнения , можно дать только для алгебраического уравнения в каноническом виде, т.е. для уравнения вида:

(1)

В дальнейшем будем находить действительные корни алгебраических уравнений.

Теорема 1 (основная теорема алгебры).

Уравнения вида (1) имеет ровно n корней, действительных или комплексных, если корень кратности k считать за k корней.

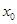
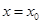
Число называется корнем кратности k уравнения (1), если при обращается в нуль сама функция и ее производные до ( k -1 )-го порядка включительно, т.е.

Корень кратности 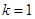называется простым.

1) Число действительных корней уравнения (1) четной степени с действительными коэффициентами всегда четно (в том числе и может равняться нулю).

Если кроме этого 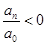, то уравнение четной степени имеет, по крайней мере, два действительных корня разного знака.

2) Уравнение (1) нечетной степени имеет по крайней мере один действительный корень того же знака, что и « ».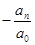

Теорема 3 (теорема Декарта).

Число положительных корней уравнения (1) равно или на четное число меньше числа перемен знака в ряду коэффициентов 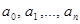уравнения. Так как при замене «х» на «-у» корни уравнения (1) меняют знаки, то с помощью этой теоремы можно оценить и число отрицательных корней.

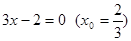
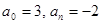
1. В уравнении нечетной степени коэффициенты и

Кроме этого, число перемен знаков равно 1.

Следовательно, по теоремам 2 и 3, оно имеет один действительный положительный корень.

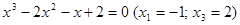
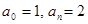
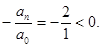
2. В уравнении нечетной степени коэффициенты и Следовательно по теореме 2, оно имеет по крайней мере один действительный отрицательный корень.

Число перемен знаков в данном уравнении равно двум, следовательно, по теореме 3, оно имеет либо два, либо 0 положительных действительных корней.

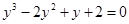
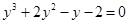
Оценим число действительных отрицательных корней. Для этого заменим «х» на «-у». Получим уравнение, или , или . Число перемен знаков в этом уравнении равно 1, следовательно, исходное уравнение имеет один действительный отрицательный корень.

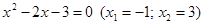
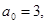
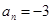
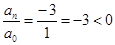
3. В уравнении четной степени коэффициенты и . Следовательно, по теореме 2, оно имеет два действительных корня разного знака.

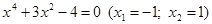
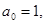
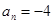
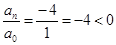
4. В уравнении четной степени коэффициенты и . Следовательно, по теореме 2, оно имеет по крайней мере два действительных корня разного знака.

Число перемен знаков в данном уравнении равно 1, следовательно, по теореме 3, оно имеет один положительный действительный корень.

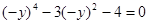
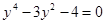
Оценим число действительных отрицательных корней. Для этого заменим «х» на «-у». Получим уравнение или . Число перемен знаков в этом уравнении равно 1, следовательно, исходное уравнение имеет один действительный корень.

Дадим теперь формулировку теоремы, позволяющей достаточно грубо определять границы интервала, в котором находятся все действительные корни уравнения (1).

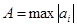
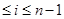
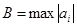
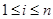
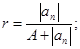
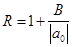
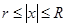
1) Если , где 0 ; , где , и , то .

2) Все положительные действительные корни уравнения находятся в промежутке , а все отрицательные действительные корни уравнения (1) находятся в промежутке .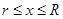

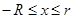
Если непрерывная и дифференцируемая функции , определяющая алгебраическое уравнение , на концах отрезка принимает значения разных знаков, т.е. , и ее первая производная сохраняет знак внутри этого отрезка, но на находится ровно один действительный корень данного уравнения.

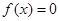
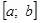
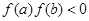
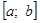
Замечание. Для алгебраических уравнений (1), степень которых больше трех, трудно аналитически находить интервалы знакопостоянства функции . Поэтому для нахождения возможно малых промежутков, содержащих ровно один действительный корень можно на практике использовать следующие способы:

1) средствами машинной графики функция представляется на дисплее и приближенно определяются возможно малые промежутки, содержащие ровно один корень (т.е. промежутки содержащие одну точку пересечения графика функции с осью Ох);

2) если график функции построить трудно, то формируют простые функции и , такие, что уравнение преобразуется в виде = . Затем строятся графики функций у= и y = и приближенно определяются промежутки, содержащие абсциссы точек пересечения этих графиков.

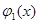
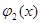
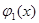
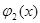
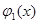
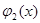
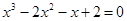
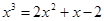
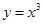
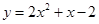
Так, например, уравнение можно преобразовать к виду и затем построить графики функции и .

Начиная третий этап, дадим формулировку теоремы, позволяющей оценивать погрешность приближенного решения.

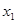
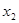
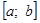
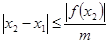
Если точный, а — приближенный, корни уравнения (1), принадлежащие одному и тому же промежутку , то справедливая оценка: , где m – наименьшее значение модуля производной функции на промежутке .

Графически решить уравнение x ln ( x )=1 .

Решение. Запишем исходное уравнение в виде: , т.е. и . Таким образом, корни данного уравнения могут быть найдены как абсциссы точек пересечения кривых и .

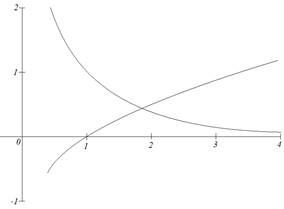
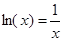
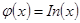
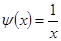
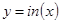
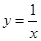
Теперь построим графики функций и определим интервал изоляции корня.

Аналитически отделить корни данного алгебраического уравнения, используя теорему Штурма:

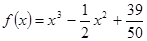
Построим таблицу для подсчета смены знаков:

—

Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Лекция «Приближенные решения алгебраических и трансцендентных уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Видеолекции для
профессионалов

Свидетельства для портфолио
Вечный доступ за 120 рублей
311 видеолекции для каждого

Раздел 2. Численные методы

1. Алгебраические и трансцендентные уравнения

2. Графический метод решения уравнений

1. Алгебраические и трансцендентные уравнения

При решении практических задач часто приходится сталкиваться с решением уравнений. Всякое уравнение с одним неизвестным можно представить в виде

( x )= g ( x ), (1)

где (х) и g (х) — данные функции, определенные на некотором числовом множестве X , называемом областью допустимых значений уравнения.

В общем случае нелинейное уравнение можно записать в виде:

где функция F ( x ) определена и непрерывна на конечном или бесконечном интервале .

? Совокупность значений переменной х, при которых уравнение (1) превращается в тождество, называется решением этого уравнения, а каждое значение х: из этой совокупности называется корнем уравнения.

? Всякое число , обращающее функцию F ( x ) в нуль, т.е. такое, при котором F ( )=0, называется корнем уравнения (1).

? Число называется корнем k -той кратности , если при x = вместе с функцией F ( x ) равны нулю ее производные до ( k -1) порядка включительно:

F ( ) = F / ( ) = … = F ( k -1) ( ) = 0.

Однократный корень называется простым.

? Решить уравнение – значит найти множество всех корней этого уравнения.

Оно может быть конечным или бесконечным.

? Два уравнения F ( x )=0 и G ( x =0) называются равносильными (эквивалентными), если всякое решение каждого из них является решением и для другого, то есть множества решений этих уравнений совпадают.

В зависимости от того, какие функции входят в уравнения (1) или (2), уравнения разделяются на два больших класса: линейные и нелинейные.

Нелинейные уравнения делятся, в свою очередь на: алгебраические и трансцендентные.

Уравнение (2) называется алгебраическим, если функция является алгебраической функцией. Путем алгебраических преобразований из всякого алгебраического уравнения можно получить уравнение в канонической форме:

где a ₀ , a ₁ , . , a_n — коэффициенты уравнения, а x -неизвестное. Показатель n называется степенью алгебраического уравнения.

Если функция F ( x ) не является алгебраической, то уравнение (1) называется трансцендентным.

В некоторых случаях решение трансцендентных уравнений можно свести к решению алгебраических уравнений.

Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций

Решение уравнения с одним неизвестным заключается в отыскании корней, т. е. тех значений х, которые обращают уравнение в тождество. Корни уравнения могут быть вещественными и невещественными (комплексными).

Найти точные значения корней уравнения можно только в исключительных случаях, обычно, когда есть какая-либо простая формула для вычисления значения корней, выражающая их через известные величины.

Поскольку подавляющее большинство нелинейных уравнений с одной переменой не решаются путем аналитических преобразований (точными методами), на практике их решают только численными методами.

При решении многих практических задач точное решение уравнения не всегда является необходимым. Задача нахождения корней считается решенной, если корни вычислены с заданной степенью точности.

? Решить уравнение – это значит

· установить, имеет ли оно корни,

· и найти значение корней с заданной точностью.

? Задача численного нахождения действительных и комплексных корней уравнения (2) обычно состоит из двух этапов:

1. отделение корней , т.е. нахождение достаточно малых окрестностей рассматриваемой области, в которых находится одно значение корня,

2. и уточнение корней, т.е. вычисление корней с заданной степенью точности в некоторой окрестности.

Наиболее распространенными на практике численными методами решения уравнения (2) являются: метод половинного деления, метод хорд, метод касательных (Ньютона), комбинированный метод, метод простой итерации. Применение того или иного метода для решения уравнения (2) зависит от числа корней, задания исходного приближения и поведения функции F ( x ).

2. Графические методы решения уравнений

Одним из методов решения уравнений является графический. Точность такого решения невелика, однако с помощью графика можно разумно выбрать первое приближение, с которого начнется дальнейшее решение уравнения. Существуют два способа графического решения уравнений.

Первый способ. Все члены уравнения переносят в левую часть, т. е. представляют его в виде f (х) = 0. После этого строят график функции у = f ( x ) , где f (х) – левая часть уравнения. Абсциссы точек пересечения графика функции у = f (х) с осью Ох и являются корнями уравнения, так как в этих точках у = 0 (рис. 1).

Рисунок 1

Второй способ. Все члены уравнения разбивают на две группы, одну из них записывают в левой части уравнения, а другую в правой, т. е. представляют его в виде f (х) = g (х).

После этого строят графики двух функций у = f (х) и у = g (х). Абсциссы точек пересечения графиков этих двух функций и служат корнями данного уравнения. Пусть точка пересечения графиков имеет абсциссу х₀, ординаты обоих графиков в этой точке равны между собой, т. е. f (х₀) = g (х₀). Из этого равенства следует, что х₀ – корень уравнения (рис. 2).

Рисунок 2

Пример 1. Решить графически уравнение х 3 — 2 x 2 + 2х — 1 = 0.

Первый способ. Построим график функции у = х 3 — 2 x 2 + 2х — 1 и определим абсциссы точек пересечения этого графика с осью Ох. Кривая пересекает ось Ох в точке х = 1, следовательно, уравнение имеет один корень (рис. 3). (Отметим, что алгебраическое уравнение третьей степени имеет или один действительный корень или три. Так как кривая пересекает ось абсцисс только в одной точке, то данное уравнение имеет только один действительный корень. Остальные два корня – комплексные.)

Рисунок 3 Рисунок 4

Второй способ. Представим данное уравнение в виде х 3 = 2 x 2 + 2х–1 и построим графики функций у = х 3 и у = 2 x 2 + 2х – 1. Найдем абсциссу точки пересечения этих графиков; получим х = 1 (рис. 4).

Пример 2. Найти приближенно графическим способом корни уравнения lg х — Зх + 5 = 0.

Перепишем уравнение следующим образом: lg х = Зх — 5.

Функции в левой и в правой части уравнения имеют общую область определения: интервал 0 . Поэтому будем искать корни именно в этом интервале.

Строим графики функций у = lg х и у = Зх — 5 (рис. 5). Прямая у = Зх-5 пересекает логарифмическую кривую в двух точках с абсциссами x₁0,00001 и x₂1,75. На рисунке трудно показать пересечение графиков этих двух функций в первой точке, однако, учитывая, что нижняя ветвь, логарифмической кривой неограниченно приближается к оси Оу, можно предполагать, что пересечение этих двух графиков произойдет вблизи точки пересечения графика функции у = Зх — 5 и оси Оу. Абсцисса точки пересечения приближенно равна 0,00001. Итак, корни уравнения x₁0,00001 и x₂1,75

Рисунок 5 Рисунок 6

Пример 3. Найти графически корни уравнения 2 х = 2х.

Решение. Строим графики функций у = 2 х и у = 2х. Эти графики пересекаются в двух точках, абсциссы которых равны х₁ = 1 и х₂ = 2. Данное уравнение имеет два корня х₁= 1 и х₂ = 2 (рис. 6).

Подводя итог вышеизложенному, можно рекомендовать для графического решения уравнения f (х) = 0 , все корни которого лежат в промежутке [а, b ], следующую простую схему.

1. Представить указанное уравнение в виде (х) = g (х) с таким расчетом, чтобы функции у= (х) и у = g (х) были просты и удобны для исследования и построения.

2. На бумаге вычертить графики функций у = (х) и у = g (х) в промежутке [а, b ].

3. Если графики не пересекаются, то корней в данном промежутке нет. Если же графики пересекаются, то нужно определить точки их пересечения, найти абсциссы этих точек, которые и будут приближенными значениями корней рассматриваемого уравнения.

Первый этап численного решения уравнения (2) состоит в отделении корней, т.е. в установлении “тесных” промежутков, содержащих только один корень.

? Корень уравнения f (х) = 0 считается отделенным на отрезке [ a , b ] , если на этом отрезке уравнение f (х) = 0 не имеет других корней.

? Отделить корни – это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень.

Отделение корней можно произвести двумя способами – графическим и аналитическим.

Графический метод отделения корней. При графическом методе отделения корней поступают так же, как и при графическом методе решения уравнений.

Графический метод отделения корней не обладает большой точностью. Он дает возможность грубо определить интервалы изоляции к орня. Далее корни уточняются одним из способов, указанных ниже.

Аналитический метод отделения корней. Аналитически корни уравнения f(х) =0 можно отделить, используя некоторые свойства функций, изучаемые в курсе математического анализа.

Сформулируем без доказательства теоремы, знание которых необходимо при отделении корней.

1) Если непрерывная на отрезке функция F ( x ) принимает на его концах значения разных знаков, то уравнение (2) имеет на этом отрезке, по меньшей мере, один корень

2) Если функция F ( x ) к тому же еще и строго монотонна, то корень на отрезке единственный.

Рассмотрим примеры поведения некоторых функций:

Рисунок 7

Для отделения корней можно эффективно использовать ЭВМ.

Пусть имеется уравнение F ( x )=0, причем можно считать, что все корни находятся на отрезке , в которой функция F ( x ) отделена, непрерывна и F ( A )* F ( B ) , содержат не по одному корню.

Будем вычислять значения F ( x ), начиная с точки X = A , двигаясь вправо с некоторым шагом h .

Как только обнаружится пара соседних значений F ( x ), имеющих разные знаки, и функция F ( x ) монотонна на этом отрезке, так соответствующие значения аргумента X (предыдущее и последующее) можно считать концами отрезка, содержащего корень.

Схема соответствующего алгоритма изображена ниже. Результатом решения поставленной задачи будут выводимые на дисплей в цикле значения параметров X ₁ и X ₂ (Концов выделенных отрезков).

Видео:Метод половинного деления решение нелинейного уравненияСкачать

Метод половинного деления (метод дихотомии или метод бисекции)

Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξ_i являющихся приближением корня на i -ом шаге.
ξ_i=½(b_i+a_i), i=0,1.
где a₀=a; b₀=b; a_i;b_i — границы подынтервалов, в которых f(a_i)f(b_i) 0 мы ни задали, всегда можно найти такое n , что ч.т.д.
Графически метод дихотомии выглядит следующим образом

|f(c)|≤δ f(a)f(c) 10 = 1024 ≈ 10 3 раз. За 20 итераций (n=2) уменьшается в 2 20 ≈ 10 6 раз.

Пример №1 . Найти экстремум функции: y=5x 2 -4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].

Решение
Видео решение

Пример №3 . Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10 -2 . Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10 -4 . Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x 2 = 10, a = 2.6, b = 3

Найдем корни уравнения:
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /₂(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /₂ n (b-a)
В качестве корня ξ. возьмем 1 /₂(a_n+b_n). Тогда погрешность определения корня будет равна (b_n – a_n)/2. Если выполняется условие:
(b_n – a_n)/2 1 /₂(a_n+b_n).
Решение.
Поскольку F(2.6)*F(3) 0, то a=2.8
Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) 0, то a=2.825
Остальные расчеты сведем в таблицу.

N	c	a	b	f(c)	f(x)
1	2.6	3	2.8	-1.6275	-0.4867
2	2.8	3	2.9	-0.4867	0.1129
3	2.8	2.9	2.85	0.1129	-0.1893
4	2.8	2.85	2.825	-0.1893	-0.3386
5	2.825	2.85	2.8375	-0.3386	-0.2641
6	2.8375	2.85	2.8438	-0.2641	-0.2267

Ответ: x = 2.8438; F(x) = -0.2267
Решение было получено и оформлено с помощью сервиса Метод Ньютона онлайн

Пример №2 . Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε₁ = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε₂ = 0,0001. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε₂ число итераций.