Графическая интерпретация метода представлена на рис.3.5. Предположим, что каким-либо способом найдено начальное приближение х0 к истинному корню. Например, при использовании отделения корней, в качестве х0 можно взять левую или правую границу промежутка, содержащего корень уравнения F(x) = 0, либо любую другую точку из этого промежутка. В точке х0 вычислим значение функции F(x), а также значение ее производной F ‘ (x). Следующее приближение к корню, т.е. точку х1 определим, как пересечение оси ОХ с касательной к кривой F(x) в точке х0:
Аналогичным образом, вычислив значения F(x) и F ‘ (x), в точке х1, можно получить приближение х2:
В общем случае вычислительный процесс метода Ньютона выражается формулой:
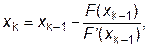 | (3.6) |
где каждое новое значение хk (k=1, 2, 3, …) будет располагаться все ближе к истинному корню х*., т.е. будет представлять собой все более точное приближение к решению уравнения F(x) = 0.
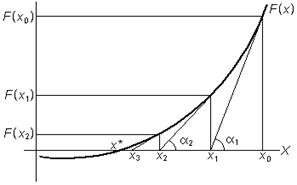 Рис.3.5. Метод Ньютона Рис.3.5. Метод Ньютона | 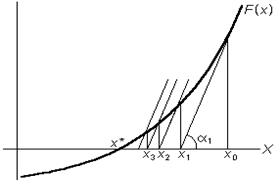 Рис.3.6. Модифицированный метод Ньютона Рис.3.6. Модифицированный метод Ньютона |
Процесс уточнения корня по формуле (3.6) следует прекращать, когда выполнится условие 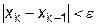
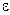
Метод Ньютона обладает высокой скоростью сходимости. Обычно абсолютная точность решения 10 -5 – 10 -6 достигается за 4-5 итераций. Недостатком метода является необходимость вычисления на каждом шаге не только левой части F(x) уравнения, но и ее первой производной.
На практике иногда применяется так называемый модифицированный метод Ньютона, который отличается от метода Ньютона тем, что первая производная от F(x) вычисляется лишь один раз в точке х0. Вычислительный процесс модифицированного метода Ньютона описывается формулой:
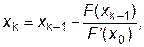 | (3.7) |
а его геометрическая иллюстрация приведена на рис. 3.6.
Видео:Численное решение уравнений, урок 5/5. Комбинированный метод хорд и касательныхСкачать

Метод Ньютона
Инструкция . Введите выражение F(x) , нажмите Далее . Полученное решение сохраняется в файле Word . Также создается шаблон решения в Excel .
- Решение онлайн
- Видеоинструкция
- Оформление Word
Правила ввода функции, заданной в явном виде
- Примеры правильного написания F(x) :
- 10•x•e 2x = 10*x*exp(2*x)
- x•e -x +cos(3x) = x*exp(-x)+cos(3*x)
- x 3 -x 2 +3 = x^3-x^2+3
- Выражение 0.9*x=sin(x)+1 необходимо преобразовать к виду: sin(x)+1-0.9*x . Аналогично, x^2-7=5-3x к виду x^2+3x-12 .
Пусть дано уравнение f(x)=0 , где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b . Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x) . Число ξ называется корнем k -ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)= … =f k-1 (ξ) = 0 . Однократный корень называется простым.
Приближенное нахождение корней уравнения складывается из двух этапов:- Отделение корней, то есть установление интервалов [αi,βi] , в которых содержится один корень уравнения.
- f(a)•f(b) , т.е. значения функции на его концах имеют противоположные знаки.
- f’(x) сохраняет постоянный знак, т.е. функция монотонна (эти два условия достаточны, но НЕ необходимы) для единственности корня на искомом отрезке).
- f”(x) сохраняет постоянный знак, т.е. функция выпукла вверх, либо – вниз.
- Уточнение приближенных корней, то есть доведение их до заданной точности.
Видео:Метод касательных (метод Ньютона)Скачать
Геометрическая интерпретация метода Ньютона (метод касательных)
Критерий завершения итерационного процесса имеет вид
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать
Лекция «Приближенные решения алгебраических и трансцендентных уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
БИК Курс лекций по дисциплине «Численные методы»
для специальности 230105 Программное обеспечение вычислительной техники и автоматизированных систем
Раздел 2. Численные методы
2.1.1. Приближенные решения алгебраических и трансцендентных уравнений
Алгебраические и трансцендентные уравнения
Графический метод решения уравнений
1. Алгебраические и трансцендентные уравнения
При решении практических задач часто приходится сталкиваться с решением уравнений. Всякое уравнение с одним неизвестным можно представить в виде
( x )= g ( x ), (1)
где
(х) и g (х) — данные функции, определенные на некотором числовом множестве X , называемом областью допустимых значений уравнения .
В общем случае нелинейное уравнение можно записать в виде:
F ( x ) определена и непрерывна на конечном или бесконечном интервале
.
Совокупность значений переменной х, при которых уравнение (1) превращается в тождество, называется решением этого уравнения, а каждое значение х : из этой совокупности называется корнем уравнения.
Всякое число
, обращающее функцию F ( x ) в нуль, т.е. такое, при котором F (
)=0, называется корнем уравнения (1).
Число
называется корнем k -той кратности, если при x =
вместе с функцией F ( x ) равны нулю ее производные до ( k -1) порядка включительно:
F (
) = F / (
) = … = F ( k -1) (
) = 0.
Однократный корень называется простым.
Решить уравнение – значит найти множество всех корней этого уравнения.
Оно может быть конечным или бесконечным.
Два уравнения F ( x )=0 и G ( x =0) называются равносильными (эквивалентными), если всякое решение каждого из них является решением и для другого, то есть множества решений этих уравнений совпадают.
В зависимости от того, какие функции входят в уравнения (1) или (2), уравнения разделяются на два больших класса: линейные и нелинейные.
Нелинейные уравнения делятся, в свою очередь на: алгебраические и трансцендентные .
Уравнение (2) называется алгебраическим, если функция является алгебраической функцией. Путем алгебраических преобразований из всякого алгебраического уравнения можно получить уравнение в канонической форме:
где a 0, a 1, . , a n — коэффициенты уравнения, а x -неизвестное. Показатель n называется степенью алгебраического уравнения.
Если функция F ( x ) не является алгебраической, то уравнение (1) называется трансцендентным.
В некоторых случаях решение трансцендентных уравнений можно свести к решению алгебраических уравнений.
Решение уравнения с одним неизвестным заключается в отыскании корней, т. е. тех значений х, которые обращают уравнение в тождество. Корни уравнения могут быть вещественными и невещественными (комплексными).
Найти точные значения корней уравнения можно только в исключительных случаях, обычно, когда есть какая-либо простая формула для вычисления значения корней, выражающая их через известные величины.
Поскольку подавляющее большинство нелинейных уравнений с одной переменой не решаются путем аналитических преобразований (точными методами), на практике их решают только численными методами.
При решении многих практических задач точное решение уравнения не всегда является необходимым. Задача нахождения корней считается решенной, если корни вычислены с заданной степенью точности.
Решить уравнение – это значит
установить, имеет ли оно корни,
и найти значение корней с заданной точностью.
Задача численного нахождения действительных и комплексных корней уравнения (2) обычно состоит из двух этапов:
отделение корней, т.е. нахождение достаточно малых окрестностей рассматриваемой области, в которых находится одно значение корня,
и уточнение корней, т.е. вычисление корней с заданной степенью точности в некоторой окрестности.
Наиболее распространенными на практике численными методами решения уравнения (2) являются: метод половинного деления, метод хорд, метод касательных (Ньютона), комбинированный метод, метод простой итерации. Применение того или иного метода для решения уравнения (2) зависит от числа корней, задания исходного приближения и поведения функции F ( x ).
2. Графические методы решения уравнений
Одним из методов решения уравнений является графический. Точность такого решения невелика, однако с помощью графика можно разумно выбрать первое приближение, с которого начнется дальнейшее решение уравнения. Существуют два способа графического решения уравнений.
Первый способ. Все члены уравнения переносят в левую часть, т. е. представляют его в виде f (х) = 0. После этого строят график функции у = f ( x ), где f (х) – левая часть уравнения. Абсциссы точек пересечения графика функции у = f (х) с осью Ох и являются корнями уравнения, так как в этих точках у = 0 (рис. 1).
Рисунок 1
Второй способ. Все члены уравнения разбивают на две группы, одну из них записывают в левой части уравнения, а другую в правой, т. е. представляют его в виде f (х) = g (х).
После этого строят графики двух функций у = f (х) и у = g (х). Абсциссы точек пересечения графиков этих двух функций и служат корнями данного уравнения. Пусть точка пересечения графиков имеет абсциссу х0, ординаты обоих графиков в этой точке равны между собой, т. е. f (х0) = g (х0). Из этого равенства следует, что х0 – корень уравнения (рис. 2).
Рисунок 2
Пример 1. Решить графически уравнение х 3 — 2 x 2 + 2х — 1 = 0.
Первый способ. Построим график функции у = х 3 — 2 x 2 + 2х — 1 и определим абсциссы точек пересечения этого графика с осью Ох. Кривая пересекает ось Ох в точке х = 1, следовательно, уравнение имеет один корень (рис. 3). (Отметим, что алгебраическое уравнение третьей степени имеет или один действительный корень или три. Так как кривая пересекает ось абсцисс только в одной точке, то данное уравнение имеет только один действительный корень. Остальные два корня – комплексные.)
Рисунок 3
Рисунок 4
Второй способ. Представим данное уравнение в виде х 3 = 2 x 2 + 2х–1 и построим графики функций у = х 3 и у = 2 x 2 + 2х – 1. Найдем абсциссу точки пересечения этих графиков; получим х = 1 (рис. 4).
Пример 2. Найти приближенно графическим способом корни уравнения lg х — Зх + 5 = 0.
Перепишем уравнение следующим образом: lg х = Зх — 5.
Функции в левой и в правой части уравнения имеют общую область определения: интервал 0
Строим графики функций у = lg х и у = Зх — 5 (рис. 5). Прямая у = Зх-5 пересекает логарифмическую кривую в двух точках с абсциссами x 1
0,00001 и x 2
1,75. На рисунке трудно показать пересечение графиков этих двух функций в первой точке, однако, учитывая, что нижняя ветвь, логарифмической кривой неограниченно приближается к оси Оу, можно предполагать, что пересечение этих двух графиков произойдет вблизи точки пересечения графика функции у = Зх — 5 и оси Оу. Абсцисса точки пересечения приближенно равна 0,00001. Итак, корни уравнения x 1
0,00001 и x 2
1,75
Рисунок 5
Рисунок 6
Пример 3. Найти графически корни уравнения 2 х = 2х.
Решение. Строим графики функций у = 2 х и у = 2х. Эти графики пересекаются в двух точках, абсциссы которых равны х 1 = 1 и х 2 = 2. Данное уравнение имеет два корня х 1 = 1 и х 2 = 2 (рис. 6).
Подводя итог вышеизложенному, можно рекомендовать для графического решения уравнения f (х) = 0, все корни которого лежат в промежутке [а, b ], следующую простую схему.
1. Представить указанное уравнение в виде
(х) = g (х) с таким расчетом, чтобы функции у=
(х) и у = g (х) были просты и удобны для исследования и построения.
2. На бумаге вычертить графики функций у =
(х) и у = g (х) в промежутке [а, b ].
3. Если графики не пересекаются, то корней в данном промежутке нет. Если же графики пересекаются, то нужно определить точки их пересечения, найти абсциссы этих точек, которые и будут приближенными значениями корней рассматриваемого уравнения.
Первый этап численного решения уравнения (2) состоит в отделении корней, т.е. в установлении “тесных” промежутков, содержащих только один корень.
Корень
уравнения f (х) = 0 считается отделенным на отрезке [ a , b ] , если на этом отрезке уравнение f (х) = 0 не имеет других корней.
Отделить корни – это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень.
Отделение корней можно произвести двумя способами – графическим и аналитическим.
Графический метод отделения корней. При графическом методе отделения корней поступают так же, как и при графическом методе решения уравнений.
Графический метод отделения корней не обладает большой точностью. Он дает возможность грубо определить интервалы изоляции к орня. Далее корни уточняются одним из способов, указанных ниже.
Аналитический метод отделения корней. Аналитически корни уравнения f(х) =0 можно отделить, используя некоторые свойства функций, изучаемые в курсе математического анализа.
Сформулируем без доказательства теоремы, знание которых необходимо при отделении корней.
1) Если непрерывная на отрезке
функция F ( x ) принимает на его концах значения разных знаков, то уравнение (2) имеет на этом отрезке, по меньшей мере, один корень
2) Если функция F ( x ) к тому же еще и строго монотонна, то корень на отрезке
единственный.
Рассмотрим примеры поведения некоторых функций:
Рисунок 7
Для отделения корней можно эффективно использовать ЭВМ.
П
усть имеется уравнение F ( x )=0, причем можно считать, что все корни находятся на отрезке
, в которой функция F ( x ) отделена, непрерывна и F ( A )* F ( B ) F ( x ), начиная с точки X = A , двигаясь вправо с некоторым шагом h .
Как только обнаружится пара соседних значений F ( x ), имеющих разные знаки, и функция F ( x ) монотонна на этом отрезке, так соответствующие значения аргумента X (предыдущее и последующее) можно считать концами отрезка, содержащего корень.
Схема соответствующего алгоритма изображена ниже. Результатом решения поставленной задачи будут выводимые на дисплей в цикле значения параметров X 1 и X 2 (Концов выделенных отрезков).
💡 Видео
Метод простых итераций пример решения нелинейных уравненийСкачать
Метод Касательных - ВизуализацияСкачать
Метод Хорд - ВизуализацияСкачать
Численное решение уравнений, урок 4/5. Метод касательных (Ньютона)Скачать
15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать
Метод хорд для приближённого решения алгебраических уравненийСкачать
Численное решение уравнений, урок 3/5. Метод хордСкачать
Химические уравнения 8, 9 класс || Задание 7.1. ВПР по химииСкачать
Как распознать талантливого математикаСкачать
1 4 Метод Ньютона касательныхСкачать
Метод касательныхСкачать
11 Метод Ньютона (Метод касательных) Mathcad Численные методы решения нелинейного уравненияСкачать
Вычислительная математика. Метод касательных на Python(1 практика).Скачать
10 Численные методы решения нелинейных уравненийСкачать
Решение нелинейного уравнения методом Ньютона (касательных) (программа)Скачать
1 3 Решение нелинейных уравнений методом простых итерацийСкачать
10 Метод Ньютона (Метод касательных) C++ Численные методы решения нелинейного уравненияСкачать
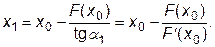
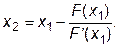


 ( x )= g ( x ), (1)
( x )= g ( x ), (1) .
. , обращающее функцию F ( x ) в нуль, т.е. такое, при котором F (
, обращающее функцию F ( x ) в нуль, т.е. такое, при котором F (  )=0, называется корнем уравнения (1).
)=0, называется корнем уравнения (1).
 Рисунок 1
Рисунок 1 Рисунок 2
Рисунок 2 Рисунок 3
Рисунок 3  Рисунок 4
Рисунок 4 0,00001 и x 2
0,00001 и x 2  Рисунок 5
Рисунок 5  Рисунок 6
Рисунок 6 функция F ( x ) принимает на его концах значения разных знаков, то уравнение (2) имеет на этом отрезке, по меньшей мере, один корень
функция F ( x ) принимает на его концах значения разных знаков, то уравнение (2) имеет на этом отрезке, по меньшей мере, один корень
 Рисунок 7
Рисунок 7 усть имеется уравнение F ( x )=0, причем можно считать, что все корни находятся на отрезке
усть имеется уравнение F ( x )=0, причем можно считать, что все корни находятся на отрезке  , в которой функция F ( x ) отделена, непрерывна и F ( A )* F ( B ) F ( x ), начиная с точки X = A , двигаясь вправо с некоторым шагом h .
, в которой функция F ( x ) отделена, непрерывна и F ( A )* F ( B ) F ( x ), начиная с точки X = A , двигаясь вправо с некоторым шагом h .















