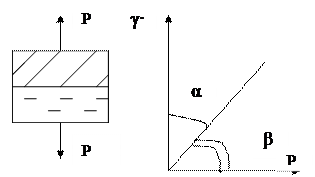
Реологическое уравнение состояния модели ньютона (4 видео)

Идеальные модели реологии. Модели Гука, Ньютона, Сен-Венана-Кулона.

Идеально упругое тело Гука представляется

в виде пружины с модулем Е. Р=Еγ –

деформация в пружине пропорциональна

напряжению. Особенность: полная механическая

и термодинамическая обратимость.

tg α = Е – модуль упругости (Юнга)

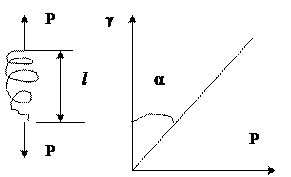
Идеально вязкое тело Ньютона: линейная

зависимость между напряжением сдвига (Р) и

скоростью деформации (γ). Перфорированный

поршень в вязкой среде. Коэф-т

пропорциональности называется вязкостью [Па · с]

или [Н · с/м 2 ]. Полностью механически и

tg α = η – вязкость (сопротивление с-мы

β – текучесть с-мы (диссипативная система)

Идеально пластическое тело Сен-Венана-Кулона.

Отсутствует пропорциональность между воздействием и

деформацией. Диссипативная с-ма, т.е. затраченная энергия

переходит в теплоту.

P>P_T γ>0 γ>0 — деформация происходит беспредельно

с любой скоростью. (Р_Т — предел текучести)

Принципы моделирования реологических свойств. Модель упругого тела Максвелла, Вывод уравнения, являющегося его математической моделью.

При последовательном соединении элементов, напряжения (Р=Р₁+Р₂=…=Р_n) будут равны, деформации и скорости деформации будут суммироваться. (γ= γ₁+γ₂+…+ γ_n ; γ= γ·₁+ γ·₂+…+ γ·_n)

При параллельном соединении элементов – напряжения будут суммироваться (Р=Р₁+Р₂+…+Р_n), деформации и скорости деформации будут равны (γ= γ₁=γ₂=…= γ_n ; γ= γ·₁= γ·₂=…= γ·_n)

Модель упруго-вязкого тела Максвелла:

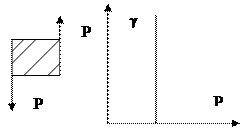
Жидкие и твердые тела – одинаковая сила сцепления.

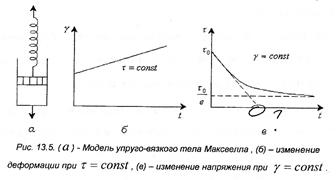
Максвеллом было дано представление, что

механические свойства тел являются

промежуточными между идеально жидкими и

идеально твердыми телами. Последовательное

соединение элементов Гука и Ньютона.

d γ/dτ = d γг/dτ = d γн/dτ

γ = Р/Е + Рτ/η – деформация. Скорость деформации: d γ/dτ = 1/Е ·d l/dτ + Р/η

1/Е · dP/ dτ + Р/η = 0 dP/P=E/η · dτ; Интегрируем получаем: ln (P/P₀)= – E/η · τ

P=P₀ · e — τ / λ – математическая модель Максвелла.,λ – время за которое напряжение в образце уменьшается в е раз. Характерна необратимая деформация тела.λ>>τ – релаксирует очень медленно (твердое тело), жидкое тело может вести себя как твердое.λ P_T – течение в системе

Р=Р_Т + η* · γ· – уравнение Бингама

P>P_T γ↑ (скорость деформации) γ·↑

Р = η · γ· → η = Р/ γ·= (Р_Т + η* · γ·)/ γ· = η* + Р_Т/ γ·

η – сопротивление течению всей системы; η*– течение и разрушение структуры

Содержание

Лако-красочные материалы — производство
Технологии и оборудование для изготовления красок, ЛКМ
Основные понятия и идеальные законы реологии
Реологические уравнения ньютоновской и неньютоновских вязких несжимаемых жидкостей
💡 Видео

Видео:Реология материалов. ВведениеСкачать

Лако-красочные материалы — производство

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Технологии и оборудование для изготовления красок, ЛКМ

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Основные понятия и идеальные законы реологии

Под структурой тел обычно понимают пространственное взаимное расположение составных ч-астей тела: атомов, молекул, мелких частиц. Структура разбавленных агрегативно устойчивых дисперсных систем по ряду свойств очень похожа на Структуру истинных растворов. Основное отличие состоит в том, что в дисперсных (гетерогенных) системах частицы дисперсной фазы и молекулы дисперсионной среды сильно различаются по размерам. Увеличение концентрации дисперсной фазы приводит к взаимодействию ее частиц, подобному ассоциации молекул и нонов в истинных растворах. Изменение свойств дисперсных систем с ростом концентрации происходит постепенно до тех пор, пока не наступит коагуляция частиц. В коллоидной химии понятия структуры и структурообразования принято связывать именно с коагуляцией. В процессе коагуляции происходит образование пространственной структурной сетки из частиц дисперсной фазы, что резко увеличивает прочность системы.

Таким образом, структурообразование в свободнодисперс — ных системах есть результат потери их агрегативной устойчивости. По мере увеличения прочности структуры свободнодис- персная система переходит в связиодисперсную систему. Появление и характер образующихся структур, как правило, определяют по механическим свойствам систем, к важнейшим из которых относятся вязкость, упругость, пластичность, прочность. Так как этн свойства непосредственно связаны со структурой тел, то их обычно называют структурно-механическими.

Структурно-механические свойства систем исследуют методами реологии — науки о деформациях и течении материальных систем. Реология изучает механические свойства систем по проявлению деформации под действием внешних — напряжений. В коллоидной химии методы реологии используют для исследования структуры и описания вязкотекучих свойств дисперсных систем.

Термин деформация означает относительное смещение точек системы, при котором не нарушается ее сплошность. Деформацию делят на упругую и остаточную. При упругой деформации структура тела полностью восстанавливается после снятия нагрузки (напряжения); остаточная деформация необратима, изменения в системе остаются и после снятия нагрузки. Остаточная деформация, при которой не происходит разрушения тела, называется пластической.

Среди упругих деформаций различают объемные (растяжение, сжатие), сдвиговые и деформации кручения. Они характеризуются количественно относительными (безразмерными) величинами. Например, при одномерном деформировании растяжение выражается через относительное удлинение:

Эта зависимость показана на рис. VII.4, б. Из нее следует, что к элементу сухого трения (идеально пластическому телу) не может быть приложено напряжение, превышающее Рг. Величина Рг отражает прочность структуры тела. При условии Р — Рт структура идеального пластического тела разрушается, после чего сопротивление напряжению полностью отсутствует.

Сравнение идеальных элементов (реологических моделей) показывает, что энергия, затраченная на деформацию упругого тела Гука, возвращается при разгрузке (после прекращения действия напряжения), а при деформа — Q ции вязкого и пластического тел энергия превращается в теплоту. В соответствии с этим тело Гука принадлежит

К КонсерватиВныМ системам, а другиЕ два^- к диссипативным (теряющим энер — г ню) ————— —————

Рис. VII.4. Модель идеально пластического тела Сеи-Венаиа — Кулона (а) н зависимость деформации этого тела от напряжения (б)

Видео:Лекция II-4. Математические модели твердого телаСкачать

Реологические уравнения ньютоновской и неньютоновских вязких несжимаемых жидкостей

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

РОССИЙСКОЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА

И.М. Астрахан

динамика вязких жидкостей

(ньютоновских и неньютоновских)

Допущено Учебно-методическим объединением вузов Российской Федерации по образованию в области горного дела в качестве учебного пособия для студентов вузов, обучающихся по специальности «Физические процессы горного или нефтегазового производства» направления подготовки дипломированных специалистов «Горное дело», по основной образовательной программе магистров «Физические процессы нефтегазового производства» направления подготовки бакалавров и магистров «Горное дело» и по направлению подготовки дипломированных специалистов «Нефтегазовое дело».

Москва 2005

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

РОССИЙСКОЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА

И.М. Астрахан

динамика вязких жидкостей

(ньютоновских и неньютоновских)

Москва 2005

Астрахан И.М. Динамика вязких жидкостей. Учебное пособие. – М.: РГУ нефти и газа им. И.М. Губкина, 2005 – 104 с.

В учебном пособии представлены разделы механики жидкости, которые не включены в курсы «Гидромеханика» и «Механика сплошных сред», но важны для подготовки дипломированных специалистов по специальности «Физические процессы нефтегазового производства» по направлению «Горное дело» и магистров по направлениям «Горное дело» и «Нефтегазовое дело». Представлены точные и приближенные решения уравнений движения ньютоновских и вязких неньютоновских жидкостей и методы получения этих решений. Рассматриваются проблемы неустойчивости ламинарных режимов течений и возникновение турбулентности в ньютоновских и неньютоновских вязких жидкостях.

Пособие предназначено для подготовки дипломированных специалистов по направлению 130400 «Горное дело» специальности 130401 «Физические процессы нефтегазового производства» и для подготовки магистров по направлениям 130400 «Горное дело» программа «Физические процессы нефтегазового производства» и 130500 «Нефтегазовое дело» программа «Гидромеханика нефтегазоконденсатных месторождений», а также может быть полезным для ряда других специальностей нефтегазового профиля.

Издание подготовлено на кафедре нефтегазовой и подземной гидромеханики РГУ нефти и газа им. И.М. Губкина.

проф. кафедры гидромеханики МГУ им. М.В. Ломоносова

нач. сектора ФГУП ЦИАМ им. П.И. Баранова

д.ф.-м. н., профессор Слободкина Ф.А.

Предисловие

Изучение вопросов механики жидкости занимает большое место в подготовке дипломированных специалистов и магистров по направлениям «Горное дело» и «Нефтегазовое дело». Данное учебное пособие написано на материале лекционного курса «Динамика вязких жидкостей», читаемого студентам пятого курса специальности «Физические процессы нефтегазового производства» РГУ нефти и газа им. И.М. Губкина.

Механика жидкости является одним из разделов механики сплошных сред – дисциплины, изучаемой студентами, обучающимися по направлениям «Горное дело» и «Нефтегазовое дело» на третьем курсе. В настоящем учебном пособии излагаются разделы механики жидкости не представленные в курсах «Гидромеханика» и «Механика сплошных сред», но важные для подготовки инженеров-исследователей и магистров.

Все вязкие жидкости можно разделить на ньютоновские, описываемые обобщенным законом Ньютона, дающим линейную связь между тензором напряжений и тензором скоростей деформаций и неньютоновские, которые не подчиняются этому закону. Неньютоновские жидкости образуют широкий класс разнообразных флюидов, весьма распространенных в нефтедобывающей и нефтехимической промышленности. Это ряд тяжелых нефтей, глинистые и цементные растворы, мазуты, растворы полимеров.

В первой главе приведена классификация неньютоновских жидкостей, представлены реологические уравнения неньютоновских вязких несжимаемых жидкостей и рассмотрены их свойства.

Во второй главе приведены уравнения движения сплошной среды в напряжениях и связь между напряжениями и характеристиками деформаций (реологические уравнения сред) для различных моделей вязких жидкостей.

В третьей главе даны точные решения уравнений движения ньютоновских и вязких неньютоновских жидкостей.

В четвертой и пятой главах рассмотрены приближенные решения, получаемые из уравнений движения путем отбрасывания в них членов, по своей величине малых в условиях рассматриваемых задач. Представлены два предельных случая. В первом случае силы трения значительно больше, чем силы инерции, во втором же они значительно меньше, чем силы инерции (течения в пограничном слое).

В пятой главе исследован пограничный слой в ньютоновских и вязкопластичных жидкостях. Для вязкопластичных сред рассмотрен ряд задач, решения которых позволяют упростить соотношения, используемые для определения реологических параметров вязкопластичных жидкостей по показаниям ротационных вязкозиметров различного типа.

В шестой главе рассмотрены неустойчивость ламинарных режимов течений и возникновение турбулентности в ньютоновских и вязкопластичных жидкостях. Приводятся результаты классических исследований для ньютоновских жидкостей и результаты, полученные автором для вязкопластичных жидкостей. Показано, что в вязкопластичных жидкостях возникновение неустойчивости основного ламинарного движения, которое затем может привести к образованию турбулентного движения, происходит двумя путями. Первый путь – появление неустойчивости после предельного разрушения структуры в ламинарном течении ньютоновской жидкости. Второй путь – когда неустойчивым становится основное ламинарное структурное течение вязкопластичной жидкости, то есть неустойчивость течения появляется до предельного разрушения структуры.

В учебном пособии наряду с классическим материалом изложены также результаты, полученные рядом исследователей и опубликованные лишь в научных журналах. Так, в четвертой главе (параграф 4) показано, что наложение пульсаций давления на течение степенных жидкостей в трубах в случае, когда силы инерции малы по сравнению с вязкими, приводит к увеличению расхода для псевдопластичных жидкостей и к его уменьшению для дилатантных.

Представленная в пособии библиография позволяет при необходимости уточнить детали излагаемых решений по первоисточникам.

Учебное пособие будет полезно для студентов, обучающихся по специальности 130401 «Физические процессы нефтегазового производства», ряда других специальностей нефтегазового профиля и для подготовки магистров по направлениям «Горное дело» и «Нефтегазовое дело».

Глава I

Реологические уравнения ньютоновской и неньютоновских вязких несжимаемых жидкостей