Рекуррентные уравнения и динамическое программирование

Правильными рекуррентными соотношениями ( уравнениями ) будем называть такие рекуррентные соотношения, у которых количество или значения аргументов у функций в правой части соотношения меньше количества или, соответственно, значений аргументов функции в левой части соотношения. Если аргументов несколько, то достаточно уменьшения одного из аргументов.

Особенно хочется обратить внимание на то, что соотношения должны быть определены для всех допустимых значений аргументов. Поэтому должны быть определены значения функций при начальных значениях параметров.

Просмотр содержимого документа
«РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ И ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ (теория)»

§1. Понятие задачи и подзадачи 1

§2. Сведение задачи к подзадачам 2

§3. Понятие рекуррентного соотношения 3

§4. Правильные рекуррентные соотношения 5

§5. Способ организации таблиц 6

5.1. Организация одномерных таблиц 7

5.2. Организация двумерных таблиц 8

§6. Способ вычисления элементов таблицы 9

6.1. Вычисление элементов одномерной таблицы 9

6.2. Вычисление элементов двумерной таблицы 10

6.3. Вычисление элементов двумерной таблицы с дополнительными ограничениями 12

§7. Программы на Паскале 14

Рекуррентные соотношения и динамическое программирование

1. Понятие задачи и подзадачи

При формулировке любой задачи необходимо определить исходные данные, которые мы будем называть параметрами задачи.

Например, если мы решаем задачу нахождения корней квадратного уравнения ax 2 + bx + c = 0, то эта задача определяется тремя параметрами – коэффициентами a, b и c.

Если же мы хотим решить задачу нахождения среднего арифметического некоторого набора чисел, то параметрами задачи будут количество чисел и их значения.

При этом нас пока не интересует конкретный алгоритм решения задачи. Мы хотим научиться решать задачу, сводя ее к решению подзадач. Здесь удобно думать об алгоритме как о некотором устройстве или некоторой функции, которые преобразуют входные параметры в некоторые выходные данные, являющиеся решением задачи.

Поэтому при описанном выше подходе любая задача может быть формализована в виде некоторой функции, аргументами которой могут являться такие величины, как:

Здесь и далее в качестве параметров будут рассматриваться целые неотрицательные числа.

Как правило, одним из аргументов задачи является количество параметров задачи. В том случае, когда по значению этого параметра можно определить конкретные значения других параметров, мы эти параметры будем опускать. Это обычно делается в случае, когда параметры заданы таблицей. Например, если нам необходимо найти сумму первых K элементов таблицы, то для решения задачи достаточно знать один параметр K, а все остальные параметры можно выбрать из таблицы.

После того, как задача формализована (представлена) в виде функции с некоторыми аргументами, определим понятие подзадачи . Здесь и далее в этой главе под подзадачей мы будем понимать ту же задачу, но с меньшим числом параметров или задачу с тем же числом параметров, но при этом хотя бы один из параметров имеет меньшее значение.

Пример 1. Найти самую тяжелую монету из 10 монет. Для формализации задачи определим функцию «Самая тяжелая монета», аргументами которой являются количество монет (10) и масса каждой из монет. Пока нас не интересует конкретный вид этой функции, для нас важнейшим фактором является факт, что она дает правильное решение.

Для данной задачи можно рассмотреть 9 подзадач, которые имеют меньшее число аргументов:

«Самая тяжелая монета» из 1 монеты,

«Самая тяжелая монета» из 2 первых монет,

«Самая тяжелая монета» из 3 первых монет,

«Самая тяжелая монета» из 9 первых монет.

Таким образом, у нашей функции «Самая тяжелая монета», аргументом является количество имеющихся монет, по которому можно определить конкретный вес каждой

монеты. Следовательно, рассмотренные подзадачи имеют меньшее количество аргументов, чем исходная задача.

Особо хочется отметить, что под подзадачей не следует понимать некоторые этапы решения задачи, такие, как организация ввода и вывода данных, их упорядочивание, или решение некоторой части поставленной задачи.

Одним из основных способов решения задач является их сведение к решению такого набора подзадач, чтобы, исходя из решений подзадач, было возможно получить решение исходной задачи.

При этом для решения исходной задачи может потребоваться решение одной или нескольких подзадач.

Пример 2. Задачу, сформулированную в примере 1, можно свести к различным наборам подзадач, например:

найти самую тяжелую из 9 монет, а затем найти самую тяжелую из 2 монет (найденной из 9 и оставшейся), или

найти самую тяжелую из 5 монет, затем самую тяжелую из других 5 монет, а затем самую тяжелую из 2 монет, найденных на преды­дущих шагах.

Возможны и другие наборы, но нетрудно заметить, что все они основываются на одной подзадаче: найти самую тяжелую из 2 монет.

В приведенном примере исходная задача сводится к подзадачам с меньшим числом параметров, в данном случае – с меньшим количеством монет.

Используя этот же принцип можно решить задачу нахождения НОД двух чисел.

Пример 3. Найти наибольший общий делитель (НОД) двух натуральных чисел N и M.

Если числа равны, то их НОД равен одному из чисел, т. е. НОД(N, M) = N.

Рассмотрим случай, когда числа не равны. Известно, что

Последние соотношения и обеспечивают основной принцип сведения решения задачи к подзадачам: значение одного из параметров стало меньше, хотя их количество и осталось прежним.

Таким образом, решение задачи нахождения НОД(N, M) при различных значениях N и M сводится к двум подзадачам:

Найденный способ сведения решения исходной задачи к решению некоторых подзадач может быть записан в виде соотношений, в которых значение функции, соответствующей исходной задаче, выражается через значения функций, соответствующих подзадачам. При этом важнейшим условием сведения является тот факт, что значения аргументов у любой из функций в правой части соотношения меньше значения аргументов функции в левой части соотношения. Если аргументов несколько, то достаточно уменьшения одного из них.

Особенно хочется обратить внимание на то, что соотношения должны быть определены для всех допустимых значений аргументов.

Пример 4. Рассмотрим задачу нахождения суммы N элементов таблицы A.

Пусть функция S(N) соответствует решению нашей исходной задачи. Эта функция имеет один аргумент N – количество суммируемых элементов таблицы A. Понятно, что для поиска суммы N элементов достаточно знать сумму первых N – 1 элементов и значение N-го элемента. Поэтому решение исходной задачи можно записать в виде соотношения

Следует отметить, что это соотношение справедливо для любого количества элементов N 1. Это соотношение можно переписать в виде

Однако пока это соотношение не определено при N = 1. К приведенному выше соотношению необходимо добавить соотношение S(1) = a₁.

Заметим, что на практике применяются имеющие тот же смысл соотношения

Последовательное применение первого соотношения при i = 1, 2, . N и используется при вычислении суммы N элементов.

нц для i от 1 до N (4. 1)

Здесь и далее в круглых скобках будут записываться аргументы функции, а в квадратных – индексы элементов массива. При этом имя функции и имя массива, в котором хранится значение этой функции, могут совпадать.

Индекс у S может быть опущен, но смысл соотношения при этом остается прежним. Это связано с тем, что для вычисления следующего элемента таблицы S необходимо знать только предыдущий.

Пример 5 . Вычислить сумму S = 1 + 1/x + 1/x 2 + . + 1/x N при x, не равном 0.

Как и в предыдущем примере можно записать следующее соотношение:

Конечно, можно и эти соотношения использовать для написания программы. При этом у нас возникла новая задача – найти способ вычисления a(i). Для этого можно воспользоваться тем же приемом – попытаться вычислить a(i) через значение a(i – 1). Соотношение между значениями a(i) и a(i – 1) имеет следующий вид:

Поэтому поставленную задачу можно решить следующим образом.

нц для i от 1 до N (4. 2)

Отметим, что и в этом случае индексы при S и a можно опустить в связи с тем, что для вычисления текущего элемента каждой из таблиц достаточно знать только значение предыдущего элемента.

Соотношения, связывающие одни и те же функции, но с различными аргументами, называются рекуррентными соотношениями или рекуррентными уравнениями.

Правильными рекуррентными соотношениями ( уравнениями ) будем называть такие рекуррентные соотношения, у которых количество или значения аргументов у функций в правой части соотношения меньше количества или, соответственно, значений аргументов функции в левой части соотношения. Если аргументов несколько, то достаточно уменьшения одного из аргументов.

Особенно хочется обратить внимание на то, что соотношения должны быть определены для всех допустимых значений аргументов. Поэтому должны быть определены значения функций при начальных значениях параметров.

В приведенных примерах соотношения связывали функции только с двумя различными параметрами: S(i) и S(i – 1), а также a(i) и a(i – 1) для любого натурального i. При этом были определены начальные значения S(0) и a(0).

Отметим, что без этих начальных значений рекуррентное соотношение

было бы неправильным, так как оно не определено при i = 1.

Конечно, могут быть и более сложные соотношения, связывающие более двух функций.

Пример 6 . Одной из наиболее известных числовых последовательностей являются числа Фибоначчи, которые определяются следующим рекуррентным соотношением

В этом случае для вычисления значения F(N), которое хранится в F[N], можно воспользоваться следующим алгоритмов.

нц для i от 2 до N (4. 3)

 F[i]: = F[i – 1] + F[i – 2]

При этом в приведенном фрагменте уже нельзя просто опустить индексы, хотя в принципе можно вычислить значение F(N) без использования таблицы, но это уже вопрос способа реализации алгоритма.

Пример такой реализации приводится ниже.

нц для i от 2 до N (4. 4)

В приведенной реализации используется тот факт, что для вычисления текущего элемента таблицы нам достаточно знать только значения двух предыдущих.

Из рассмотренных примеров видно, что важнейшим моментом при решении задачи является способ сведения задачи к подзадачам. Но не менее важным вопросом является и способ построения решения исходной задачи из решений подзадач. Одним из наиболее эффективных способов построения решения исходной задачи является использование таблиц для запоминания решений подзадач. Такой метод решения задач называется методом динамического программирования.

Как уже говорилось раньше, подзадача может быть формализована в виде функции, которая зависит от одного или нескольких аргументов. Если мы возьмем таблицу, у которой количество элементов равно количеству всех возможных различных наборов аргументов функции, то каждому набору аргументов может быть поставлен в соответствие элемент таблицы. Вычислив элементы таблицы (решения подзадач), можно найти и решение исходной задачи.

Одним из способов организации таблиц является такой подход, когда размерность таблицы определяется количеством аргументов у функции, соответствующей подзадаче.

Пример 7 . Рассмотрим задачу нахождения произведения 10 элементов таблицы A.

Пусть функция P(10) соответствует решению нашей исходной задачи. В данном случае у функции только один параметр – количество элементов. Для поиска произведения 10 элементов достаточно знать произведение первых 9 элементов и значение 10-го элемента. Поэтому решение исходной задачи можно записать в виде соотношения

Следовательно, это соотношение может быть определено

для любого i, 2  i  10:

На практике для рассматриваемой задачи чаще используется рекуррентное соотношение, имеющее тот же смысл, но с другим начальным значением:

нц для i от 1 до N (4. 5)

Так как у нашей функции один аргумент – количество сомножителей, то для решения задачи достаточно использовать одномерную таблицу. При этом количество элементов таблицы определяется количеством различных значений аргумента. В приведенном примере размерность массива равна 10. Если бы мы решали задачу поиска произведения 20 элементов, то для реализации рекуррентного соотношения нам было бы достаточно одномерной таблицы с 20 элементами.

Таким образом, размерность таблицы, достаточная для реализации рекуррентных соотношений, определяется количеством аргументов у функций, соответствующих подзадачам. Количество же элементов по каждой размерности (количество элементов в строках, столбцах) определяется количеством возможных значений соответствующего аргумента.

Еще раз обратим внимание, что нас пока не очень интересуют вопросы реализации алгоритма, при которой минимизируется такая характеристика, как размер используемой оперативной памяти. Будем считать, что памяти компьютера достаточно для хранения соответствующей таблицы.

Пример 8. Для данной прямоугольной таблицы A размера 5×6 построить прямоугольную таблицу B того же размера, элементы которой обладают следующим свойством: элемент B[i, j] равен максимальному из элементов таблицы B, которые расположены левее и выше позиции (i, j), включая также позицию (i, j). При этом считается, что позиция (1, 1) – верхняя левая позиция прямоугольной таблицы (при i = 3 и j = 4 интересующая нас часть показана на Рис. 1).

Пусть T(i, j), обозначает функцию, вычисляющую элемент B[i, j].

Определим сначала значения элементов таблицы B, расположенных в первой строке и в первом столбце. Получим:

Эти соотношения следуют из того факта, что в этих случаях интересуемая нас область матрицы A ограничена только элементами первой строки или первого столбца матрицы.

При 2  i  5 и 2  j  6 для этой функции можно записать следующее рекуррентное соотношение:

Действительно, величина T(i – 1, j) соответствует максимальной величине элементов таблицы A в той ее части, которая определяется значением индексов i – 1 и j, а величина T(i, j – 1) – максимальной величине элементов таблицы A, определяемой индексами i и j – 1. Поэтому эти величины учитывают значение всех элементов матрицы A в той ее части, которая определяется значением индексов i и j за исключением одного элемента A[i, j].

Для реализации этих рекуррентных соотношений достаточно двумерной (прямоугольной) таблицы, так как у функции T два аргумента. Важно отметить, что при этом мы можем отождествить величины T(i, j) и B[i, j]. Тогда фрагмент алгоритма можно записать следующим образом:

нц для j от 2 до 6

 В[1, j] = max(В[1, j – 1], A[1, j])

нц для i от 2 до 5 (4. 6)

 В[i, 1] = max(В[i – 1, 1], A[i, 1])

нц для i от 2 до 5

 нц для j от 2 до 6

  B[i, j] = max(B[i, j – 1], B[i – 1, j])

  B[i, j] = max(B[i, j], A[i, j])

После того, как найдено сведение задачи к подзадачам и определены рекуррентные соотношения, соответствующие этому сведению, необходимо определить наиболее рациональный способ вычисления элементов таблицы.

Для одномерной таблицы таким способом обычно является последовательное вычисление элементов, начиная с первого.

Пример 9. Определить, сколькими различными способами можно подняться на 10-ю ступеньку лестницы, если за один шаг можно подниматься на следующую ступеньку или через одну.

Пусть K(10) – задача поиска количества способов подъема на 10 ступеньку. Определим i-ю подзадачу нашей задачи как задачу поиска количества способов подъема на i-ю ступеньку.

Исходя из условия задачи, на 10 ступеньку можно подняться непосредственно с 8-й и 9-й ступенек. Поэтому, если мы знаем количество способов подъема K(8) и K(9) на 8 и 9 ступеньки, то количество способов подъема на 10 ступеньку может быть определено как K(10) = K(8) + K(9).

Такое соотношение получается потому, что любой способ подъема на 8-ю ступеньку превращается в способ подъема на 10-ю ступеньку добавлением перешагивания через 9-ю ступеньку, а любой способ подъема на 9-ю ступеньку превращается в способ подъема на 10-ю ступеньку добавлением подъема с 9 на 10-ю ступеньку. Все эти способы различны. Аналогичное соотношение справедливо для любой ступеньки i, начиная с третьей, K(i) = K(i – 2) + K(i – 1).

Осталось определить значения K(1) и K(2), которые равны: K(1) = 1, K(2) = 2.

Следовательно, для решения задачи достаточно одномерной таблицы с 10 – ю элементами, для которой необходимо последовательно вычислить значения элементов таблицы согласно приведенным выше рекуррентным соотношениям.

нц для i от 2 до 10 (4. 7)

 K[i]: = K[i – 1] + K[i – 2]

Полученные рекуррентные соотношения не отличаются от рекуррентных соотношений примера 6, поэтому могут быть реализованы без использования таблицы.

Пример 10 . В таблице c N строками и M столбцами, состоящей из 0 и 1, необходимо найти квадратный блок максимального размера, состоящий из одних единиц. Под блоком понимается множество элементов соседних (подряд идущих) строк и столбцов таблицы. Интересующая нас часть показана на рис. 2.

Положение любого квадратного блока может быть определено его размером и положением одного из его углов.

Пусть T(i, j) есть функция, значение которой соответствует размеру максимального квадратного блока, состоящего из одних единиц, правый нижний угол которого расположен в позиции (i, j). Функция T(i, j) вычисляет элемент таблицы B[i, j]. Для примера на рис. 2 значения T(i, j) будут иметь вид

Таким образом, наша задача свелась к вычислению максимального значения функции Т при всевозможных значениях параметров i и j. Этой функции может быть поставлена в соответствие таблица размера N*M.

Определим сначала значения элементов таблицы В, расположенных в первой строке и в первом столбце. Получим:

Эти соотношения следуют из того факта, что в этих случаях рассматриваемая область матрицы А содержит только один элемент матрицы.

При 2  i  N и 2  j  M для этой функции можно записать следующие рекуррентные соотношения:

Первое соотношение показывает, что размер максимального единичного блока с правым нижним углом в позиции (i, j) равен нулю в случае A[i, j] = 0.

Убедимся в правильности второго соотношения. Действительно, величина B[i – 1, j] соответствует максимальному размеру единичного блока таблицы A с правым нижним углом в позиции (i – 1, j). Тогда размер единичного блока с правым нижним углом в позиции (i, j) не превышает величину B[i – 1, j] + 1, так как к блоку в позиции (i – 1, j) могла добавиться только одна строка. Величина B[i, j – 1] соответствует максимальному размеру единичного блока таблицы A с правым нижним углом в позиции (i, j – 1). Тогда размер единичного блока с правым нижним углом в позиции (i, j) не превышает величину B[i, j – 1] + 1, так как к блоку в позиции (i – 1, j) мог добавиться только один

столбец. Величина B[i – 1, j – 1] соответствует максимальному размеру единичного блока таблицы A с правым нижним углом в позиции (i – 1, j – 1). Тогда размер единичного блока с правым нижним углом в позиции (i, j) не превышает величину B[i – 1, j – 1] + 1, так как к блоку в позиции (i – 1, j – 1) могли добавиться только одна строка и один столбец. Итак, размер единичного блока с правым нижним углом в позиции (i, j) равен min<B[i – 1, j], B[i, j – 1], B[i – 1, j – 1]> + 1.

нц для j от 2 до 6

нц для i от 2 до 5

нц для i от 2 до 5

 нц для j от 2 до 6

   B[i, j]: = min(B[i, j – 1], B[i – 1, j])

   B[i, j]: = min(B[i, j], B[i – 1, j – 1]) + 1

1. Вычисление элементов двумерной таблицы с дополнительными ограничениями

Пример 11 . На складе имеется 5 неделимых предметов. Для каждого предмета известна его стоимость (в рублях) и масса (в кг). Величины стоимости и массы являются натуральными числами. Ваша цель состоит в том, чтобы определить максимальную суммарную стоимость предметов, которые вы можете унести со склада при условии, что суммарная масса предметов не должна превышать 16 кг.

Пусть элемент C_i таблицы C соответствует стоимости i-го предмета, а элемент M_i таблицы M – массе i-го предмета. Будем считать, что предметы пронумерованы в порядке их следования в таблицах.

Пусть T обозначает функцию, значение которой соответствует решению нашей задачи. Аргументами у этой функции является количество предметов (по этому аргументу можно определить их стоимости и массы соответствующих предметов), а также максимальная суммарная масса, которую можно унести.

Для нашей задачи T(5, 16) определим подзадачи T(i, j), где i обозначает количество начальных предметов, из которых можно осуществлять выбор, а j определяет максимально возможную суммарную массу уносимых предметов. Отметим, что определенный таким образом первый параметр i определяет как количество предметов для подзадачи, так и значения их стоимостей и масс, определяемых из таблиц C и M.

Определим сначала начальные значения функции T. При нулевых значениях одного из аргументов значение функции равно нулю:

Определим возможные значения функции T(i, j) при ненулевых значениях аргументов.

Решение подзадачи, соответствующей функции T(i, j) может быть сведено к двум возможностям: уносится ли при наилучшем решении предмет с номером i или нет.

Если предмет не уносится, то решение задачи с i предметами сводится к решению подзадачи с i – 1 предметами, т. е.

Если предмет c номером i уносится, то это уменьшает максимально возможную суммарную массу для i – 1 первых предметов на величину M[i], одновременно при этом увеличивая значение решения для оставшихся предметов T(i – 1, j – M[i]) на величину C[i], т. е.

При этом необходимо учитывать, что вторая ситуация возможна только тогда, когда масса i-го предмета не больше значения j.

Теперь для получения наилучшего решения нам необходимо выбрать лучшую из этих двух возможностей. Поэтому рекуррентное соотношение при i  1 и j  1 имеет вид

Пусть заданы следующие значения стоимости и массы для 5 предметов:

Таблица значений функции T, которую мы также назовем T, выглядит следующим образом:

Видео:Зачем рекурсия и динамическое программированиеСкачать

Рекуррентные уравнения и динамическое программирование

Решение задачи 1.

Можно, конечно, каждый раз вычислять очередное p!, затем 1/p!, и полученное слагаемое добавлять к сумме. Но обратим внимание на следующее очевидное равенство:

и программа вычисления запишется следующим образом

Решение задачи 2.

1) Самое простое — это перебрать все возможные комбинации шести цифр и подсчитать число «счастливых» билетов.

Условие if во вложенных циклах будет проверяться 10 6 раз, поэтому будем говорить, что сложность этого алгоритма 10 6 .

2) Обратим внимание на то, что в «счастливом» билете последняя цифра a6 однозначно определяется первыми пятью:

3) Если комбинаций a1 a2 a3 первых трех цифр с суммой T=a1+a2+a3 насчитывается C[T], то всего «счастливых» билетов с суммой половины T=a1+a2+a3=a4+a5+a6 будет C[T]*C[T]. Всех возможных сумм T-28 (от 0=0+0+0 до 27=9+9+9). Подсчитаем C[i], i=0, . 28, затем найдем интересующее нас количество «счастливых» билетов

C[0] 2 + C[1] 2 + . + C[27] 2 .

Заметим, что «счастливых» билетов с суммой T столько же, сколько и с суммой 27-T. Действительно, если билет a1 a2 a3 a4 a5 a6 с суммой T — «счастливый», то таковым же является и билет (999999 — a1 a2 a3 a4 a5 a6) с суммой 27-T. Поэтому число билетов можно вычислять и по формуле

т.е.рассматривать только суммы T от 0 до 13.

Сложность этого алгоритма 10 3 .

4) В пункте 3 мы перебирали комбинации цифр и искали количество комбинаций с суммами C[T]. Сейчас мы пойдем от суммы T, и по ней будем определять, какое количество комбинаций a1 a2 a3 ее имеет.

Минимальное значение, которое может принимать a1, — это MAX. Член T-18 появляется из следующих соображений: пусть a2=a3=9, тогда a1=T-18, но a1 не может быть меньше 0. Максимальное значение a1=MIN (так как a2 и a3 неотрицательны, то a1

Решение задачи 3.

Задача имеет очевидное решение, которое состоит в генерации всех 2*n-разрядных чисел и проверке их на требуемое свойство. Однако общее количество таких чисел равно 10 2n и поэтому при n>3 практически очень трудно получить результат на ЭВМ. Следовательно необходимо разработать алгоритм, не требующий генерации чисел.

Определим через S(k,i) количество k-разрядных чисел, сумма цифр которых равна i. Например, S(2,3)=4, так как существует 4 двуразрядных числа (03,12,21,30), сумма цифр которых равна 3. Легко заметить, что S(1,i)=1 при i 9. Предположим теперь, что мы сумели вычислить значения величин S(n,i) для всех i от 0 до 9*n, т.е. мы знаем, сколько существует n-разрядных чисел с суммой цифр, равной 0,1. 9*n (максимальное число цифр в n-разрядном числе). Тогда нетрудно убедиться, что общее количество ‘счастливых’ 2*n-разрядных чисел равно

Действительно, каждое ‘счастливое’ 2*n-разрядное число может быть получено склейкой двух произвольных n-разрядных чисел с одинаковой суммой цифр.

Таким образом, необходимо уметь вычислять значения величин S(k,i) для всех k 1 )+S(k,i-ц 2 )+.

где ц 1 ,ц 2 . — возможные добавленные цифры. Ясно, что это 0,1. m где m=min(9,i). Следовательно,

Решение задачи 4.

Очевидное решение задачи предполагает разложение числа N на всевозможные суммы таким образом, чтобы каждое слагаемое в сумме не превосходило k. Очевидно, что таких разложений очень много, особенно если учитывать, порядок слагаемых в разложении существенен, так как он соответствует различной последовательности ходов фишки.

Обозначим через S(i) количество различных путей, по которым фишка может пройти поле от начала до позиции с номером i. Предположим теперь, что для любого j от 1 до i известны значения величин S(j). Задача состоит в определении правила вычисления значения S(i+1), используя значения известных величин. Легко заметить, что в позицию с номером i+1 фишка может попасть из позиций i, i-1. i-k. Следовательно,

Таким образом, вычисляя последовательно значения величин S(1), S(2). S(N) по описанному выше правилу, получаем значение S(N), которое и указывает общее количество различных путей, по которым фишка может пройти поле от начала до позиции с номером N.

Решение задачи 5.

Если покупатель отдаст все свои купюры продавцу, то понятно, что для решения исходной задачи размер минимальной сдачи, которую продавец не может вернуть, используя любые имеющиеся теперь у него купюры C[i] (его и покупателя). Для этого удобно отсортировать купюры согласно их достоинства в порядке неубывания.

Предположим, что продавец может вернуть любую сдачу от 1 до S, используя только меньшие i купюр. Для следующей (i+1)-ой купюры достоинства C[i+1] возможны 2 ситуации.

1. C[i+1] S+1. Тогда понятно, что продавец не может вернуть сдачу S+1.

Опишем процедуру вычисления S.

Если значение S не меньше суммарного количества денег покупателя, то покупатель может купить товар любой доступной ему стоимости, точно рассчитавшись за покупку. Иначе P=A[1]+. +A[N]-S.

Решение задачи 6.

Решается аналогично задаче 5.

Решение задачи 7.

Если S>H(1)+. +H(n), то сумму выплатить нельзя.

Если покупатель отдаст все свои купюры продавцу, то понятно, что для решения исходной задачи надо определить, может ли продавец вернуть сумму H(1)+. +H(n)+B(1)+. +B(l)-S, используя любые имеющиеся теперь у него купюры M[i] (его и покупателя). Для этого удобно отсортировать купюры согласно их достоинства в порядке неубывания.

Решим чуть более общую задачу: найдем все непредставимые данными купюрами суммы на промежутке от 0 до P.

Заведем массив A[0 .. P] натуральных чисел. Элемент A[i]=1, если мы можем выплатить сумму i (т.е. существует набор купюр суммарного достоинства i), и A[i]=0 иначе.

Будем строить всевозможные суммы, используя последовательно 0,1,2. N купюр.

Очевидно, что сумма из ноля купюр — это ноль, поэтому сначала A[0]=1.

Предположим, что мы нашли всевозможные суммы, которые можно составить, используя не более (k-1) — ой купюры M[1], . M[K-1]. Добавим еще одну купюру M[k].

Теперь мы можем выплатить следующие суммы:

1) Все суммы, которые можно было составить с помощью купюр M[1], . , M[K-1].

2) Все суммы, которые можно было составить с помощью купюр M[1], . , M[K-1], увеличенные на M[K].

Расстановка новых пометок в массиве A может выглядеть следующим образом:

for i:=P-M[K] downto 0 do

Мы проходим по массиву справа налево для того, чтобы не использовать повторно впервые образованную на данном шаге сумму.

После выполнения n+l шагов алгоритм заканчивает работу.

Если известно, что H(1)+. +H(n)+B(1)+. +B(l)-S не превосходит некоторой константы D, то тогда массив A имеет смысл брать не из P, а из D элементов.

Решение задачи 8.

Решается аналогично задаче 7. При этом достаточно завести массивы

var A, KOL, PredSum, B: array [0..P] of byte;

Назначение массива A — как и в предыдущей задаче. Массив В служит для временного хранения предыдущих сумм. Элементы KOL[i] и PredSum[i] указывают соответственно минимальное количество элементов, участвующих в получении суммы со значением i и предыдущую сумму, из которой была получена добавлением одного слагаемого сумма i. Формирование этих массивов осуществляется параллельно с заполнением массива А. Сначала

Почему мы не можем непосредственно записывать новую информацию о предыдущей сумме в массив PredSum? Обратите внимание, что массивы A и KOL дублируют друг друга. Напишите тот же фрагмент программы, объединив функции массивов A и KOL в одном массиве A. После завершения работы предыдущего фрагмента если A[S]=1, то сумму S набрать можно с помощью KOL[S] купюр. Предыдущая сумма (до добавления последней купюры) была S’= PredSum[S], следовательно последняя купюра есть S-PredSum[S]. Аналогично выписываем купюры, требуемые для представления суммы S’ (используя PredSum[S’]).

Решение задачи 9.

Очевидное решение задачи состоит в использовании некоторой процедуры, которая по заданным координатам (номеру строки i и номеру столбца j) элемента определяет максимальное значение элементов, расположенных в нужной части матрицы A.

Однако нетрудно заметить, что для элементов первого столбца матрицы В справедливо соотношение B[i,1]=A[i,1], i=1. N. Вычисление же других столбцов можно проводить следующим образом:

При этом необходимо учитывать, что индексы элементов должны находится в пределах границ массива.

Решение задачи 10.

В элемент a[i,j] матрицы будем заносить длину максимальной стороны квадрата из единиц, у которого элемент (i,j) есть верхний левый угол (очевидно, что если a[i,j]=0, то квадрат построить нельзя).

Матрицу A будем просматривать по строкам справа налево, снизу вверх.

Предположим, что текущий просматриваемый элемент a[i,j] (все элементы, лежащие в строках с номерами больше i, равно как и все элементы строки i правее a[i,j] считаются уже к этому моменту просмотренными).

Если элемент a[i,j]=0, то его значение остается нулевым. Если же a[i,j]=1, то для того, чтобы найти максимальный размер квадрата из единиц, у которого (i,j) — верхний левый угол, проанализируем уже просмотренные элементы a[i,j+1], a[i+1,j+1], a[i+1,j] — соответственно длины сторон максимальных квадратов с левым углом справа, по диагонали вниз и просто вниз от данного элемента. Квадрат с верхним левым углом (i,j) может протянуться вправо на больше чем на a[i+1,j]+1, вниз — не больше чем на a[i,j+1]+1 и по диагонали не больше чем на a[i+1,j+1]+1. Следовательно, максимальная сторона квадрата есть

Решение задачи 11.

Пусть верхний левый угол матрицы имеет индекс (1,1).

Будем для каждой строки i формировать вектор p[1..M] такой, что p[j] есть число последовательных единичных элементов в столбце j, начиная с элемента (i,j) и выше его. Таким образом, если p[j]=0, то A[i,j]=0, а если p[j]=u>0, то

а элемент A[i,j-u] нулевой (если, конечно, такой элемент есть в матрице, т.е. если j-u>0).

Тогда площадь (сумма элементов) единичного прямоугольника S_i(L,R) с нижними правым и левым углами в элементах (i,R) и (i,L) соответственно есть площадь основания (R-L+1) умноженная на высоту этого прямоугольника

h(L,R)=минимальное p[i] по всем j, изменяющимся от L до R.

Для каждой строки i надо найти максимум величины S_i(L,R) при 1

Решение задачи 12.

Комбинируем идеи пунктов a) и c) задачи 16 (глава «Сортировки и последовательности»). Пусть элемент C[i,j] массива C есть следующая сумма

Переменная MaxSoFar имеет то же самое назначение, что и раньше,MaxFndingHere есть максимальное значение суммы элементов прямоугольной подматрицы с правым нижним углом (i,j) и высоты k.

Решение задачи 13.

Для решения пункта 1 задачи достаточно воспользоваться

тем фактом, что для определения минимальной величины штрафа, взимаемого за проход в клетку i-той строки достаточно знать минимальные величины штрафа, взимаемого за проход в клетки (i-1)-той строки, которые являются соседними рассматриваемой клетке. Поэтому алгоритм решения пункта 1 следующий:

Для решения пункта 2 можно воспользоваться алгоритмом Дейкстры нахождения минимального пути в графе из главы ‘Графы’.

Решение задачи 14.

а) Обозначим вершины N-угольника x(0), . x(N-1) в порядке обхода по контуру. В дальнейшем будем считать, что если у нас в выкладках встречается вершина с индексом k, то это то же, что и вершина с номером k mod N (остаток от деления k на N).

Рассмотрим выпуклый L-угольник, вершинами которого являются L

последовательных вершин данного N-угольника, начиная с x(p) и до x(p+L-1) (в порядке обхода по контуру). У этого L-угольника будем считать, что отрезок (x(p),x(p+L-1)) — это его диагональ. Сумму диагоналей этой фигуры обозначим S(p,p+L-1).

Очевидно, что по условию задачи:

S(p,p)=0; S(p,p+1)=0 (у точки и отрезка нет диагоналей),

(тут d(p,p+2) — длина отрезка (x(p),x(p+2))).

Предположим, что мы знаем S(p,p+L-1) для всех p=0, . N-1 и L=1. k.

Мы знаем, что диагонали разбивают k+1 угольник на треугольники, и что (x(p),x(p+k)) — диагональ, т.е. одна из сторон какого-то треугольника. Итак, мы зафиксировали две вершины треугольника x(p) и x(p+k). Третьей вершиной может быть либо x(p+1), либо x(p+2). либо x(p+k-1). Если мы считаем, что третья вершина это x(i), то сумма диагоналей будет

Тут мы уже знаем S(p,i) и S(i,k) — они, по предположению, были вычислены на предыдущих шагах. d(p,p+k) — это расстояние между вершинами x(p) и x(p+k), его мы тоже можем вычислить.

Так как нас интересует минимальная сумма триангуляции (разбиения на треугольники), то мы ищем выражение (1) с минимальным значением

Находим S(p,p+k) для каждого p=0. N-1.

Минимум S(p,p+N-2) по p=0. N-1, и даст искомую триангуляцию (действительно, S(p,p+N-2) есть стоимость разбивки фигуры после проведения N-3 диагоналей).

б) Алгоритм остается тем же, за исключением того, что вместо формулы (2) надо использовать следующую:

S(p,p+k)=,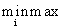

где S(p,p+k) — длина максимальной диагонали в фигуре с вершинами x(p), x(p+1), . x(p+k) (отрезок (x(p),x(p+k)) считается диагональю). Мы берем минимум по всем возможным разбивкам фигуры, а стоимость разбивки определяется как максимум из длины диагонали d(p,p+k) и длин максимальных диагоналей S(p,i) и S(i,k).

Решение задачи 15.

Будем считать, что вектор С определяет веса элементов, а вектор В — стоимость.

Обозначим через F[k,y] величину наибольшей суммарной стоимости элементов с номерами не большими k, суммарный вес которых не превышает y. Покажем, как можно вычислить значение F[k+1,y], используя величины с меньшими значениями индексов.

Понятно, что величина F[k+1,y] может соответствовать множеству элементов, которое содержит или не содержит элемент k+1. Если множество не содержит элемент k+1, то F[k+1,y]=F[k,y]. Иначе F[k+1,y]=B[k+1]+F[k,y-С[k+1]], т.е. максимальная суммарная стоимость есть стоимость k+1 элемента плюс максимальная стоимость элементов с номерами не большими k, суммарный вес которых не превышает величины y-С[k+1].

Таким образом, мы имеем рекуррентную формулу вычисления величин

Вычисляя последовательно элементы матрицы F, учитывая при этом, что F[0,y]=0 для любого y, и F[j,0] для любого j, получим значение F[N,A], которая является значением максимально возможной стоимости.

Для выяснения номеров элементов, вошедших в множество, достаточно, начав с элемента с индексами [i,y] (которые вначале равны N и A соответственно),сравнить его со значением F[i-1,y]. Если значения равны, то i элемент не входит в множество, а процесс повторяется для элемента с индексами [i-1,y]. В случае неравенства элементов элемент i входит в множество, а процесс повторяется для элемента с индексами [i-1,y-C[i]]. Процесс выполняется для всех i от N до1.

Решение задачи 16.

Для x=a(1). a(m) и y=b(1). b(n), a(i) и b(i) символы, 1 ij >

где P ij =1 если a(i)b(i) и P ij =0 иначе (в правой части приведенного выше выражения первому элементу в min соответствует операция удаления из строки a(1). a(i-1)a(i) последнего элемента a(i), после чего за d[i-1,j] операцию строка a(1). a(i-1) преобразуется в строку b(1). b(j), второму элементу — операция вставки символа b(j) в конец строки b(1). b(j-1), полученной за d[i,j-1] операцию из строки a(1). a(i), а третьему — контекстная замена a i на b j , замена осуществляется в случае a i b j (тогда P ij =1) и не происходит при совпадении a i и b j ).

Получаем необходимое d(x,y)=d[m,n].

Алгоритм может быть записан так:

Решение задачи 17.

Делается аналогично задаче 16.

Решение задачи 18.

Пусть строка S 1 состоит из цифр 0 и 1 и имеет длину N, а строка S 2 (из символов A и B) — длину M.

Заведем матрицу А размера N на M, при этом строки матрицы помечаются i-ой цифрой строки S 1 , а j-й столбец — j-м символом строки S 2 .

Возьмем в качестве примера S 1 =’00110′, S 2 =’AAAABBAA’.

Первая цифра строки S 1 (цифра 0) может быть преобразована в одну из последовательностей букв ‘A’,’AA’,’AAA’,’AAAA’, являющиеся префиксами строки S 2 . Заносим символ ‘x’ в те столбцы первой строки, буквы-пометки которых соответствуют последним буквам возможных последовательностей. Таким образом, помечаются элементы A[1,1], A[1,2], A[1,3] и A[1,4].

Шаг алгоритма: будем преобразовывать очередную цифру S 1 [i], которой соответствует строка i.

Находим ‘x’ в предыдущей строке при просмотре ее слева направо (этому столбцу соответствует последняя буква в какой-то из непустых последовательностей букв, порожденных на предыдущем шаге). Если текущую цифру можно преобразовать в последовательность букв, помечающих следующие за данным столбцы, то в этих столбцах в данной строке ставим ‘x’.

Далее от места над последней помеченной ячейкой ищем в предыдущей строке ‘x’ и, когда находим, повторяем указанные выше операции.

Эти действия проводим далее для i=2. N.

Вид матрицы после N шагов:

Замечание: Можно обойтись и одномерным массивом. В самом деле, при заполнении следующей строки мы обращаемся только к элементам предыдущей строки, к каждому — по одному разу.

Алгоритм (без учета замечания) может быть следующим:

Напишите программу, использующую одномерный массив.

Решение задачи 19.

Определим через F[i,j] минимальное число операций, которое требуется для перемножения группы матриц с номерами от i до j включительно. Ясно, что F[i,i]=0. Перемножение матриц в такой группе может производиться различными способами, а именно, производить сначала перемножение наилучшим способом группы от i до k, затем от k+1 до j, наконец перемножить получившиеся матрицы. Понятно, что k может быть величиной от i до j-1. Учитывая требование получить наилучший результат, величина F[i,j] определяется как

где k может быть величиной от i до j-1, n[i], n[k+1], m[j] определяют размеры матриц, получившихся при перемножении в группах.

Решение задачи 20.

а). Пусть К(L,i) обозначает множество возрастающих подпоследовательностей длины L, которые составлены из элементов с номерами от 1 до i-1. Понятно, что их может быть очень много. Однако их число можно существенно сократить, воспользовавшись следующим фактом: из двух цепочек длины L более перспективной будет цепочка, у которой величина последнегоэлемента меньше, так как ее может продолжить большее числоэлементов. Пусть S(L,i) — это именно такая самая перспективная цепочка длины Lс минимальным по величине последним элементом, а S(i) – это множество всех цепочек S(L,i) со всевозможными L. Понятно, что в S(i) содержится не более i-1 цепочек (с длинами 1. i-1). Пусть мы знаем S(i).

Для того, чтобы определить, какие цепочки может продолжать i-й элемент,достаточно знать последние элементы перспективных цепочек.

Для этого удобно завести массив адресов АДР последних элементов перспективных цепочек длины 1,2. n. При этом легко понять, что последний элемент перспективной цепочки длины s не превышает последнего элемента перспективной цепочки длины s+1. Следовательно, для очередного i-го элемента достаточно найти только максимальную длину перспективной цепочки, для которой он будет последним. Понятно, что это будет цепочка максимальной длины, последний элемент которой меньше текущего элемента. Учитывая упорядоченность последних элементов перспективных цепочек, поиск можно сделать дихотомией. При присоединении i-го элемента к какой-нибудь цепочке длины p ее длина увеличивается на 1, a ее последним элементом становится элбмент i. При этом множество S(i+1) совпадает с S(i) за исключением одной цепочки

S(p+1,i+1) = S(p,i) сцепленная с i-ым элементом.

Для хранения цепочек удобно хранить для каждого элемента номер элемента, который ему предшествует в цепочке.

Другое решение этой задачи:

Заведем 3 массива длины N: в массиве A[1..N] помещаются самичисла последовательности. Элемент B[i] имеет значение длины максимальной возрастающей подпоследовательности, завершающейся элементом A[i], а величина C[i] есть индекс предшествующего элементу A[i] элемента вэтой максимальной последовательности (A[i]=0 есть такого элемента нет).

Если N=1, то A[1] и есть искомая подпоследовательность. При этом B[1]=1, C[1]=0. Предположим, что мы заполнили массивы A,B и C от начала до элемента M-1. Попытаемся обработать элемент A[M]. Просматривая массив A от 1 до M-1-го элемента мы ищем такое A[k], что одновременно

2) B[k] максимально.

Очевидно, что для того, чтобы получить максимальную по длине подпоследовательность, заканчивающуюся A[M], этот элемент надо приписать к подпоследовательности с последним элементом A[K]. Получаем, что B[M]=B[K]+1, C[M]=K.

Пусть мы обработали все N элементов массива A. Находим максимальный элемент массива B, пусть это будет B[K]. По построению это длина максимальной подпоследовательности.

Выписываем эту подпоследовательность: полагаем j:=k; печатаем элемент A[j]; так как предшествующий в последовательности элемент имеет индекс C[j], то делаем присваивание j:=C[j], распечатываем этот элемент и т.д., до тех пор, пока j не станет 0 (т.е. мы дошли до начала последовательности).

В программе в переменной Max хранится максимальная найденная до сих пор длина подпоследовательности, в IndexMax находится индекс последнего элемента этой подпоследовательности.

Структура данных, каждый элемент которой (в данном случае A[i]) содержит ссылку (в этой задаче C[i]) на предыдущий элемент (или, если требуется, на последующий элемент) называется однонаправленным списком. Если у элемента есть ссылка как на предыдущий, так и на последующий за ним элемент, то список двунаправленный (его можно реализовать, используя не один массив для индексов, а два).

б). Частный случай пункта в).

в). Заведем матрицу С[0..m+1,1..n]. В ней i-тая строка будет хранить информацию о последовательностях с i-1 разрывами; j-ый элемент в этой строке есть длина самой длинной подпоследовательности элементов «хвоста» массива А ( от j-го элемента до n-го), начинающейся в j-ой позиции и с не более чем i-1 разрывом.

Правило заполнения матрицы:

Заполним нулевую строку нулями (чтобы можно было заполнить первую строку по общему алгоритму).

Для каждого номера строки i от 1 до m+1 выполнить следующие действия:

Для j-го элемента массива A (j изменяется от n до 1) находим максимальную по длине подпоследовательность, которую можно присоединить к этому элементу так, чтобы получить подпоследовательность максимальной длины с не более чем i-1 разрывом. Для этого мы:

1) ищем элемент A[k] последовательности A, больший A[j], стоящий в массиве A правее j-го элемента и с максимальным С[i,k];

2) затем просматриваем элементы i-1 -ой строки матрицы С, начиная с j+1 -го и до конца, и находим C[i-1,s] — максимальный из них;

3) сравниваем C[i-1,s] с С[i,k]. Больший из них (обозначим его C[row,col]), увеличенный на 1, запоминаем в C[i,j]. Это и будет длина максимальной подпоследовательности, начинающейся в позиции j, с не более чем i-1 разрывом.

4) Запоминаем индексы row и col элемента массива C, предшествующего C[i,j], в ячейках X[i,j] и Y[i,j] соответственно.

После окончания цикла максимальный элемент m+1 -ой строки матрицы C и есть максимальная длина возрастающей подпоследовательности с m разрывами. Выписать всю подпоследовательность можно следующим образом: для каждого элемента подпоследовательности в массивах X и Y хранится информация о предшественнике. Мы, начиная с максимального элемента m+1 -ой строки матрицы C, восстанавливаем всю подпоследовательность.

Пусть мы знаем C[i-1,j] для всех j от 1 до n и для некоторого i, а также C[i,k] для k от j+1 до n. Мы хотим вычислить C[i,j].

Для j-го элемента массива А существует максимальная по длине подпоследовательность с не более чем i-1 -им разрывом, начинающаяся с A[j]. Второй элемент (обозначим его A[k]) этой максимальной подпоследовательности (если он, конечно, есть) может быть

1) больше, чем A[j]. Тогда мы находим его среди элементов, обладающих следующими свойствами:

б) C[i,k] максимальный (т.е. мы присоединяем к A[j] максимальную по длине подпоследовательность с не более чем i-1 разрывом, формируя подпоследовательность опять не более чем с i-1 разрывом);

2) меньше или равный, чем A[j]. Тогда мы ищем его среди элементов, обладающих следующими свойствами:

б) C[i-1,k] максимальный (т.е. мы присоединяем максимальную подпоследовательность с не более чем i-2 -мя разрывами, формируя подпоследовательность с не более чем i-1 разрывом).

Полученная подпоследовательность получается максимальной длины, так как длина подпоследовательности, начиная с A[k], максимальная.

Упоминавшиеся выше индексы row и col, которые запоминаются в X[i,j] и Y[i,j] соответственно, обозначают

col — индекс следующего за A[j] элемента в максимальной по длине подпоследовательности, начинающейся в позиции j и имеющей не более i-1 разрыва;

row-1 — максимальное количество разрывов в подпоследовательности, начинающейся в A[col].

Решение задачи 21.

Для решения задачи элементы массива удобно упорядочить по абсолютной величине (в порядке неубывания). Если в массиве есть элементы, равные 0, то один из них и будет последним элементом искомой последовательности, поэтому их можно игнорировать. Пусть К(i) обозначает максимальное количество элементов, которое может находится в некоторой последовательности с требуемым свойством, последним элементом которой является i-й элемент.

Понятно, что наименьшему по абсолютной величине элементу ничего не может предшествовать ни один элемент, поэтому К(р)=0, где р — индекс первого ненулевого элемента.

Для каждого следующего элемента с номером j, j=р+1. N, необходимо определить максимальное количество элементов, которое может предшествовать рассматриваемому элементу, с учетом требуемого свойства. Понятно, что это количество есть максимум из величин К(р 1 ), К(р 2 ). К(р m ), где элементы с номерами p 1 ,p 2 . p m , р 1

Значение К(N), вычисленное по описанному выше правилу, и определяет максимальное количество элементов, которое может находится в некоторой последовательности с требуемым свойством (без учета возможного нуля в конце последовательности).

Для того, чтобы установить, какие элементы образуют максимальную последовательность, достаточно для каждого номера j помнить тот номер из p 1 ,p 2 . p m , на котором достигается максимум для чисел К(p 1 ),К(p 2 ). К(p m ). Эти номера можно определять параллельно с вычислением значения К(j) в некотором массиве, например ПРЕДОК. Используя эту информацию, легко определить номера элементов последовательности, проходя от элемента i с максимальным значением К(i) к элементу, который ему предшествует (ПРЕДОК(i)), до тех пор, пока не придем к первому элементу f последовательности (ПРЕДОК(f)=0).

Решение задачи 22.

Можно, конечно, число A умножить само на себя n-1 раз, но для этого надо выполнить n-1 операцию умножения. Рассмотрим метод, требующий меньшего числа умножений (он, однако, не всегда дает минимальное число умножений).

Если n — четное, n=2m то будем вычислять A n , используя тождество A am =(A m ) 2 ;

если же n=2m+1, то

A 2m+1 =(A 2m )*A=((A m ) 2 )*A.

Так(м образом, возведение A в 13 степень будет выглядеть следующим образом:

(A 13 )=((A 6 ) 2 )*A=(((A 3 ) 2 ) 2 )*A=(((A*A*A) 2 ) 2 )*A

и вычисление требует 5 операций умножения.

Используя данный метод, для возведения в степень n потребуется порядка log 2 (n) операций умножения.

Программа на Паскале может выглядеть так:

Можно ту же самую идею реализовать и по другому ( далее мы приводим выдержку из книги Д.Кнута «Искусство программирования для ЭВМ», т.2, с.482):

«Запишем n в двоичной системе счисления и заменим в этой записи каждую цифру «1» парой букв SX, а каждую цифру «0» — буквой S, после чего вычеркнем крайнюю левую пару букв SX. Результат, читаемый слева направо, превращается в правило вычисления x n , если букву «S» интерпретировать как операцию возведения в квадрат, а букву «X» — как операцию умножения на x. Например, если n=23, то его двоичным представлением будет 10111; строим последовательность SX S SX SX SX, удаляем из нее начальную пару SX и в итоге получаем следующее правило вычисления: S SX SX SX. Согласно этому правилу, мы должны «возвести x в квадрат, затем снова возвести в квадрат, затем умножить на x, возвести в квадрат, умножить на x, возвести в квадрат и, наконец, умножить на x»; при этом мы последовательно вычисляем x 2 , x 4 , x 5 , x 10 , x 11 , x 22 , x 23 .

Этот «бинарный метод» легко обосновать, рассмотрев последовательность получаемых в ходе вычисления показателей: если «S» интерпретировать как операцию умножения на 2, а «X» — как операцию прибавления 1 и если начать с 1, а не с x, то наше правило дает нам в соответствии со свойствами двоичной системы счисления число n».

Приведенный метод не дает минимального числа операций умножения. Для вычисления x 23 нам, по изложенному выше методу, потребуется 7 операций умножения. В действительности их необходимо только 6:

x -> x 2 -> x 3 -> x 5 -> x 10 -> x 20 -> x 23 .

Алгоритм нахождения минимального числа операций (кроме полного перебора) сейчас неизвестен (см. там же у Д.Кнута).

Решение задачи 23.

Пусть z есть массив из N элементов, y — из M. Положим i=1 и j=1. Берем элемент z[i] и ищем минимальное k, k>=j, k

Решение задачи 24.

Пусть x=x 1 ,x 2 , . ,x m , y=y 1 ,y 2 , . ,y n .

Заведем матрицу A[0..m,0..n]. Элемент A[i,j] будет длиной

максимальной общей подпоследовательности y x 1 , . ,x i и y y 1 , . y j . Сначала A[i,0]=A[0,j]=0, i=0, . ,m, j=0, . ,n.

Пусть x i =y j , тогда требуется увеличить длину максимальной общей подпоследовательности x 1 , . ,x i-1 и y 1 , . ,y j-1 на 1: A[i,j]=A[i-1,j-1]+1, если x i =y j .

В случае, если x i y j , то, очевидно,

но так как всегда

A[i-1,j-1] i и y i — это последние общие совпадающие элементы в x и y.

Начиная от элемента A[i-1,j-1] повторяем, как было описано выше, движение влево и вверх по матрице, находим предпоследний совпадающий элемент в x и y, и т.д.

Решение задачи 25.

В последовательностях x и y избавляемся от лидирующих нулей. Если хоть одна из последовательностей стала пустой, то z=0. Иначе крайние левые цифры и в x и в y есть 1.

Запускаем на полученных последовательностях алгоритм задачи 24 (для получения максимального z необходимо, чтобы старшая цифра z была 1 и двоичная запись z имела максимальную длину), но при этом для каждого A[i,j] — длины последовательности, необходимо хранить добавочно и саму последовательность; при присвоении значения A[i,j] одновременно будем запоминать и последовательность максимальной длины. Если таких несколько, то берем из них последовательность с максимальным значением. Поэтому алгоритм задачи 23 запишется так:

Пусть S[0..m,0..n] — массив строк. В S[i,j] будет храниться подпоследовательность, длина которой A[i,j].

Попробуйте не заводить массив S[0..m,0..n], а обойтись одномерным массивом S[0..n].

Видео:R-1 Рекуррентные соотношения: введениеСкачать

Динамическое программирование. Принцип Беллмана. Основное рекуррентное соотношение Беллмана. Общие принципы решения задач динамического программирования.

1.Динамическое программирование в теории управления и теории вычислительных систем — способ решения сложных задач путём разбиения их на более простые подзадачи. Он применим к задачам с оптимальной подструктурой (англ.), выглядящим как набор перекрывающихся подзадач, сложность которых чуть меньше исходной. В этом случае время вычислений, по сравнению с «наивными» методами, можно значительно сократить.

Ключевая идея в динамическом программировании достаточно проста. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико.

Метод динамического программирования сверху — это простое запоминание результатов решения тех подзадач, которые могут повторно встретиться в дальнейшем. Динамическое программирование снизу включает в себя переформулирование сложной задачи в виде рекурсивной последовательности более простых подзадач.

Оптимальная подструктура в динамическом программировании означает, что оптимальное решение подзадач меньшего размера может быть использовано для решения исходной задачи. К примеру, кратчайший путь в графе из одной вершины (обозначим s) в другую (обозначим t) может быть найден так: сначала считаем кратчайший путь из всех вершин, смежных с s, до t, а затем, учитывая веса ребер, которыми s соединена со смежными вершинами, выбираем лучший путь до t (через какую вершину лучше всего пойти). В общем случае мы можем решить задачу, в которой присутствует оптимальная подструктура, проделывая следующие три шага.

Разбиение задачи на подзадачи меньшего размера.

Нахождение оптимального решения подзадач рекурсивно, проделывая такой же трехшаговый алгоритм.

Использование полученного решения подзадач для конструирования решения исходной задачи.

Подзадачи решаются делением их на подзадачи ещё меньшего размера и т. д., пока не приходят к тривиальному случаю задачи, решаемой за константное время (ответ можно сказать сразу). К примеру, если нам нужно найти n!, то тривиальной задачей будет 1! = 1 (или 0! = 1).

Перекрывающиеся подзадачи в динамическом программировании означают подзадачи, которые используются для решения некоторого количества задач (не одной) большего размера (то есть мы несколько раз проделываем одно и то же). Ярким примером является вычисление последовательности Фибоначчи, и — даже в таком тривиальном случае вычисления всего двух чисел Фибоначчи мы уже посчитали дважды. Если продолжать дальше и посчитать , то посчитается ещё два раза, так как для вычисления будут нужны опять и . Получается следующее: простой рекурсивный подход будет расходовать время на вычисление решение для задач, которые он уже решал.

Чтобы избежать такого хода событий мы будем сохранять решения подзадач, которые мы уже решали, и когда нам снова потребуется решение подзадачи, мы вместо того, чтобы вычислять его заново, просто достанем его из памяти. Этот подход называется кэширование. Можно проделывать и дальнейшие оптимизации — например, если мы точно уверены, что решение подзадачи нам больше не потребуется, можно выкинуть его из памяти, освободив её для других нужд, или если процессор простаивает и мы знаем, что решение некоторых, ещё не посчитанных подзадач, нам понадобится в дальнейшем, мы можем решить их заранее.

Подводя итоги вышесказанного можно сказать, что динамическое программирование пользуется следующими свойствами задачи:

возможность запоминания решения часто встречающихся подзадач.

Динамическое программирование обычно придерживается двух подходов к решению задач:

нисходящее динамическое программирование: задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи. Используется запоминание для решений часто встречающихся подзадач.

восходящее динамическое программирование: все подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи. Этот способ лучше нисходящего программирования в смысле размера необходимого стека и количества вызова функций, но иногда бывает нелегко заранее выяснить, решение каких подзадач нам потребуется в дальнейшем.

Языки программирования могут запоминать результат вызова функции с определенным набором аргументов (мемоизация), чтобы ускорить «вычисление по имени». В некоторых языках такая возможность встроена (например, Scheme, Common Lisp, Perl), а в некоторых требует дополнительных расширений (C++).

Известны сериальное динамическое программирование, включённое во все учебники по исследованию операций, и несериальное динамическое программирование (НСДП), которое в настоящее время слабо известно, хотя было открыто в 1960-х годах.

Обычное динамическое программирование является частным случаем несериального динамического программирования, когда граф взаимосвязей переменных — просто путь. НСДП, являясь естественным и общим методом для учета структуры задачи оптимизации, рассматривает множество ограничений и/или целевую функцию как рекурсивно вычислимую функцию. Это позволяет находить решение поэтапно, на каждом из этапов используя информацию, полученную на предыдущих этапах, причём эффективность этого алгоритма прямо зависит от структуры графа взаимосвязей переменных. Если этот граф достаточно разрежен, то объём вычислений на каждом этапе может сохраняться в разумных пределах.

Одним из основных свойств задач, решаемых с помощью динамического программирования, является аддитивность. Неаддитивные задачи решаются другими методами. Например, многие задачи по оптимизации инвестиций компании являются неаддитивными и решаются с помощью сравнения стоимости компании при проведении инвестиций и без них.

2. Принцип Беллмана

Принцип оптимальности Беллмана (также известный как принцип динамического программирования), названный в честь Ричарда Эрнста Беллмана, описывает действие математического метода оптимизации, называемого динамическим программированием. Он заключается в том, что на каждом шаге следует стремиться не к изолированной оптимизации функции fk(хk, ξk), а выбирать оптимальное управление хk* в предположении об оптимальности всех последующих шагов.

Принцип оптимальности: оптимальная стратегия имеет свойство, что какими бы ни были начальное состояние и начальное решение, последующие решения должны составлять оптимальный курс действий по отношению к состоянию, полученному в результате первого решения.

Беллмана принцип оптимальности

БЕЛЛМАНА ПРИНЦИП ОПТИМАЛЬНОСТИ [Bellman’s optimality principle] — важнейшее положение динамического программирования, которое гласит: оптимальное поведение в задачах динамического программирования обладает тем свойством, что каковы бы ни были первоначальное состояние и решение (т. е. “управление”), последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения. Этот принцип можно выразить и рассуждая от противного: если не использовать наилучшим образом то, чем мы располагаем сейчас, то и в дальнейшем не удастся наилучшим образом распорядиться тем, что мы могли бы иметь.

Следовательно, если имеется оптимальная траектория, то и любой ее участок представляет собой оптимальную траекторию. Этот принцип позволяет сформулировать эффективный метод решения широкого класса многошаговых задач. (Подробнее см. Динамическое программирование.)

Принцип назван по имени крупного американского математика Р. Беллмана, одного из основоположников динамического программирования.

Принцип Беллмана позволяет упростить нахождение оптимальных стратегий. [1]

Принцип Беллмана для задачи управления со многими критериями формулируется в виде следующей теоремы. [2]

Уравнение ( 55) выражает принцип Беллмана в задаче об оптимальной остановке. [3]

В § 2 сформулирован многокритериальный аналог принципа Беллмана. В § 3 рассмотрена задача независимого выбора; в § 4 — задача конструирования. [4]

Так как по условию на всех уровнях дихотомические деления выполняются оптимально и оптимизируемые параметры аддитивны, при построении конечного сечения обеспечивается выполнение принципа Беллмана, поэтому достигнутое сечение является оптимальным и все КТС, приписанные этим узлам, составляют оптимальный типаж обслуживающей системы. [5]

Так как задача оптимизации типажа аддитивна и затраты на построение оптимального типажа состоят из суммы затрат на серии отдельных оптимальных типоразмеров, к решению может быть применен принцип Беллмана. По определению, каждый узел, через который проходит оптимальное сечение, является также оптимальным сечением соответствующего субграфа, приписанного данному узлу. При этом оптимальное сечение субграфа, подчиненного узлу, лежащему на оптимальном сечении полного графа, проходит через его вершину. Таким образом, геометрическое место вершин оптимальных субграфов является оптимальным сечением графа альтернативных решений. Следовательно, типаж, представленный оптимальным сечением графа альтернативных решений, может обслужить весь портфель заявок при минимальных затратах на обслуживание. [6]

Вывод необходимых условий оптимальности производится на. Предварительно заметим, что по принципу Беллмана [2] любой участок оптимальной траектории также должен быть оптимальной траекторией. [7]

Для выбора критериев при использовании концепции оптимизации применяют различные принципы оптимальности. Например, при исследовании систем в определенных условиях часто используют принцип Беллмана или принцип максимума Понтря-гина. При наличии случайных факторов используют принцип наибольшего среднего результата или принцип наибольшего гарантированного результата. Принцип наибольшего гарантированного результата при учете неопределенностей, связанных с наличием несовпадающих интересов ( например, в конфликтных ситуациях), приводит, в частности, к принципу максимина. [8]

Каждое из этих управлений по формуле ( 4) приводит к доходу Jn ( x0, и): 0, 3, 2, 1, 1, 2, 3, 0 соответственно. Доход 3, 0 при управлении ( ы2, [ и4) мажорирует остальные доходы. В силу задания единственным ( х0, R, 2) — оптимальным является управление ( 2, J. Таким образом, в рассмотренной задаче со специально выбранным отношением R принцип Беллмана не выполняется. [9]

Достроенный таким образом граф снизу до верха можно сопоставить с графом, полученным методом сверху вниз путем дихотомии, и произвести коррекцию обоих вариантов с целью исключения ошибки ( см. гл. Напомним, что при практическом использовании метода оптимальных дихотомий возможна ошибка за счет неточной аналитической аппроксимации интегральных стоимостных характеристик. Коррекция позволяет исключить и эти ошибки. В этом случае, оптимальное сечение полного графа предлагается искать в соответствии с принципом Беллмана, для чего доказывается следующая теорема

Дата добавления: 2015-09-10 ; просмотров: 71 | Нарушение авторских прав

📺 Видео

Динамическое программирование: траектории кузнечикаСкачать

Рекуррентные соотношения. Часть 1. Молодечно 2022.Скачать

АиСД S01E10. Динамическое программированиеСкачать

Динамическое программирование — это просто | Скринкасты | Академия данных MADE | #1Скачать

Принцип оптимальности БеллманаСкачать

Задача из Собеседования в Google на Динамическое Программирование: Количество Уникальных ПутейСкачать

Семинар 3. Динамическое программирование (Алгоритмы и структуры данных, часть 1)Скачать

21.04 - дискра, рекуррентные соотношенияСкачать

Основные алгоритмы 12. Динамическое программирование IСкачать

План решения задачи методом динамического программирования. Центр онлайн-обучения «Фоксфорд»Скачать

Динамическое программированиеСкачать

АиСД S01E10. Динамическое программированиеСкачать

Решение неоднородного рекуррентного уравненияСкачать

Лекция 4. Динамическое программирование 1Скачать

ДМ 1 семестр 12 лекция: Подсчет КО и рекуррентные соотношенияСкачать

Алгоритмы динамическое программирование [GeekBrains]Скачать

Информатика. Двумерное динамическое программирование: игры. Центр онлайн-обучения «Фоксфорд»Скачать

Тренировки по алгоритмам 3.0. Лекция 3: «Динамическое программирование с одним параметром»Скачать