В этом разделе вы найдете бесплатные примеры решений рекуррентных соотношений методом характеристического уравнения и подбора частного решения по правой части. Также приведены краткие алгоритмы решения для двух методов и пример их использования для последовательности Фибоначчи.
- Как решать рекуррентные соотношения?
- Метод производящих функций
- Метод характеристических функций
- Решение для последовательности чисел Фибоначчи
- Способ 1. Производящяя функция
- Способ 2. Характеристическое уравнение
- Примеры решений
- Курсовая работа по теме»Методы решения рекуррентных соотношений.Рекуррентные соотношения в школьном курсе математики»
- Оглавление
- Введение
- 1. Методы решения рекуррентных соотношений
- 1.1 Понятие рекуррентной формулы
- 1.2 Методы решения рекуррентных соотношений
- 1.2.1 Метод математической индукции
- 1.2.2 Метод итерации (подстановки)
- 1.2.3 Метод производящих функций
- 1.2.4 Методы решения линейных однородных рекуррентных соотношений
- 1.2.5 Методы решения линейных неоднородных рекуррентных соотношений
- 2. Рекуррентные соотношения в школьном курсе математики
- 2.1 Числовая последовательность
- 2.2 Арифметическая прогрессия
- 2.3 Геометрическая прогрессия
- 2.4 Практические задачи (из школьного курса математики)
- Заключение
- Дискретная математика — рекуррентное соотношение
- Определение
- Линейные рекуррентные отношения
- Как решить линейное рекуррентное соотношение
Видео:9. Решение рекуррентных соотношений. Дискретная математика.Скачать

Как решать рекуррентные соотношения?
Для решения рекуррентных соотношений применяют один из двух основных способов:
- Метод производящих функций
- Метод характеристического уравнения
В следующем разделе мы сравним, как выглядит процесс решения для одной и той же последовательности двумя методами.
Метод производящих функций
- Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен $k$) $$a_ = …, \ a_ = …, \ a_ = …, \ … \ a_ = …, ngeqslant k$$
- Домножить каждую строчку на $z$ в соответствующей степени $z^ cdot a_$ и сложить все выражения для $n ge 0$. В левой части получится сумма $displaystylesum_^ a_nz^n$ — это производящая функция, назовем ее $G(z)$. Правую часть преобразовать так, чтобы она превратилась в выражение, включающее $G(z)$.
- Решить полученное уравнение относительно $G(z)$.
- Разложить $G(z)$ в степенной ряд, тогда коэффициент при $z_n$ будет искомым выражением для $a_n$.
Метод характеристических функций
Этот метод практически полностью аналогичен методу решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, кратко алгоритм выглядит так:
- Записать соответствующее однородное рекуррентное уравнение (РУ): $$ p_ a_ + p_a_ + . + p_n a_n =f to \ to p_ a_ + p_a_ + . + p_n a_n =0. $$
- Выписать для него характеристическое уравнение и найти его корни $lambda_i$ $$ p_ lambda^ + p_lambda^ + . + p_lambda + p_n =0. $$
- Выписать согласно полученным корням $lambda_1, . lambda_k$ общее решение однородного рекуррентного соотношения (подробнее теорию см. по ссылке [1] ниже). $$ C_1 lambda_1^n +. +C_k lambda_k^n , mbox , $$ $$ C_1 lambda_1^n + C_2 nlambda_1^n +. +C_m n^m lambda_1^n+. +C_k lambda_k^n mbox , lambda_1 , , m. $$
- Подобрать частное решение неоднородного рекуррентного соотношения по виду правой части (особенно удобно для правых частей вида $mu^n*P(n)$, $P(n)$ — многочлен от $n$).
- Представить общее решение неоднородного РУ как сумму общего решения соответствующего однородного РУ и частного решения неоднородного РУ.
- Подставить начальные условия $a_0, a_1, . a_$ и получить значения констант $C_1, . C_k$.
Видео:Решение рекуррентных уравненийСкачать

Решение для последовательности чисел Фибоначчи
Последовательность чисел Фибоначи — это последовательность, каждый элемент которой (кроме нулевого и первого) равен сумме двух предыдущих:
$$ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 , . $$
Числа Фибоначчи растут быстро: $f_=55$, $f_=6765$, а $f_=354224848179261915075$.
Общая формула данной рекуррентной последовательности имеет вид6
Способ 1. Производящяя функция
Начинаем с второго шага алгоритма, домножаем на $z^n$:
$$begin 1cdot f_0 &= &0cdot 1,\ zcdot f_1 &= &1cdot z,\ zcdot f_n & = &(f_+f_)cdot z^n, quad ngeq2.\ end $$
Складываем все строчки:
На третьем шаге алгоритма приводим все суммы к замкнутому виду:
откуда выводим искомое выражение для производящей функции:
Теперь разложим ее в степенной ряд. Для этого сначала разложим знаменатель на множители. Найдем корни уравнения:
Чтобы разложить данные дроби в ряды, используем известное разложение для дроби:
Рассмотрим первую дробь и поделим в ней числитель и знаменатель на $z_1$:
Аналогично (но с делением на $z_2$) действуем со второй дробью:
Преобразуем данное выражение, используя то, что
$$1/z_1=-z_2, quad 1/z_2 = -z_1, quad z_1-z_2=sqrt $$ $$f_n=frac<sqrt>left( biggl( frac<1+sqrt> biggr)^n — biggl( frac<1-sqrt> biggr)^n right). $$
Способ 2. Характеристическое уравнение
Запишем характеристический многочлен для $f_n=f_+f_$, и найдем его корни:
Тогда общее решение однородного рекуррентного уравнения имеет вид:
Осталось найти значения произвольных постоянных $C_1, C_2$ из начальных условий $f_0=0, f_1=1$.
Решая систему, найдем
Итоговое выражение для последовательности чисел Фибоначчи:
Результаты обоих методов совпали, решение вторым методом оказалось проще и короче.
Видео:21.04 - дискра, рекуррентные соотношенияСкачать
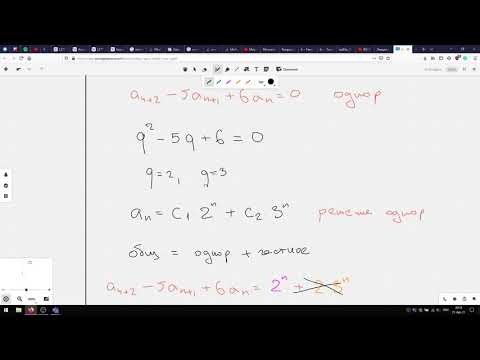
Примеры решений
Задача 1. Решить рекуррентное соотношение $f(n+2)=-6f(n+1)+7f(n)+n-3$ с начальными условиями $f(0)=2$ и $f(1)=4$, сделать проверку
Задача 2. Решить рекуррентное соотношение $f(n+2)=-2f(n+1)+3f(n)-3^n$ с начальными условиями $f(0)=1$, $f(1)=3$ и сделать проверку
Задача 3. 1. Решить рекуррентное соотношение $f(n+2) =-5f(n+1) -4f(n) + 3n^2$ с начальными условиями $f(0) = 2$, $f(1) = 3$.
2. Проверить, удовлетворяет ли найденное решение начальным условиям и обращает ли оно рекуррентное соотношение в справедливое тождество.
Задача 4. Найти последовательность $$, удовлетворяющую рекуррентному соотношению $a_ + 4 a_ + 3 a_ = 0$ и начальным условиям $a_1=2$, $a_2=4$.
Видео:Решение неоднородного рекуррентного уравненияСкачать

Курсовая работа по теме»Методы решения рекуррентных соотношений.Рекуррентные соотношения в школьном курсе математики»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Уральский государственный педагогический университет»
Институт математики, физики, информатики и технологий
Кафедра высшей математики и методики обучения математике
Методы решения рекуррентных соотношений. Рекуррентные соотношения в школьном курсе математики.
Направление подготовки «Педагогическое образование: математика»
Допущена к защите
Работа защищена на оценку
Холкина Е.И. – студентка
группы МАТ – 1601 Z
Бондарь А.А. – кандидат физико-математических наук, доцент кафедры высшей математики и методики обучения математике
Видео:Рекуррентные уравненияСкачать

Оглавление
Видео:Понятие о рекуррентных соотношениях и производящих функцияхСкачать

Введение
Для полной картины понимания проводимого исследования, отметим что такое рекурсия — это свойство объекта подражать самому себе. Это означает, что объект является рекурсивным в том случае, если его части выглядят также как весь объект. Рекурсия очень широко применяется в математике и программировании, что в процессе работы над курсовой мы исследуем в специфике рекуррентных соотношений, а именно м етодов решения рекуррентных соотношений и их изучения в школьном курсе именно математики.
Актуальность темы работы определяет то, что рекуррентные соотношения изучаются в различных разделах математики, в том числе и прикладной: теории сложности алгоритмов, вычислительных методах и теории вероятностей, комбинаторике, и тем не менее, еще есть вопросы, которые требуют более детального изучения, что немаловажно для дальнейшего использования в науке и работе преподавателей.
В результате многочисленных исследований и практических трудов специалистов было доказано, что не существует определенно одного метода, который позволяет решать все рекуррентные соотношения. Однако, учеными были установлены несколько методов, которые позволяют решать ряд рекуррентных соотношений. На них мы и остановимся в курсовой.
Методом сведения данной задачи к задаче, касающейся меньшего числа предметов часто пользуются при решении многих комбинаторных задач. Методом рекуррентных соотношений называют метод сведения к аналогичной задаче для меньшего числа предметов. Можно свести задачу об n -предметах к задаче n 1 предметах, потом к задаче об n 2 и т.д., пользуясь рекуррентными соотношениями. Таким образом, последовательно уменьшая число предметов, доходим до задачи, которую уже легко решить.
Предмет исследования – методы решения рекуррентных соотношений и их применение в школьном курсе математики.
Объектом являются — рекуррентные соотношения.
Целью работы является исследование методов решения рекуррентных соотношений.
Для достижений цели работы необходимо решить ряд поставленных задач:
— определить понятие рекуррентных соотношений;
— исследовать научно-методическую литературу по данной теме;
— систематизировать найденный материал и отметить особенности;
— изучить особенности методов рекуррентных соотношений;
— определить, где в школьном курсе математики изучают рекуррентные соотношения и исследовать их.
Курсовая работа состоит из введения, двух глав с подпунктами, заключения и списка использованных источников.
Видео:Рекуррентное вычисление определителя порядка nСкачать

1. Методы решения рекуррентных соотношений
Видео:Лекция 4. Рекуррентные соотношенияСкачать

1.1 Понятие рекуррентной формулы
Возможность использования метода математической индукции при решении более сложных по восприятию задач, если говорить точнее — рекуррентных соотношений, ведет к необходимости его развития.
Согласно определению, рекурр е нтная ф о рмула (от латинского recurrens, родительный падеж recurrentis возвращающийся) – это так называемая формула приведения, то есть та формула, которая сводит вычисление nго члена какойлибо последовательности (чаще числовой) к вычислению нескольких предыдущих её членов. 1
Обычно данные члены находятся в рассматриваемой последовательности «недалеко» от её nго члена, число их от n не зависит и nй член через них выражается просто. Предметом теории рекурсивных функций является общая проблематика рекуррентных вычислений.
Рекуррентное соотношение или рекуррентную формулу определяют как соотношение вида a n + k = F ( n, a n , a n +1 ,…,a n + k -1 ), который позволяет вычислить все члены последовательности, при условии, что заданы ее первые k члены.
Итак, наличие рекуррентного соотношения и начальных условий позволяет нам последовательно, шаг за шагом, определить любое наперед заданное количество n членов рекуррентной числовой последовательности. Зачастую это все, что нам требуется от задачи; иными словами, получение рекуррентного соотношения для искомой числовой последовательности an является вполне приемлемым, а зачастую — и наиболее удобным с вычислительной точки зрения ответом поставленной задачи.
Однако иногда нам хочется получить явное аналитическое выражение для общего члена a n этой последовательности, или, как говорят, решить данное рекуррентное соотношение.
Далее перейдем к методам решения рекуррентных соотношений.
Видео:05 Рекуррентные соотношенияСкачать

1.2 Методы решения рекуррентных соотношений
Решение рекуррентных соотношений представляет собой несколько методов. В пределах данной части исследования рассмотрим следующие из них:
— метод математической индукции,
— метод итерации (подстановки),
— метод производящих функций
— метод решения однородных и неоднородных рекуррентных соотношений.
Рассмотрим выбранные методы детально.
Видео:R-1 Рекуррентные соотношения: введениеСкачать

1.2.1 Метод математической индукции
П оследовательность чисел или функций, где каждый следующий член выражается через предыдущий, называется рекуррентной, формулы, устанавливающие эту связь, — это рекуррентные соотношения.
Метод рекуррентных соотношений — полный аналог метода математической индукции, при котором начальное значение вычисляемой величины — база индукции, а рекуррентное соотношение — шаг индукции. 2
При условии, когда рекуррентное соотношение линейно и однородно, т.е. выполняется соотношение вида:
Видео:Алгоритмы теория и практика Методы - 100 урок. Рекуррентные соотношенияСкачать

1.2.2 Метод итерации (подстановки)
Метод итерации или подстановки стоит отметить как важный метод решения, сущность которого в следующем. К примеру, дано уравнение:
Где f(x) – непрерывная функция, требуется определить его вещественные корни. Заменяем уравнение (1) равносильным:
Далее, следует выбрать каким-либо из способом приближенное значение корня x 0 , которое подставляем в правую часть(2) и получаем некоторое число
Повторяя этот процесс, имеем последовательность:
Если эта последовательность – сходящаяся, т.е. существует предел , то, переходя к пределу в равенстве (4) и предполагая функцию j (x) непрерывной, найдем:
Следовательно, предел — это корень уравнения (2) и может быть вычислен по формуле (4) с любой степенью точности.
Доказано, что выполнение условия: | j (x) | 1 для x [ a, ,b ] -достаточное условие сходимости итерационного процесса, при котором он сходится к единственному корню . На рис. 1 — пример сходящегося итерационного процесса x n+1 =j (x n ) при | j(x)| 1, а на рис. 2 – расходящегося при | j (x) | 1.
Итерационный метод подходит для решения рекуррентных уравнений первого порядка.
Видео:Определитель Вандермонда. Метод рекуррентных соотношенийСкачать

1.2.3 Метод производящих функций
Понятие производящей функции — это одно из основных понятий современной перечислительной комбинаторики. Задача этого пункта — дать вначале неформальное, а затем и вполне строгое определение этой функции. Согласно определению, каждая производящая функция является элементом кольца формальных степенных рядов. Следовательно, любую пару производящих функций можно складывать и перемножать между собой.
Рассмотрим метод решения задач с помощью производящих функций.
Суть метода: сопоставим некоторой последовательности g 0 , g 1 , g 2 , . g n — дискретному объекту, степенной ряд g 0 + g 1 z + g 2 z 2 +… + g n z n +… — объект непрерывный, тем самым подключаем к решению задачи средства математического анализа. 4
Последовательность генерируется, если порождается производящей функцией. На самом деле, это символьная конструкция, где вместо символа z может быть любой объект, для которого определены операции сложения и умножения.
Согласно изученных материалов, начало методу производящих функций положил известный английский математик Абрахам де Муавр, а продолжил его дальнейшее исследование и развитие — Леонард Эйлер. Леонард в 50-х годах XVIII века решал задачу: какие грузы можно взвесить с помощью гирь в 2 0 , 2 1 , 2 2 . 2 n грамм и сколькими способами? Он посчитал необходимым использовать для решения метод производящих функций , еще неизвестный в то время.
Алгоритм решения примерно такой: рассматривается некоторая бесконечная сумма, в конечном итоге представляющая собой формальный степенной ряд G(z) = g 0 + g 1 z + g 2 z 2 +… + g n z n + … , где коэффициенты g k (не заданные в явном виде) — ключ к решению задачи. Z является просто символом и вместо него может быть любой объект: шар, число, кость домино и т.д., что показывает то, что сам ряд является формальным.
В отличие от степенных рядов в анализе формальным степенным рядам не придается числовых значений и, как итог, не имеет смысла говорить о сходимости таких рядов для числовых представленных аргументов.
Отметим, что хотя G(z) — функция, это всё-таки формальная запись, поэтому нельзя подставить вместо z любое значение z = z 0 , за исключением z = 0 , так как G(0) = g 0 . 5
Бесконечную сумму G(z) мы преобразуем к замкнутому (компактному) виду. У производящей функции есть бесконечное и замкнутое представления. Необходимо бесконечный вид преобразовать к замкнутому, а затем замкнутый вид разложить в степенной ряд, тем самым получить значения для коэффициентов g k , что необходимо сделать для решения задачи. Метод связан с возможностью записать производящую функцию в замкнутом виде.
Например, производящая функция для последовательности 1, 1, 1, . 1 в бесконечном виде представляется как 1 + x + x 2 + x 3 + . а в замкнутом — .
С помощью производящих функций можно решать рекуррентные соотношения. Например, последовательность чисел Фибоначчи. Числа Фибоначчи определяются рекуррентным выражением, т.е. таким, что вычисление элемента которого выражается из предыдущих элементов.
Формула в замкнутом виде содержит иррациональное число («золотое сечение») в своём составе. Итак, имеем:
Каждую строчку умножаем на z 0 , z 1 . z n, соответственно:
Суммируем эти равенства :
Обозначаем левую часть:
Далее, рассмотрим каждое из слагаемых в правой части:
Получаем уравнение G(z) = z + z G(z) + z 2 G(z), в результате решения которого относительно G(z) находим G ( z ) = – производящая функция для последовательности чисел Фибоначчи.
Разложим её на сумму простейших дробей. А для этого необходимо найти корни уравнения 1 z z 2 =0 . Это простое квадратное уравнение, в результате решения которого получаем:
Следовательно, нашу производящую функцию можно разложить следующим образом:
На следующем этапе находим коэффициенты a и b, умножая дроби на общий знаменатель:
Подставляем в это уравнение значение z = z 1 и z = z 2
Далее, преобразуем выражение для производящей функции:
Теперь каждая из дробей представляет собой сумму геометрической прогрессии. Теперь, по формуле:
Но требовалось найти G(z) в виде:
Отсюда делаем вывод, что:
Эту формулу можно переписать в другом виде, не используя «золотое сечение»:
Видео:Линейные рекуррентные соотношения || Гущин Д. Д.Скачать

1.2.4 Методы решения линейных однородных рекуррентных соотношений
Метод, который использует характеристический многочлен рекуррентного соотношения, рассматривают для решения линейных однородных рекуррентных соотношений. Общее решение линейного рекуррентного соотношения зависит от того, являются ли корни характеристического многочлена действительными (равными или различными) или мнимыми. 6
Пойдем методом от простого к сложному. Наиболее простым является линейное уравнение с постоянными коэффициентами:
где (далее ), а — заданная функция.
Если , то заменой уравнение (1) превращается в уравнение ( n -1)- го порядка. Поэтому, положим . Функцию , определенную в некоторой области будем считать интегрируемой достаточное число раз. Где, , считаем , а — заданная функция.
Запись решения в такой форме, когда любое решение уравнения будет частным случаем этой формы составляет суть общего решения (1). При добавлении любого решения y 0 однородного уравнения вид общего решения не должен измениться:
Следовательно, общее решение уравнения (1) складывается из любого частного решения этого уравнения и линейной комбинации решений однородного уравнения (2). Отметим, что
является решением уравнения (2), если удовлетворяет уравнению
Обозначая через — корни алгебраического уравнения (4), уравнение (1) можно записать в виде:
где есть оператор производной:
Оператор I (, обратный оператору () , имеет следующий смысл:
Если в (6) сделать замену то получим
где — произвольные константы, причем, если , то можно положить .
Действуем последовательно на обе части уравнения (5) обратными операторами (в любом порядке):
(тут — константы, причем , как и ).
К решению (8) можно прибавить любое решение уравнения (2), записываем в общем виде:
где — константы, а — набор линейно независимых решений уравнения (2). Если все корни различные, то эти решения имеют вид (3), т.е.
При кратности корней этот набор видоизменяется. Таким образом, если корень имеет кратность k , то ему соответствуют решения:
где k 1 кратность корня , причем
Стоит отметить, что решение вида (10) автоматически получается из (8), если в последнем считать, что Однако, стоит записывать общее решение уравнения (1) в виде суммы решений (8) и (9):
Здесь из (2 n +1) констант и c лишь n констант являются независимыми. Т.е. (11), в конечном счете, будет иметь вид:
где константы — определенные функциями константы, содержащихся в (11).
Если использовать данное решение в аналитических выкладках, то удобнее считать, что (т.е. ограничиться решением ( 8 ).
Например, для нахождении решения с начальными условиями (2), где можно положить, что:
арассчитывать из системы линейных уравнений
Отметим, что решение (8) в действительности x = x 0 не зависит от порядка, в котором пронумерованы корни. Однако интегрирование упрощается, если номера кратных корней следуют друг за другом.
В случае вещественности уравнения (1) комплексные корни уравнения (4) попарно сопряжены. Поэтому, подходящим подбором констант решение уравнения (1) можно записать в действительной форме, при этом бывает удобнее пользоваться комплексным решением, сокращая в два раза число констант.
Видео:Рекуррентное уравнениеСкачать

1.2.5 Методы решения линейных неоднородных рекуррентных соотношений
Структура общего решения линейного неоднородного рекуррентного соотношения аналогична структуре общего решения линейных дифференциальных уравнений с постоянными коэффициентами. Общее решение неоднородного линейного рекуррентного соотношения равно сумме общего решения линейного однородного рекуррентного соотношения и частного решения неоднородного соотношения. Структура частного решения зависит от того, входит ли свободный член неоднородного соотношения в общее решение однородного соотношения.
Рассмотрим неоднородное линейное рекуррентное уравнение:
N = 0, 1, 2, …, коэффициенты – это заданные постоянные, причём , а – заданная функция n . Для задания начальных условий фиксируем значения .
Предположим — одно решение уравнения найдено. Это решение будем считать частным, обозначив через .
Второй член в левой части последнего равенства равен правой части, следовательно,
Таким образом, это обозначает, что является решением однородного линейного рекуррентного уравнения, которое соответствует о = 0.
Поэтому, если найдено частное решение — можно найти общее решение однородного рекуррентного уравнения. После чего по начальным условиям можно определить неопределённые коэффициенты.
Для некоторых функций частное решение находят достаточно просто. Так, в случае если , где – константа, то частным решением является
где – характеристический многочлен.
Докажем, п одставляя , где с – постоянная, в неоднородное рекуррентное уравнение, получаем .
Отсюда следует формула (1).
Например, нужно найти решение уравнения:
с начальными условиями .
Уравнение имеет характеристический многочлен . Если бы правая часть уравнения была равна, то частным решением было бы . Для соответствующее частное решение
По начальным условиям: , ,
Если – многочлен от n степени k и единица не является характеристическим корнем рекуррентного уравнения, т.е . , то частное решение следует искать:
Подставляя этот многочлен в неоднородное рекуррентное уравнение, получаем:
Так как то, сравнивая коэффициенты при высших степенях в левой и правой частях последнего равенства, можно определить значение, и последовательно коэффициенты
Допустим, необходимо решение уравнения:
с начальным условием .
Характеристический многочлен находим следующим образом:
Если , то k = 1, а значит.
Отсюда следует, что Из начального условия находим ḟ n .
Видео:Алгебра 9 класс. Рекуррентный способ задания числовой последовательности. Примеры.Скачать

2. Рекуррентные соотношения в школьном курсе математики
Такие термины как «рекурсивные функции», «рекуррентные последовательности» и «рекуррентные соотношения» в математике употребляют часто. Несмотря на некоторые различия в названии – все они имеют единый корень, который идет еще от латинского гесиггеге, что означает возвращаться. Кроме этого, общим является то, что для получения вычисления очередного значения функции, к примеру, либо реализации алгоритма, либо определения очередного члена последовательности – надо обратиться к их предшествующим значениям, которые были вычислены ранее. Соответственно, для вычисления предшествующих значений требуется обращение к вычисленным перед этим требуемым значениям и так далее.
Таким образом, было выделено правило определения способа вычисления очередного значения функции или очередного члена последовательности, учитывая, что эти значения известны для первого шага. Правило это получило название рекуррентного соотношения, разработка которых является одним из методов решения задач.
Школьный курс математики содержит информацию о рекуррентных соотношениях в примерах арифметической и геометрической прогрессий.
В результате исследования учебников «Алгебра для 9 класса» авторов Ш.А Алимова, Ю.М Колягина, Ю.В Сидорова, Н.Е Федорова, М.И Шабунина, удалось отметить рекуррентные отношения в 5 главе в следующих параграфах:
— § 17 «Числовая последовательность»,
— § 18 «Арифметическая прогрессия»,
— § 20 «Геометрическая прогрессия».
Рассмотрим их более детально относительно рекуррентных соотношений.
Видео:Семинар №13 "Определители n го порядка"Скачать

2.1 Числовая последовательность
— числовая последовательность, в которой число — первый член последовательности, число — второй член последовательности, число — третий и т.д. Число называют -м(энным) членом последовательности, а натуральное число n — его номером.
Последовательность иногда задают формулой, которая позволяет вычислить -й член последовательности через предыдущие членов. В этом случае дополнительно задают один или несколько первых членов последовательности и такой способ задания последовательности называют рекуррентным (от латинского слова recurro -возвращаться). 8
Видео:10. Линейные однородные рекуррентные соотношения. Дискретная математикаСкачать

2.2 Арифметическая прогрессия
Рекуррентная последовательность второго порядка это и есть арифметическая прогрессия. При числовой последовательности а 1 ,а 2 ,а 3 ,….а n ,… ее можно считать арифметической прогрессией, тогда, когда для всех натуральных n выполняется равенство
Из этого следует, что
Число называют разностью арифметической прогрессии. 9
1) Натуральный ряд чисел 1,2,3,4,…, n ,… является арифметической прогрессией. Разность этой прогрессии .
2) Последовательность целых отрицательных чисел -1,-2,-3,…,- n ,-арифметическая прогрессия с разностью .
3) Последовательность 3,3,3,…,3,…-арифметическая прогрессия с разностью
Формула n -го члена арифметической прогрессии:
Сумма n первых членов арифметической прогрессии равна
Видео:ДМ 1 семестр 12 лекция: Подсчет КО и рекуррентные соотношенияСкачать

2.3 Геометрическая прогрессия
Рекуррентной последовательностью первого порядка называют геометрическую прогрессию. Числовая последовательность b 1 ,b 2 ,b 3 ,….b n ,…, если для всех натуральных n выполняется равенство:
– рекуррентная формула, где – некоторое число, не равное 0 – это и есть геометрическая прогрессия.
Сумма n первых членов геометрической прогрессии со знаменателем q 1 равна
Видео:рекуррентные соотношения 3Скачать

2.4 Практические задачи (из школьного курса математики)
Необходимо вычислить пятый член числовой последовательности.
При условии, что:
А) Числовая последовательность задана рекуррентной формулой
Выяснить, является ли последовательность — арифметической прогрессией?
Требуется доказать, что разность одна и та же для всех .
Запишем следующее: -й член данной последовательности:
Следовательно, разность не зависит от .
Исходя из определения арифметической прогрессии:
В итоге, каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов.
Необходимо найти сумму девяти первых членов арифметической прогрессии, если прогрессия задана условиями: , а 1 = 7.
a 9 = 7 – 3(9 – 1) = -17
Необходимо найти сумму первых пяти членов геометрической прогрессии, если ( b n ) задана следующими условиями: b 1 = – 7, b n +1 = – 3 b n .
В задаче требуется доказать, что последовательность, заданная формулой b n = , является геометрической прогрессией.
Отметим, что b n = при всех n .
Надо доказать, что частное – одно и тоже число для всех n .
Получаем, , т.е. частное не зависит от n .
В условии задачи даны n различных натуральных чисел, составляющих арифметическую прогрессию. Необходимо выяснить:
а) Может ли сумма всех данных чисел быть равной 14?
б) Каково наибольшее значение n , при условии, если сумма всех данных чисел меньше 900?
в) Найти все возможные значения n , если сумма всех данных чисел равна 123.
а) Да, может. Числа 2, 3, 4, 5 составляют арифметическую прогрессию, их сумма равна 14.
б) Возьмем a — первый член, d — разность, n — число членов прогрессии, тогда их сумма равна .
Для того, чтобы количество членов было наибольшим, первый член и разность должны быть наименьшими. Пусть они равны 1, тогда по условию Наибольшее натуральное решение этого неравенства n = 41. Такой результат получается при прогрессии 1+2+…+41=861
в) Для суммы членов арифметической прогрессии имеем:
Таким образом, число членов прогрессии n является делителем числа 246. Если то левая часть больше 246: , следовательно, n
Ответ: а) да; б) 41; в) 3; 6.
В условиях задачи последние члены двух конечных арифметических прогрессий a 1 = 5, a 2 = 8, . a N и b 1 = 9, b 2 = 14, . b M совпадают, а сумма всех совпадающих (взятых по одному разу) членов этих прогрессий равна 815. Найдите число членов в каждой прогрессии.
Общие члены прогрессий удовлетворяют уравнению:
Левая часть последнего уравнения делится на 3, поэтому то есть или где Найдём L .
Общие члены двух прогрессий сами образуют арифметическую прогрессию с первым членом равным 14, а последним — равным 15 L -1
Значит, откуда L =10.
Поэтому N =5 L -1=49, M =3 L -1=29
Необходимо вычислить пятый член последовательности, если числовая последовательность задана рекуррентной формулой и условиями .
Последовательность задана условием и рекуррентной формулой . Необходимо найти четыре последовательности.
В условиях задачи даны n различных натуральных чисел, составляющих арифметическую прогрессию . Необходимо определить:
а) Может ли сумма всех чисел быть равной 10?
б) Каково наибольшее значение n , если сумма всех данных чисел меньше 1000?
в) Найти все возможные значения n , если сумма всех данных чисел равна 129.
Целое число S является суммой не менее трех последовательных членов непостоянной арифметической прогрессии, состоящей из целых чисел. Необходимо определить следующее:
а) Может ли S равняться 8?
б) Может ли S равняться 1?
в) Найдите все значения, которые может принимать S.
В возрастающей последовательности натуральных чисел каждые три последовательных члена образуют прогрессию — арифметическую, либо геометрическую. Первый член последовательности равен 1, а последний 2076. Необходимо определить:
а) может ли в последовательности быть три члена?
б) может ли в последовательности быть четыре члена?
в) может ли в последовательности быть меньше 2076 членов?
Найдите все целые значения m и k такие, что
В условиях дана арифметическая прогрессия (с разностью, отлично от нуля), составленная из натуральных чисел, десятичная запись которых не содержит цифры 9. Необходимо:
а) Определить может ли в такой прогрессии быть десять членов?
б) Доказать, что число её членов меньше 100.
в) Доказать, что число членов всякой такой прогрессии не больше 72.
г) Привести пример такой прогрессии с 72 членами
Найти трехзначное число, которое делится на 45 и цифры которого образуют арифметическую прогрессию.
Найти пятый член бесконечно убывающей геометрической прогрессии, если известно, что ее сумма равно 9, а сумма квадратов ее членов равна 40,5.
В условиях задачи три числа составляют геометрическую прогрессию. Если от третьего числа вычесть 4, то числа составят арифметическую прогрессию. Если же от второго и третьего членов полученной арифметической прогрессии вычесть по 1, то снова получим геометрическую прогрессию. Необходимо найти эти числа.
При условии, что все члены геометрической прогрессии — различные натуральные числа, заключенные между числами 210 и 350 надо выяснить:
а) может ли такая прогрессия состоять из четырех членов?
б) может ли такая прогрессия состоять из пяти членов?
Бесконечная арифметическая прогрессия a 1 , a 2 , . a n , . состоит из различных натуральных чисел.
а) Существует ли такая прогрессия, в которой среди чисел a 1 , a 2 , . a 7 ровно три числа делятся на 100?
б) Существует ли такая прогрессия, в которой среди чисел a 1 , a 2 . a 49 ровно 11 чисел делятся на 100?
На доске написано 30 чисел: 10- «5», 10- «4» и 10 — «3». Эти числа разбивают на две группы, в каждой из которых есть хотя бы одно число.
Среднее арифметическое чисел в первой группе равно А , среднее арифметическое чисел во второй группе равно В . (Для группы из единственного числа среднее арифметическое равно этому числу.)
а) Приведите пример разделения исходных чисел на две группы, при котором среднее арифметическое всех чисел меньше
б) Докажите, что если разделить исходные числа на две группы по 15 чисел, то среднее арифметическое всех чисел будет равно
в) Найдите наибольшее возможное значение выражения
Последовательность а 1 , а 2 ,…,а 7 состоит из неотрицательных однозначных чисел. Возьмем условия, при которых пусть М 1 — среднее арифметическое всех членов этой последовательности, кроме k -го. Известно, что M 1 = 1, M 2 = 2.
а) приведите пример такой последовательности, для которой M 3 = 1,5.
б) существует ли такая последовательность, для которой M 3 = 3?
в) Найдите наибольшее значение M 3 .
Возрастающая конечная арифметическая прогрессия состоит из различных целых неотрицательных чисел. Математик вычислил разность между квадратом суммы всех членов прогрессии и суммой их квадратов и прибавил к этой прогрессии следующий её член, и снова вычислил такую же разность.
а) Приведите пример такой прогрессии, если во второй раз разность оказалась на 48 больше, чем в первый раз.
б) Во второй раз разность оказалась на 1440 больше, чем в первый раз. Могла ли прогрессия сначала состоять из 12 членов?
в) Во второй раз разность оказалась на 1440 больше, чем в первый раз. Какое наибольшее количество членов могло быть в прогрессии сначала?
Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 1512 и
в) три из них образуют геометрическую прогрессию?
Видео:Олегу Тинькову запрещён вход на Мехмат МГУСкачать

Заключение
В науке широкое использование получили рекуррентные числовые последовательности чисел Фибоначчи, Люка и др. Они же, как простейшие числовые последовательности, более всего исследованы. В последние годы на основе последовательности Фибоначчи были также исследованы обобщенные числовые последовательности. Последовательность Фибоначчи (q = р = 1) – простейшая рекуррентная последовательность, которая является линейной функцией с постоянными коэффициентами, что и было показано в процессе исследования.
В результате проведенного исследования были изучены методы решения рекуррентных соотношений: метод математической индукции, метод итерации(подстановки), метод производящих функций, методы решения однородных и неоднородных рекуррентных соотношений.
Были проанализированы действующие учебники математики, а также изучена учебно-методическая литература по данной теме. Подобраны задачи из школьного курса математики для демонстрации излагаемого теоретического материала.
Изучив использованные материалы, удалось установить, что преподаватель математики в пределах школьного курса знакомит учеников с
понятием и особенностями рекуррентных соотношений на примерах прогрессий – арифметической, геометрической. Если же брать изучение других видов, к примеру, числа Фибоначчи, то такой вид рекуррентных соотношений включается в программу факультативных занятий, в процессе которых школьники узнают методы их решения. Как правило, оно заключается в методе математической индукции, где требуется определенный навык построения правильного индуктивного предположения.
В результате проведенного исследования также выделим, что методы решения рекуррентных соотношений бывает очень прост, а периодически требует приложить серьезные усилия. Из-за чего в процессе решения одних задач рекуррентные соотношения бывают простые, а в другом случае — сложные. Но, в любом случае, объединяет все тот нюанс, что для вычисления члена последовательности всегда надо вычислить предшествующие члены.
Обобщая полученную информацию в процессе работы над курсовой, по результатам проведенного исследования стоит отметить:
— в действующих школьных учебниках теория данной тематики изложена недостаточно;
— в учебниках рассмотрены рекуррентные соотношения на ознакомительном уровне и среди предлагаемых заданий много однотипных;
— рассмотренные рекуррентные соотношения более детально изучаются углубленно на профильном уровне, на факультативных занятиях, на элективных курсах, нежели на стандартных уроках, включенных в школьную программу.
Задачи, поставленные перед началом работы были решены и цель курсовой работы успешно достигнута.
Дискретная математика — рекуррентное соотношение
В этой главе мы обсудим, как рекурсивные методы могут выводить последовательности и использоваться для решения задач подсчета. Процедура поиска членов последовательности рекурсивным способом называется рекуррентным отношением . Мы изучаем теорию линейных рекуррентных соотношений и их решения. Наконец, мы вводим производящие функции для решения рекуррентных отношений.
Определение
Рекуррентное отношение — это уравнение, которое рекурсивно определяет последовательность, в которой следующий член является функцией предыдущих членов (выражая F n как некоторую комбинацию F i с i n ).
Пример — ряд Фибоначчи — F n = F n − 1 + F n − 2 , Ханойская башня — F n = 2 F n − 1 + 1
Линейные рекуррентные отношения
Линейное рекуррентное уравнение степени k или порядка k — это рекуррентное уравнение в формате x n = A 1 x n − 1 + A 2 x n − 1 + A 3 x n − 1 + d o t s A k x n k ( A n — константа, а A k n e q 0 ) на последовательности чисел как полинома первой степени.
Вот некоторые примеры линейных рекуррентных уравнений —
| Рецидив отношений | Начальные значения | Решения |
|---|---|---|
| F n = F n-1 + F n-2 | a 1 = a 2 = 1 | Число Фибоначчи |
| F n = F n-1 + F n-2 | а 1 = 1, а 2 = 3 | Номер Лукаса |
| F n = F n-2 + F n-3 | a 1 = a 2 = a 3 = 1 | Падовская последовательность |
| F n = 2F n-1 + F n-2 | a 1 = 0, a 2 = 1 | Число Пелла |
Как решить линейное рекуррентное соотношение
Предположим, что два упорядоченных линейных рекуррентных соотношения имеют вид — F n = A F n − 1 + B F n − 2 , где A и B — действительные числа.
Характеристическое уравнение для вышеуказанного рекуррентного соотношения —
x 2 − A x e − B = 0
Три случая могут возникнуть при поиске корней —
Случай 1 — Если это уравнение учитывается как ( x − x 1 ) ( x − x 1 ) = 0 и оно дает два различных реальных корня x 1 и x 2 , то F n = a x n 1 + b x n 2 является решение. [Здесь a и b являются константами]
Случай 2 — Если это уравнение вычисляется как ( x − x 1 ) 2 = 0 , и оно порождает один действительный корень x 1 , то решением является F n = a x n 1 + b n x n 1 .
Случай 3 — Если уравнение дает два различных комплексных корня, x 1 и x 2 в полярной форме x 1 = r a n g l e t h e t a и x 2 = r a n g l e ( − t h e t a ) , то F n = r n ( a c o s ( n t h e t a ) + b s i n ( n t h e t a ) ) является решением.
Решите рекуррентное соотношение F n = 5 F n − 1 − 6 F n − 2 , где F 0 = 1 и F 1 = 4 .
Характеристическое уравнение рекуррентного соотношения —
Итак, ( x − 3 ) ( x − 2 ) = 0
x 1 = 3 и x 2 = 2
Корни реальны и различны. Итак, это в форме дела 1
F n = a x n 1 + b x n 2
Здесь F n = a 3 n + b 2 n ( A s x 1 = 3 a n d x 2 = 2 )
1 = F 0 = a 3 0 + b 2 0 = a + b
4 = F 1 = a 3 1 + b 2 1 = 3 a + 2 b
Решая эти два уравнения, мы получаем a = 2 и b = − 1
Следовательно, окончательное решение —
$$ F_n = 2,3 ^ n + (-1). 2 ^ n = 2,3 ^ n — 2 ^ n $$
Решите рекуррентное соотношение — F n = 10 F n − 1 − 25 F n − 2 , где F 0 = 3 и F 1 = 17 .
Характеристическое уравнение рекуррентного соотношения —
x 2 − 10 x − 25 = 0
Итак, ( x − 5 ) 2 = 0
Следовательно, существует один действительный корень x 1 = 5
Поскольку существует единый действительный корень, он имеет вид случая 2
F n = a x n 1 + b n x n 1
3 = F 0 = a .5 0 + b .0 .5 0 = a
17 = F 1 = a .5 1 + b .1 .5 1 = 5 a + 5 b
Решая эти два уравнения, мы получаем a = 3 и b = 2 / 5
Следовательно, окончательное решение — F n = 3.5 n + ( 2 / 5 ) . n .2 n
Решите рекуррентное соотношение F n = 2 F n − 1 − 2 F n − 2 , где F 0 = 1 и F 1 = 3
Характеристическое уравнение рекуррентного соотношения —

