Рекуррентная система уравнений и способ ее решения (5 видео)

Рекуррентные соотношения и уравнения

В этом разделе вы найдете бесплатные примеры решений рекуррентных соотношений методом характеристического уравнения и подбора частного решения по правой части. Также приведены краткие алгоритмы решения для двух методов и пример их использования для последовательности Фибоначчи.

Содержание

Как решать рекуррентные соотношения?
Метод производящих функций
Метод характеристических функций
Решение для последовательности чисел Фибоначчи
Способ 1. Производящяя функция
Способ 2. Характеристическое уравнение
Примеры решений
Применение многочленов от матриц для решения систем рекуррентных уравнений
Алгоритм решения системы рекуррентных уравнений
Дискретная математика — рекуррентное соотношение
Определение
Линейные рекуррентные отношения
Как решить линейное рекуррентное соотношение
🎥 Видео

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Как решать рекуррентные соотношения?

Для решения рекуррентных соотношений применяют один из двух основных способов:

Метод производящих функций
Метод характеристического уравнения

В следующем разделе мы сравним, как выглядит процесс решения для одной и той же последовательности двумя методами.

Метод производящих функций

Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен $k$) $$a_ = …, \ a_ = …, \ a_ = …, \ … \ a_ = …, ngeqslant k$$
Домножить каждую строчку на $z$ в соответствующей степени $z^ cdot a_$ и сложить все выражения для $n ge 0$. В левой части получится сумма $displaystylesum_^ a_nz^n$ — это производящая функция, назовем ее $G(z)$. Правую часть преобразовать так, чтобы она превратилась в выражение, включающее $G(z)$.
Решить полученное уравнение относительно $G(z)$.
Разложить $G(z)$ в степенной ряд, тогда коэффициент при $z_n$ будет искомым выражением для $a_n$.

Метод характеристических функций

Этот метод практически полностью аналогичен методу решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, кратко алгоритм выглядит так:

Записать соответствующее однородное рекуррентное уравнение (РУ): $$ p_ a_ + p_a_ + . + p_n a_n =f to \ to p_ a_ + p_a_ + . + p_n a_n =0. $$
Выписать для него характеристическое уравнение и найти его корни $lambda_i$ $$ p_ lambda^ + p_lambda^ + . + p_lambda + p_n =0. $$
Выписать согласно полученным корням $lambda_1, . lambda_k$ общее решение однородного рекуррентного соотношения (подробнее теорию см. по ссылке [1] ниже). $$ C_1 lambda_1^n +. +C_k lambda_k^n , mbox , $$ $$ C_1 lambda_1^n + C_2 nlambda_1^n +. +C_m n^m lambda_1^n+. +C_k lambda_k^n mbox , lambda_1 , , m. $$
Подобрать частное решение неоднородного рекуррентного соотношения по виду правой части (особенно удобно для правых частей вида $mu^n*P(n)$, $P(n)$ — многочлен от $n$).
Представить общее решение неоднородного РУ как сумму общего решения соответствующего однородного РУ и частного решения неоднородного РУ.
Подставить начальные условия $a_0, a_1, . a_$ и получить значения констант $C_1, . C_k$.

Видео:Решение рекуррентных уравненийСкачать

Решение для последовательности чисел Фибоначчи

Последовательность чисел Фибоначи — это последовательность, каждый элемент которой (кроме нулевого и первого) равен сумме двух предыдущих:

$$ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 , . $$

Числа Фибоначчи растут быстро: $f_=55$, $f_=6765$, а $f_=354224848179261915075$.

Общая формула данной рекуррентной последовательности имеет вид6

Способ 1. Производящяя функция

Начинаем с второго шага алгоритма, домножаем на $z^n$:

$$begin 1cdot f_0 &= &0cdot 1,\ zcdot f_1 &= &1cdot z,\ zcdot f_n & = &(f_+f_)cdot z^n, quad ngeq2.\ end $$

Складываем все строчки:

На третьем шаге алгоритма приводим все суммы к замкнутому виду:

откуда выводим искомое выражение для производящей функции:

Теперь разложим ее в степенной ряд. Для этого сначала разложим знаменатель на множители. Найдем корни уравнения:

Чтобы разложить данные дроби в ряды, используем известное разложение для дроби:

Рассмотрим первую дробь и поделим в ней числитель и знаменатель на $z_1$:

Аналогично (но с делением на $z_2$) действуем со второй дробью:

Преобразуем данное выражение, используя то, что

$$1/z_1=-z_2, quad 1/z_2 = -z_1, quad z_1-z_2=sqrt $$ $$f_n=frac<sqrt>left( biggl( frac<1+sqrt> biggr)^n — biggl( frac<1-sqrt> biggr)^n right). $$

Способ 2. Характеристическое уравнение

Запишем характеристический многочлен для $f_n=f_+f_$, и найдем его корни:

Тогда общее решение однородного рекуррентного уравнения имеет вид:

Осталось найти значения произвольных постоянных $C_1, C_2$ из начальных условий $f_0=0, f_1=1$.

Решая систему, найдем

Итоговое выражение для последовательности чисел Фибоначчи:

Результаты обоих методов совпали, решение вторым методом оказалось проще и короче.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Примеры решений

Задача 1. Решить рекуррентное соотношение $f(n+2)=-6f(n+1)+7f(n)+n-3$ с начальными условиями $f(0)=2$ и $f(1)=4$, сделать проверку

Задача 2. Решить рекуррентное соотношение $f(n+2)=-2f(n+1)+3f(n)-3^n$ с начальными условиями $f(0)=1$, $f(1)=3$ и сделать проверку

Задача 3. 1. Решить рекуррентное соотношение $f(n+2) =-5f(n+1) -4f(n) + 3n^2$ с начальными условиями $f(0) = 2$, $f(1) = 3$.
2. Проверить, удовлетворяет ли найденное решение начальным условиям и обращает ли оно рекуррентное соотношение в справедливое тождество.

Задача 4. Найти последовательность $$, удовлетворяющую рекуррентному соотношению $a_ + 4 a_ + 3 a_ = 0$ и начальным условиям $a_1=2$, $a_2=4$.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Применение многочленов от матриц для решения систем рекуррентных уравнений

Рассмотрим систему линейных рекуррентных уравнений

где — коэффициенты системы , — заданные, а — неизвестные функции дискретного аргумента , . При описании дискретных динамических систем аргумент в (7.47) называют дискретным временем .

Систему (7.47) можно записать в матричном виде:

где — квадратная матрица (n-го порядка) коэффициентов системы рекуррентных уравнений, — столбец заданных функций, a — столбец неизвестных.

Решением системы (7.48) называется последовательность столбцов , при подстановке которых в (7.48) получаются верные равенства для всех .

Поставим задачу нахождения решения системы (7.48), удовлетворяющего начальным условиям

где — заданный столбец.

Рассмотрим сначала однородную систему с постоянными коэффициентами

Записывая (7.50) для , последовательно получаем

Следовательно, решение однородной системы (7.50), удовлетворяющее начальным условиям (7.49), имеет вид:

Получим теперь решение системы (7.48). Учитывая (7.49), запишем (7.48) для

и т.д. Следовательно, решение системы (7.48) имеет вид

Первое слагаемое в (7.52) — решение однородной системы (7.50) с начальными условиями (7.49), второе слагаемое — решение системы (7.48) с нулевыми начальными условиями (т.е. при ).

Видео:21.04 - дискра, рекуррентные соотношенияСкачать

Алгоритм решения системы рекуррентных уравнений

Для нахождения решения системы (7.48) с начальными условиями (7.49) требуется выполнить следующие действия.

1. Найти выражение для степени матрицы одним из способов, рассмотренных ранее.

2. Записать по формуле (7.52) искомое решение.

1. Линейное рекуррентное уравнение с постоянными коэффициентами:

может быть сведено к эквивалентной системе рекуррентных уравнений вида (7.47). Действительно, используя обозначения

или в матричной форме (7.48): с матрицами и

Пример 7.19. Найти решение рекуррентного уравнения с начальными условиями

Решение. В соответствии с пункту 1 замечаний 7.11 составим систему уравнений

где . Требуется найти решение этой системы, удовлетворяющее начальным условиям: .

1. Составим матрицу системы и найдем ее степень , используя второй способ. Характеристический многочлен имеет вторую степень и два простых корня: . Поэтому многочлен (7.44) — линейный: . Для его коэффициентов записываем систему (7.46):

Отсюда . Таким образом,

2. По формуле (7.52) записываем решение системы (учитывая, что ):

Нас интересует только первый элемент этого столбца:

Решение совпадает с найденным в примере 2.15.

Пример 7.20. Найти решение системы рекуррентных уравнений с начальными условиями

Решение. Запишем систему в матричной форме (7.48) и начальные условия

1. Выражение для степени матрицы найдено в примерах 7.17 и 7.18:

2. Выражение, полученное для , справедливо только при 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC8AAAAQCAMAAACx1dbmAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAiXFYMbEhAcBBoPDQoeAQ0I3cqgAAALZJREFUKM+VktsSwyAIRDWKiFf+/2uLSZvEhkxaXnTGs7KsGvN3UYrwC+ffa3D8zCMlxo+QlyfcNmg7v7A/t7VBux/jzkOe54lJURw8ZrHvop0UdM8P+3axGc89aqQ7XuxbjzybMkEUqPLAIPP6/u0g1OYUHnMpTQs02KLxq/0p0Y1O0al+RvqOCcv51CeZF1UeJBjhacoT6PJehTd9k/R7gdgPul7ei3itcWeYPp/sqv4fRhnzAuOaBpbDogV3AAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> (см. пример 7.18). Поэтому для формулу (7.52) нельзя использовать. Найдем непосредственно из системы (7.53)

Далее записываем искомое решение для , выделяя в формуле (7.52) слагаемые с и

В последней сумме слагаемые не зависят от индекса суммирования, т.е. это сумма одинаковых слагаемых. Поэтому, приводя подобные члены, получаем

Таким образом, решением заданной системы является последовательность столбцов:

Видео:Решение систем уравнений методом подстановкиСкачать

Дискретная математика — рекуррентное соотношение

В этой главе мы обсудим, как рекурсивные методы могут выводить последовательности и использоваться для решения задач подсчета. Процедура поиска членов последовательности рекурсивным способом называется рекуррентным отношением . Мы изучаем теорию линейных рекуррентных соотношений и их решения. Наконец, мы вводим производящие функции для решения рекуррентных отношений.

Видео:Метод Гаусса решения систем линейных уравненийСкачать

Определение

Рекуррентное отношение — это уравнение, которое рекурсивно определяет последовательность, в которой следующий член является функцией предыдущих членов (выражая F n как некоторую комбинацию F i с i n ).

Пример — ряд Фибоначчи — F n = F n − 1 + F n − 2 , Ханойская башня — F n = 2 F n − 1 + 1

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

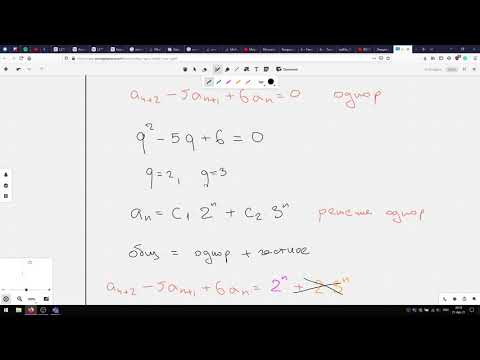
Линейные рекуррентные отношения

Линейное рекуррентное уравнение степени k или порядка k — это рекуррентное уравнение в формате x n = A 1 x n − 1 + A 2 x n − 1 + A 3 x n − 1 + d o t s A k x n k ( A n — константа, а A k n e q 0 ) на последовательности чисел как полинома первой степени.

Вот некоторые примеры линейных рекуррентных уравнений —

Рецидив отношений	Начальные значения	Решения
F _n = F _n-1 + F _n-2	a ₁ = a ₂ = 1	Число Фибоначчи
F _n = F _n-1 + F _n-2	а ₁ = 1, а ₂ = 3	Номер Лукаса
F _n = F _n-2 + F _n-3	a ₁ = a ₂ = a ₃ = 1	Падовская последовательность
F _n = 2F _n-1 + F _n-2	a ₁ = 0, a ₂ = 1	Число Пелла

Как решить линейное рекуррентное соотношение

Предположим, что два упорядоченных линейных рекуррентных соотношения имеют вид — F n = A F n − 1 + B F n − 2 , где A и B — действительные числа.

Характеристическое уравнение для вышеуказанного рекуррентного соотношения —

x 2 − A x e − B = 0

Три случая могут возникнуть при поиске корней —

Случай 1 — Если это уравнение учитывается как ( x − x 1 ) ( x − x 1 ) = 0 и оно дает два различных реальных корня x 1 и x 2 , то F n = a x n 1 + b x n 2 является решение. [Здесь a и b являются константами]

Случай 2 — Если это уравнение вычисляется как ( x − x 1 ) 2 = 0 , и оно порождает один действительный корень x 1 , то решением является F n = a x n 1 + b n x n 1 .

Случай 3 — Если уравнение дает два различных комплексных корня, x 1 и x 2 в полярной форме x 1 = r a n g l e t h e t a и x 2 = r a n g l e ( − t h e t a ) , то F n = r n ( a c o s ( n t h e t a ) + b s i n ( n t h e t a ) ) является решением.

Решите рекуррентное соотношение F n = 5 F n − 1 − 6 F n − 2 , где F 0 = 1 и F 1 = 4 .

Характеристическое уравнение рекуррентного соотношения —

Итак, ( x − 3 ) ( x − 2 ) = 0

x 1 = 3 и x 2 = 2

Корни реальны и различны. Итак, это в форме дела 1

F n = a x n 1 + b x n 2

Здесь F n = a 3 n + b 2 n ( A s x 1 = 3 a n d x 2 = 2 )

1 = F 0 = a 3 0 + b 2 0 = a + b

4 = F 1 = a 3 1 + b 2 1 = 3 a + 2 b

Решая эти два уравнения, мы получаем a = 2 и b = − 1

Следовательно, окончательное решение —

$$ F_n = 2,3 ^ n + (-1). 2 ^ n = 2,3 ^ n — 2 ^ n $$