Реконструкция обыкновенных дифференциальных уравнений по временным рядам (4 видео)

Безручко Б.П., Смирнов Д.А. Реконструкция обыкновенных дифференциальных уравнений по временным рядам

Учебно-методическое пособие, – Саратов: Издательст-во ГосУНЦ Колледж, 2000 – 46 с.

Рассматриваются подходы к построению динамических моделей с непрерывным временем по временным рядам. Демонстрируются методы глобальной реконструкции обыкновенных дифференциальных уравнений по векторным и скалярным рядам. Описываются приемы уменьшения влияния шумов. В практической части предлагается, пользуясь готовыми программами, получить временные реализации хаотических колебаний эталонных систем дифференциальных уравнений, реконструировать по ним модельные уравнения и оценить качество реконструкции.

Работы предназначены для практических занятий по курсу «Математическое моделирование».

Содержание
1. Введение
1.1. Дифференциальные уравнения и моделирование
с позиций детерминизма
1.2. Временные ряды
1.3. Конструирование, реконструкция, восстановление
2. Реконструкция дифференциальных уравнений по временному ряду
2.1. Общая схема реконструкции математической модели по временному ряду
2.2. Основные элементы процедуры для дифференциальных уравнений, стандартный подход
2.3. Критерии эффективности модели
3. Реконструкция уравнений по векторному ряду (работа № 1)
3.1. Процедура получения временного ряда производных, борьба с шумами
3.2. Практическое задание
3.3. Контрольные вопросы
4. Реконструкция уравнений по скалярному ряду (работа № 2)
4.1. Метод Брумхеда-Кинга
4.2. Вычисление нескольких производных наблюдаемой
4.3. Практическое задание
4.4. Контрольные вопросы
Приложение
1. Описание программы FlowSimulator
Приложение
2. Описание программы VectorODE
Приложение
3. Описание программы ScalarODE
Литература

Содержание

Реконструкция обыкновенных дифференциальных уравнений по временным рядам
Обзор моделей прогнозирования временных рядов: проба пера
Comments 33
🌟 Видео

Видео:Размышляю над Хаосом и Равновесием - ДиффурыСкачать

Реконструкция обыкновенных дифференциальных уравнений по временным рядам

Булдакова Т.И., Суятинов С.И.

Россия, Саратов, СГТУ

РЕКОНСТРУКЦИЯ ДИНАМИЧЕСКИХ СИСТЕМ НА НЕЙРОННЫХ СЕТЯХ

Рассмотрена задача моделирования методом реконструкции динамических систем по временным рядам. Отмечены недостатки существующих подходов. Показана возможность и преимущества решения подобной задачи на нейронных сетях. Особенности подхода исследованы на примере реконструкции системы по пульсограммам. Приведены результаты экспериментов на сети Хопфилда.

Многие проблемы управления, прогнозирования, распознавания образов связаны с задачей разработки математических моделей. Можно выделить два подхода к ее решению. Первый подход заключается в разработке модели, исходя из известных физических принципов и законов функционирования моделируемой системы. При втором подходе модель строят по временной реализации некоторой переменной состояния системы. В этом случае предполагается, что математическая модель представляет собой систему обыкновенных дифференциальных уравнений, приближенно описывающую эволюцию переменных состояния системы. Построение модели, или реконструкция динамической системы (ДС), собственно состоит в восстановлении модельных уравнений анализируемой системы, которые с заданной точностью способны воспроизводить экспериментально полученный временной ряд.

Остановимся более подробно на втором подходе, который наиболее применим к исследованию сложных систем, доступных для изучения только по своим реализациям. Наиболее ярким примером здесь являются медико-биологические системы, где достижения теории динамических систем могут находить свое практическое применение. В качестве примера рассмотрим задачу реконструкции динамической системы с целью диагностики и прогнозирования патологий по пульсограммам. Так, имея пульсовый сигнал (пульсограмму) и решая задачу реконструкции, можно оценить состояние здоровья человека, выявить патологии.

В данном случае интерес к пульсограммам обусловлен тремя причинами:

пульсовый сигнал является достаточно сложным по форме и обладает некоторыми особенностями, которые выделяют его из реализаций других колебательных систем, демонстрирующих хаотическое поведение;
данный сигнал легко доступен и позволяет эффективно проводить диагностику;
метод диагностики по пульсограммам системы имеет тысячелетнюю историю, его эффективность проверена веками.

Существующие методы обработки пульсограмм основаны на определении характерных точек, изгибов, величин пиков, спектральном анализе. Однако мозг человека плохо приспособлен для выполнения арифметических операций. Мозг создает на своих нейронных сетях образы и оперирует ими. С достоверностью можно предположить, что, ощущая пальцами пульс, тибетские медики реконструировали в мозгу динамическую модель составляющей человеческого организма.

Следует отметить, что наблюдаемые временные реализации представляют такие установившиеся режимы, которые достигаются в пределе при t ® ? . Это подразумевает наличие в фазовом пространстве системы притягивающего предельного множества точек — аттрактора. Поэтому задача реконструкции подразумевает задание подходящего фазового пространства и формирование предельных множеств, соответствующих исходной временной реализации. Этой задаче посвящено достаточно большое количество публикаций (например, [ 1 ] и библиография в ней).

Изложенные в [ 1 ] подходы к проблеме реконструкции ДС характеризуются следующими основными недостатками:

выбор полиномиальной нелинейности не всегда оправдан
результирующие уравнения получаются негрубыми, то есть малое изменение их параметров приводит к уходу фазовой траектории в бесконечность;
небольшое зашумление экспериментальных данных может существенно исказить результаты.

Нейронные сети являются более гибким аппаратом моделирования [2]. Аппроксимация нелинейностей осуществляется нейронными сетями. Каждый нейрон сети реализует простую нелинейную функцию одного аргумента j ( y). Нейрон имеет несколько входов, на которые поступает вектор сигналов X. Значимость входов одного нейрона определяется вектором весов w. Для сети из n нейронов, на входы которых подается вектор сигналов X, будем иметь n векторов w, которые образуют матрицу весовых связей W.

Аргументом нелинейной функции нейрона является скалярное произведение (X,W), т.е. j (y) = j [(X,W)]. Здесь j — это сигмоидная функция активации нейрона, j = 1 ¤ ( 1 + e -y ) . Результат преобразований передается на входы других нейронов. Нелинейное преобразование исходного образа X=<x₁,x₂,…,x_n> происходит по правилу

Нейронная сеть представляет суперпозиции простых функций одной переменной и их линейные комбинации и производит аппроксимации нелинейных функций [ 3 ] . Так же, как и в случае с полиномами, матрица W ищется исходя из условия минимизации ошибки аппроксимации. Главное отличие заключается в том, что структура матрицы W (симметрия и знаки элементов) задается первоначально произвольно. На последующих шагах аппроксимации значения элементов определяются, например, методом наименьших квадратов. Избыточность информации в сетевых связях обеспечивает грубость аппроксимации при высокой точности.

Помимо аппроксимации нелинейностей нейронные сети являются универсальным средством представления оператора эволюции. В этом случае правила преобразования образа (1) заменяются системой нелинейных дифференциальных уравнений нейронной динамики

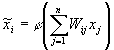
Здесь V_i(t) — состояние i — го нейрона в момент времени t; b_i -усиление; матрица W_ij и функция j имеют тот же смысл, что и раньше. В зависимости от выбора коэффициентов b_i, c_i получаются сети разных типов.

Для динамических систем подобного типа теорема Коэна-Гроссберга гарантирует существование областей притяжения — аттракторов. Эти области формируются в процессе синтеза матрицы W на основе исходных или эталонных образов. Эволюция состояния реконструированной нейронной сети приводит ее в область или точку равновесия. Эта область характеризуется локальным минимумом энергии, координаты которого соответствуют эталонному образу.

Из уравнения (2) можно получить следующее

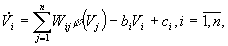
где b_i — коэффициенты обратной связи, c_i — внешнее воздействие на i — й нейрон. Полученное уравнение описывает сеть Хопфилда. Эта сеть выбрана для реконструкции динамической системы по данным пульсограмм.

Сети Хопфилда используются для запоминания статических образов, которые представляют точки аттракторов в фазовом пространстве нейронной системы.

Временные реализации реконструируемых систем представляют предельные множества другого типа. В простейшем случае — это предельный цикл. Возможны также более сложные образования. Поэтому особенность реконструкции на сетях Хопфилда заключается в формировании не точки равновесия, а предельного цикла. Эта особенность налагает дополнительные условия на правила синтеза матрицы W [4]. В частности, в экспериментальных исследованиях матрица была выбрана несимметричной. Помимо этого, структура сети учитывала то, что исходный сигнал является почти периодическим. Количество нейронов определялось из выражения n = (T/ t )+1, где T — период исходной реализации, t — дискретность съема информации.

Были проведены две серии экспериментов. Первая серия экспериментов базировалась на теореме Такенса [ 5 ] . В качестве эталонных образов выбирались исходная реализация вида

и ее модификации, полученные простой перенумеровкой a_i = a_i+1. Таким образом, сети было представлено n эталонов.

Вторая серия экспериментов основывалась на последовательном дифференцировании исходной временной последовательности. В качестве фазовых переменных использовались значения a(t), a'(t) и a»(t). Поэтому сеть содержала 3n элементов. Выбор трехмерного пространства обусловлен тем, что оценка размерности Хаусдорфа оказалась равна 2,75.

Экспериментально доказана возможность реконструкции ДС на нейронных сетях в обеих сериях экспериментов. Решения реконструированных уравнений модели качественно повторяют основные особенности исходного сигнала, однако сходство в деталях проявляются не всегда. Кроме того, предельные циклы возникали только при определенных численных значениях исходных реализаций. Отметим, что вторая серия экспериментов менее чувствительна к числам.

Дальнейшие исследования необходимо направить на совершенствование методики определения матрицы связи и структуры сети, которые гарантированно приводили к предельным циклам.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Обзор моделей прогнозирования временных рядов: проба пера

Видео:В.В. Власов. Корректная разрешимость и представление решений интегро-дифференциальных уравнений...Скачать

Comments 33

Существует еще один довольно мощный метод, основанный на нелинейной динамике. Это метод реконструкции исходных уравнений процесса. Суть его в том, что вы из одномерного ряда получаете многомерный а далее на его основе восстанавливаете уравнения системы (точнее их приближение) в аналитическом виде

Как он называется?

Кроме этого существует так же метод SSA

Сорри, вот ссылка ru.wikipedia.org/wiki/SSA_(метод)
Вот пример с прогнозированием SSA

«Как он называется?»

Он так и называется «Реконструкция обыкновенных дифференциальных уравнений по временным рядам»

За ссылку спасибо, открыла, выглядит солидно!

Не, модели на каких-либо диффурах я как-то не отношу к стохастическим моделям. Вероятно, это ближе к детерминированным моделям.

Моделей много всяких разных. Спасибо за пояснение! Хочется прежде со стохастическими разобраться, а потом уж пошире смотреть.

Вы сам этим занимались? Или просто про это слышали?

Он так и называется «Реконструкция обыкновенных дифференциальных уравнений по временным рядам»

Это более-менее общеизвестная общая идея, а не название метода. Это примерно как на вопрос о некоем методе оптимизации сказать «Он так и называется — ‘Минимизация функции n аргументов’».

Использование нейронных сетей — это даже меньше, чем идея, это — отсутствие идей 🙂

А если серьезно, то использование нейронных сетей — это действительно не метод. Метод — это, например, «использование двухслойного перцептрона» (да, я знаю, что он почти никогда не работает на практике).

каких-то общепринятых алгоритмов в этой сфере пока нет — она динамично развивается

А что, разве есть хоть какие-то, пусть и необщепринятые? Про «метод задержек» и «размерность пространства вложения» (а на самом деле — инерциального многообразия) — это все уже навязло в зубах у всех. А вот полноценная реконструкция динамической системы по временному ряду — тут я вообще ни одной разумной работы не видел. Ваша ссылка очень хорошая (как все учебные книжки Лоскутова), но там тоже про это почти ничего нет. К тому же это учебник, содержащий более-менее общеизвестные вещи. Собственно, я даже в целом понимаю, почему это ни у кого не получается, но вдруг Вы видели что-то интересное в этой области.

Дело в том, что хороший обзор мне найти не удалось: они или узкие, или специализированные.

Узкие. То есть откровенная халтура, как на английском, так и на русском, где перечисляется от силы половина указанного списка. И все, на этом автор начинает двигаться дальше.

Специализированные. Вот это встречается чаще. Если человек прогнозирует, например, временной ряд энергопотребления, то он делает обзор моделей, на которых именно такого рода ряд прогнозируется. В связи с этим снова выходит усечение.

Наверное, самый приличный обзор методов + оценка их достоинств и недостатков на русском — в моей диссертации: Обзор моделей прогнозирования и Сравнение моделей прогнозирования.

Из обзоров, к сожалению, порекомендовать больше нечего.

В дальнейшем, коли у меня руки дойдут, то я бы хотела описать все перечисленные модели с примерами реализации. Кое-что я уже сделала для своего сайта, кое-что еще только предстоит делать. Мне здесь бы просто хотелось получить ссылки полезные, если кто-то нашел, видел, использует модели. Разбираться мне приходится много, но найти из кучи материала то, что действительно просто и полезно, непросто и очень трудоемко.