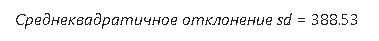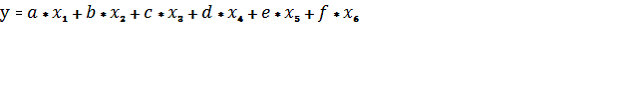Регрессионные модели рынка уравнения регрессии

Модели регрессии в бизнесе — Бизнес

Видео:Множественная регрессия в ExcelСкачать

Содержание:

• Модель регрессии: определение
• Модель регрессии: использование
• Модель регрессии: цель
• Стратегии регрессионного моделирования для обеспечения точности
• Модель регрессии: пример
• Модель регрессии: типы
• Преимущества регрессионного анализа
• Ограничения регрессионного анализа
• Корреляция против причинно-следственной связи

Рецензент: Джейн Томпсон, бакалавр права, магистр права

Как руководитель малого бизнеса, никто не несет большей ответственности за направление и успех вашего бизнеса, чем вы. Ваша команда может быть полезной, но в конечном итоге решения о направлении и стратегии, скорее всего, ложатся на ваши плечи.Наличие данных и полной информации важно для успешного принятия решений, и хорошая регрессионная модель может помочь вам спрогнозировать будущие тенденции для создания эффективных стратегий.

Эти инструменты прогнозирования помогут вам изучить взаимосвязь между переменными, которые влияют на ваш бизнес, такими как экономические тенденции, тенденции продаж, удовлетворенность сотрудников, удовлетворенность клиентов и многое другое.

Видео:Эконометрика. Линейная парная регрессияСкачать

Модель регрессии: определение

Если вы когда-нибудь задумывались, как компании предсказывают загруженное, медленное время, прибыль, убытки и другие переменные, то изучение определения прогнозирования с помощью регрессионной модели, вероятно, ответит на некоторые из ваших вопросов. Модель регрессии показывает взаимосвязь между двумя разными типами переменных:

Независимые переменные: Эти переменные не зависят от других переменных.

Например, регрессионная модель может показать корреляцию между независимой переменной валового внутреннего продукта или ВВП и зависимой переменной темпов продаж. Когда вы понимаете корреляцию между различными переменными, вы можете лучше прогнозировать будущие тенденции, оптимизировать операции и планировать взлеты и падения своего бизнес-цикла.

Видео:Множественная регрессияСкачать

Модель регрессии: использование

Модели регрессии используются для ответа на ваши вопросы о вашем бизнесе, чтобы вы могли решать проблемы заранее, а не реагировать. Вот некоторые из вопросов, на которые вы можете ответить с помощью регрессионной модели:

Как продажи соотносятся с колебаниями ВВП?

Как машинное производство влияет на срок хранения?

Чем отличается удовлетворенность клиентов, когда одежда шьется вручную?

Как время ожидания обслуживания клиентов влияет на удержание клиентов?

Как мы можем составить бюджет на случай прогнозируемой рецессии?

Модели регрессии могут использоваться для ответа на любые ваши вопросы о вашем бизнесе, которые включают независимые и фиксированные переменные. Они могут помочь вам понять взаимосвязь между этими переменными, чтобы вы могли прогнозировать будущие тенденции и оптимизировать операции соответственно. Например, если ваша регрессионная модель коррелирует продажи с колебаниями ВВП, вы можете использовать ее как для прогнозирования будущих продаж, так и для оптимизации производства, чтобы минимизировать потери.

Видео:РЕГРЕССИОННЫЙ АНАЛИЗ общая идея | АНАЛИЗ ДАННЫХ #16Скачать

Модель регрессии: цель

Цель регрессионной модели — помочь вам выяснить какие переменные влияют на ваш бизнес больше всего и насколько тесно они коррелируют. Ваше чутье может сказать вам, что на продажи в следующем месяце могут повлиять самые разные факторы. Некоторые из этих переменных могут включать:

• Погода
• ВВП
• Акции конкурентов
• каникулы
• Планируемые продажи
• Изменения в продукте
• Маркетинг
• Культурные тенденции

Модели регрессии помогают выйти за рамки этого подавляющего множества переменных, чтобы выяснить, что действительно больше всего влияет на ваш бизнес. Вы можете подумать, что ВВП больше всего влияет на продажи, в то время как ваш помощник менеджера убежден, что погода является движущим фактором. Модель регрессии может помочь вам увидеть, какая из этих двух переменных на самом деле больше всего коррелирует с колебаниями продаж.

Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Стратегии регрессионного моделирования для обеспечения точности

Стратегии регрессионного моделирования зависят от сбора точные данные представляющие независимые и зависимые переменные, которые вы пытаетесь исследовать. Ваша регрессионная модель точна ровно настолько, насколько точны компилируемые вами данные, поэтому необходимо тщательно следить за тем, чтобы вы включили в нее каждый бит информации, которую можете найти. Например, если вы хотите знать, как дождливые дни влияют на продажи, вы можете собирать итоговые данные о количестве осадков и продажах за каждый день за последние четыре года. Это может быть относительно просто, если у вас есть только одно местоположение магазина, но если у вас есть три местоположения, данные необходимо будет собирать и анализировать для каждого местоположения отдельно.

Чем сложнее ваша регрессионная модель, тем больше вероятность того, что при сборе данных у вас будут ошибки, которые могут кардинально изменить внешний вид вашего прогноза. Некоторые стратегии регрессионного моделирования, помогающие повысить точность данных, включают:

Собирайте одни и те же данные из более чем одного источника.

Попросите более одного человека собрать и обобщить данные.

Сравните данные и модели регрессии, составленные разными сторонами.

Дважды или трижды проверьте свои числа, прежде чем наносить их на регрессионную модель.

Используйте компьютерные программы, предназначенные для предупреждения вас о возможных неточностях в данных.

При обнаружении ошибок и несоответствий в данных вы можете пропустить данные, изменить данные или принять данные, если несоответствие статистически незначимо. Прежде чем включать неправильные данные, убедитесь, что они действительно является статистически незначимо. Часто лучше пропустить данные за один день, чем включить то, что, как вы знаете, неточно.

Видео:Парная регрессия: линейная зависимостьСкачать

Модель регрессии: пример

Один из примеров регрессионной модели может показать, насколько тесно связаны между собой температура выше 90 градусов и продажи снежных шишек в июле. Для создания этой регрессионной модели вам потребуются следующие данные:

Ежедневные температуры в июле за последние несколько лет

Чтобы создать пример регрессионной модели из этих данных, вы должны начать с точечного графика, называемого диаграмма рассеяния, где по оси Y отложены продажи снежных шишек (ваша зависимая переменная), а по оси X отложена температура (ваша независимая переменная).

Каждая точка, которую вы помещаете на графике, представляет собой количество продаж и температуру. Если эти два значения тесно коррелируют, линия, проходящая через середину всех точек данных, должна показывать восходящий тренд и поможет вам предсказать, сколько вы продадите при повышении температуры. Эта линия называется линия регрессии и можете сообщить, как вы планируете расходные материалы, укомплектование персоналом, специальные предложения и многое другое.

Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Модель регрессии: типы

Существует более 30 типов регрессионных моделей, но не все из них часто используются в бизнес-среде. Каждый тип регрессионной модели имеет свои собственные уравнения, и линейная регрессия Модель, например, снежный конус, очень популярна в бизнесе. Различные формы этой модели учитывают разное количество независимых и зависимых переменных. Это наиболее целесообразно, когда линия, проведенная через точки на точечной диаграмме, по природе прямая.

Некоторые другие типы регрессионных моделей включают:

• Логистическая регрессия
• Полиномиальная регрессия
• Регрессия хребта
• Регрессия лассо
• Регрессия ElasticNet

Отслеживание сложных уравнений, необходимых для каждого типа регрессионной модели, может показаться сложным для среднего специалиста в области малого бизнеса, не имеющего обширной подготовки в области статистики. К счастью, программное обеспечение для статистического анализа предназначен для выполнения математических расчетов за вас, если вы можете поддерживать точные базы данных, которые помогают создавать различные регрессионные модели, актуальные для вашего бизнеса, без необходимости запоминать список уравнений. Некоторые варианты программного обеспечения для статистического анализа, которые включают возможности регрессионного анализа, включают:

NLREG: Предлагает возможности модели линейной и нелинейной регрессии.

Анализируй-это: Работает в Excel для обеспечения множественной регрессии и другого статистического анализа.

Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Преимущества регрессионного анализа

Большинство малых предприятий на регулярной основе производят большие объемы неорганизованных данных, которые могут быть полезны при правильной интерпретации. Подумайте о том, как регрессия может дать вам возможность использовать данные о продажах, вашей рабочей силе, выпуске новых продуктов, налогах и многом другом для развития вашего бизнеса. Разумное использование приложений регрессионной модели может дать некоторые из следующих пяти преимуществ:

Идентификация ошибки: Что, если вы думаете, что ВВП наиболее тесно коррелирует с продажами, когда на самом деле погода или запуск новых продуктов?

Повышенная операционная эффективность: Когда вы определите точные корреляции переменных, вы сможете сэкономить деньги за счет соответствующего планирования.

Лучшее прогнозирование будущего: Хороший регрессионный анализ дает вам представление о будущих возможностях и рисках.

Принятие решений на основе данных: Если вы когда-нибудь задумывались, верна ли ваша интуиция, хороший анализ данных может подтвердить или опровергнуть ее.

Когда вы работаете с регрессионными моделями, попробуйте использовать различные независимые и зависимые переменные, чтобы ответить на ваши вопросы о вашем бизнесе. Если ваши первые попытки не показывают корреляции, попробуйте другие неожиданные переменные, которые могут вас удивить, показав сильную корреляцию. Эта новая информация поможет вам по-другому взглянуть на свой бизнес и поможет вам расти быстрее, чем вы могли себе представить.

Видео:Математика #1 | Корреляция и регрессияСкачать

Ограничения регрессионного анализа

Хотя новый подход к независимым и зависимым переменным может помочь вам быстрее и проще построить свой бизнес, это только в том случае, если данные точны. Регрессионный анализ не лишен подводных камней, рисков и ограничений. Не упустите следующие препятствия, задавая вопросы и отвечая на них с помощью регрессионного прогнозирования:

Предположения: Ваши предположения как владельца бизнеса ограничивают данные, которые вы видите как достаточно важные, чтобы их можно было включить в регрессионную модель.

Неправильные вопросы: Когда ваша регрессионная модель отвечает на вопрос, который на самом деле не влияет на ваш бизнес, она не приведет к необходимым изменениям.

Независимость данных: Если данные независимых и зависимых переменных каким-либо образом перекрываются, целостность вашей регрессионной модели нарушается.

Плохие данные: Если вы собираете слишком обобщенные, слишком конкретные или недостающие данные, ваша модель регрессии будет ненадежной.

Программные ограничения: Программное обеспечение для статистического анализа полезно, но может давать сбои или не предлагать достаточно вариативных вариантов, чтобы соответствовать специфике вашей ситуации.

Поскольку использование регрессионной модели в бизнес-планировании может быть полезным, но не идеальным, важно сочетать регрессионный анализ с другими методами прогнозирования. Рассмотрите возможность включения в свои усилия по прогнозированию некоторых из следующих методов:

Исследования рынка: Опросы и фокус-группы позволяют лучше понять желания и потребности клиентов.

Консультация специалиста: Консультации с различными экспертами в вашей области могут помочь вам составить отчеты с изложением прогнозов.

Индикаторные подходы: Измерение операционного риска поможет вам избежать риска и найти возможности.

Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Корреляция против причинно-следственной связи

Одним из основных соображений при работе с прогнозированием регрессии в бизнесе является то, что ваша базовая модель регрессии показываеткорреляция не причинно-следственная связь. Например, регрессионная модель, показывающая рост продаж снежных шишек в жаркую погоду, показывает, что жаркая погода и продажи тесно связаны. коррелированный. Эта модель не показывает Зачем они тесно взаимосвязаны. Чтобы выяснить причину корреляции, требуется дальнейшее расследование.

Если вы хотите, чтобы ваши маркетинговые усилия говорили о причине увеличения продаж, вам нужно будет провести опросы, беседы и фокус-группы, чтобы определить причину корреляции в бизнес-тенденциях. В случае продажи снежных шишек вы можете обнаружить несколько распространенных причин увеличения продаж снежных шишек в жаркие дни, такие как повышенная жажда, перегрев или больше времени на открытом воздухе с голодными детьми. Выяснение того, почему две переменные тесно взаимосвязаны, поможет вам лучше удовлетворять потребности клиентов и привлекательно рекламировать свой бизнес.

Видео:Точечный прогноз. Интервальный прогноз. Построение уравнения регрессии с помощью анализа данныхСкачать

Регрессионый анализ с целью прогнозирования цен на фондовой бирже. История эксперимента, рабочий пример, результаты

Как всегда, все началось с идеи: а что если поискать корреляцию между индексом ММВБ и ценами акций, входящими в данный индекс, но только использовать цены следующего дня? Например, искать корреляцию между ценой закрытия индекса ММВБ на дату Х и ценой закрытия акции Газпрома на дату (X+1)? Зачем? Затем чтобы, зная цену закрытия индекса ММВБ сегодня, прогнозировать цену закрытия любой акции завтра.

Что получилось, читайте далее…

Статья не является инвестиционной рекомендацией, а скорей результатом индивидуального околоматематического исследования. Не судите строго, мне просто интересно этим заниматься, это мое хобби.

Думаю, следует кратко написать о регрессионном анализе. Википедия конечно дает ответ, но для тех, кто математику подзабыл, читается сложновато. На самом деле все проще, более того, уверен что вы используете регрессию почти ежедневно. Допустим вы любите кофе, часто его пьете и знаете сколько стоит чашечка кофе рядом с вашим домом, офисом и также местах в городе, которые вы посещали. И если вас спросят «сколько может стоить чашечка кофе в центре города?» — вы сможете спрогнозировать цену с определенной точностью. Те, кто занимаются недвижимостью — могут спрогнозировать примерную цену на недвижимость на которой специализируются. Ну и так далее. Причем, чем больше опыт — тем выше ваша точность. Во всех подобных ситуациях наше сознание выполняет функцию регрессионного анализа. Конечно, это достаточно сильное упрощение.

Свою задачу разбил на этапы:

1. Получение массива цен закрытия индекса ММВБ и цен акций, входящих в индекс.
2. По каждой паре «Акция, Индекс» считаем коэффициент корреляции Пирсона, индексы b0 и b1 уравнения регрессионной прямой, рисуем регрессионную прямую.
3. Если коэффициент корреляции больше 0.5, т.е. если данные будут коррелировать, то я могу подставить в полученное уравнение цену закрытия индекса ММВБ на сегодня и спрогнозировать цену интересущей меня акции на завтра… Еще раз акцентирую Ваше внимание, я считаю корреляцию между значением индекса на сегодня и ценой актива(акции) на завтра.
4. Вступаю в клуб анонимных финансовых гуру.

Теперь подробнее о реализации и результатах

Конечно можно было бы воспользоваться услугами брокера и просто выгрузить этот небольшой массив напрямую из торгового терминала (например из Quik). Однако, данные я хочу получать ежедневно и в автоматическом режиме, независимо от того, включаю я терминал или нет. Поэтому самый простой способ, это забирать данные из первоисточника, точнее напрямую с биржы ММВБ. У них есть классное API, вот описание:

Есть небольшое ограничение на количество выдаваемых сервером записей, но я это заметил только на момент получения исторических данных за период с начала года. Обошел посредством деления периода на более короткие промежутки времени. Как говорится, python в помощь.

Как реализован процесс получения и обработки итогов торгов на текущий момент:

1. Каждую ночь, с помощью cron, запускается скрипт который запрашивает данные за прошедший торговый день с сервера биржи ММВБ
2. Полученные данные загружаются в таблицу MySQL на сервере
3. После сохранения данных запускается скрипт пересчета всех коэффициентов

В реализации использовал Flask+MySQL+Requests+Jinja. Графики вывожу с помощью Chart.js Нет, не использовал sklearn для подсчета коэффициентов регрессии, т.к. расчетов по минимуму и требования по производительности не высоки.

Расчеты

По полученным данным считал коэффициент корреляции Пирсона, далее обсчитывал коэффициенты b0 и b1 уравнения регрессионной прямой, используя метод наименьших квадратов. Что не сделано: не считал коэффициент детерминации с целью проверки гипотезы о значимости, а также не проводил расчеты полиноминальной регрессии, только линейной. «Почему так небрежно ?», спросите Вы? Отвечаю: не удовлетворен результатами расчетов, в частности большой величиной среднеквадратичного отклонения, что делает все расчеты весьма приблизительными.

Тем не менее, результаты этой неудачной, но все же работы, Вы можете увидеть вот здесь. Ресурс в публичном доступе, расчеты проводятся автоматически также каждую ночь, без моего участия.

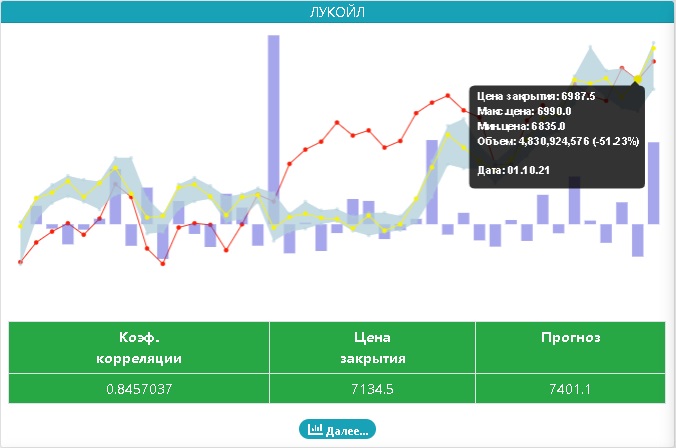
Как это выглядит, хочу показать на примере:

• красная кривая — график цен закрытия индекса ММВБ (IMOEX)
• желтая кривая — график цен закрытия актива (в данном примере «Лукойл»)

Чуть ниже приведена таблица в результатами прогнозирования, причем цветом таблицы выделяется результат прогноза:

1. Серый цвет — нет вменяемой корреляции (коэффициент корреляции в диапазоне [-0.5; +0.5])
2. Красный цвет, корреляция есть, прогноз на понижение
3. Зеленый цвет, корреляция есть, прогноз на рост цены актива

Жмем кнопку «Далее» и видим результаты расчетов и график разброса цен индекса ММВБ к ценам закрытия (на следующий день)

Все здорово, красиво, прямо как по учебнику статистики. Уверен, если постараться, можно даже «добиться» графика нормального распределения остатков. Но, что не так? Ниже графика я привел все расчеты, смотрим на последнюю строку:

Ага, а прогноз у нас 7401.10 руб исходя из текущей цены в 7134.5руб. Простыми словами это звучит так: «прогнозирую рост на 3.7% при точности в плюс/минус 5.4%»

Вот такая вот история неудачи 🙂

Что еще хотелось бы добавить к описанному:

1. Через свою модель считал регрессию не только по отношению к индексу ММВБ, но и к фьючерсам, в том числе и по фьючерсам на конкретный актив. Корреляции особо не увидел;
2. Для себя удалось разрушить некоторые стереотипы аналитиков. В частности о обратной корреляции золота к рынку (когда рынок растет, золото падает и наоборот). Посмотрите на графики золотодобывающих компаний и поймете что это не так;
3. Что касается газпрома и сбербанка — несмотря на хорошую корреляцию, расчеты не объективны, т.к. данные активы занимают существенную долю в индексе (более 30%);
4. Поэтому, в своих расчетах, склонен придерживаться своей «старой позиции»: следовать за большими объемами, крупными сделками (или сериями сделок) на покупку/продажу

Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Регрессионные модели рынка уравнения регрессии

Библиографическая ссылка на статью:
Пивенко К.А., Баженов Р.И. Построение регрессионной модели в среде Gretl на примере рынка поддержанных автомобилей г. Биробиджана и г. Хабаровска // Экономика и менеджмент инновационных технологий. 2015. № 4. Ч. 1 [Электронный ресурс]. URL: https://ekonomika.snauka.ru/2015/04/8362 (дата обращения: 24.01.2022).

В современном мире автомобиль перестал быть роскошью, он стал средством передвижения, доступным многим. Для большинства граждан предпочтительнее купить поддержанный автомобиль, а не новый, только что сошедший с конвейера. Какую сумму правильно будет заплатить за б/у автомобиль? За сколько можно продать свой автомобиль? С этими вопросами сталкиваются многие из нас. Чтобы правильно дать ответ, необходимо учесть определенные параметры: тип кузова, год выпуска, объем двигателя, тип коробки передач, пробег. Используя регрессионную модель в среде Gretl, можем найти зависимость стоимости автомобиля от данных параметров.
Ряд ученых изучает проблемы и методы построения различных регрессионных моделей. Базовые принципы использования метода регрессионного анализа были разработаны С.И. Носковым и М.П. Базилевским [1]. Использовалась множественная регрессия О.В. Гусевым и А.В. Жуковым [2] для идентификации перегрузки сервера. А.А. Жарков и Н.А. Анисимова [3] метод множественной регрессии применили для определения рыночной стоимости квартиры с учетом сроков и условий реализации жилья. Расчет логистических издержек при помощи метода множественной регрессии разработан И.А. Семеновым и А.А. Носковым [4]. С использованием Gretl определяются причины трудового оппортунизма сотрудников Р.З. Мухаметзяновым [5]. Особенности использования среды Gretl в целях построения экономических моделей рассматриваются А.А.Тусковым [6]. Особенности применения программных продуктов Excel и Gretl в рамках эконометрического моделирования рассмотрела Ю.Г.Зарезина [7]. Р.И. Баженовым и др. 10 изучены проблемы использования регрессионных моделей для анализов различных видов. Изучением регрессионного анализа занимаются также зарубежные ученые 16.
По данным сайта www.avito.ru был осуществлен сбор экспериментальных наблюдений. Рассматривались объявления о продаже автомобилей в г.Биробиджан и в г.Хабаровск. Были выбраны следующие критерии: марка, тип кузова, год выпуска, объем двигателя, тип коробки передач, тип привода, пробег, стоимость.
Тип кузова кодируется следующим образом:
1 – седан;
2 – хэтчбэк;
3 – универсал;
4 – кроссовер;
5 – минивэн;
6 – пикап;
7 – внедорожник;
8 – купе.
Тип коробки передач обозначим:
1 – автоматическая;
2 – механическая.
Привод определим:
1 – передний;
2 – задний;
3 – полный.
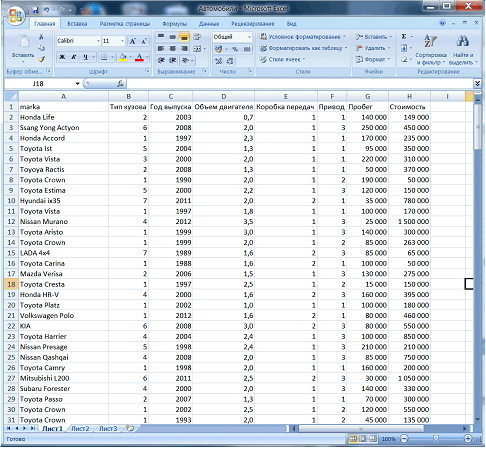
Создадим таблицу данных в MS Excel. Используя данные 200 объявлений (рис.1).

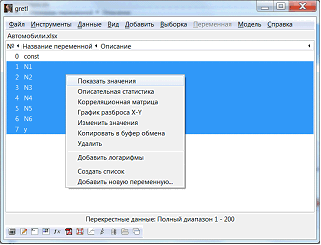
Введем обозначения переменных: тип кузова – х1, год выпуска – х2, объем двигателя – х3, коробка передач – х4, привод – х5, пробег – х6, стоимость – y (рис.2.).

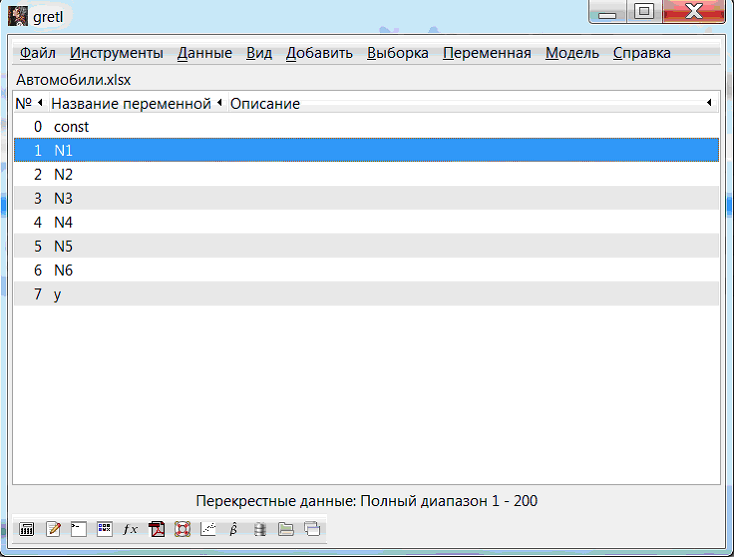
Следующий шаг – открыть данные таблицы Excel в Gretl (рис.3).

В окне программы появляются переменные, которые необходимы, чтобы построить регрессионную модель (рис.4).

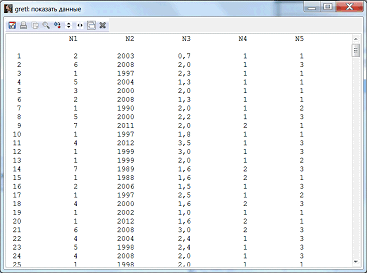
Необходимо просмотреть получившуюся таблицу (рис. 5-6).

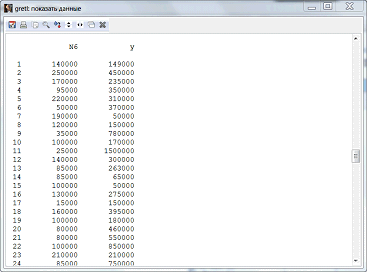
Так как у нас получилось больше шести столбцов данных, то оставшиеся 2 столбца найдем внизу таблицы (рис.7).

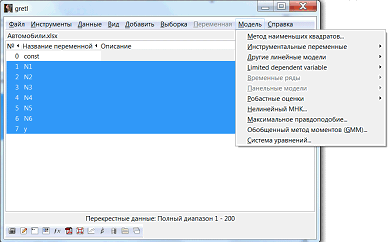
Для решения нашей задачи найдем регрессионную модель, используя метод наименьших квадратов (рис.8).

Перейдем к построению уравнения модели (рис.9)

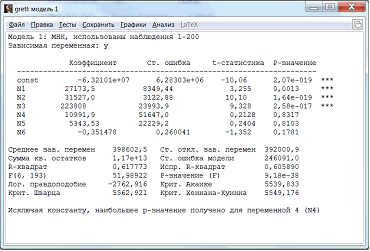
Получившаяся модель и ее описательные статистики показаны на рисунке (рис.10).

По значению R-квадрата можно судить о доле вариации результативного признака с учетом воздействия изучаемых факторов. В данной модели 61,8% вариации переменной Y зависит от влияния включенных факторов, 38,2% обусловлены другими факторами. Если коэффициент выше 80%, то модель считается достаточно хорошей. А у нас слишком низкий R-квадрат. Использование линейной аналитической формы модели может стать вероятной причиной ее слабости. Поэтому найдем другую модель.
При помощи теста на нелинейность можно проверить обоснованность применения степенной модели (рис.11).

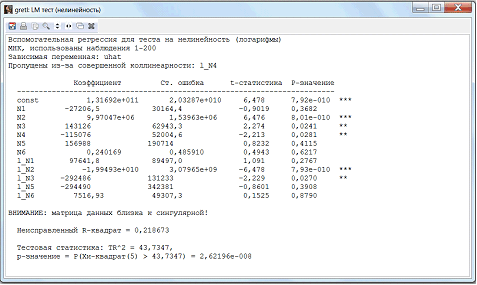
Проверим модель на нелинейность (логарифмы) (рис. 12).

Тест нелинейности для логарифмов (значение p=0,0000001) свидетельствует, что нулевую гипотезу (о линейности аналитической формы) следует отклонить, поскольку значение TR 2 = 43,7347 превышает критическое значение х 2 (1%; 5) = 15,086; по этой причине существуют основания для принятия степенной формы модели (с логарифмированными переменными).
Исследования параметров привели к выводу, что существует логарифмическая зависимость.
Найдем зависимость lny от х ₁ , х ₂ , х ₃ , х ₄ , х ₅ , lnx ₆ (рис.13).

В этой модели R-квадрат у нас уже 75,1%. Значит, модель более точная, чем предыдущая.
Перейдем к решению уравнения

Введем в Excel данные const, х ₁ , х ₂ , х ₃ , х ₄ , х ₅ , х ₆ (рис. 14). Коэффициенты: a – тип кузова, b – год выпуска, с – объем двигателя, d – коробка передач, e – привод, f – пробег.

В ячейку, окрашенную в оранжевый цвет, вводим формулу расчета (рис.15). В таблицу Excel вводим необходимые параметры того автомобиля, который мы хотим купить или продать, в ячейки, окрашенные в синий цвет.

В ячейку, окрашенную в зеленый цвет, вводим формулу расчета стоимости автомобиля. После этого в ячейке, выделенной зеленым цветом, отобразится стоимость данного автомобиля (рис.16).

Если мы хотим узнать стоимость другого автомобиля, то нужно просто в ячейки, окрашенные в синий цвет ввести другие параметры.
Полученную регрессионную модель можно использовать в работе агентств, занимающихся продажей поддержанных автомобилей. Описание принципов построения регрессионной модели может пригодиться в преподавании студентам различных направлений 19.

Библиографический список

1. Базилевский М.П., Носков С.И. Методические и инструментальные средства построения некоторых типов регрессионных моделей // Системы. Методы. Технологии. 2012. №1. С. 80-87.
2. Гусев О.В., Жуков А.В. Способ идентификации перегрузки с использованием множественной регрессии // Информационная среда вуза XXI века. Материалы VII Международной научно-практической конференции. Петрозаводск, 2013. С. 57-61.
3. Жарков А.А., Анисимова Н.А. Механизм формирования стоимости квартир на региональном рынке жилья // Регион: системы, экономика, управление. 2009. № 4. С. 47-53.
4. Семенов И.А., Носков А.А. Модель расчета общих логистических издержек методом множественной регрессии // Вестник Саратовского государственного технического университета. 2011. Т. 4. № 2с. С. 397-400.
5. Мухаметзянов Р.З. Анализ трудового оппортунизма сотрудников // Science time. 2014. №6 (6). С. 132-147.
6. Тусков А.А. Применение Gretl для построения многофакторной модели // Модели, системы, сети в экономике, технике, природе и обществе. 2011. №1. С. 154-159.
7. Зарезина Ю.Г. Особенности применения программных продуктов Excel и Gretl в рамках эконометрического моделирования // Новое слово в науке и практике: гипотезы и апробация результатов исследований. 2015. № 15. С. 223-228.
8. Пронина О.Ю., Баженов Р.И. Исследование методов регрессионного анализа программной среды Eviews // Nauka-Rastudent.ru. 2015. № 1 (13). С. 45.
9. Лагунова А.А., Баженов Р.И. Разработка в среде Gretl регрессионной модели рынка вторичного жилья г. Биробиджана // Nauka-Rastudent.ru. 2015. № 1 (13). С. 40.
10. Муллинов Д.О., Баженов Р.И. Разработка в среде Eviews регрессионной модели рынка гаражных помещений г. Биробиджана // Nauka-Rastudent.ru. 2015. № 1 (13). С. 43.
11. Баженов Р.И. Информационная безопасность и защита информации: практикум. Биробиджан: Изд-во ГОУВПО «ДВГСГА», 2011. 140 с.
12. Vexler V.A., Bazhenov R.I., Bazhenova N.G. Entity-relationship model of adult education in regional extended education system // Asian Social Science. 2014. Т. 10. № 20. С. 1-14.
13. Векслер В.А., Баженов Р.И. Формирование модели обучения взрослых основам информационных технологий: региональный аспект: монография. -Биробиджан: Издательский центр ФГБОУ ВПО «ПГУ им. Шолом-Алейхема», 2014. 126 с.
14. Наумов А.А., Баженов Р.И. О неустойчивости метода нормализации критериев // Современные научные исследования и инновации. 2014. № 11-1 (43). С. 64-68.
15. Baiocchi G., Distaso W. GRETL: Econometric software for the GNU generation // Journal of Applied Econometrics. 2003. Т. 18. №. 1. С. 105-110.
16. Mixon Jr J. W., Smith R. J. Teaching undergraduate econometrics with GRETL // Journal of Applied Econometrics. 2006. Т. 21. №. 7. С. 1103-1107.
17. Баженов Р.И. Об организации научно-исследовательской практики магистрантов направления «Информационные системы и технологии» // Современные научные исследования и инновации. 2014. № 9-2 (41). С. 62-69.
18. Баженов Р.И. Проектирование методики обучения дисциплины «Интеллектуальные системы и технологии» // Современные научные исследования и инновации. 2014. № 5-2 (37). С. 48.
19. Баженов Р.И. Об организации деловых игр в курсе «Управление проектами информационных систем» // Научный аспект. 2014. Т. 1. № 1. С. 101-102.

Количество просмотров публикации: Please wait

Связь с автором (комментарии/рецензии к статье)

Оставить комментарий

Вы должны авторизоваться, чтобы оставить комментарий.

📺 Видео

Простые показатели качества модели регрессии (R2, критерии Акаике и Шварца)Скачать

Линейная регрессия. Оценка качества моделиСкачать

Эконометрика. Множественная регрессия и корреляция.Скачать

Регрессия. Регрессионный анализ в ExcelСкачать

Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать

Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Эконометрика. Нелинейная регрессия. Степенная функция.Скачать

РЕГРЕССИОННЫЙ АНАЛИЗ STATISTICA #12Скачать