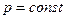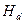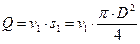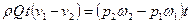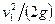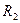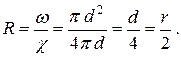Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.
Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.
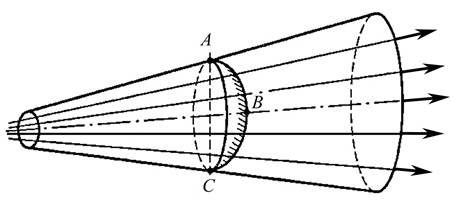
Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости. Живое сечение может быть ограничено твердыми стенками полностью или частично. Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным.
Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.
Содержание статьи
Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.
Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным. Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υср .
Таким образом уравнение расхода для потока будет
υср – средняя скорость потока
F – площадь сечения потока.
Видео:Закон БернуллиСкачать

Уравнение неразрывности потока жидкости
Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.
Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный
а через сечение 2-2 из него же вытекает объем, равный
Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.
Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.
Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки
Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что
т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.
Уравнение неразрывности струи жидкости. Уравнение Бернулли.
Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.
При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.
Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.
Если всё это записать в виде формулы, то
где W – приращение кинетической энергии = m * υ 2 / 2
ΣA – сумма работ действующих сил = P *ΔS
В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.
Теперь рассмотрим обе части этого выражения по порядку.
Приращение кинетической энергии ΔW
В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.
Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.
Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен
масса в этом случае получается равной
Подставляя все это в выражение для кинетической энергии получаем цепочку
ΔW = m * υ 2 2 / 2 — m * υ 2 1 / 2 = ρ * q * ΔТ * υ 2 2 / 2 — ρ * q * ΔТ * υ 2 1 / 2
Работа сил действующих на систему ΣA
Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести AТ равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.
Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.
Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.
Силы давления АД , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.
Суммарно работа сил давления будет
Подставляя в начальное уравнение
Полученные выражения для ΔW и ΣA получаем
Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые
Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:
Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ ρ
Кинетическая удельная энергия = υ 2 / 2
В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.
Видео по теме уравнение неразрывности
Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.
Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.
Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.
Видео:Основы гидродинамики и аэродинамики | условие неразрывностиСкачать

Реферат: Гидравлика 2
| Название: Гидравлика 2 Раздел: Рефераты для военной кафедры Тип: реферат Добавлен 02:34:34 30 мая 2011 Похожие работы Просмотров: 920 Комментариев: 10 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать | |||||||||||||||||||||
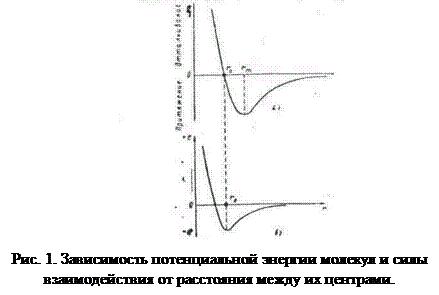 |
вами: температурой, давлением плотностью, вязкостью и др. Поэтому в гидродинамике пользуются экспериментально установленными значениями для этих величин и связями между ними.
Основными параметрами, характеризующими термодинамическое состояние жидкости, являются температура Т, давление р и плотность ρ.
Связь между плотностью, температурой и давлением устанавливается уравнением состояния, которое для реальных жидкостей и газов выводится в кинетической теории. Однако ввиду сложности общего уравнения состояния и затруднительности определения входящих в него констант, для качественного анализа свойств этих сред пользуются приближенными теоретическими или эмпирическими уравнениями.
Другой термодинамической характеристикой жидкости является сжимаемость.
Количественно сжимаемость оценивается изотермическим коэффициентом сжимаемости :
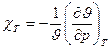
где 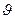
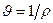
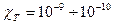
Объем жидкостей и газов изменяется не только при изменении давления, но и при изменении температуры. Как правило, жидкости и газы расширяются с повышением температуры, а плотность их при этом уменьшается. Исключение составляет вода, плотность которой возрастает при повышении температуры от 0 до 4 °С и достигает максимума при 4 °С. Такая аномалия объясняется особенностями молекулярного строения воды.
Количественно изменение объема при изменении температуры и постоянном давлении оценивается коэффициентом теплового объемного расширения
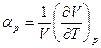
У жидкостей этот коэффициент зависит от температуры и давления, возрастая с повышением первой и уменьшаясь с увеличением второго.
Молекулярные движения в жидкостях и газах обусловливают сопротивление этих сред сдвигающим усилиям.
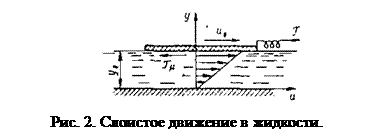 |
Механизм возникновения силы сопротивления можно представить следующим образом. Слой жидкости, прилегающей к пластинке, прилипает к ней и движется вместе с пластинкой со скоростью 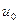
В рассматриваемом случае распределение скоростей линейное. Вследствие действия межмолекулярных связей между движущимися слоями жидкости возникают силы вязкости или внутреннего трения. Ньютон указал на те параметры, от которых зависит величина этой силы 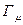
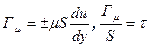
где μ – динамический коэффициент вязкости; S – площадь соприкосновения слоев; 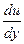
Динамический коэффициент вязкости μ является основной количественной характеристикой вязкости жидкостей и газов.
Наряду с динамическим коэффициентом вязкости в гидрогазодинамике широко используют кинематический коэффициент вязкости ν, определяемый соотношением
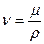
где 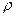
Единицей измерения кинематического коэффициента вязкости служит м 2 /с.
3. Гипотеза сплошности среды.
В гидромеханике рассматриваются макроскопические движения жидкостей и газов, а также силовое взаимодействие этих сред с твердыми телами. При этом, как правило, размеры рассматриваемых объемов жидкостей, газов и твердых тел оказываются несопоставимо большими по сравнению с размерами молекул и межмолекулярными расстояниями. Это естественно, поскольку межмолекулярные расстояния в жидкостях составляют всего 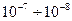
Указанные обстоятельства позволяют ввести гипотезу сплошности изучаемой среды и заменить реальные дискретные объекты упрощенными моделями, представляющими собой материальный континуум, т. е. материальную среду, масса которой непрерывно распределена по объему. Такая идеализация упрощает реальную дискретную систему и позволяет использовать для ее описания хорошо разработанный математический аппарат исчисления бесконечно малых и теорию непрерывных функций.
Параметры, характеризующие термодинамическое состояние, покой или. движение среды, считаются при этом непрерывно изменяющимися по всему объему, занятому средой, кроме, быть может, отдельных точек, линий или поверхностей, где могут существовать разрывы.
Теоретические результаты, подученные для гипотетической сплошной среды, тем лучше совпадут с результатами наблюдений, чем полнее и точнее учтены в ней свойства реальных жидкостей и газов. К сожалению, идеализацию среды во многих случаях не удается ограничить только допущением ее сплошности. Сложность изучаемых явлений заставляет отказываться от учета и некоторых других свойств реальных сред. В зависимости от тех свойств, которые приписываются гипотетической сплошной среде, получают различные ее модели.
Гипотеза сплошности среды означает, что всякий малый элемент объема жидкости считается все-таки настолько большим, что содержит еще очень большое число молекул. Соответственно этому, когда мы будем говорить о бесконечно малых элементах объема, то всегда при этом будем подразумевать «физически» бесконечно малый объем, т. е. объем достаточно малый по сравнению с объемом жидкости, но большой по сравнению с молекулярными расстояниями.
Согласно гипотезе сплошности масса среды распределена в объеме непрерывно и в общем неравномерно. Основной динамической характеристикой среды является плотность распределения массы по объему или просто плотность среды.
Плотность среды 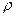
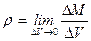
где 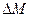
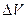
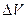
Наряду с плотностью в рассмотрение вводится понятие удельного объема 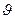
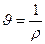
Плотность среды может изменятся от точки к точке и в данной точке со временем, т. е.
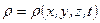
Аналогично для давления имеем 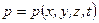
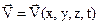
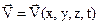
Однако эта функциональная связь не является непосредственной, так как плотность жидкостей и газов определяется фактически значениями термодинамических параметров состояния (р и Т), которые при движении среды зависят от координат (х, у, z) и времени (t ).
Математическое описание движения жидкой среды общими дифференциальными уравнениями, учитывающими все физические свойства, присущие этой среде, оказывается весьма сложной задачей. Если даже ограничится учетом только текучести, вязкости и сжимаемости, то и тогда уравнения движения, выражающие основные законы механики, оказываются настолько сложными, что пока не удалось разработать общих аналитических методов их решения. Применение численных методов интегрирования таких уравнений на базе современных ЭВМ также связано со значительными трудностями. В гидромеханике поэтому широко используют различные упрощенные модели среды и отдельных явлений.
Под моделью реальной среды понимают такую гипотетическую среду, в которой учтены только некоторые из физических свойств, существенные для определенного круга явлений и технических задач. Другие малосущественные свойства среды в модели игнорируются.
Одной из основных в гидромеханике является модель несжимаемой идеальной (или невязкой) жидкости. Так называется гипотетическая сплошная среда, обладающая текучестью, лишенная вязкости и полностью несжимаемая. Эта модель является объектом исследования в разделе гидромеханики «Теория идеальной несжимаемой жидкости». Игнорирование свойств вязкости и сжимаемости сильно упрощает математическое описание движения жидкости и позволяет получить многие решения в конечном замкнутом виде. Несмотря на значительную степень идеализации среды, теория несжимаемой невязкой жидкости дает ряд не только качественно, но и количественно подтверждаемых опытом результатов, полезных для практических приложений. Но не менее существенное значение этой теории состоит в том, что она является базой для других моделей, более полно учитывающих свойства реальных сред. Следует, однако, подчеркнуть, что пренебрежение вязкостью является весьма сильной степенью идеализации, поэтому теория идеальной несжимаемой жидкости может приводит к результатам, резко расходящимся с опытом.
Более полно свойства реальной жидкости учитываются в модели вязкой несжимаемой жидкости, которая представляет собой среду, обладающую текучестью и вязкостью, но абсолютно несжимаемую. Теория вязкой несжимаемой жидкости лишь в ограниченном числе случаев с простейшими граничными условиями позволяет получить точные решения полных уравнений движения. Наибольшее значение в этой теории имеют приближенные уравнения и их решения. Такие уравнения получают путем отбрасывания в полных уравнениях движения тех членов, которые мало влияют на соответствие теоретических решений опыту. Решения приближенных уравнений могут быть как точными, так и приближенными.
Как известно, капельные жидкости являются малосжимаемыми средами, поэтому для широкого круга теоретических и прикладных задач пренебрежение сжимаемостью является вполне допустимой идеализацией и мало влияет на вид получаемых решений и степень совпадения теоретических результатов с данными измерений. Но все же существуют случаи движения жидкостей, которые нельзя достаточно достоверно описать, если не учесть сжимаемость.
Выделим в жидкости некоторый объем. Полная сила, действующая на выделенный объем жидкости, равна интегралу
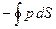
от давления, взятому по поверхности рассматриваемого объема. Преобразуя его в интеграл по объему, имеем:
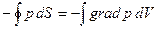
Отсюда видно, что на каждый элемент объема dV жидкости действует со стороны окружающей его жидкости сила 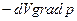
Мы можем теперь написать уравнение движения элемента объема жидкости, приравняв силу — grad p произведению массы 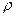
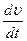
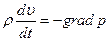
Стоящая здесь производная 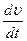
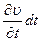
где теперь производная 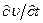
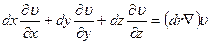
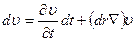
или, разделив обе стороны равенства на dt,
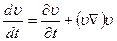
Подставляя полученное соотношение в (14), находим:
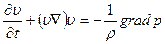
Это и есть искомое уравнение движения жидкости, установленное впервые Л. Эйлером в 1775 г. Оно называется уравнением Эйлера является одним из основных уравнений гидродинамики .
Если жидкость находится в поле тяжести, то на каждую единицу ее объема действует еще сила 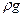
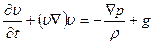
При выводе уравнений движения мы совершенно не учитывал процессов диссипации энергии, которые могут иметь место в текущей жидкости вследствие внутреннего трения (вязкости) в жидкости и теплообмена между различными ее участками. Поэтому все излагаемое здесь относится только к таким движениям жидкостей и газов, при которых несущественны процессы теплопроводности и вязкости; о таком движении говорят как о движении идеальной жидкости.
Отсутствие теплообмена между отдельными участками жидкости (а также, конечно, и между жидкостью и соприкасающимися с нею окружающими телами) означает, что движение происходит адиабатически, причем адиабатически в каждом из участков жидкости. Таким образом, движение идеальной жидкости следует рассматривать как адиабатическое.
При адиабатическом движении энтропия каждого участка жидкости остается постоянной при перемещении последнего в пространстве. Обозначая посредством 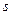
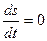
где полная производная по времени означает, как и в (14), изменение энтропии заданного перемещающегося участка жидкости. Эту производную можно написать в виде
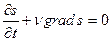
Это есть общее уравнение, выражающее собой адиабатичность движенияидеальной жидкости. С помощью 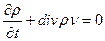
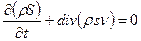
Произведение psv представляет собой «плотность потока энтропии».
Надо иметь в виду, что обычно уравнение адиабатичности принимает гораздо более простую форму. Если, как это обычно имеет место, в некоторый начальный момент времени энтропия одинакова во всех точках объема жидкости, то она останется везде одинаковой и неизменной со временем и при дальнейшем движении жидкости. В этих случаях можно, следовательно, писать уравнение адиабатичности просто в виде
что мы и будем обычно делать в дальнейшем. Такое движение называют изэнтропическим.
Изэнтропичностью движения можно воспользоваться для того, чтобы представить уравнение движения (19) в несколько ином виде. Для этого воспользуемся известным термодинамическим соотношением
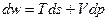
где w – тепловая функция единицы массы жидкости, 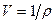
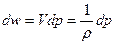
и поэтому 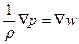
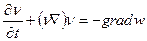
Полезно заметить еще одну форму уравнения Эйлера, в котором оно содержит скорость. Воспользовавшись известной формулой векторного анализа
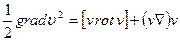
можно написать (29) в виде
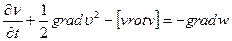
Если применить к обеим строкам этого уравнения операцию rot , то мы получим уравнение
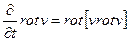
содержащее только скорость.
К уравнениям движения надо добавить граничные условия, которые должны выполняться на ограничивающих жидкость стенках. Для идеальной жидкости это условие должно выражать собой просто тот факт, что жидкость не может проникнуть за твердую поверхность. Это значит, что на неподвижных стенках должна обращаться в нуль нормальная к поверхности стенки компонента скорости жидкости:
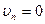
(в общем же случае движущейся поверхности 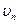
На границе между двумя несмешивающимися жидкостями должны выполняться условие равенства давлений и условие равенства нормальных к поверхности раздела компонент скорости обеих жидкостей (причем каждая из этих скоростей равна скорости нормального перемещения самой поверхности раздела).
Как уже было указано, состояние движущейся жидкости определяется пятью величинами: тремя компонентами скорости 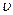
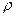
1.Основная формула гидростатики.
Закон Паскаля. Понятие о напоре
Рассмотрим абсолютный покой несжимаемой жидкости в поле силы тяжести .
Уравнение Эйлера (20) принимает вид
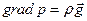
Это уравнение описывает механическое равновесие жидкости. Если внешние силы вообще отсутствуют, то уравнение равновесия гласит просто 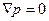
Уравнение (32) непосредственно интегрируется, если плотность жидкости можно считать постоянной вдоль всего объекта, т.е. если не происходит заметного сжатия жидкости под действием внешнего поля. Выберем оси координат, как показано на рис. 2. Поскольку из массовых сил действует только сила тяжести, то
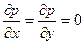
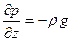

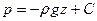
где С – произвольная постоянная.
Эта формула выражает гидростатический закон распределения давления, состоящий в том, что в тяжелой (подверженной действию силы тяжести) несжимаемой жидкости давление линейно зависит от вертикальной координаты.
Чтобы найти постоянную в уравнении (34), надо использовать какое-нибудь граничное условие. Пусть, например, жидкость покоится в резервуаре (см. рис.2) причем на ее свободной поверхности давление равно р0 . Будем это давление называть внешним.
Для точек свободной поверхности можем записать
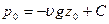
Вычитая это отношение из уравнения (34), находим
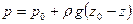
или, обозначив через 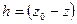
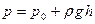
где величина 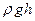
Из этой формулы ясно, что всякое изменение внешнего давления 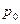
Если жидкость находится в ненапряженном состоянии, т.е. в ней отсутствуют напряжения сжатия, то 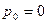
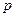
В технике весьма часто представляет интерес избыток давления р над атмосферным 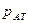
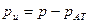
Для произвольной точки М, заглубленной на высоту h под свободную поверхность, избыточное давление равно

отсюда видно, что избыточное давление совпадает с весовым, если давление на свободной поверхности равно атмосферному (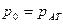
Если все члены формулы (37) разделить на величину 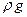
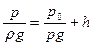
Отсюда следует, что каждому давлению р можно поставить в соответствие линейную величину 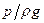
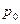
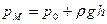
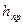
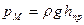
Для трубки П, открытой в атмосферу и называемой пьезометром, получим
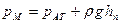
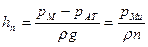
 |
величину 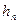
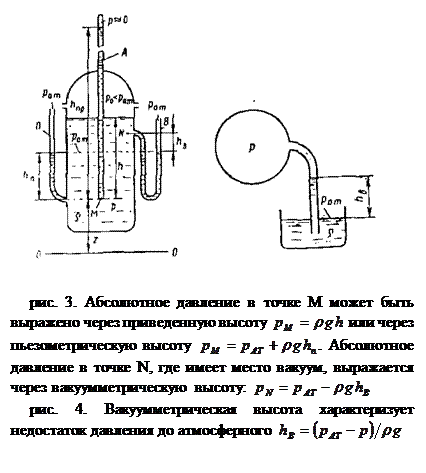
Если давление в точках какого-либо объема жидкости меньше атмосферного (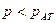
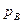
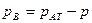
Соответствующая высота называется вакуумметрической:
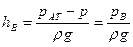
На рис. 3 и 4 показаны вакуумметрические высоты для случаев вакуума в капельной жидкости и газе. Давление измеряется в единицах силы, отнесенных к единице площади. В системе СИ единицей давления служит Н/м 2 = Па (паскаль), а в технической системе – кгс/см 2 = ат (техническая атмосфера). Наряду с этими, как следует из (42) и (44), давление можно, измерять в единицах длины столба данной жидкости.
Общей формулой перевода единиц давления в линейные единицы является
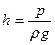
При выражении давления высотой столба жидкости чаще всею применяют метры водяного столба, миллиметры ртутного столба и миллиметры спиртового столба .
Гидростатический закон распределения давления, выраженный формулой (34), справедлив, очевидно, для любого положения координатной плоскости хОу. Эту плоскость называют плоскостью сравнения, а величину 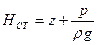
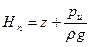
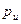
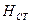

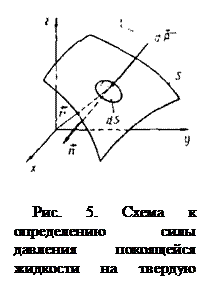
2. Силы давления жидкости на твердые поверхности
В общем случае воздействие жидкости на твердую поверхность S сводится к сумме элементарных сил 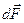
Если 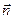
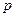
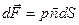
Суммируя систему сил 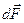
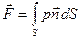
называемого силой давления жидкости на поверхность S , и выражение для главного момента
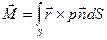
где 
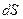
Рассмотрим несколько частных случаев.
2.1.Равномерное давление на плоскую стенку (р = const ., п= const ).
В этом случае суммируемые векторы 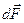
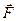
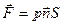
Линия действия силы 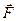
Равномерное давление может создаваться покоящимся газом, так как благодаря малой его плотности можно пренебречь действием массовых сил и считать давление одинаковым во всех точках газа.
Равномерное давление может создаваться и капельной жидкостью, например, при ее воздействии на горизонтальные площадки, в случае абсолютного покоя или движения сосуда с ускорением вверх или вниз.
Величина силы 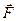
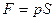
Например, для схемы на рис. 6 давление на дне 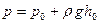
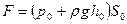
2.2.Сила равномерного давления на криволинейную стенку (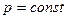
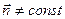
В этом случае элементарные силы 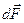
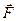
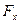
 |
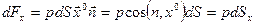
где 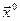
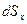
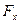
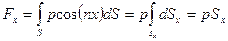
Линия действия силы 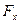
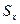
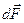
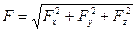
а направление определяется направляющими косинусами
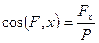
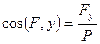
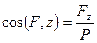
Если составляющие не пересекаются в одной точке, система сводится к силе и моменту.
2.3.Сила неравномерного давления на плоскую стенку (
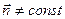
Систему элементарных сил 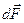
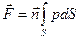

Величина этой силы
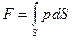
зависит от закона распределения давления Р по площади S. При воздействии на S капельной жидкости эти законы могут быть различными. Их конкретный вид зависит от ориентации площадки и действующих на жидкость массовых сил при абсолютном и относительном покое.
Вычислим силу 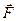
Определим результирующую силу избыточных давлений 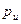
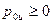
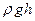
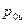
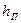
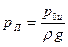
Величину силы вычислим по формуле (53):
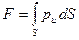
В рассматриваемом случае (см. рис. 8) давление
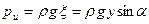
что при подстановке в формулу (53) дает
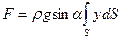
Интеграл 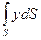
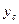
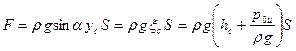
Формула (55) может быть записана в двух видах
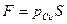
где 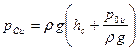
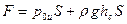
Согласно (56) величина силы избыточного давления покоящейся жидкости на плоскую стенку равна произведению площади стенки на избыточное давление в ее центре тяжести.
Вектор силы 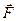
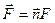
а линия действия этой силы пересекает стенку в некоторой точке D, называемой центром давления. Для отыскания координат этой точки (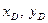
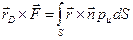
где 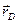
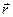
По правилам составления проекций векторного произведения находим
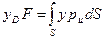
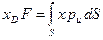
Учитывая выражения (54) и (55), получим
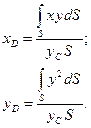
Более удобные выражения для 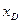
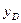
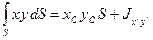
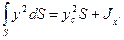
где 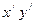
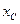
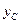


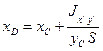
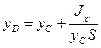
Вторая из формул (60) показывает, что центр давления расположен ниже центра тяжести на величину 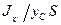
Возвращаясь к формуле (57), заметим, что силу давления в рассматриваемом случае можно получить, складывая независимо вычисленные две силы: 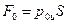
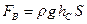
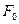
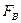
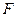
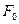
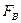
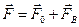
2.4.Неравномерное давление на криволинейную твердую поверхность (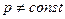
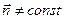
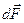
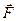

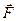
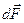
Рассмотрим криволинейную поверхность S, находящуюся под воздействием внешнего избыточного давления 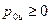
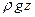
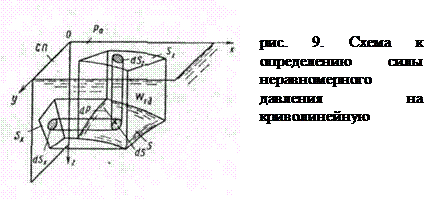 |
Силу весового давления 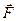

где 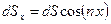

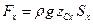
где 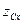


где 
Таким образом, чтобы вычислить горизонтальную проекцию 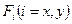
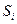
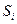
Проекция силы весового давления на вертикальную ось определится соотношением
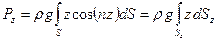
где 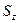
Последний интеграл представляет собой объем тела 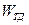
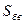
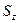
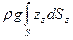
 |
Таким образом, вертикальная проекция силы весового давления на криволинейную поверхность равна весу жидкости в объеме тела давления.
Величина 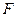
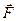
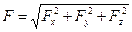
а направление линии ее действия – направляющими косинусами
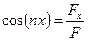
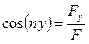
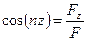
Если 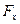
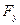
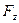
Возможны два случая расположения криволинейной поверхности (рис. 10 а и б) под уровнем жидкости. В первом случае жидкость расположена над твердой поверхностью; тело давления заполнено жидкостью и считается положительным, а вертикальная составляющая силы направлена вниз. Во втором случае тело давления не заполнено жидкостью и считается отрицательным; вертикальная сила давления направлена вверх.
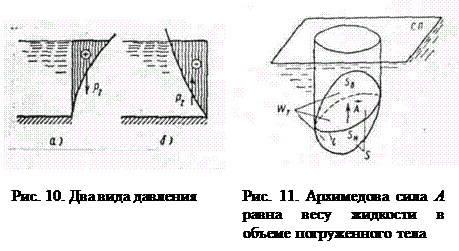
Если криволинейная поверхность S замкнута и полностью погружена под уровень абсолютно покоящейся жидкости (рис. 11), то воздействие жидкости сводится к одной вертикальной силе. Действительно, для любой горизонтальной оси существуют две противоположно направленные и равные по величине силы, действующие на тело; поэтому результирующая горизонтальных сил равна нулю. Чтобы найти вертикальную силу, проектируем S на свободную поверхность жидкости. Проектирующие вертикали отметят на поверхности тела замкнутую линию l , которая делит поверхность на две части 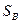

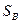

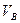
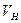
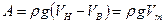
где 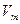
Таким образом, сила давления покоящейся жидкости на погруженное в нее тело направлена вертикально вверх и равна весу жидкости в объеме тела. Этот результат составляет содержание закона Архимеда: сила А называется архимедовой или гидростатической подъемной силой. Если G – вес тела, то его плавучесть определяется соотношением сил А и G. При 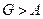
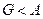
В заключение отметим, что сила давления жидкости по криволинейной поверхности в случаях относительного покоя может быть определена общим способом суммирования элементарных сил давления, применительно к заданной форме поверхности и условиям относительного покоя.
2.1 Основные понятия гидродинамики
Основныеэлементыдвиженияжидкости. Причинами движения жидкости являются действующие на нее силы: объемные или массовые силы (сила тяжести, инерционные силы) и поверхностные силы (давление, трение). В отличие от гидростатики, где основной величиной, характеризующей состояние покоя жидкости, является гидростатическое давление, которое определяется только положением точки в пространстве, т.е. 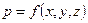
Гидродинамическое давление р – это внутреннее давление. развивающееся при движении жидкости. Скорость движения жидкости в данной точке и – это скорость перемещения находящейся в данной точке частицы жидкости, определяемая длиной пути l , пройденного этой частицей за единицу времени t .
В общем случае основные элементы движения жидкости р и и для данной точки зависят от ее положения в пространстве (координат точки) и могут изменяться во времени. Аналитически это положение гидродинамики записывается так:
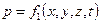
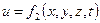
Задачей гидродинамики и является определение основных элементов движения жидкости р и u , установление взаимосвязи между ними и законов изменения их при различных случаях движения жидкости.
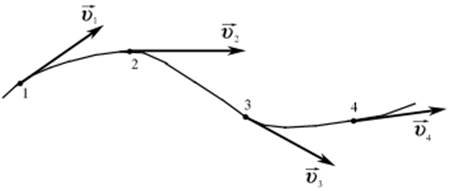
Траекториячастицы.Если в массе движущейся жидкости взять какую-либо частицу жидкости и проследить ее путь за какой-то промежуток времени 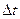
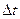
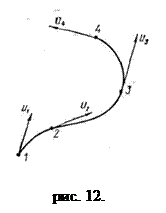
В тот же момент времени t можно взять и другие точки в движущейся жидкости, например, точки 2, 3, 4,. . в которых также можно построить векторы скоростей u 2 ,u 3 , и4 ,… выражающие скорость движения других частиц жидкости в тот же момент.
Можно выбрать точки 1, 2, 3, 4. . . и провести через них плавную кривую, к которой векторы скоростей будут всюду касательны. Эта линия и называется линией тока .
Таким образом, линией тока называется линия, проведенная через ряд точек в движущейся жидкости так, что в данный момент времени векторы скорости частиц жидкости, находящихся в этих точках, направлены по касательной к этой линии . В отличие от траектории, которая показывает путь движения одной частицы жидкости за определенный промежуток времени 
Если в данных точках движущейся жидкости величина и направление скорости и гидродинамическое давление с течением времени не изменяются (такое движение называется установившимся), то и линия тока, и траектория частицы, оказавшейся на ней, совпадают и со временем не изменяются. В этом случае траектории частиц являются и линиями тока.
Элементарная струйка характеризует состояние движения жидкости в данный момент времени t . При установившемся движении элементарная струйка имеет следующие свойства:
1. форма и положение элементарной струйки с течением времени остаются неизменными, так как не изменяются линии тока;
2. приток жидкости в элементарную струйку и отток из нее через боковую поверхность невозможен, так как по контуру элементарной струйки скорости направлены по касательной;
3. скорость и гидродинамическое давление во всех точках поперечного лечения элементарной струйки можно считать одинаковым ввиду малости площади 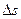
Поток.Совокупность элементарных струек движущейся жидкости, проходящих через площадку достаточно больших размеров, называется потоком жидкости . Поток ограничен твердыми поверхностями, по которым происходит движение жидкости (труба), и атмосферой (река, лоток, канал и т.п.).
2.2 Понятие о потоке жидкости.
Гидравлическиеэлементыпотока. Живым сечением называется поверхность в пределах потока, проведенная перпендикулярно к линиям тока (элементарным струйкам) . В общем случае эта поверхность криволинейная (на рис. 14 поверхность ABC). Однако в большинстве случаев практической гидравлики поток жидкости можно представить параллельно-струйным или с очень малым углом расхождения струек, а за живое сечение принять плоское поперечное сечение потока (нарис. 14 плоскость АС). Площадь живого сечения обозначается 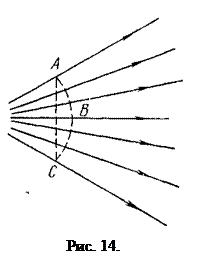
Смоченным периметром называется длина части периметра живого сечения, в пределах которой поток соприкасается с твердыми внешними стенками . Смоченный периметр обозначают буквой П .
Гидравлическим радиусом называется отношение площади живого сечения к смоченному периметру :
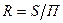
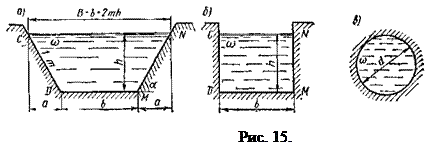
На рис. 15 приведены примеры поперечных сечений потока: а) трапецеидальное; б) прямоугольное; в) круговое.
Для кругового сечения, заполненного жидкостью полностью (рис. 15, в ): 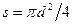
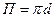
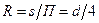
Расходжидкости и средняяскорость. Расходом жидкости называется количество жидкости, проходящей через данное живое сечение потока в единицу времени .
Расход потока жидкости обозначают Q, а элементарной струйки – 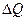
 |
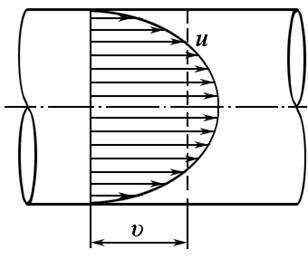
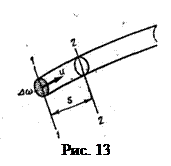
Рассмотрим элементарную струйку (рис. 13) с поперечным сечением 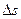
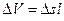
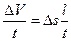
но 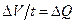
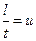

т. е. расход элементарной струйки равен площади ее поперечного сечения, умноженной на скорость в этом сечении . Поток жидкости в данном живом сечении представляет совокупность (сумму) большого числа элементарных струек, заполняющих сплошь площадь живого сечения, поэтому для определения расхода потока через живое сечение s необходимо взять сумму расходов 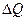
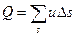
В общем случае, чтобы воспользоваться формулой (67б) для определения расхода потока, надо знать закон распределения скоростей по живому сечению, который очень сложен или вообще неизвестен. Поэтому для практических расчетов вводится понятие средней скорости потока.
На рис. 16 представлен график (эпюра) распределения действительных скоростей в точках живого сечения потока, из которого видно, что скорости по сечению распределяются неравномерно. При действительных скоростях через живое сечение проходит определенный расход Q. Можно найти некоторую постоянную для всех точек сечения фиктивную скорость, при которой через данное сечение проходил бы тот же самый расход, что и при действительных скоростях движения жидкости. Эта скорость v будет средней из действительных скоростей. Подставляя в формулу (67б) скорость v получим 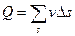

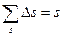
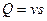
т. е. расход жидкости в данном сечении потока равен произведению средней скорости движения жидкости, умноженной на площадь живого сечения.
Итак, средней скоростью потока в данном сечении v называется такая одинаковая для всех точек живого сечения скорость движения жидкости, при которой через это живое сечение проходит тот же расход Q , что и при действительных скоростях движения жидкости и .
Из формулы (68) можно написать
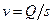
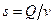
Формулы (68), (68′) и (68″) используются при решении основных гидравлических задач, связанных с потоком жидкости. Их следует четко знать и запомнить.
2.3. Виды движения жидкости
Установившимся стационарным движением жидкости называется такое движение, при котором в каждой данной точке основные элементы движения жидкости – скорость движения и и гидродинамическое давление р не изменяются с течением времени, т.е. зависят только от координат точки . Аналитически это условие запишется так:
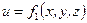
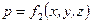
Неустановившимся (нестационарным) движением жидкости называется такое движение, при котором в каждой данной точке основные элементы движения жидкости – скорость движения и и гидродинамическое давление р – постоянно изменяются, т.е. зависят не только от положения точки в пространстве, но и от времени 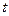


Примером установившегося движения может быть: движение жидкости в канале, в реке при неизменных глубинах, истечение жидкости из резервуара при постоянном уровне жидкости в нем и др. Неустановившееся движение – это движение жидкости в канале или реке при переменном уровне или при опорожнении резервуара, когда уровень жидкости в нем непрерывно изменяется.
В дальнейшем будет изучаться главным образом установившееся движение жидкости и в отдельных случаях будут разбираться примеры неустановившегося движения.
Установившееся движение в свою очередь подразделяется на равномерное и неравномерное .
Равномерным называется такое установившееся движение, при котором живые сечения вдоль потока не изменяются: в этом случае 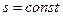

Установившееся движение называется неравномерным, когда распределение скоростей в различных поперечных сечениях неодинаково; при этом средняя скорость и площадь поперечного сечения потока могут быть и достоянными вдоль потока . Примером неравномерного движения может быть движение жидкости в конической трубе или в речном русле переменной ширины.
Напорным называется движение жидкости, при котором поток полностью заключен в твердые стенки и не имеет свободной поверхности. Напорное движение происходит вследствие разности давлений и под действием силы тяжести. Примером напорного движения является движение жидкости в замкнутых трубопроводах (например, в водопроводных трубах).
Безнапорным называется движение жидкости, при котором поток имеет свободную поверхность. Примером безнапорного движения может быть: движение жидкости в реках, каналах, канализационных и дренажных трубах. Безнапорное движение происходит под действием силы тяжести и за счет начальной скорости. Обычно на поверхности безнапорного потока давление атмосферное.
Следует отметить еще один вид движения: свободную струю. Свободной струей называется поток, не ограниченный твердыми стенками. Примером может служить движение жидкости из пожарного брандспойта, гидромонитора, водопроводного крана, из отверстия резервуара и т. п. В этом случае движение жидкости происходит по инерции (т. е. за счет начальной скорости) и под действием силы тяжести.
Для упрощения выводов, связанных с изучением потока жидкости, вводится понятие о плавно изменяющемся движении жидкости.
Плавно изменяющимся называется такое движение жидкости, при котором кривизна струек незначительна (равна нулю или близка к нулю) и угол расхождения между струйками весьма мал (равен нулю или близок к нулю), т. е. практически поток жидкости мало отличается от параллельноструйного. Это предположение вполне оправдывается при изучении многих случаев движения жидкости в каналах, трубах и других сооружениях.
Отметим следующие свойства потока при плавно изменяющемся движении:
1. поперечные сечения потока плоские, нормальные к оси потока;
2. распределение гидродинамических давлений по сечению потока подчиняется закону гидростатики, т.е. гидродинамические давления по высоте сечения распределяются по закону прямой. Это свойство легко можно доказать, если внутри потока выделить частицу жидкости и спроектировать все действующие на нее силы на плоскость живого сечения. Вследствие того, что скорости и ускорения в этом случае будут перпендикулярны сечению, силы инерции в уравнение не войдут; поэтому уравнение равновесия и закон распределения давления в плоскости живого сечения не будет отличаться от такового для жидкости, находящейся в покое;
3. удельная потенциальная энергия (т. е. потенциальная энергия единицы веса жидкости) по отношению к некоторой плоскости сравнения для всех точек данного сечения потока жидкости есть величина постоянная.
2.4. Уравнение неразрывности установившегося движения жидкости
При рассмотрении движения жидкости считают, что в потоке жидкость сплошь заполняет занимаемое ею пространство без образования пустот, т.е. движение жидкости происходит неразрывно. В этом случае справедливо уравнение неразрывности движения, выводимое на основе закона сохранения массы. Получим вначале уравнение неразрывности при установившемся движении жидкости для элементарной струйки.
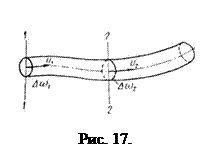
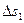

Затем возьмем сечение 2-2 в этой же струйке с площадью сечения 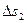
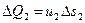
Но по свойству элементарной струйки приток и отток жидкости через ее боковую поверхность невозможен (см. § 2.1); кроме того, в отсеке 12, который сохраняет неизменные размеры, не образуется пустот и не происходит переуплотнений; значитколичества жидкости, протекающей н единицу времени через сечения 1-1 и 2-2 , должны быть одинаковы, т.е. 
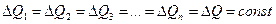
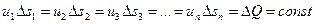
Это и есть уравнение неразрывности (сплошности) для элементарной струйки, которое читается так: элементарный расход жидкости 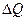
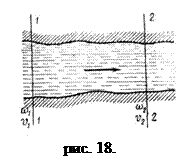

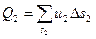
Но поскольку скорости касательны к боковой поверхности потока, то в отсек между сечениями 1 -1 и 2-2 через боковую поверхность движения жидкости не происходит; не изменяется и объем отсека. Следовательно, в отсек через сечение 1-1 поступает столько же жидкости, сколько за то же время выходит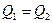

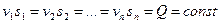
Это и есть уравнение неразрывности для потока жидкости , которое читается так: расход жидкости через любое сечение потока при установившемся движении есть величина постоянная . Из уравнения (69) для двух сечений можно написать
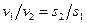
т.е. средние скорости потока обратно пропорциональны площадям соответствующих живых сечений.
2.5. Уравнение Д. Бернулли
Уравнение Даниила Бернулли является основным уравнением гидродинамики. Ниже разбирается это уравнение для установившегося плавно изменяющегося движения жидкости, с помощью которого решаются основные задачи гидродинамики. Введем понятия удельной энергии элементарной струйки и потока жидкости.
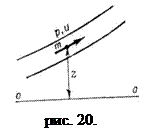
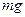
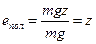
Масса жидкости занимает некоторый объем V , находящийся под давлением р. Потенциальная энергия давления равна р V . Удельная же потенциальная энергия давления равна потенциальной энергии pV , деленной на силу тяжести данного объема g V , т. е.
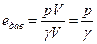
Полный запас удельной потенциальной энергии массы жидкости равен их сумме, т. е. 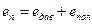
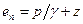
Кроме того, масса жидкости т движется со скоростью и и обладает кинетической энергией 
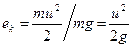
Складывая выражения (в) и (г), получим выражение полной удельной энергии элементарной струйки
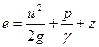
Здесь 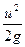
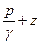
Полная удельная энергия потока Е складывается из удельной потенциальной энергии 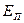
Для случая установившегося плавно изменяющегося движения жидкости удельная потенциальная энергия во всех точках живого сечения одинакова и равна
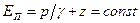
Поток жидкости рассматривается как совокупность п элементарных струек, каждая из которых обладает своей удельной кинетической энергией 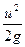
Определим среднее значение этой величины в сечении потока. Для этого действительные скорости элементарных струек u 1 , u 2 , . ип заменим средней скоростью потока v ;тогда среднее значение удельной кинетической энергии потока в данном сечении равно
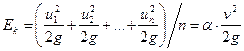
Здесь a – коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечению потока (или корректив кинетической энергии).
Безразмерный коэффициент a представляет собой отношение действительной кинетической энергии потока к кинетической энергии, вычисленной по средней скорости. Если эпюра скоростей в сечении потока близка к прямоугольной, т.е. скорости в разных точках близки к средней, то коэффициент Кориолиса a близок к единице. Если же скорости в сечении значительно различаются между собой, то и коэффициент a оказывается значительно больше единицы.
Рассмотрим, например, поток глубиной Н = 6м, в сечении которого скорости распределены по треугольнику, т.е. у дна скорость равна нулю и к поверхности нарастает по закону прямой до наибольшего значения ипов = 3 м/сек. Средняя скорость v = 1,5 м/сек, а соответствующая ей кинетическая энергия

Оценим кинетическую энергию потока точнее. Для этого возьмем три точки на высоте h 1 = 1м; h 2 = 3 м и h 3 = 5 м, которые лежат посредине слоев равной высоты по 2 м каждый. Скорость в этих точках соответственно и1 = 0,5; и2 = 1,5 и и3 = 2,5 м/сек. Вычислим кинетическую энергию по этим трем скоростям
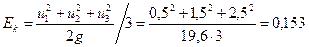
что больше, чем по средней скорости.
Коэффициент Кориолиса получается
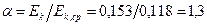
На основе обработки многочисленных данных, полученных на реках и каналах, установлено, что для больших открытых потоков 

В дальнейшем, за исключением особо оговоренных случаев, для упрощения расчетов будем принимать 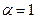
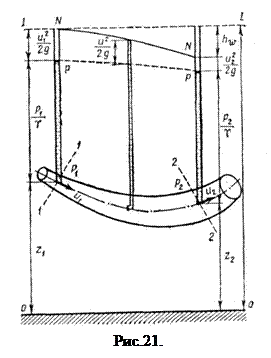 |
Складывая удельную кинетическую и удельную потенциальную энергии потока, получим формулу полной удельной энергии потока
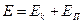
а учитывая выражения (е) и (д), имеем

т.е. полная удельная энергия потока равна сумме удельной кинетической и удельной потенциальной (давления и положения) энергий потока. Напомним, что все выводы сделаны для установившегося, плавно изменяющегося движения жидкости.
УравнениеД. Бернуллидляэлементарнойструйки. Выделим в установившемся потоке реальной жидкости элементарную струйку (рис. 21) и определим удельную энергию жидкости в двух произвольных сечениях 1-1 и2-2. Высоты положения центров первого и второго сечений будут соответственно z 1 и z2 ; гидродинамическое давление и этих же точках р1 и р2 скорости течения – и1 и и2 . Тогда полная удельная энергия элементарной струйки в сечении 1 -1 на основании формулы (71)равна

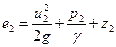
Практически всегда 


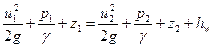
Уравнение (73) и есть уравнение Д. Бернулли для элементарной струйки реальной жидкости при установившемся движении, которое устанавливает связь между скоростью движения, давлением в жидкости и положением точки в пространстве. Оно справедливо для любых двух сечений, так как сечения 1-1 и 2-2 были взяты произвольно. Уравнение (73) можно изобразить и графически (рис. 21).Если соединить уровни жидкости в пьезометрах, присоединенных к нескольким сечениям, получим некоторую линию р-р, которая называется пьезометрической линией и показывает изменение удельной потенциальной энергией по длине элементарной струйки. Если соединить точки, которые в каждом сечении вертикали изображают полную удельную энергию (а такие точки действительно можно получить, о чем см. ниже), получим некоторую линию N — N , которая называется напорной линией или линией энергии; она показывает изменение полной удельной энергии по длине струйки. Тогда расстояние по вертикали в любом сечении между горизонтальной плоскостью I —I , соответствующей начальному запасу удельной энергии в первом сечении, и напорной линией N — N дает величину потерь энергии hw на преодоление сил сопротивления на участке от первого сечения до данного сечения, а расстояние между напорной и пьезометрической линиями – удельную кинетическую энергию в данном сечении u 2 /2 g .
Для идеальной жидкости, где отсутствуют силы трения, в уравнении (IV.7) hw = 0 и уравнение Бернулли принимает вид
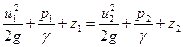
Но так как сечения 1-1 и2-2 взяты произвольно, то в общем виде уравнение Бернулли для элементарной струйки идеальной жидкости записывается так:
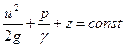
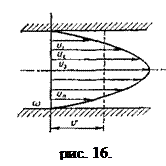
УравнениеД. Бернуллидляпотока.Рассмотрим поток при установившемся, плавно изменяющемся движении (рис. 22). Выберем произвольно два сечения 1-1 и 2-2 , по осям которых соответственно имеем z 1 и z 2 – вертикальные координаты оси потока над произвольной плоскостью сравнения о-о, р1 и p 2 гидродинамические давления, в тех же точках v 1 и v 2 – средние скорости в сечениях 1-1 и 2-2 .
Полную удельную энергию потока определяем по формуле (72): сечение 1-1
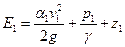
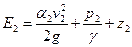
Очевидно 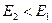
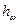
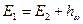
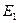
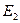
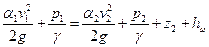
Уравнение (74) называется уравнением Д. Бернулли для потока жидкости и является основным уравнением гидродинамики; с его помощью получены многие расчетные формулы и решается ряд практических задач. Уравнение Бернулли устанавливает математическую связь между основными элементами движения жидкости, т. е. средней скоростью и гидродинамическим давлением.
2.6. Истолкование уравнения Д. Бернулли
Рассмотрим смысл уравнения Бернулли с точек зрения гидравлической, геометрической и энергетической.
ГидравлическоеистолкованиеуравненияД. Берн у л л и. С точки зрения гидравлики каждый член уравнения Бернулли (74) имеет свое название, а именно:
1. Первый член правой и левой частей уравнения Бернулли 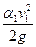
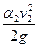
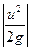
2. Второй член правой и левой частей уравнения 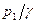

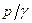
3.Третий член правой и левой частей уравнения 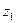
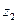
4. Четвертый член правой части уравнения hw называется потерей напора при движении жидкости между сечениями 1-1 и 2-2 .
Напомним, что сумма пьезометрической высоты 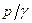
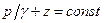
Сумма скоростного напора 

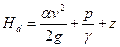
Учитывая выражение (75), уравнение Д. Бернулли можно написать в следующем виде:
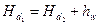
Таким образом, с гидравлической точки зрения уравнение Д. Бернулли может быть прочитано так: гидродинамический напор в данном сечении потока жидкости равен гидродинамическому напору в другом сечении (лежащем ниже по течению) плюс потеря напора между этими сечениями.
ГеометрическоеистолкованиеуравненияД. Берн у л л и. В связи с тем, что все члены уравнения Бернулли имеют линейную размерность, его можно представить графически (см. рис. 22), отложив в каждом сечении от плоскости сравнения о-о по вертикали отрезки, выражающие в определенном масштабе 
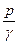
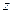
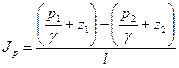
т.е. пьезометрическим уклоном Jp называется безразмерная величина. показывающая изменение пьезометрического напора, приходящееся на единицу длины потока. Пьезометрический уклон Jp может быть величиной положительной – линия рр понижается по направлению движения, когда скорости вдоль потока растут; или отрицательной – линия рр повышается по направлению движения, когда скорости вдоль потока уменьшаются.
Проведя между сечениями1-1 и 2-2 линиюNN по верхним точкам гидродинамического напора, получим так называемую напорную линию, которая показывает изменение гидродинамического напора по длине потока. Поделив разность гидродинамических напоров в двух сечениях на расстояния между ними, получим средний гидравлический уклон
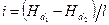
но 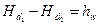
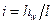
т. е гидравлическим уклоном потока называется безразмерная величина, показывающая изменение гидродинамического напора на единицу длины потока. Заметим, что I может быть только положительной величиной, так как напорная линияNN всегда понижается ввиду того, что потери напора по длине потока неизбежны.
Таким образом, с геометрической точки зрения уравнение Д. Бернулли можно прочитать так: напорная линия по длине потока всегда понижается, так как часть напора тратится на преодоление трения по длине поток.
Частныйслучай.При равномерном движении, когда скорость по длине потока не изменяется, напорная NN и пьезометрическая рр линиипараллельны, так как 
ЭнергетическоеистолкованиеуравненияД. Берн у л л и. Принимая во внимание изложенное в § 2.5 и формулу (72), сумму членов уравнения Бернулли с энергетической точки зрения можно представить как сумму удельной кинетической 

Гидравлический уклон с энергетической точки зрения необходимо рассматривать как уменьшение полной удельной энергии на единицу длины потока.
2.7. Практическое применение уравнения Д. Бернулли
При применении уравнения Д. Бернулли для решения практических задач гидравлики следует помнить два основных условия:
1. уравнение Бернулли может быть применено только для тех живых сечений потока, в которых соблюдаются условия плавно изменяющегося движения. На участках между выбранными сечениями условия плавно изменяющегося движения могут и не соблюдаться;
2. гидродинамическое давление 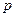
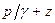

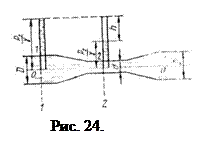
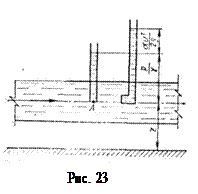
В основной трубе сечение 1-1 и в суженном сечении сечении 2-2 присоединены пьезометры, по показаниям которых можно определить расход жидкости в трубе Q.
Выведем общую формулу водомера для определения расхода в трубе. Составим уравнение Бернулли для точек, расположенных в центре тяжести сечений 1-1 перед сужением и 2-2 в горловине, приняв плоскость сравнения по оси трубы о-о. Для наших условий 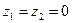
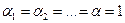
Потери напора в сужении ввиду малости расстояния между сечениями считаем равными нулю, т.е. 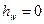
Тогда уравнение Бернулли (74) запишется так:
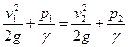
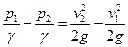
Но из рис. 24 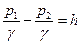
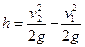
В уравнении (а) две неизвестные величины 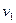
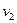
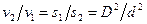

Подставляя 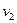

Отсюда скорость течения в основной трубе (сечение 1-1 ) равна
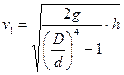
расход жидкости в трубе по формуле IV.2:
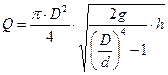
Обозначим постоянную величину для данного водомера через К
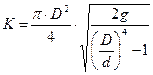
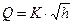
Однако при выводе этой формулы не учитывались потери напора в водомере, которые в действительности будут. С учетом потерь напора формула расхода водомера Вентури запишется так:
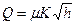
где 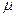
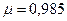
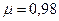
Таким образом, для определения расхода в трубе достаточно замерить разность уровней воды в пьезометрах и подставить ее значение в формулу (80).
2.8. Виды гидравлических сопротивлений и потери напора
Выше были получены два основных уравнения гидродинамики: уравнение сохранения энергии (уравнение Д. Бернулли), связывающее средние скорости и давления, и уравнение неразрывности потока (сохранения массы) для несжимаемой жидкости, которые были записаны в следующем виде:
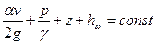
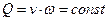
При решении некоторых задач вполне достаточно этих уравнений, если пренебречь потерями энергии (напора) hw ,так как расход Q и полный напор H обычно заданы или могут быть определены.
Но большинство задач нельзя решить, если пренебречь потерями напора hw . В таких случаях имеются два уравнения и три неизвестных v , р и hw .
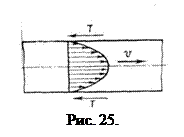
При движении потока между жидкостью и стенками, ограничивающими поток, возникают силы сопротивления. Кроме того, вследствие вязкости жидкости между ее отдельными слоями возникают силы сцепления, которые также затормаживают движение потока. Скорость движения частиц жидкости уменьшается по мере по мере удаления от оси потока к стенкам трубы, лотка и т. д. Равнодействующая сил сопротивления параллельна оси потока и направлена в сторону, противоположную направлению движения (рис. 25).
Для преодоления сил гидравлического трения и сохранения поступательного движения жидкости необходимо приложить силу, направленную в сторону движения и равную силам сопротивления. Работу этой силы называют потерями напора по длине потока (путевые потери напора) и обозначают через 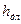
Сети трубопроводов, распределяющие или отводящие жидкость от потребителей, меняют свой диаметр (сечение); на сетях устраиваются повороты, ответвления, устанавливаются запорные устройства и т. п. В этих местах поток меняет спою форму, резко деформируется. Вследствие изменения формы возникают дополнительные силы сопротивления, так называемые местные сопротивления. На их преодоление расходуется напор. Напор, затрачиваемый на преодоление местных сопротивлений, называют местными потерями напора и обозначают через 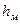
Общие потери напора равны сумме потерь напора по длине и местных
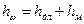
Размерность потерь напора такая же, как и напора, т. е. метры столба жидкости.
2.9. Режимы движения жидкости. Число Рейнольдса.

Ламинарный режим движения можно наблюдать чаще у вязких жидкостей, таких как нефть, масла и т. п.
Турбулентным называют режим, при котором наблюдается беспорядочное движение, когда частицы жидкости движутся по сложным траекториям и слои жидкости постоянно перемешиваются друг с другом (рис. 26, б).
Существование двух режимов движения жидкости было замечено в 1839 г. Хагеном и в 1880 г. Д. И. Менделеевым.
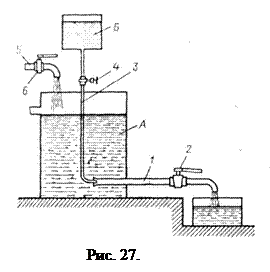
Установка Рейнольдса для исследования режимов движения жидкости пред ста влена на рис. 27. Сосуд А заполняется испытуемой жидкостью. К сосуду А в нижней его части присоединена стеклянная трубка 1 с краном 2 , которым регулируется скорость течения в трубке. Над сосудом А расположен сосуд Б сраствором краски. От сосуда Б отходит трубка 3 скраном 4. Конец трубки 3 заведен в стеклянную трубку 1. Для пополнения сосуда А служив трубка 5 с запорным устройством 6.
При ламинарном режиме движения жидкости по трубке 1 струйка раствора краски, истекающей из трубки 3 , имеет вид четко вытянутой нити вдоль трубки 1 .
По мере открытия крана 2 увеличивается скорость движения и режим движения переходит в турбулентный, при этом струйка приобретает волнообразный характер, а при еще большей скорости совсем размывается и смешивается с жидкостью в трубке. При постепенном закрытии крана эти явления протекают в обратном порядке, т. е. турбулентный режим сменяется ламинарным.
Опыты показали, что переход от турбулентного режима к ламинарному происходит при определенной скорости (эта скорость называется критической ),которая различна для разных жидкостей и диаметров труб; при этом критическая скорость растет с увеличением вязкости жидкости и с уменьшением диаметра труб.
Рейнольдсом и рядом других ученых опытным путем было установлено, что признаком режима движения является некоторое безразмерное число, учитывающее основные характеристики потока
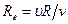
где 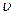
Это отношение называется числом Рейнолъдса. Значение числа Re , при котором турбулентный режим переходит в ламинарный, называют критическим числом Рейнолъдса ReKp .
Если фактическое значение числа Re , вычисленного по формуле (82), будет больше критического Re > ReKp – режим движения турбулентный, когда Re 2 ; 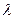
Впервые формула (84) была получена эмпирическим путем в XIX в. и названа формулой Дарси-Вейсбаха. В дальнейшем указанная формула проверена теоретически на основе метода анализа размерностей.
В уравнении (84) остается не выясненным смысл безразмерного коэффициента 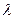
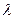
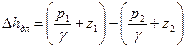
При горизонтальном расположении трубы 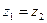
 |

Для уточнения вопроса о потерях напора выделим в трубопроводе между сечениями 1-1 и 2-2 соосный цилиндр с радиусом а и длиной l (рис. 31).
Как оговорено выше, распределение скоростей в сечениях 1-1 и 2-2 одинаково, частицы жидкости двигаются без ускорений.
Напишем уравнение динамического равновесия рассматриваемого цилиндра
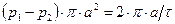
где 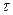
Поделив обе части уравнения на 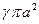
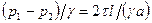
Подставляя из уравнения (86) значение 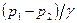
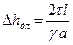
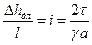
Выразим 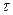
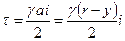
(так как 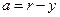
У стенки трубы, где 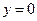
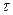
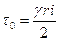

Уравнение (91) есть общее выражение потерь напора при равномерном движении жидкости в трубах. Подставляя в уравнение (91) значения 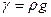
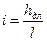

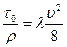
Замечаем, что 
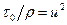
где 
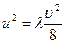
Из уравнения (94) находим, что

Таким образом, коэффициент гидравлического трения 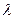
Потеринапораприламинарномдвижении.На основе изложенного выше для потерь напора по длине при ламинарном режиме движения жидкости в трубе получено следующее уравнение:
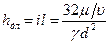
где 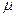
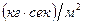
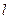
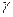
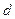
Так как 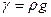
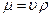
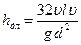
Выражение (97) называют формулой Пуазейля-Гагена (по имени ученых, получивших это уравнение).
Формула (97) показывает, что при ламинарном режиме потери напора пропорциональны средней скорости и не зависят от состояния стенок трубопровода.
Приравняв правые части уравнения Дарси-Вейсбаха (84) и выражения (97), получим
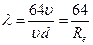
Таким образом, коэффициент гидравлического трения при ламинарном режиме обратно пропорционален числу Рейнольдса.
Потеринапорапритурбулентномдвижении.В инженерной практике чаще встречается турбулентный режим движения жидкости в трубах, которые труднее исследовать теоретически. Этот вопрос подвергся наиболее широким опытным исследованиям как со стороны советских, так и зарубежных ученых. Из-за сложности процессов, протекающих при турбулентном режиме, до сих пор не создано окончательной теории, которая бы вытекала из основных уравнений гидродинамики и согласовывалась с опытом. Напомним, что при турбулентном режиме наблюдается интенсивное вихреобразование, частицы жидкости описывают сложные траектории, местные скорости меняются во времени даже при постоянном расходе. Это явление называется пульсацией скорости. Часть кинетической энергии жидкости переходит в тепловую. Установившегося движения в строгом смысле нет. Поэтому введено понятие об осредненной скорости.
Мгновенные скорости пульсируют около своего осредненного значения, которое за достаточно длительный промежуток времени остается постоянным; это значение и называется осредненной скоростью. В дальнейшем, говоря о скоростях, рассматривая турбулентное движение, будем подразумевать осредненные скорости.
Опытами установлено, что закон распределения осредненных скоростей по сечению и потери напора зависят от диаметра труб, средней скорости, вязкости жидкости и шероховатости стенок труб. В свою очередь характер шероховатости зависит от материала стенок труб, степени обработки, а последние определяют высоту выступов, их густоту и форму. Для приближенной оценки введено понятие средней высоты бугорков (выступов) шероховатости, называемой абсолютной шероховатостью и обозначаемой k . Очевидно, что чем меньше диаметр, тем быстрее частицы жидкости совершат пробег от центра трубопровода к стенкам и встретятся с бугорками шероховатости, и, отражаясь от них, вызовут возмущения в потоке жидкости. Следовательно, частота вихреобразования при малых диаметрах труб больше, и шероховатость той же высоты проявляется сильнее. Поэтому введено понятие относительной шероховатости, т. е. отношение абсолютной шероховатости к диаметру трубы 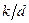
Экспериментами установлено, что коэффициент гидравлического трения 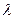
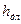
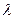
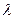
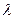
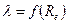
С увеличением числа Рейнольдса ламинарный слой становится тоньше и не покрывает выступов шероховатости; при этом от выступов шероховатости начинают отрываться вихри, и свойства поверхности оказывают влияние на сопротивление движению; график зависимости 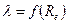
Так как на характер сопротивлений оказывает влияние не только относительная шероховатость, но и форма и распределение выступов по поверхности, то в практику расчетов было введено понятие об эквивалентной равнозернистой шероховатости k э . Под ней понимают такую высоту выступов шероховатости, сложенной из песчинок одинакового размера, которая дает при подсчетах одинаковое с заданной шероховатостью значение коэффициента гидравлического трения 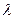
2.11. Потери напора в местных сопротивлениях
Местные потери напора вызываются сопротивлениями в арматуре, фасонных частях и оборудовании, вследствие сужения и расширения потока, изменения направления движения жидкости, слияния и разделения потока и т. п.
Потери на преодоление местных сопротивлений в наружных сетях водопровода обычно не превышают 10-15%, во внутренних сетях – 30% от потерь напора по длине.
Однако местные потери напора в некоторых видах инженерных сетей могут достигать значительной величины: так, например, в системах отопления зданий – до 40%, в воздуховодах вентиляционных систем и пневмотранспорта – до 60-70% от потерь напора по длине.
Местные потери напора определяют как произведение скоростного напора непосредственно вблизи местного сопротивления 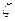
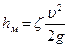
Общей теории для определения коэффициентов местных сопротивлений, за исключением отдельных случаев, нет. Поэтому коэффициенты местных сопротивлений, как правило, находят опытным путем. Значения их для различных элементов трубопроводов приводятся в технических справочниках. Иногда местные сопротивления выражают через эквивалентную длину прямого участка трубопровода 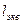
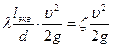
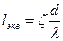
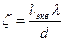
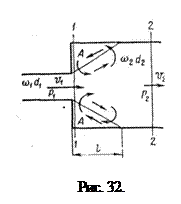
Рассмотрим внезапное расширение трубы с горизонтальной осью. Потеря напора на внезапное расширение равна
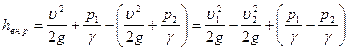
Разность давлений 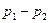
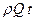
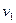
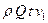
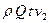
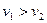
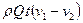
Это изменение количества движения равно импульсу сил давления. Эти силы следующие: в сечении 1-1, где давление 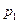
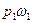
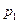
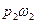
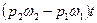
В соответствии с теоремой о количестве движения приравниваем выражения (а) и (б)
Отсюда после деления на 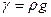
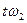
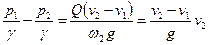
так как 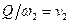
Подставляя правую часть равенства (б) в выражение (а), имеем
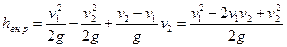
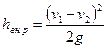
т. е. потери напора при внезапном расширении равны скоростному напору от потерянной скорости. Уравнение (106) называется формулой Борда.
Для выявления значения коэффициента местного сопротивления из уравнения (106) вынесем за скобки

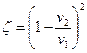
Заменяя скорости через площади живых сечений из уравнения неразрывности 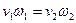
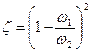
Полученные уравнения (107) и (108) для значения 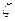
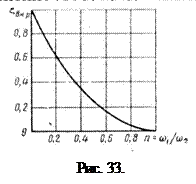
Уравнение (108) представлено в виде графика на рис. 33.
 |
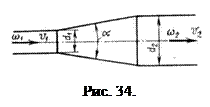
Таким образом, потери напора в диффузоре
равны сумме потерь на расширение и на трение по
длине

Потеря напора на расширение может быть найдена по формуле (106) с введением поправочного коэффициента Ксм , называемого коэффициентом смягчения, который зависит от угла конусности
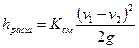
Коэффициент местного сопротивления в этом случае определится по формуле
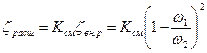
Ксм при 
3) способу подвода воды к рабочему колесу [с односторонним входом воды на рабочее колесо, с двусторонним входом воды (двойного всасывания)];
4) расположению вала (горизонтальные, вертикальные);
5) способу разъема корпуса (с горизонтальным разъемом корпуса, с вертикальным разъемом корпуса);
6) способу отвода жидкости из рабочего колеса в спиральный канал корпуса (спиральные и турбинные). В спиральных насосах жидкость отводится непосредственно в спиральный канал; в турбинных жидкость, прежде чем попасть в спиральный канал, проходит через специальное устройство – направляющий аппарат (неподвижное колесо с лопатками);
7) степени быстроходности рабочего колеса (тихоходные, нормальные, быстроходные);
8) роду перекачиваемой жидкости (водопроводные, канализационные, кислотные и щелочные, нефтяные, землесосные и др.);
9) способу соединения с двигателем [приводные (с редуктором или со шкивом), непосредственного соединения с электродвигателем с помощью муфт]. Насосы со шкивным приводом встречаются в настоящее время редко.
4.3. Теоретическая производительность
Впервые основное уравнение центробежных насосов было выведено членом Петербургской академии наук знаменитым математиком и механиком Л. Эйлером.
В центробежных насосах жидкость подводится к лопаткам рабочего колеса вдоль оси вала (рис. 48). При входе на лопатки происходит отклонение струй от осевого направления к радиальному. Жидкость на лопатки поступает с абсолютной скоростью 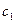
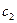
 |
Частицы жидкости между лопатками рабочего колеса совершают сложное движение. Во-первых, они участвуют во вращении с окружной переносной скоростью 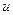
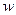
Для упрощения принимают, что движение жидкости является струйным, и траектории движения каждой частицы повторяют очертания лопаток. Такое движение возможно было бы при бесконечно большом числе лопаток.
Абсолютная скорость движения жидкости равна геометрической сумме переносной (окружной) и относительной скоростей (параллелограмм скоростей на рис. 48)
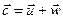
Следует заметить, что окружная скорость 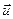
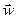
Радиальная составляющая абсолютной скорости на ободе рабочего колеса равна
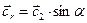
а окружная составляющая
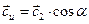
где 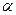
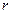
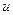
Индексы «1» и «2» приняты для обозначения величин соответственно на входе в рабочее колесо и на выходе из него.
Окружная скорость рабочего колеса на выходе
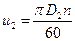
где 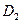
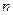
Радиальную составляющую абсолютной скорости можно определить исходя из уравнения неразрывности потока
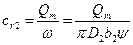
где 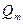
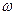
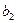
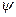
Аналогично можно определить величины абсолютной скорости, окружной скорости, угол между направлением относительной скорости и касательной на входе в рабочее колесо. Абсолютная скорость на входе зависит от конструктивных особенностей рабочего колеса; для большинства насосов угол входа при оптимальном режиме назначается равным 90° с таким расчетом, чтобы избежать гидравлического удара; тогда окружная скорость на входе 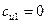
Коэффициент стеснения струи на входе по лабораторным исследованиям можно принять для малых насосов равным 0,75, для больших – 0,83.
В целях предотвращения гидравлического удара при поступлении жидкости на рабочее колесо необходимо, чтобы скорость ее не изменялась ни по величине, ни по направлению, т. е. направление относительной скорости при входе должно совпадать с направлением изгиба тела лопатки. Практика и опыт показывают, что при небольшом отклонении угла до 7-8° поток от лопаток не отрывается и поэтому гидравлические потери на удар можно принимать равными нулю. А это позволяет лопатки рабочего колеса у входа выполнять несколько круче, чем из условия безударного входа. Кроме того, входную кромку лопаток округляют.
После рассмотрения предварительных данных можно перейти к выводу основного уравнения центробежного насоса.
Выше было принято, что рабочее колесо имеет бесконечно большое число лопаток, и работа происходит без гидравлических потерь; это позволяет считать, что весь поток в колесе состоит из одинаковых элементарных струек, имеющих форму межлопаточного пространства колеса, и что скорости во всех точках цилиндрической поверхности данного радиуса одинаковы.
 |
Как известно, работа на перемещение жидкости равна
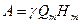
где 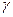
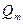
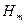
Используем уравнение моментов количества движения, которое для установившегося потока можно сформулировать так: изменение момента количества движения массы жидкости, протекающей в единицу времени при переходе от одного сечения к другому, равно моменту внешних сил, приложенных к потоку между этими сечениями. Относя положение к центробежному насосу, можно отметить, что внешние силы прикладываются к потоку под действием лопаток рабочего колеса. За 1 сек через каналы рабочего колеса протекает объем жидкости, численно равный перекачиваемому секундному расходу 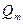

Момент количества движения потока при радиусе 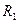
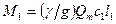
Здесь 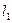
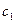
Соответственно, момент количества движения потока у выхода из колеса при радиусе
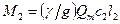
Таким образом, изменение момента количества движения жидкости, протекающей через колесо за 1 сек, равно
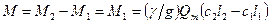
Согласно рис. 49
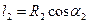
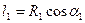
Подставляя эти значения в предыдущее выражение, имеем
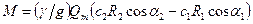
Умножая обе части уравнения на угловую скорость 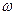
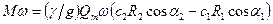
где 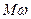
Поток с расходом 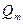

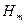
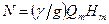
Следовательно, можно записать
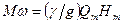
Учитывая, что 
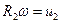
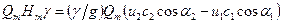
Поделим обе части уравнения на 
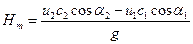
Так как 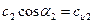

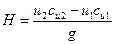
Тангенциальная проекция абсолютной скорости 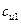
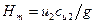
Уравнение (161) показывает, что напор насоса пропорционален окружной скорости (т. е. числу оборотов и диаметру рабочего колеса) и проекции абсолютной скорости 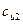
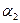
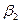
Чтобы учесть конечное число лопаток рабочего колеса и соответственно величину проекции абсолютной скорости на выходе, вводится поправочный коэффициент К. Исходя из изложенного, уравнение для полного напора при конечном числе лопаток можно написать в виде
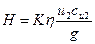
где К – коэффициент, учитывающий конечное число лопаток; 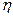
Практически принимают 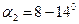
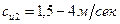

Для определения значения К можно привести одну из формул, полученную академиком Г. Ф. Проскура

где 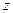
Обычно 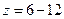
При приближенных расчетах для определения напора в метрах водяного столба (м вод. ст.) можно пользоваться следующим уравнением:
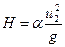
где 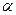
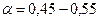
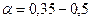

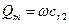
где 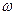
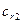
Для центробежных насосов площадь живого сечения рабочего колеса (без учета стеснения его лопатками и утечек через неплотности) определяют как боковую поверхность цилиндра с диаметром, равным внешнему диаметру колеса 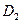
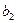
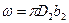
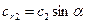
При бесконечно большом числе лопаток радиальная скорость может быть принята одинаковой во всех точках цилиндрической поверхности данного радиуса, а отсюда средняя скорость в уравнении расхода равна радиальной скорости на выходе, т. е. 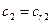
Итак, теоретическая производительность равна:
для выходного сечения
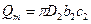
(без учета стеснения и утечек через неплотности);
для входного сечения
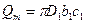
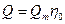
где 
4.4. Характеристики центробежных насосов
Напором насоса Н называется приращение удельной энергии жидкости при движении жидкости через насос. Напор измеряют метрами столба подаваемой жидкости.
ля определения приращения удельной энергии (напора) рассмотрим работу насоса по перекачке жидкости из резервуара А в резервуар Б (рис. 50).
За плоскость сравнения примем свободную поверхность жидкости в резервуаре А, тогда удельная энергия ее при входе в насос определится по формуле
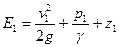
 |
где 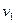
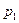
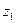
Удельная энергия жидкости при выходе из насоса (в напорном патрубке) равна
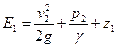
где 
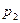
Итак, приращение удельной энергии или полный напор можно определить по формуле
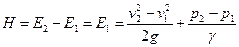
Разрежение на входе в насос измеряется вакуумметром, обычно в кгс/см 2 (или в мм рт. ст). В пересчете на м вод. ст. данной жидкости абсолютное давление на входе в насос равно
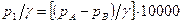
где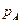
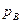
Давление на выходе из насоса 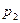
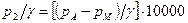
где 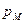

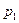
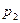
Для воды 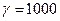
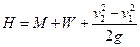
где 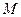
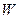
При вычислении полного напора насоса следует учитывать расстояние по вертикали между точкой присоединения вакуумметра и осью стрелки манометра.
Например, для установки, показанной на рис. 51, напор насоса выразится следующим уравнением:

а для установки, показанной на рис. 52,
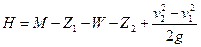
Чтобы определить потребный напор насоса для вновь проектируемой установки, пользуются следующим уравнением:
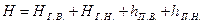

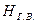
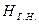
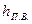

Выше было установлено, что если при входе в рабочее колесо насоса абсолютное давление окажется меньшим или равным упругости паров перекачиваемой жидкости при данной температуре, то жидкость начинает вскипать, происходит разрыв потока и подача прекращается.
При длительной работе насоса в таких условиях разрушается рабочее колесо. Явления, происходящие в насосе при вскипании жидкости, называются кавитацией. При этом из жидкости выделяются пары и растворенные газы в том месте, где давление равно или меньше давления насыщенных паров. Пузырьки пара и газов, увеличенные потоком в область повышенного давления, резко конденсируются с уменьшением объема в микроскопических зонах; это явление, подобное взрывам мельчайших бомб, приводит к механическим повреждениям лопаток колеса и их разрушению. Происходит и химическое разрушение металла в зоне кавитации выделившимся кислородом воздуха (коррозия).
Кавитация может происходить не только в рабочем колесе, но и в направляющем аппарате, и в спиральном корпусе. Эти явления сопровождаются потрескиванием, шумом и вибрацией насоса. При кавитации резко падает к. п. д. насоса, производительность и напор. Особенно сильно при кавитации разрушаются чугун и углеродистая сталь, наиболее устойчивы бронза и нержавеющая сталь. Поэтому в последнее время для изготовления насосов применяют высококачественные материалы и защитные покрытия (наплавка твердых сплавов, поверхностная закалка, металлизация в холодном состоянии), что повышает надежность работы насосов.
Во избежание явления кавитации насос следует располагать как можно ниже.
Кавитационный запас уровня определяют по уравнению
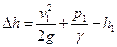
Видео:Закон БернуллиСкачать

Уравнение неразрывности
ГЛАВА III. ГИДРОДИНАМИКА
Основные понятия гидродинамики
Гидродинамика – это раздел гидравлики, в котором изучаются закономерности движения жидкости.
Гидродинамика, или динамика жидкости, существенно отличается от динамики твердого тела. Отдельные частицы твердого тела жестко связаны друг с другом, а в движущейся жидкой среде такие связи отсутствуют, жидкая среда состоит из множества частиц, движущихся одна относительно другой. Законы гидродинамики, определяющие закономерности движения жидкости, сложнее законов покоящейся жидкости. В покоящейся жидкости существует лишь одна характерная величина – гидростатическое давление. При движении состояние жидкости определяется не только давлением, но и величинами и направлением скоростей и ускорений отдельных частиц жидкости. Скорости в данной точке пространства, занятого движущейся жидкостью, являются в общем случае функциями координат этой точки и времени.
Задача гидродинамики – установление связи в движущемся потоке между давлением и кинематическими характеристиками потока. Величины скорости и давления могут изменяться в зависимости от времени и координат рассматриваемой точки.
Введем понятие идеальной жидкости – это такая воображаемая жидкость, которая совершенно лишена вязкости. В такой невязкой идеальной жидкости возможен лишь один вид внутренних напряжений – нормальные напряжения сжатия, т. е. гидромеханическое давление или просто давление. Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости:
· на внешней поверхности жидкости давление направлено по внутренней нормали;
· в любой точке внутри жидкости давление по всем направлениям одинаково.
При рассмотрении движения жидкости различают установившееся и неустановившееся движение.
Если скорость и давление зависят только от координат, т. е. в любой точке потока несжимаемой жидкости эти величины с течением времени остаются неизменными, то такое движение называется установившимся. При установившемся движении скорость и давление являются функцией только координат точки:
Пример установившегося движения – течение воды по трубопроводу при постоянном напоре.
Если давление и скорость в потоке зависят не только от координат, но и от времени, т. е.
то такое движение называется неустановившимся.
Примерами неустановившегося движения могут быть – разгон или торможение жидкости в трубах при включении (выключении) насосов, истечение воды при опорожнении резервуара через отверстие и т. п.
Установившееся движение бывает равномерныминеравномерным.
Равномерным называется движение, при котором скорости жидкости не меняются и с течением времени, и по длине потока, т. е. в сходственных точках поперечных сечений скорости одинаковы по всей длине потока.
Если при движении скорости жидкости, не изменяясь во времени, меняются по длине потока, то такое установившееся движение называется неравномерным. Такой характер движения бывает при сужении или расширении потока в реке, на повороте, в конфузорах и диффузорах.
Напорным называется такое движение, при котором поток со всех сторон ограничен твердыми, жесткими направляющими стенками. Обычно это – движение жидкости в трубах при полном их заполнении (водопроводы, нефтепроводы). Такое движение происходит за счет избыточного давления, создаваемого насосом или водонапорным баком.
Движение, при котором поток лишь частично ограничен твердыми стенками и имеет свободную поверхность, называется безнапорным. Например, течение в реках, водосливных лотках, канализационных трубах. Давление на свободной поверхности обычно равно атмосферному. Движение в таких потоках происходит за счет геометрического уклона русла, т. е. под действием силы тяжести.
Введем еще некоторые определения.
Совокупность или геометрическое место точек, через которые последовательно проходит жидкая частица при своем движении, называется траекторией частицы.
При установившемся движении траектории частиц жидкости являются неизменными во времени.
При неустановившемся течении траектории различных частиц, проходящих через данную точку пространства, могут иметь разную форму.
Линия тока–это линия, касательная к которой в любой точке совпадает с направлением вектора скорости частиц жидкости в данный момент времени (рис. 3.1).
При установившемся течении линия тока совпадает с траекторией частицы жидкости и не меняет своей формы во времени.
Если в движущейся жидкости взять малый замкнутый контур и через все его точки провести линии тока, то образуется трубчатая поверхность, называемая трубкой тока. Если уменьшать размеры замкнутого контура, то часть потока, заключенная внутри трубки тока станет элементарной струйкой, т. е. такой струйкой, в поперечном сечении которой скорости можно считать одинаковыми – рис. 3.2.
При установившемся движении:
· элементарная струйка не меняет своей формы и ориентации в пространстве;
· нормальные составляющие скорости на линии тока равны нулю, следовательно, перетекания жидкости через боковую поверхность данной струйки нет, и трубку тока можно рассматривать как жесткую трубку с непроницаемыми стенками;
· нормальные сечения струйки dS1, dS2 (рис. 3.2) малы, но не одинаковы в разных сечениях, поэтому пучок линий тока внутри трубки может сгущаться и расширяться;
· так как поперечные сечения струйки малы, скорости во всех точках таких сечений можно считать одинаковыми, однако при переходе от одного сечения к другому они изменяются.
При дальнейшем стремлении поперечных размеров струйки к нулю она в пределе стягивается в линию тока.
Перетекания жидкости из одной струйки тока в другую нет, элементарная струйка представляет собой самостоятельный элементарный поток. Таким образом, жидкость втекает во входное отверстие струйки тока и вытекает через выходное, не проникая через ее боковые поверхности. Потоки конечных размеров можно рассматривать как совокупность элементарных струек, т. е. предполагать течение струйным. Из-за различия скоростей струйки будут как бы скользить одна по другой, но перемешиваться не будут.
Введение таких представлений дает возможность использовать для элементарной струйки математический аппарат дифференциального исчисления и интегрирования по всему сечению потока для получения уравнений и закономерностей движения жидкости.
Движение жидкости, при котором линии тока являются строго параллельными прямыми, будем называть параллельноструйным. На практике часто встречаются течения, отличные от параллельноструйных.
Плавно изменяющееся движение – это движение, близкое к параллельноструйному, при котором радиус кривизны линий тока достаточно велик, а угол, образованный крайними линиями тока рассматриваемого потока (или элементарной струйки), близок к нулю (угол θ, рис. 3.3).
Назовем живым сечением потока поверхность, проведенную перпендикулярно линиям тока и находящуюся внутри потока. Поскольку распределение скоростей в потоках в общем случае неравномерно, линии тока в них не параллельны друг другу и живые сечения представляют собой криволинейные поверхности. Например, при движении жидкости в конически расходящейся трубе (рис. 3.4), когда поток состоит из расходящихся элементарных струек, живое сечение представляет собой криволинейную поверхность ABC. Если линии тока в потоке будут параллельными (течение параллельноструйное), живое сечение будет плоским.
Живое сечение может быть ограничено твердыми стенками полностью или частично.
Величина живого сечения определяется его площадью. Однако условия течения жидкости зависят не только от площади живого сечения, но и от его формы. На рис. 3.5 представлены поперечные сечения двух каналов. Хотя живые сечения обоих каналов представляют собой прямоугольники с равновеликими площадями, очевидно, что условия движения жидкости по ним будут разными из-за неодинакового отношения глубины к ширине потока.
Длина линии поперечного сечения, по которой жидкость соприкасается с твердой границей потока, называется смоченным периметром. При напорном течении жидкости, когда поток со всех сторон ограничен твердыми стенками, смоченный периметр будет равен полному периметру живого сечения. В случае безнапорного течения часть периметра поперечного сечения потока, приходящаяся на свободную поверхность жидкости, не включается в расчет смоченного периметра.
Для трубы радиуса r, полностью заполненной жидкостью, смоченный периметр равен (рис. 3.6.а)

В случае безнапорного течения в канале прямоугольного поперечного сечения (рис. 3.6.б)
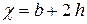
Отношение площади сечения потока жидкости ω к смоченному периметру 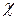
Для напорного потока в круглой трубе (рис. 3.6.а)
Для безнапорного потока (рис. 3.6.б)
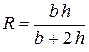
Из этой формулы понятно, что гидравлический радиус канала а на рис. 3.5 больше гидравлического радиуса канала б.
a  | б 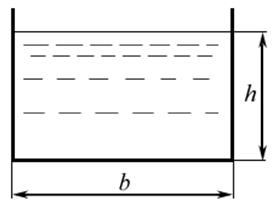 |
| Рис. 3.6 |
Расходом называют количество жидкости (в объемных или весовых единицах), протекающее через поперечное (живое) сечение потока в единицу времени. В зависимости от того, в каких единицах определяется количество жидкости, различают объемный Q, весовой Qв и массовый Qм расходы. Зависимость между ними следующая
где V – количество (объем) жидкости;
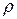
g – ускорение свободного падения.
В гидравлике чаще всего используют объемный расход, далее под термином «расход» будем понимать именно объемный расход, если специально не оговорим иное.
Рассмотрим движение жидкости на участке элементарной струйки (рис. 3.7). Частичка жидкости перемещается от сечения 1 к сечению 2 за промежуток времени dt, проходя при этом расстояние l. Поскольку стенки трубки тока непроницаемы для движущейся жидкости, количество жидкости, прошедшее через сечение 1 за время dt будет равным объему цилиндра:

где dω – площадь живого сечения струйки.
Элементарный объемный расход, т. е. количество жидкости, прохо-дящее в единицу времени через живое сечение элементарной струйки, определится как
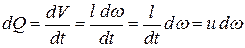
Если рассматривать поток жидкости как совокупность элементарных струек, то общий расход потока определится как сумма элементарных расходов отдельных струек:
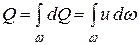
Чтобы вычислить расход по этой формуле, нужно знать распределение скорости движения жидкости во всех точках живого сечения (рис. 3.8). Чтобы упростить расчеты для практического применения, вводится понятие средней скорости потока.
Средняя скорость в сечении 
Тогда уравнение расхода для полного потока запишется как
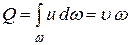
где: 
Среднюю скорость тогда можно определить как

Средняя скорость по живому сечению – абстрактное понятие, введенное для упрощения изучения движения жидкости.
Уравнение неразрывности
Уравнение неразрывности как для элементарной струйки, так и для всего потока – это математическое выражение условия сплошности потока при установившемся течении жидкости.
Выделим в потоке элементарную струйку (рис. 3.9).
Рассмотрим участок между сечениями 1–1 и 2–2. За время dt внутрь этого участка через сечение 1–1 войдет количество жидкости, равное объему цилиндра с площадью основания dS1 и образующей u1dt. Через сечение 2–2 за это же время вытечет объем жидкости, равный 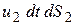
· через боковые поверхности элементарной струйки жидкость не проникает (таково свойство трубки тока);
· жидкость несжимаема и в ней отсутствуют пустоты и разрывы.
Это означает, что будет справедливым равенство

 . . | (3.1) |
Для других сечений будут справедливы такие же соотношения:
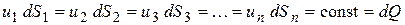
Это уравнение (3.1) и выражает условие неразрывности элементарной струйки, из него следует, что через все сечения струйки проходит одинаковый расход жидкости. Из уравнения понятно, что
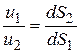
т. е. скорости течения в разных сечениях элементарной струйки обратно пропорциональны площадям этих сечений.
Для полного потока уравнение неразрывности можно получить, проинтегрировав уравнение (3.1) по площадям соответствующих сечений полного потока (рис. 3.9):

Используя понятие средней скорости по сечению
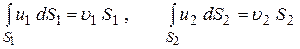
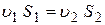 . . | (3.2) |
Так как сечения 1–1 и 2–2 выбраны произвольно, то и для любых других сечений это равенство будет справедливо.
 . . | (3.3) |
Уравнения (3.2) и (3.3) и есть уравнения неразрывности полного потока. Они показывают, что объемный расход несжимаемой жидкости при установившемся движении остается постоянным вдоль всего потока.
Из уравнения (3.2) следует, что средние скорости потока обратно пропорциональны площадям соответствующих живых сечений:
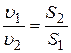
📽️ Видео
Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Вывод уравнения неразрывности - Лекция 1Скачать

Физика. 10 класс. Уравнение неразрывности. Уравнение Бернулли. Подъёмная сила /29.10.2020/Скачать

Лекция 2. Уравнение неразрывностиСкачать

Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Уравнение Бернулли и его приложения | Гидродинамика, ГидравликаСкачать

Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Теорема Эйлера о движении жидкостиСкачать

Математический анализ, 5 урок, Непрерывность функцииСкачать

Уравнение БернуллиСкачать

Урок 134. Применения уравнения Бернулли (ч.1)Скачать

РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

Уравнение Бернулли | ДиффурыСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Уравнение БернуллиСкачать







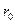 сила взаимодействия равна нулю, то есть силы отталкивания уравновешивают силы притяжения. При
сила взаимодействия равна нулю, то есть силы отталкивания уравновешивают силы притяжения. При 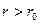 результирующей силой является сила притяжения, которая растет по абсолютной величине, достигая максимума при
результирующей силой является сила притяжения, которая растет по абсолютной величине, достигая максимума при 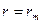 , а затем уменьшается. При
, а затем уменьшается. При 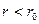 – силы отталкивания. Молекула в поле этих сил обладает потенциальной энергией
– силы отталкивания. Молекула в поле этих сил обладает потенциальной энергией 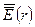 , которая связана с силой f ( r ) дифференциальным соотношением
, которая связана с силой f ( r ) дифференциальным соотношением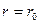 ,
, 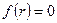 ,
, 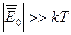 (2)
(2)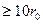 , что соответствует слабым силам притяжения и малой потенциальной энергии. Тепловое движение доминирует над силами притяжения
, что соответствует слабым силам притяжения и малой потенциальной энергии. Тепловое движение доминирует над силами притяжения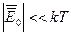 (3)
(3)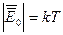 (4)
(4)