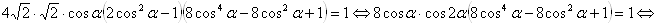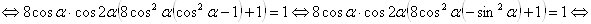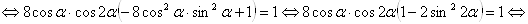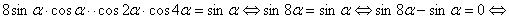Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.). Как известно, рациональные уравнения изучаются в 8-9 классах. Стандарт образования ставит целью формирование умения решать простейшие целые, дробно-рациональные уравнения и применять их на практике. Дробно-рациональные уравнения в дальнейшем широко используются при решении логарифмических, показательных, иррациональных уравнений и неравенств, часто встречаются в задачах повышенной трудности, в заданиях математических олимпиад, в вариантах выпускных и вступительных экзаменационных работ в вузы.
- Скачать:
- Предварительный просмотр:
- Предварительный просмотр:
- Подписи к слайдам:
- Реферат по математике. «Методы решения рациональных уравнений». — презентация
- Похожие презентации
- Презентация на тему: » Реферат по математике. «Методы решения рациональных уравнений».» — Транскрипт:
- Рациональные уравнения
- 📸 Видео
Видео:РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ. §7 алгебра 8 классСкачать

Скачать:
| Вложение | Размер |
|---|---|
| ratsionalnye_uravneniya_v_kurse_algebry_osnovnoy_shkoly.docx | 2.77 МБ |
| zashchita.pptx | 2.22 МБ |
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Предварительный просмотр:
Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Подписи к слайдам:
«РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ В КУРСЕ АЛГЕБРЫ ОСНОВНОЙ ШКОЛЫ » Подготовила: Горобцова Елена Васильевна Научный руководитель: кандидат педагогических наук, доцент кафедры информатики и МПМ Титоренко Светлана Алексеевна
выделить основные методы решения рациональных уравнений и разработать соответствующую систему упражнений. ЦелЬ исследования:
курс математики основной школы. Объект исследования:
рациональные уравнения в курсе математики основной школы. Предмет ИСЛЕДОВАНИЯ:
Задачи: Изучить литературу по теме исследования. Дать определения основным понятиям темы „Рациональные уравнения”. Выделить основные методы решения данных уравнений. Разработать систему упражнений, в которой должны быть представлены как основные виды рациональных уравнений, так и методы их решения. Показать особенности решения разных видов рациональных уравнений.
Введение Глава 1. Классификация уравнений. Методы решения рациональных уравнений Краткие исторические сведения Основные понятия линий уравнений Классификация уравнений. Рациональные уравнения Методы решения рациональных уравнений Глава 2. Система упражнений по теме «Рациональные уравнения » Примеры уравнений, сводимых к квадратным Примеры уравнений, решаемых методом замены переменной Примеры уравнений, решаемых графическим методом Примеры уравнений с модулем, решаемых с применением метода интервало в С одержание :
Глава 3. Методические рекомендации по изучению данной темы в школьном курсе математики Общие методические рекомендации Разработка урока по теме «Линейные уравнения» Разработка урока по теме «Квадратные уравнения» Разработка урока по теме «Дробно – рациональные уравнения» Заключение Список используемой литературы С одержание :
Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Реферат по математике. «Методы решения рациональных уравнений». — презентация
Презентация была опубликована 8 лет назад пользователемАльбина Ларионова
Похожие презентации
Видео:Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

Презентация на тему: » Реферат по математике. «Методы решения рациональных уравнений».» — Транскрипт:
1 Реферат по математике. «Методы решения рациональных уравнений».
2 Введение. Целью написания этого реферата является ознакомление с различными, основанными на материале программы общеобразовательной средней школы методами решения уравнений, иллюстрирование широких возможностей использования хорошо усвоенных школьных знаний, закрепление и систематизация навыков решения рациональных уравнений.
3 Рациональные уравнения. Функция вида P(x) = a 0 x n + a 1 x n – 1 + a 2 x n – 2 + … + a n – 1 x + a n, где n натуральное, a 0, a 1,…, a n некоторые действительные числа, называется целой рациональной функцией.
4 Возвратные уравнения. Уравнение вида a n x n +a n–1 x n–1 +…+a 1 x+a 0 =0 Уравнение вида a n x n +a n–1 x n–1 +…+a 1 x+a 0 =0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, то есть если a n – 1 = a k, при k = 0, 1, …, n.
5 Пример. Решить уравнение: 2х 4 +3х 3 -3х 2 -3х+2=0 Решение. Так как х=0 не является корнем этого уравнения, то оно равносильно уравнению 2х 2 +3х-3-3/х+2/х 2 =0. 2(х 2 +1/х 2 )+3(х-1/х)-3=0. Пусть х-(1/х)=у. Получаем: 2у 2 +3у+1=0. Корни этого уравнения есть у 1 =-1 и у 2 =-0, 5. Возвратные уравнения.
6 Исходное уравнение равносильно совокупности уравнений х-(1/х)=-1 и х-(1/х)=-0,5 Решения первого уравнения этой совокупности есть х 1 =-0,5(1+ 5) и х 2 =-0,5(1- 5), а решения второго х 3 =-0,25(1- 17) и х 4 =-0,25(1+ 17). Следовательно, эти четыре корня являются корнями исходного уравнения. Ответ: х 1 =-0,5(1+ 5), х 2 =-0,5(1- 5), х 3 = -0,25(1+ 17), х 4 =-0,25(1- 17). Возвратные уравнения.
7 Решение симметрических систем уравнений. Многочлен P(x,y) называется симметрическим, если P (x,y)=P(y,x). При решении систем уравнений вида P 1 (x,y)=0, P 2 (x,y)=0,где P 1 (x,y) и P 2 (x,y) симметрические многочлены, полезной оказывается такая замена неизвестных: x+y=U, xy=V. Любой симметрический многочлен P(x, y) можно представить как выражение от U и V. P 2 (x,y)=0,где P 1 (x,y) и P 2 (x,y) симметрические многочлены, полезной оказывается такая замена неизвестных: x+y=U, xy=V. Любой симметрический многочлен P(x, y) можно представить как выражение от U и V.
8 Пример. Решить систему уравнений x 2 + xy + y 2 = 49, x + y + xy = 23. Решение. x 2 +xy+y 2 =x 2 +2xy+y 2 xy=(x+y) 2 xy. Сделаем замену неизвестных: x+y=U, xy=V. Система примет вид: U 2 V=49, U+V=23. Решение симметрических систем уравнений. систем уравнений.
9 Сложив эти уравнения, получим уравнение U 2 + U 72 = 0 с корнями U 1 = 8,U 2 = 9. Соответственно V 1 =15, V 2 = 32. Остаётся решить системы уравнений: x + y = 8, xy = 15, xy = 15, x + y = 9, x + y = 9, xy = 32. xy = 32. Решение симметрических систем уравнений.
10 Система x+y=8, xy = 15. xy = 15. имеет решения: x 1 =3,y 1 =5;x 2 =5, y 2 =3. Система x+y= 9, xy=32. xy=32. действительных решений не имеет. Ответ: x 1 = 3, y 1 = 5; x 2 = 5, y 2 = 3. Решение симметрических систем уравнений. систем уравнений.
11 Уравнения и системы уравнений с параметрами. Иногда в уравнениях некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами. Такие буквы называются параметрами. Предполагается, что эти параметры могут принимать любые числовые значения, т.е. одно уравнения с параметрами задаёт множество уравнений (для всех возможных значений параметров). Иногда в уравнениях некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами. Такие буквы называются параметрами. Предполагается, что эти параметры могут принимать любые числовые значения, т.е. одно уравнения с параметрами задаёт множество уравнений (для всех возможных значений параметров).
12 Решить уравнение с параметрами означает следующее: исследовать, при каких значениях параметров уравнение имеет корни и сколько их при разных значениях параметров. найти все выражения для корней и указать для каждого из них те значения параметров, при которых это выражение действительно определяет корень уравнения. Уравнения и системы уравнений с параметрами.
13 Пример. Решим уравнение px=6 с неизвестным x и параметром p. Если p 0, то можно разделить обе части уравнения на p, и тогда мы находим корень уравнения x=6/p. Если p=0, то уравнение корней не имеет, потому что 0 x=0 для любого x. Ответ: при p 0 уравнение имеет единственный корень x=6/p; при p=0 уравнение корней не имеет. Уравнения и системы уравнений с параметрами.
14 Графический метод решения систем нелинейных уравнений. Системы нелинейных уравнений с двумя неизвестными можно решать графически. Для этого нужно начертить графики обоих уравнений и найти координаты точек их пересечения.
15 Графический метод решения систем нелинейных уравнений. Пример. Найдём графически корни системы: x 2 + y 2 2x + 4y 20 = 0, 2x y = 1. Решение. Выделяя полные квадраты, получаем: x 2 + y 2 2x + 4y 20 = (x 2 2x +1) + (y 2 + 4y + 4) = (x 1) 2 + (y + 2) Значит, систему уравнений можно записать так: (x 1) 2 + (y + 2) 2 = 25, 2x y = 1.
16 Графический метод решения систем нелинейных уравнений. Графиком первого уравнения является окружность с центром A(1; 2) и радиусом 5. А 2x y = 1 уравнение прямой, проходящей через точки B(0; 1) и C(2; 5). Строим окружность радиуса 5 с центром в точке A и проводим прямую через точки B и C. Эти линии пересекаются в двух точках M(1; 3) и N( 3; 5). Значит решение системы таково: x 1 = 1, y 1 = 3; x 2 = 3, y 2 = 5. A 2 N 02 X Y B C5 M
17 Заключение Таким образом, рассмотрев всевозможные методы решения рациональных уравнений, можно выделить основные: Таким образом, рассмотрев всевозможные методы решения рациональных уравнений, можно выделить основные: 1)Простейшие: решаются путём обычных упрощений приведение к общему знаменателю, приведение подобных членов и так далее. Квадратные уравнения ax 2 +bx+c=0 решаются по выведенной нами формуле
18 Заключение 2) Группировка: путём группировки слагаемых, применения формул сокращённого умножения привести (если удастся) уравнение к виду, когда слева записано произведение нескольких сомножителей, а справа ноль. Затем приравниваем к нулю каждый из сомножителей.
19 Заключение 3) Подстановка: ищем в уравнении некоторое повторяющееся выражение, которое обозначим новой переменной, тем самым упрощая вид уравнения.
20 Заключение 4) Подбор: при решении уравнений высших степеней рациональные корни уравнения a n x n +a n – 1 x n– 1 +…+a 1 x+a 0 =0 ищем в виде p/q, где pделитель a 0, qделитель a n,p и q взаимно просты, p Z, q N.
21 Заключение 5) Искусство, т.е. решать пример нестандартно, придумать свой метод, догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д.
22 Заключение 6) Уравнения с модулем: при решении уравнений с модулем используется определение модуля и метод интервалов. Напомним, что f(x) = f(x), если f(x) 0, f(x) =–f(x), если f(x)
Видео:Равносильные уравнения. Рациональные уравнения - 8 класс алгебраСкачать

Рациональные уравнения
1.2 Рациональные уравнения
Тригонометрическая подстановка применяется при решении рациональных уравнений, когда уравнение не имеет рациональных корней или найденные рациональные решения не исчерпывают всего множества решений уравнения.
При решении иррациональных уравнений возможность введения тригонометрической подстановки была видна по структуре уравнения. В нескольких следующих задачах применение метода тригонометрической подстановки не так очевидно. Вот почему прежде чем ввести подстановку, нужно доказать законность такого введения.
Пример 1. Сколько корней имеет уравнение
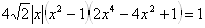
Решение этой задачи любым методом начинается одинаково. Докажем, что все корни данного уравнения принадлежат промежутку 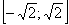
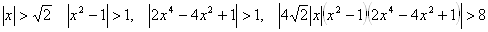
Но тогда в исходном уравнении слева стоит произведение больше восьми, а справа единица, что невозможно.
Решение с помощью тригонометрической подстановки
Положим 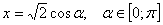
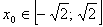
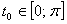
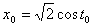
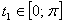
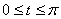
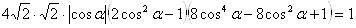
Так как 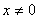
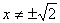
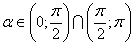
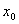
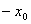
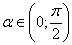
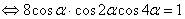
Так как 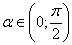
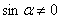
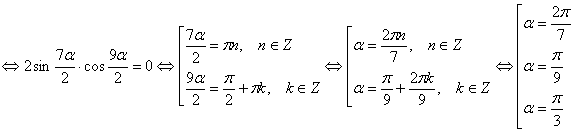
Ответ: шесть корней.
Алгебраическое решение Так как выражение от правой части равенства четное и 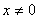
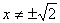
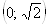
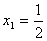
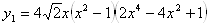
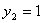
и функция 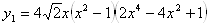
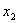
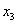
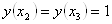
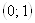
В данном случае можно решать любым способом, но если количество корней на небольшом промежутке достаточно велико, вычисления могут оказаться громоздкими, и сам метод неэффективным. В этом случае на помощь приходит метод тригонометрической подстановки. Надо заметить, что решить вопрос о количестве корней можно с помощью производной, но в данном случае такое решение мало эффективно, так как затруднительно найти нули производной.
Пример 2. Решить уравнение
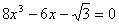
Если для выше приведенных задач не удается найти нетрадиционный путь решения, то все равно остается вероятность справиться с задачей с помощью стандартных школьных рассуждений, правда, затратив при этом гораздо больше времени. Эта задача лишает такого выбора, так как ее решение другим способом не представляется возможным.
Решение с помощью тригонометрической подстановки
Поделим все члены уравнения на 2. Уравнение примет вид
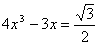
Докажем, что все корни данного уравнения по модулю не превосходят единицы. Пусть 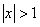
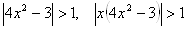
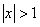
Положим 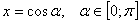
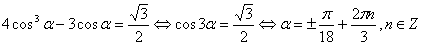
Условию 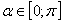
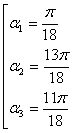
Поскольку кубическое уравнение не может иметь больше трех различных корней, то мы нашли все решения.
Ответ: 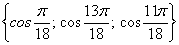
📸 Видео
Решение дробных рациональных уравнений. Алгебра, 8 классСкачать

Рациональные уравнения. ОГЭ номер 21 | ЕГЭ номер 13 | Математика | TutorOnlineСкачать

Рациональные уравнения. Равносильные уравнения. Алгебра 8клСкачать

Дробно-рациональные уравнения. Подготовка к экзаменам. 57 часть. 9 класс.Скачать

#136 Урок 61. Дробно-рациональные уравнения. Рациональные уравнения, приводящиеся к квадратным.Скачать

8 класс, 28 урок, Рациональные уравнения как математические модели реальных ситуацийСкачать

ЭТО НУЖНО ЗНАТЬ — Как решать Дробно Рациональные уравнения?Скачать

ЛУЧШАЯ СТРАТЕГИЯ решения Целых Рациональных Уравнений (математика с нуля)Скачать

Рациональные уравнения/ ОГЭ #311381 тип 9Скачать

Дробно-рациональные уравнения + Бонус: треугольник Паскаля | МатематикаСкачать

Дробно рациональное уравнение. ОГЭ математика задача 4 (тип 4) 🔴Скачать

РАЗБИРАЕМ ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ ЧАСТЬ II #shorts #математика #егэ #огэ #профильныйегэСкачать

Дробно-рациональные уравнения. Подготовка к экзаменам. 64 часть. 9 класс.Скачать

Сложные рациональные уравнения | МатематикаСкачать