Реальный электродный потенциал уравнение нернста

Учение об электродвижущих силах гальванических элементов является одним из основных разделов электрохимии. Начало изучению электродвижущих сил бы­ло положено еще М. В. Ломоносовым (1750), который в своих работах отмечал связь между химическими и электрическими явлениями. Позднее наблюдения итальянского физиолога Гальвани (1780) и обширные работы итальянского физи­ка Вольта (1780) привели к открытию гальванических элементов.

В 1800 г. Вольта изобрел первый химический источник тока, так называемый вольтов столб, который был собран из пластинок различных металлов, разделен­ных прослойками ткани, смоченной электролитом. Исследования привели Вольта к открытию контактной разности потенциалов, возникающей при соприкосновении металлов различной природы. В первых исследованиях в качестве чувствительного прибора для обнаружения малой разности потенциалов ученый использовал свежеанатомированные мышцы лягушки. Этот случай является наглядным примером того, как биологические методы исследования нередко могут способствовать ус­пешному развитию физики и других точных наук.

Открытие химических источников тока и контактной разности потенциалов оказало большое влияние на все последующее развитие электрохимических явле­ний. В настоящее время методы электрохимии получили широкое распростране­ние в агрохимии, физиологии растений, в биологии, почвоведении, а также во мно­гих других смежных дисциплинах.

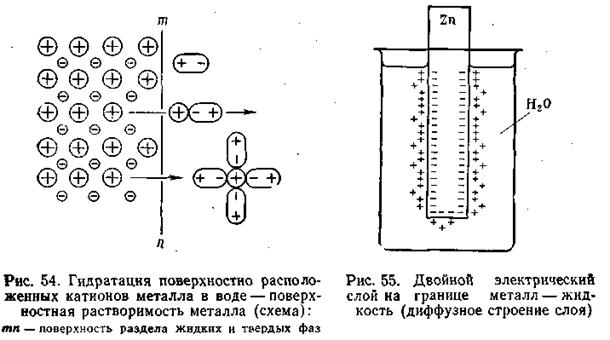
Если в чистую воду погрузить пластинку какого-либо металла, то согласно гидратной теории Д. И. Менделеева ионы металла бу­дут взаимодействовать с полярными молекулами воды. Иными сло­вами, поверхностно расположенные катионы этого металла будут гидратироваться молекулами воды и переходить в окружающий раствор, заряжая его положительно, т. е. металл будет как бы рас­творяться (рис.4.8).

Однако электроны, в избытке остающиеся в металле, заряжают его поверхностный слой отрицательно. В результате этого между ионами металла, перешедшими в раствор, и поверхностью металли­ческой пластинки возникают силы электростатического притяже­ния, в силу чего ионы, окружающие пластинку, образуют так назы­ваемый двойной электрический слой, схема которого приведена на рис. 4.8. Этот слой препятствует дальнейшему растворению металла и в системе устанавливается подвижное равновесие, которое харак­теризуется равными скоростями как растворения, так и обратного осаждения ионов из раствора на поверхности металлической пла­стинки.

Первоначально считали, что двойной электрический слой имеет плоское строение. Он уподоблялся конденсатору, одна из обкладок которого расположена на поверхности металла, другая — в слое прилегающей к электроду жидкости. Расстояние между обкладками равно диаметру молекулы.

Согласно этой теории, которую обычно связывают с именем Гельмгольца (1879), учитывалось только прояв­ление электростатических сил взаимодействия между зарядами про­тивоположного знака и не учитывалось изменение свойств двойного электрического слоя с изменением концентрации электролита и его температуры, что явилось основным недостатком теории Гельм­гольца.

В разработке современной теории строения двойного электриче­ского слоя на границе твердая фаза—жидкость и методов его ис­следования ведущая роль принадлежит А. Н. Фрумкину и его шко­ле. Работы А. Н. Фрумкина и его учеников установили, что слой ионов, располагающийся в жидкости, благодаря действию двух про­тивоположно направленных сил (электростатического притяжения и теплового движения) имеет диффузное строение, т. е. он проника­ет в жидкость на некоторую глубину (рис. 4.8).

Определенная часть ионов удерживается вблизи поверхности раздела металл—электролит, образуя обкладку двойного слоя с толщиной, отвечающей среднему радиусу ионов электролита. Ос­тальные ионы, входящие в состав двойного слоя, распределяются диффузно, с постепенно убывающей плотностью заряда.

Таким образом, при соприкосновении металла с водой ионы его находятся под действием двух конкурирующих сил: электростати­ческого притяжения, возникающего между ионами металла и моле­кулами воды (явление гидратации), и электростатического притя­жения со стороны электронного газа, определяющего прочность кристаллической решетки.

Вполне понятно, что чем прочнее кристаллическая решетка ме­талла, тем труднее иону металла перейти в раствор. Чем выше величина энергии гидратации, тем с большей жадностью молекулы воды взаимодействуют с этими ионами, и тем легче им выделиться в рас­твор.

В результате взаимодействия двух указанных взаимно противо­положных сил растворение металла в воде приобретает характер только поверхностного процесса и охватывает лишь очень узкую об­ласть на границе металл—жидкость. В этом поверхностном слое концентрация ионов металла, несмотря на его чрезвычайно малую растворимость, может быть довольно значительной. Кроме того, в поверхностном растворе гидратированные катионы в силу электро­статических сил притяжения со стороны электронов кристалличе­ской решетки металла совершают лишь ограниченное кинетическое движение в виде так называемых «пристенных» скачков. Они проч­но связаны с жестким каркасом кристаллической решетки металла.

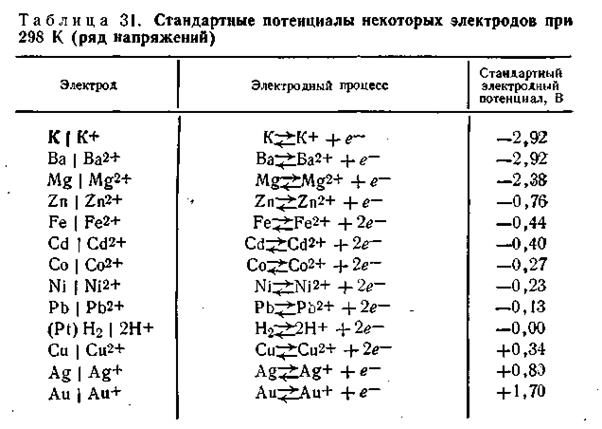
Таким образом, в системе металл — вода на границе раздела фаз возникает двойной электрический слой, блокирующий поверх­ность металла. Образовавшаяся пограничная разность потенциалов получила название электродного потенциала (дат. potentia — воз­можность, мощь).

Если жидкая среда — чистая вода, для всех металлов картина в качественном отношении будет однозначной: металл заряжается от­рицательно, прилегающий слой жидкости — положительно. Однако количественно для разных металлов будут наблюдаться существен­ные различия, что объясняется не только неодинаковой энергией связи катионов этих металлов в кристаллической решетке, но и не­одинаковой гидратируемостью этих катионов.

Несколько иная картина наблюдается в случае, если металличе­скую пластинку погрузить не в чистую воду, а в раствор соли этого металла. При этом могут иметь место три случая.

1. Исходная концентрация ионов данного металла в растворе С меньше концентрации С_о, соответствующей равновесному состоянию ионов после погружения в раствор металлической пластинки, т. е. С С₀. В этом случае наблюдается обратное явле­ние: ионы металла из раствора выделяются на поверхности метал­лической пластинки. Чтобы ионы металла могли выделиться, они должны присоединить электроны согласно уравнению (б). Посколь­ку источника электронов в системе нет, выделение металла на поверхности пластинки происходит в виде ионов. В результате поверх­ность приобретает положительный заряд.

3. При условии С=С₀ вся система будет находиться в состоянии подвижного равновесия, разность потенциалов между жидкостью и металлом равна нулю. В этом случае из раствора осаждается на единицу поверхности металла столько же катионов, сколько их вы­ходит в двойной электрический слой.

Принимая это во внимание, нетрудно найти математическую за­висимость между величиной скачка потенциала на границе сопри­косновения металла и раствора и концентрацией (точнее, актив­ностью) ионов этого металла в растворе.

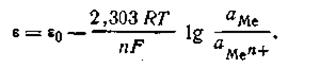4.84

Так как активность металла принимается равной единице (а_Mе= 1), то с учетом этого уравнения (4.84) будет иметь следующее выражение:

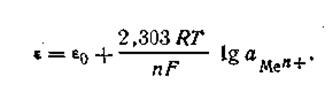4.85

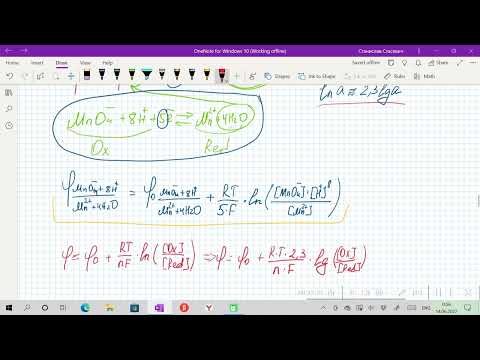
Уравнение (4.85) называется уравнением Нернста,

ε₀— постоянная величина, характеризующая электрохимическую природу электрода.

Для расчетов удобнее предварительно вычислить значение R·T· 2,303/F при какой-либо температуре. Например, при 291 К это число будет равно 0,0577. Следовательно, для температуры 291 К уравнение Нернста будет иметь вид:

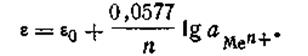4.86

Обозначим численное значение выражения R·T·2,303/F буквой Ж.

Зависимость этого числа от температуры выразится следующей формулой:

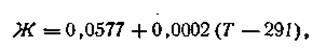4.87

где Г —любая температура, при которой производится измерение разности потенциалов. С учетом этого обозначения уравнение элек­тродного потенциала Нернста будет иметь следующий вид:

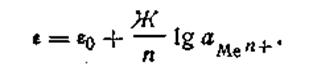4.88

Каков же физический смысл ε_о в уравнении электродного потен­циала Нернста? Несложный математический анализ этого уравне­ния показывает, что при С=1 моль/л все выражение

обращается в нуль, и тогда

4.89

Таким образом, стандартным (нормальным) потенциалом назы­вается такой потенциал, который возникает на металлической плас­тинке, находящейся в контакте с одноименными ионами в растворе, с концентрацией С=1 моль/л.

За нулевую точку измерения потенциалов условно принят нор­мальный потенциал водородного электрода. Для изготовления его используют способность платины растворять га­зообразный водород. Платиновая проволока или пластинка, содер­жащая растворенный водород, играет роль «водородной пластинки», а функции «раствора солей» может выполнять любой водный раствор, в котором всегда присутствуют ионы водорода Н + . Причем нормальный потенциал водородного электрода равен нулю при ус­ловии, что давление молекулярного водорода на пластинке равно 101,325 кПа и С_Н+ = 1 моль/л.

Если нормальный потенциал какого-либо металла больше во­дородного, его принято считать положительным, если меньше — от­рицательном.

Если все металлы расположить последовательно по возраста­ющей величине их нормальных электродных потенциалов, получит­ся ряд напряжений. В табл. 4.9 приведены стандартные потенциалы некоторых металлов.

В этой таблице каждый электрод обозначен символом элемента, из которого он состоит, и соответствующего иона, а вертикальная линейка изображает поверхность раздела двух фаз, где имеет место скачок потенциала.

Представленным в табл. 4.9 рядом напряжений широко пользу­ются в практике при составлении так называемых гальванических элементов, а также при изучении взаимодействия между металлами и кислотами, между солями и металлами. Зная ряд напряжений, можно предвидеть направление реакции вытеснения одних элемен­тов другими. Так металлы, стоящие в ряду напряжений после водо­рода, не способны вытеснять водород из кислот. Вытеснение метал­ла из солей другим металлом осуществляется только в том случае, если вытесняющий металл расположен в ряду напряжений до вытес­няемого.

Например, при составлении гальванического элемента из цинка и свинца в качестве положительного электрода следует взять свин­цовый (ε_о= -0,13 В), а в качестве отрицательного — цинковый (ε_о= -0,76 В).

Электроды подразделяются на электроды первого и второго ро­да. Электроды первого рода — это электроды из металла, погружен­ного в раствор, содержащий ионы того же металла (например, Cu|Cu 2+ , Zn|Zn 2+ ). Эти электроды обратимо обменивают катионы Ме↔Ме n + nе, где n — число теряемых (или приобретаемых) электронов (е — ).

Электроды второго рода состоят из металла, покрытого слоем труднорастворимой соли и погруженного в раствор какой-либо лег­корастворимой соли с тем же анионом. Такие электроды обратимы относительно этого аниона.

Для электродов второго рода выражение электродного потенциала

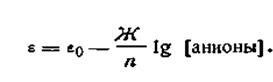4.90

Дата добавления: 2016-02-20 ; просмотров: 2592 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Уравнение НернстаСкачать

Применение уравнения Нернста в решении задач.

При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:

Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:

Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.

Пример 1:

Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO₄ и 0.01М ZnSO₄ соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.

Решение:

Для начала запишем уравнения протекающих процессов:

Далее находим по таблице стандартные потенциалы процессов:

Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.

Найдем реальные потенциалы с учетом нестандартных активностей ионов:

Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:

Ответ: 1.13 В

Пример 2:

Одним из лабораторных способов получения хлора является действие KMnO₄ на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?

Решение:

Для начала запишем уравнения протекающих процессов.

Далее находим по таблице стандартные потенциалы процессов:

Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи:

Получается, что потенциал KMnO₄ стал меньше, чем у хлора, а значит, реакция не пойдет.

Видео:Уравнение Нернста. Условия изменения направления ОВР. Продукты в ОВР. Ч.5-3.Скачать

Окислительно — восстановительный потенциал

Видео:Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать

Электродные потенциалы. ЭДС реакции

Окислительно — восстановительный потенциал является частным, узким случаем понятия электродного потенциала. Рассмотрим подробнее эти понятия.

В ОВР передача электронов восстановителями окислителям происходит при непосредственном контакте частиц, и энергия химической реакции переходит в теплоту.

Энергия любой ОВР, протекающей в растворе электролита, может быть превращена в электрическую энергию, если, например, окислительно-восстановительные процессы разделить пространственно, т.е. передача электронов восстановителем будет происходить через проводник электричества.

Это реализовано в гальванических элементах, где электрическая энергия получается из химической энергии окислительно-восстановительной реакции.

Видео:4 3 Электрохимический потенциалСкачать

Элемент Даниэля-Якоби

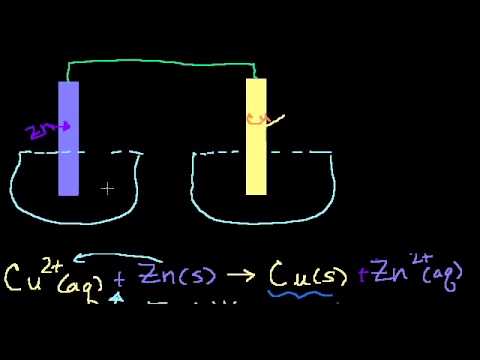
Рассмотрим гальванический элемент Даниэля-Якоби, в котором левый сосуд наполнен раствором сульфата цинка ZnSO₄, с опущенной в него цинковой пластинкой, а правый сосуд – раствором сульфата меди CuSO₄, с опущенным в него медной пластинкой.

Взаимодействие между раствором и пластиной, которая выступает в качестве электрода, способствует тому, чтобы электрод приобрел электрический заряд.

Возникающая на границе металл-раствор электролита разность потенциалов, называется электродным потенциалом. Значение и знак (+ или -) электродного потенциала определяются природой раствора и находящегося в нем металла.

При погружении металлов в растворы их солей более активные из них (Zn, Fe и др.) заряжаются отрицательно, а менее активные (Cu, Ag, Au и др.) положительно.

Результатом соединения цинковой и медной пластинки проводником электричества, является возникновение в цепи электрического тока за счет перетекания электронов с цинковой к медной пластинке по проводнику.

При этом происходит уменьшение количества электронов в цинке, что компенсируется переходом Zn 2+ в раствор т.е. происходит растворение цинкового электрода — анода (процесс окисления).

Zn — 2e — = Zn 2+

В свою очередь, рост количества электронов в меди компенсируется разряжением ионов меди, содержащихся в растворе, что приводит к накоплению меди на медном электроде – катоде (процесс восстановления):

Cu 2+ + 2e — = Cu

Таким образом, в элементе Даниэля-Якоби происходит такая реакция:

Zn + Cu 2+ = Zn 2+ + Cu

Zn + CuSO₄ = ZnSO₄ + Cu

Количественно охарактеризовать окислительно-восстановительные процессы позволяют электродные потенциалы, измеренные относительно нормального водородного электрода (его потенциал принят равным нулю).

Чтобы определить стандартные электродные потенциалы используют элемент, одним из электродов которого является испытуемый металл (или неметалл), а другим является водородный электрод. По найденной разности потенциалов на полюсах элемента определяют нормальный потенциал исследуемого металла.

Видео:011 Электрохимия 4 уравнение НернстаСкачать

Окислительно-восстановительный потенциал

Значениями окислительно-восстановительного потенциала пользуются в случае необходимости определения направления протекания реакции в водных или других растворах.

2Fe 3+ + 2I — = 2Fe 2+ + I₂

таким образом, чтобы йодид-ионы и ионы железа обменивались своими электронами через проводник.

В сосуды, содержащие растворы Fe 3+ и I — , поместим инертные (платиновые или угольные) электроды и замкнем внутреннюю и внешнюю цепь. В цепи возникает электрический ток.

Йодид-ионы отдают свои электроны, которые будут перетекать по проводнику к инертному электроду, погруженному в раствор соли Fe 3+ :

2I — — 2e — = I₂

2Fe 3+ + 2e — = 2Fe 2+

Процессы окисления-восстановления происходят у поверхности инертных электродов. Потенциал, который возникает на границе инертный электрод – раствор и содержит как окисленную, так восстановленную форму вещества, называется равновесным окислительно-восстановительным потенциалом.

Факторы, влияющие на значение окислительно-восстановительного потенциала

Значение окислительно-восстановительного потенциала зависит от многих факторов, в том числе и таких как:

1) Природа вещества (окислителя и восстановителя)

2) Концентрация окисленной и восстановленной форм.

При температуре 25°С и давлении 1 атм. величину окислительно-восстановительного потенциала рассчитывают с помощью уравнения Нернста:

E – окислительно-восстановительный потенциал данной пары;

E°- стандартный потенциал (измеренный при C_ок = C_вос);

R – газовая постоянная (R = 8,314 Дж);

T – абсолютная температура, К

n – количество отдаваемых или получаемых электронов в окислительно-восстановительном процессе;

F – постоянная Фарадея (F = 96484,56 Кл/моль);

C_ок – концентрация (активность) окисленной формы;

C_вос– концентрация (активность) восстановленной формы.

Подставляя в уравнение известные данные и перейдя к десятичному логарифму, получим следующий вид уравнения:

При C_ок > C_вос, E > E° и наоборот, если C_ок 2- , CrO₄ 2- , MnO₄ — ) при уменьшении pH раствора окислительно-восстановительный потенциал возрастает, т.е. потенциал растет с ростом H + . И наоборот, окислительно-восстановительный потенциал падает с уменьшением H + .

4) Температура

При увеличении температуры окислительно-восстановительный потенциал данной пары также растет.

Стандартные окислительно-восстановительные потенциалы представлены в таблицах специальных справочников. Следует иметь ввиду, что рассматриваются только реакции в водных растворах при температуре ≈ 25°С.

Такие таблицы дают возможность сделать некоторые выводы:

Что можно определить по значению окислительно-восстановительного потенциала

• Величина и знак стандартных окислительно-восстановительных потенциалов, позволяют предсказать какие свойства (окислительные или восстановительные) будут проявлять атомы, ионы или молекулы в химических реакциях, например

E°(F₂/2F — ) = +2,87 В – сильнейший окислитель

E°(K + /K) = — 2,924 В – сильнейший восстановитель

Окислительно-восстановительная пара будет обладать тем большей восстановительной способностью, чем больше числовое значение ее отрицательного потенциала, а окислительная способность тем выше, чем больше положительный потенциал.

• Возможно определить какое из соединений одного элемента будет обладать наиболее сильным окислительными или восстановительными свойствами.
• Возможно предсказать направление ОВР. Известно, что работа гальванического элемента имеет место при условии, что разность потенциалов имеет положительное значение. Протекание ОВР в выбранном направлении также возможно, если разность потенциалов имеет положительное значение. ОВР протекает в сторону более слабых окислителей и восстановителей из более сильных, например, реакция

Sn 2+ + 2Fe 3+ = Sn 4+ + 2Fe 2+

практически протекает в прямом направлении, т.к.

E° (Sn 4+ /Sn 2+ ) = +0,15 В,

E° (Fe 3+ /Fe 2+ ) = +0,77 В,

т.е. E° (Sn 4+ /Sn 2+ ) 3+ /Fe 2+ ).

Cu + Fe 2+ = Cu 2+ + Fe

невозможна в прямом направлении и протекает только справа налево, т.к.

В процессе ОВР количество начальных веществ уменьшается, вследствие чего Е окислителя падает, а E восстановителя возрастает. При окончании реакции, т.е. при наступлении химического равновесия потенциалы обоих процессов выравниваются.

• Если при данных условиях возможно протекание нескольких ОВР, то в первую очередь будет протекать та реакция, у которой разность окислительно-восстановительных потенциалов наибольшая.
• Пользуясь справочными данными, можно определить ЭДС реакции.

Как определить электродвижущую силу (ЭДС) реакции?

Рассмотрим несколько примеров реакций и определим их ЭДС:

1. Mg + Fe 2+ = Mg 2+ + Fe
2. Mg + 2H + = Mg 2+ + H₂
3. Mg + Cu 2+ = Mg 2+ + Cu

E° (Mg 2+ /Mg) = — 2,36 В

E° (Fe 2+ /Fe) = — 0,44 В

Чтобы определить ЭДС реакции, нужно найти разность потенциала окислителя и потенциала восстановителя

ЭДС = Е 0 _ок — Е 0 _восст

1. ЭДС = — 0,44 — (- 2,36) = 1,92 В
2. ЭДС = 0,00 — (- 2,36) = 2,36 В
3. ЭДС = + 0,34 — (- 2,36) = 2,70 В

Все вышеуказанные реакции могут протекать в прямом направлении, т.к. их ЭДС > 0.

Связь константы равновесия и окислительно — восстановительного потенциала

Если возникает необходимость определения степени протекания реакции, то можно воспользоваться константой равновесия.

Например, для реакции

Zn + Cu 2+ = Zn 2+ + Cu

Применяя закон действующих масс, можно записать

Здесь константа равновесия К показывает равновесное соотношение концентраций ионов цинка и меди.

Значение константы равновесия можно вычислить, применив уравнение Нернста

Подставим в уравнение значения стандартных потенциалов пар Zn/Zn 2+ и Cu/Cu 2+ , находим

В состоянии равновесия E 0 _Zn/Zn2+ = E 0 _Cu/Cu2+, т.е.

-0,76 + (0,59/2)lgC_Zn2+ = +0,34 + (0,59/2)lgC_Cu2+, откуда получаем

Значение константы равновесия показывает, что реакция идет практически до конца, т.е. до того момента, пока концентрация ионов меди не станет в 10 37,7 раз меньше, чем концентрация ионов цинка.

Константа равновесия и окислительно-восстановительный потенциал связаны общей формулой:

lgK = (E₁ 0 -E₂ 0 )n/0,059, где

K — константа равновесия

E₁ 0 и E₂ 0 – стандартные потенциалы окислителя и восстановителя соответственно

n – число электронов, отдаваемых восстановителем или принимаемых окислителем.

Если E₁ 0 > E₂ 0 , то lgK > 0 и K > 1.

Следовательно, реакция протекает в прямом направлении (слева направо) и если разность (E₁ 0 — E₂ 0 ) достаточно велика, то она идет практически до конца.

Напротив, если E₁ 0 0 , то K будет очень мала.

Реакция протекает в обратном направлении, т.к. равновесие сильно смещено влево. Если разность (E₁ 0 — E₂ 0 ) незначительна, то и K ≈ 1 и данная реакция не идет до конца, если не создать необходимых для этого условий.

Зная значение константы равновесия, не прибегая к опытным данным, можно судить о глубине протекания химической реакции. Следует иметь ввиду, что данные значений стандартных потенциалов не позволяют определить скорость установления равновесия реакции.

По данным таблиц окислительно-восстановительных потенциалов возможно найти значения констант равновесия примерно для 85000 реакций.

Как составить схему гальванического элемента?

Приведем рекомендации ИЮПАК, которыми следует руководствоваться, чтобы правильно записать схемы гальванических элементов и протекающие в них реакции:

1. ЭДС элемента — величина положительная, т.к. в гальваническом элементе работа производится.
2. Значение ЭДС гальванической цепи – это сумма скачков потенциалов на границах раздела всех фаз, но, учитывая, что на аноде происходит окисление, то из значения потенциала катода вычитают значение потенциала анода.

Таким образом, при составлении схемы гальванического элемента слева записывают электрод, на котором происходит процесс окисления (анод), а справа – электрод, на котором происходит процесс восстановления (катод).

1. Граница раздела фаз обозначается одной чертой — |
2. Электролитный мостик на границе двух проводников обозначается двумя чертами — ||
3. Растворы, в которые погружен электролитный мостик записываются слева и справа от него (если необходимо, здесь же указывается концентрация растворов). Компоненты одной фазы, при этом записываются через запятую.

Например, составим схему гальванического элемента, в котором осуществляется следующая реакция:

Fe 0 + Cd 2+ = Fe 2+ + Cd 0

В гальваническом элементе анодом является железный электрод, а катодом – кадмиевый.

Анод Fe 0 |Fe 2+ || Cd 2+ |Cd 0 Катод

Типичные задачи на составление схем гальванического элемента и вычисление ЭДС реакции с решениями вы найдете здесь.

📽️ Видео

Гальванические элементы. 1 часть. 10 класс.Скачать

Электродные потенциалы металлов. Электроды сравненияСкачать

Электрохимический ряд потенциалов. 1 часть. 10 класс.Скачать

Использование таблиц потенциалов и расчет ЭДС реакции. Продукты в ОВР. Ч.5-1.Скачать

Продукты в ОВР. Ч.2-1. Электродный потенциал металлов.Скачать

Шеховцова Т.Н. - Аналитическая химия - Окислительно-восстановительные реакцииСкачать

ОВР часть 2. Окислительно-восстановительные реакции. Электродный потенциал.Скачать

Потенциал покоя и равновесный потенциалСкачать

Гальванические элементыСкачать

Гудилин Е. А. - Неорганическая химия I - Окислительно-восстановительные реакцииСкачать

Румянцева М.Н.- Общая и неорганическая химия. Лекции - 5.Окислительно-восстановительные процессыСкачать

Составление схемы и вычисление ЭДС гальванического концентрационного элемента | Уравнение НернстаСкачать

Задачи на гальванический элемент. Продукты в ОВР. Ч.5-4.Скачать

Продукты в ОВР. Ч.2-2. Окислительно-восстановительный (редокс) потенциал в растворе.Скачать