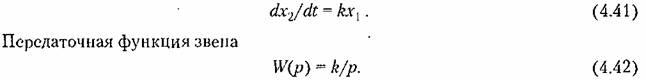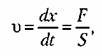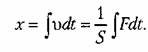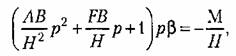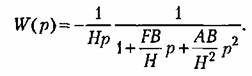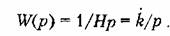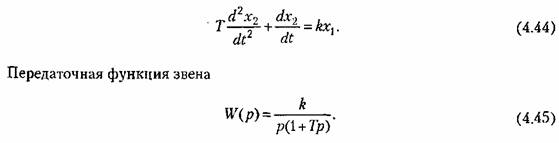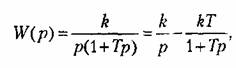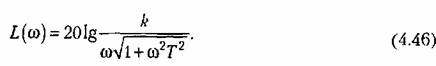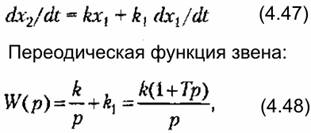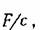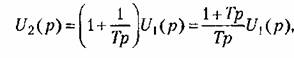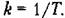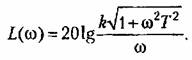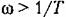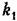Реальное интегрирующее звено дифференциальное уравнение (7 видео)

Интегрирующие звенья

1. Идеальное интегрирующее звено. Звено описывается дифференциальным уравнением

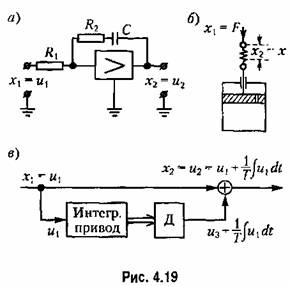
Такое звено является идеализацией реальных интегрирующих звеньев, часть которых будет рассмотрена ниже. Примеры интегрирующих звеньев приведены на рис. 4.18. Часто в качестве такого звена используется операционный усилитель в режиме интегрирования (рис. 4.18, а). Интегрирующим звеном является также обычный гидравлический демпфер (рис. 4.18, б). Входной величиной здесь является сила F, действующая на поршень, а выходной — перемещение поршня х2. Так как скорость движения поршня пропорциональна приложенной силе (без учета инерционных сил):

где 5 — коэффициент скоростного сопротивления; его перемещение будет пропорциональным интегралу от приложенной силы:

Часто в качестве интегрирующего звена используется интегрирующий привод (рис, 4.18, г). Это особенно удобно делать при необходимости длительного иитегрирования

(часы, дни и даже месяцы), например в автоматических путепрокладчиках и навигационных системах.

(в зоне линейности).

Из уравнений гироскопа, приведенных в предыдущем параграфе, можно получить:

откуда передаточная функция для угла прецессии

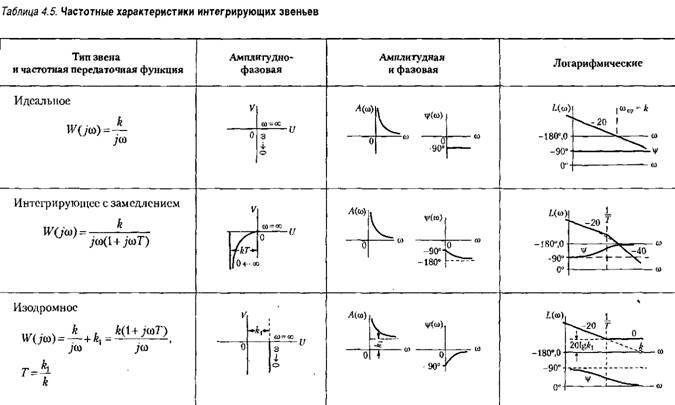
Временные характеристики звена приведены в табл. 4.4, а частотные — в табл. 4.5.

Амплитудно-фазовая характеристика сливается с отрицательной частью мнимой оси.

Построение л, а. х. делается но выражению

, параллельную вещественной оси.

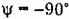
2. Интегрирующее звено с замедлением. Звено описывается дифференциальным уравнением

Примером такого звена является двигатель (рис. 4.10, а), если в качестве выходной величины рассматривать не угловую скорость, а угол поворота, являющийся интегралом от угловой скорости. К такому же типу звена сводятся демпфер (рис. 4.18, 6) серводвигатель (рис. 4.18, в), интегрирующий привод (рис. 4,18, г), если более точно рассматривать их уравнения движения, и др.

Интегрирующее звено с замедлением можно представить как совокупность двух включенных последовательно звеньев — идеального интегрирующего и апериодического первого порядка.

Для нахождения временных характера удобно передаточную функцию представить в виде алгебраической суммы

что позволяет представить решение дифференциального уравнения (4.44) в виде суммы решений для идеального интегрирующего звена и апериодического звена нервого порядка.

Временные характеристики приведены в табл.

4.4, а частотные — в табл. 4.5.

Л.а.х. строится по выражению

и -40 дБ/дек (при со > 1/7). 3. Изодромное звено. Звено описывается уравнением

— постоянная времени изодромного звена.

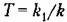
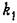
где с — жесткость пружины, и перемещения поршня

где 5 — коэффициент скоростного сопротивления демпфера.

точки

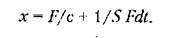
При использовании операционного усилителя (рис. 4.19, а) изодромное звено может быть получено посредством применения КС-цепи в обратной связи.

Таким образом, для схемы, изображенной на рис. 4.19, в,

Временные характеристики звена представлены в табл. 4.4, а частотные — в табл. 4.5.

Л. а. х. строится по выражению

Из рассмотрения л. а. х. и л. ф. х. видно, что в области малых частот (меньших, чем сопрягающая частота) звено ведет себя как идеальное интегрирующее и тем точнее, чем меньше частота.

Свойство звена вводить интегрирующее действие в области малых частот используется для улучшения качественных показателей систем автоматического регулирования (см. главу 9).

Содержание

3. Частотные характеристики звеньев и систем автоматического управления. ч. 3.2 Простейшие типовые звенья
3.2.1. Идеальное усилительное звено
3.2.2. Идеальное дифференцирующее звено
3.2.3. Идеальное интегрирующее звено
Пример интегрирующего и дифференцирующего звена на основе конденсатора
Типовые звенья: интегрирующее и дифференцирующее
🔥 Видео

Видео:12) ТАУ для чайников. Часть 4.4. Интегрирующее звено.Скачать

3. Частотные характеристики звеньев и систем автоматического управления. ч. 3.2 Простейшие типовые звенья

Лекции по курсу «Управление Техническими Системами» читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки» факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность!

Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

Тема сегодняшней статьи:
3.2. Типовые звенья систем автоматического управления (регулирования). Классификация типовых звеньев. Простейшие типовые звенья.

Хочешь вкусить плодов познания? — Грызи гранит науки!

Понятие “типовые звенья” в теории управления техническими системами, в основном, связано с описанием САУ (САР) в переменных “вход – выход”, т.е. описание систем в передаточных функциях. Любую линейную САУ (САР) или линеаризованную САР можно структурно расчленить на простейшие элементы (звенья), соединенные между собой соответствующими последовательными, параллельными связями, местными и локальными обратными связями, сумматорами, сравнивающими устройствами и т.д.

Достигнуто общепринятое соглашение, что наиболее удобно расчленять структурную схему САР на звенья 1-го и 2-го порядков. Принято называть такие простейшие звенья типовыми.

С другой стороны, реальная линеаризованная (линейная) система состоит из набора отдельных узлов и агрегатов, соединенных соответствующими связями, причем порядок уравнений динамики вышеуказанных узлов и агрегатов может быть и выше второго. В этом случае звенья (узлы и агрегаты) САР можно классифицировать по их свойствам.

Различают 3 типа звеньев:

Существуют также особые звенья, которые будут рассмотрены позднее.

Учитывая, что передаточная функция линейного (линеаризованного) звена может быть записана как:

где: и — полиномы по степеням s, причем коэффициенты при низшей степени s в полиномах , равны 1, классификацию на типы звеньев можно объяснить видом полиномов или (что эквивалентно) видом коэффициентов в соответствующих уравнениях динамики звена.
Подробнее о передаточной функции см. здесь.

Позиционным звеном считают звено, в котором полиномы N(s) и L(s) содержат свободные члены (равные 1). Например:

или в уравнении динамики (x(t) – входной сигнал, y(t) – выходной):

Из типовых звеньев (1-го и 2-го порядка) к позиционным звеньям относятся: идеальное усилительное звено, апериодические звенья 1-го и 2-го порядка, колебательное звено и форсирующее звено.

Дифференцирующим звеном считается звено, в котором полином L(s) содержит свободный член (равный 1), а полином N(s) не содержит свободного члена ().
Например:

или в уравнении динамики:

Из типовых звеньев к дифференцирующим звеньям относятся идеальное дифференцирующее звено, инерционно-дифференцирующее звено.

Интегрирующим звеном считается звено, в котором полином N(s) содержит свободный член (), а полином L(s), не содержит свободного члена (). Например:

или в уравнении динамики:

Из типовых звеньев к интегрирующим звеньям относятся идеальное интегрирующее звено, инерционно–интегрирующее звено.

Пример переходного процесса при единичном ступенчатом воздействии на три разных звена, приведенных выше:

3.2.1. Идеальное усилительное звено

Уравнение динамики каждого звена имеет вид: , т.е. уравнение не является дифференциальным, следовательно, данное звено является безынерционным.

Переходя к изображениям , получаем:
– уравнение динамики звена в изображениях.
Передаточная функция идеального усилительного звена:

АФЧХ не зависит от ω, поскольку:

Рисунок 3.2.1 АФЧХ идеального усилительного звена

Годограф АФЧХ “вырождается” в точку: U(ω) =K; V(ω) =0;
A(ω) ≡modW(iω) =│W(iω)│=K =>
Lm(ω)=20lgA(ω) =20lgK; =>
φ(ω) = const = 0 т.е. фазового сдвига нет. Следовательно, данное звено является безынерционным, чисто усилительным звеном.

Рисунок 3.2.4 ЛАХ идеального усилительного звена

Найдем весовую w(t) и переходную h(t) функции звена (подробнее см. здесь).
Весовая функция:

3.2.2. Идеальное дифференцирующее звено

Уравнение динамики звена имеет вид:

где: – постоянная времени.

Переходя к изображениям:

Уравнение динамики звена в изображениях:

Передаточная функция идеального дифференцирующего звена:

Графики годографа АФЧХ, A(ω) и φ(ω) имеют вид:

Логарифмическая амплитудная характеристика ЛАХ::

Из рисунка 3.2.9 видно, что данное звено обеспечивает опережение по фазе на /2 (при любой частоте входного сигнала).

Чем выше частота единичного гармонического сигнала на входе в звено, тем выше амплитуда выходного сигнала в установившемся режиме.

Найдем весовую функцию звена:

Учитывая, что δ(t) имеет вид как на рис.3.2.11 (зависимость показана утрированно), а весовая функция пропорциональна производной от δ(t):

Найдем переходную функцию звена:

Иногда идеальное дифференцирующее звено представляется в виде или . В последнем варианте коэффициент К имеет смысл постоянной времени.

3.2.3. Идеальное интегрирующее звено

Уравнение динамики такого звена имеет вид:

или в изображениях:

Передаточная функция идеального интегрирующего звена:

Умножая числитель и знаменатель на i, получаем:

Годограф АФЧХ имеет вид:

Данное звено всегда дает отставание по фазе на угол .

Найдем весовую функцию звена:

Найдем переходную функцию звена:

Примерами устройств, близких к идеальному усилительному звену, можно считать: широкополосный электронный усилитель (приближенно), механический редуктор без учета инерционности и нелинейных эффектов, жесткую механическую муфту и т.д.

Примером идеального дифференцирующего звена можно считать тахогенератор:

где u(t) – напряжение на клеммах тахогенератора, φ(t) – угол поворота якоря (ротора) тахогенератора.

Примером идеального интегрирующего звена можно считать большинство электродвигателей (без учета инерционности якоря), где входным воздействием считать напряжение в обмотке возбудителя (двигателем постоянного тока), а выходным воздействием – угол поворота выходного вала.

Пример интегрирующего и дифференцирующего звена на основе конденсатора

Один и тот же технический элемент, с точки зрения теории автоматического управления, может выступать как в качестве интегрирующего, так и в качестве дифференцирующего звена.

В качестве примера интегрирующего звена можно рассмотреть конденсатор, где входным воздействием является ток, а выходным результатом является напряжение на клеммах конденсатора. Действительно, при малом токе и большой емкости конденсатора, в случае ступенчатого изменения тока с 0, мы получаем график напряжения, совпадающий по форме с переходной функцией интегрирующего звена. На рисунке 3.2.20 представлена такая модель, где ток ступенькой меняется на пятой секунде расчета.

Если построить с помощью гармонического анализатора ЛАХ и ФЧХ, мы увидим, что угол наклона ЛАХ составляет -20 dB/dec, а угол сдвига фазы равен — или -90 градусов на графике (см. рис. 3.2.21).

Тот же самый конденсатор, при определенных параметрах сети, может выступать в качестве идеального дифференцирующего звена, если в качестве входного воздействия подавать напряжение, а в качестве результирующей величины использовать ток в цепи.

Электрическая схема использования конденсатора в качестве дифференцирующего звена с гармоническим анализатором приведена на рисунке 3.2.22. На графиках гармонического анализатора видно, что угол наклона ЛАХ составляет 20 dB/dec, а угол сдвига фазы равен или 90 градусов на графике.

Примеры моделей, использованные в данной лекции, можно взять в этом архиве.

Видео:12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать

Типовые звенья: интегрирующее и дифференцирующее

Интегральными звеньями называются такие звенья, в которых выходная величина пропорциональна интегралу во времени от входной величины. Дифференциальное уравнение интегрирующего звена имеет вид:

dy/dt=kx, Из уравнения следует, что в интегрирующем звене скорость изменения выходной величины пропорциональна входной величине.

Передаточная функция интегрирующего звена: Py=kx; y/x=k/P; W(p)=k/P; Переходная характеристика интегрирующего звена показана на рис.

В отличие от других звеньев, интегрирующее звено не приходит в равновесное состояние при скачкообразном изменении входной величины. Если усилительное, апериодическое, колебательное звенья имеют статическую характеристику, и, следовательно, в равновесных состояниях — однозначную зависимость выходной величины от входной, то интегрирующее звено этого не имеет. Поэтому усилительное, апериодическое и колебательные звенья называются статическими, а интегрирующее — астатическим. Уравнениями интегрирующего звена описывается поведение ненагруженных электродвигателей, которые быстро набирают обороты, нагревательных элементов, операционных усилителей.Дифференциальное звено

Называется такое типовое звено, в котором выходная величина пропорциональна производной во времени от входной величины. Различают идеальные и реальные дифференциальные звенья. Идеальные дифференциальные звенья характеризуются следующим уравнением: y=k*dx/dt; y=kPx; y/x=kP; W(p)=kP. Практически нет идеальных звеньев, так как возмущение на вход звена нельзя подать мгновенно. Рис. Уравнение реального дифференциального звена: T*(dy/dt)+y=kT*(dx/dt); Переходный процесс в реальном звене при подаче на вход скачкообразного возмущения описывается интегральным уравнением: y=kxe^-t/T; Передаточная функция: TPy+y=kTPx; y(TP+1)=kTPX; W(p)=y/x=kTP/TP+1; Чем больше значение коэффициента k, тем ближе такое звено к идеальному дифференцирующему звену. Чем больше T, тем ближе реальное звено к идеальному усилительному звену. Таким образом, реальное дифференциальное звено занимает промежуточное положение между усилительным и идеальным дифференциальным звеном, в зависимости от величин T и k.

Выше рассматривались звенья только с одной входной и одной выходной величинами. Однако большое число реальных химико-технологических объектов, а также систем регулирования представляют собой соединения звеньев, имеющих несколько входных и выходных величин. Анализ таких звеньев более сложен

БИЛЕТ

Термоэлектрические термометры (термопары).

Первичным преобразователем (датчиком) термоэлектрического термометра служит термопара, состоящая из двух разнородных проводников

Принцип действия термопары основан на термоэлектрическом эффекте, заключающемся в том, что в замкнутой цепи, состоящей из двух или нескольких разнородных проводников, возникает электрический ток, если хотя бы два места соединения (спая) проводников имеют разную температуру.

Спай с температурой t называется рабочим (горячим) и помещается в зону измерения температуры, а второй спай с постоянной температурой t₀ — свободным (холодным), эта чаще всего температура того места, где находится измерительный прибор. Проводники A и B называются термоэлектродами.

Термоэлектрический эффект объясняется присутствием в металле свободных электронов, число которых в единице объема различно для разных металлов.

Электрическое поле, возникающее в месте соприкосновения проводников, препятствует этой диффузии, и когда скорость диффузии электронов станет равна скорости их перехода из металла В в металл А, наступит состояние подвижного равновесия. В таком состоянии между электродами А и В возникает некоторая разность потенциалов.

Промышленные типы термопар.

Платинородий(10% родия)-платиновая термопара (тип ТПП) (от 0 до 1300 0 С) надежно работает в нейтральной и окислительной средах, но быстро разрушается в восстановительной атмосфере, особенно в присутствии окислов металла и кремнезема вблизи термопары. Вредно действуют на платину пары металла и углерод (особенно окись углерода). Поэтому при промышленных измерениях необходима тщательная изоляция термопары от непосредственного воздействия измеряемой среды. Термопара ТПП при правильной эксплуатации сохраняет постоянство своей градуировки в течение весьма длительного времени. Однако т.э.д.с., этой термопары мала по сравнению с другими термопарами. Термопары ТПП применяются при температурах до 1600 0 С.

Платинородий (30% родия) — платинородиевая (6% родия) термопара (тип ТПР) (от 300 до 1600 0 С). Особенность термопары в том, что она применяется для измерения самых высоких температур — до 1800 0 С и развивает очень малую т.э.д.с. (0,04 мВ при 120 0 С и 0,002 мВ при 20 0 С).

Термопары платиновой группы ТПП и ТПР изготовляются обычно в виде проволоки диаметром 0,5 или 1 мм и изолируются фарфоровыми бусами или фарфоровыми трубками.

Хромель-алюмелевая термопара (типа ТХА) (от –50 до 1000 0 С) наиболее устойчива из всех неблагородных термопар. Она применяется для измерения температуры до 1300 0 С. Зависимость т.э.д.с. этой термопары от температуры близка к линейной. Большое содержание никеля в сплаве обеспечивает стойкость термопары против окисления и коррозии. Восстановительная среда вредно действует на хромель-алюмелевую термопару.

Термопара из сплавов НК-СА (типа ТНС) обладает характерной особенностью, заключающейся в том, что она не требует введения поправки на температуру холодных спаев, так как т. э.д.с., развиваемая термопарой до 200 0 С, практически равна нулю. Верхний температурный предел 1000 0 С.

Хромель(89% Ni)-копелевая(45% Ni) термопара (типа ТХК) (от-50 до 600 0 С) развивает наибольшую т.э.д.с. из всех стандартных термопар, что позволяет изготовлять термоэлектрические термометры с узкой температурной шкалой. Применяется для измерения температуры до 800 0 С. Стандартные термопары ТХА, ТНС, ТХК изготовляются из проволоки диаметром 0,7–3,2 мм и изолируются керамическими бусами.