Решение
а) Проверим две версии: I. реакция имеет первый порядок и II. реакция имеет второй порядок. Линейные формы интегральных уравнений в этих случаях, соответственно, таковы (17.8 и 17.25):
I. ln c = ln c 0 – kt ; II. 1/c = 1/ c 0 + kt . (IV.23,a-б)
Таким образом, по мере увеличения t
— в реакциях первого порядка происходит линейное убывание ln c ,
— а в реакциях второго порядка – линейное возрастание 1/c .
б) Составляем по имеющимся данным таблицу:
| tx , мин | 0 | 3 | 5 | 7 | 10 | 15 |
| ln c2 | –4,6 | –4,9 | –5,06 | –5,2 | –5,37 | –5,61 |
| (Δln c2) / Δt | – | –0,1 | –0,08 | –0,07 | –0,05 | –0,048 |
| (1/c2 ) ∙10 –2 | 1,0 | 1,35 | 1,58 | 1,82 | 2,16 | 2,75 |
| Δ(1/c2 ) ∙10 –2 / Δt | – | 0,117 | 0,115 | 0,112 | 0,113 | 0,118 |
в) Видно, что скорость изменения ln c2 (третья строка таблицы) не остаётся постоянной: в конце периода наблюдения она вдвое меньше, чем вначале.
Скорость же изменения 1/c2 (последняя строка) гораздо более постоянна. Значит, зависимость 1/c2 от t – практически линейная. И, следовательно, порядок реакции – второй.
 |
г) Для нахождения константы скорости возьмём первую и последнюю точки зависимости 1/c от t и будем исходить из формулы (17.25):
10. Дана реакция разложения аммиака:
Она проходит на горячей вольфрамовой проволоке при температуре Т = 1129 К. Объём и температура системы – постоянны. О скорости реакции судили по изменению общего давления в системе (ΔР):
| T, cек | |||||
| ΔР∙10 –2 , Па | 14,66 | 29,23 | 59,70 | 89,6 | 117,2 |
Начальное давление в системе – Po = 266,6 ∙10 2 Па. Именно от него отсчитаны все приведённые в таблице значения ΔР (т.е. ΔР i = Рi – Po ).
Определить порядок реакции и константу скорости.
Решение
а) Из уравнения Клайперона-Менделеева следует, что давление газа прямо пропорционально его (газа) молярной концентрации (3.23):
В случае смеси газов это соотношение верно,
-во-первых, для общего давления и общей концентрации,
-а во-вторых, для парциального давления и парциальной концентрации каждого газа.
б) Из уравнения (IV.25) следует, что исчезновение двух молекул аммиака приводит к появлению четырёх молекул азота и водорода. Поэтому общее давление в системе возрастает.
в) Запишем баланс давления и выразим все его компоненты через изменение давления аммиака:
Таким образом, изменение давления NH3 связано с изменением общего давления простым соотношением:
Это позволяет проследить, как падает в системе парциальное давление аммиака (на фоне общего роста давления):
г) Составим таблицу, включающую рассчитанные таким образом значения Р(NH3), а также ln Р(NH3) (проверка версии о первом порядке реакции) и 1/ Р(NH3) (проверка версии о втором порядке).
| t, сек | 0 | 100 | 200 | 400 | 600 | 800 |
| Р(NH3)∙10 –2 , Па | 266,6 | 251,9 | 237,3 | 206,9 | 177,0 | 149,4 |
| ΔР(NH3)∙10 –2 /Δt | – | –0,147 | –0,146 | –0,152 | –0,150 | –0,138 |
| ln Р(NH3) | 10,19 | 10,13 | 10,07 | 9,94 | 9,78 | 9,61 |
| Δln Р(NH3) /Δ0,01t | – | –0,060 | –0,060 | –0,065 | –0,080 | –0,085 |
| [1/ Р(NH3)] ∙10 5 | 3,75 | 3,97 | 4,21 | 4,83 | 5,65 | 6,69 |
| Δ[1/ Р(NH3)] ∙10 7 /Δt | – | 0,22 | 0,24 | 0,31 | 0,41 | 0,52 |
— скорость изменения величины 1/ Р(NH3) (самая нижняя строка) со временем значительно возрастает,
— скорость изменения величины ln Р(NH3) (третья снизу строка) также обнаруживает явную тенденцию к увеличению (по модулю).
Значит, гипотезы о первом или втором порядке реакции не подтверждаются.
е) Зато достаточно стабильна скорость изменения Р(NH3), т.е. давление (а значит, и концентрация) аммиака линейно зависит от времени. Это соответствует нулевому порядку реакции (рис. 17.1).
Данное обстоятельство вполне объяснимо: рассматриваемая реакция – каталитическая (катализатором служит вольфрамовая проволока), и, по-видимому, её скорость ограничивается в предложенных обстоятельствах исключительно количеством катализатора (доступностью проволоки для молекул аммиака).
ж) Для расчёта константы скорости используем начальную и, например, третью точку (400 с). Предварительно перейдём к молярным концентрациям аммиака:
Тогда, исходя из формулы (17.3), получаем:
k = (c 0 – c3 )/ t3 ≈ 1,6∙10 –6 M/c . (IV.30)
11. Дана реакция образования фосгена:
СО + Cl2 →COCl2 . (IV.31)
Она происходит при освещении исходной газовой смеси монохроматическим светом с длиной волны λ = 400 нм. В частности, при поглощении лучистой энергии Ефот = 300 Дж образовалось mпрод = 0,1 кг фосгена.
Дата добавления: 2016-03-20 ; просмотров: 5294 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
- Физическая и коллоидная химия (стр. 21 )
- Краткое содержание главы 22
- Решение
- Решение
- Для этого смешали равные объёмы 1 М растворов указанных реагентов. Через tх = 2ч анализ показал, что в реакционной среде присутствует муравьиная кислота в концентрации схпр = 0,214 М.
- Решение
- Решение
- При температуре Т1 = 273 К константа скорости равна k1 = 1,17 1/(M ∙ мин) , а при температуре Т2 = 298 К k2 = 6,56 1/(M ∙ мин) . Найти энергию активации, Еак.
- Решение
- Решение
- Вычисления производить с помощью правила Вант-Гоффа. Температурный коэффициент реакции – γ = 3.
- Решение
- Решение
- Необходимые исходные сведения и основные уравнения
- 🎦 Видео
Видео:Диффузия аммиака.Скачать

Физическая и коллоидная химия (стр. 21 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Это-то и приводит к понижению сS(Ох) – приэлектродной концентрации вещества Ох. Одновременно здесь же возрастает концентрация восстановленной формы, сS(Rd). Заметим: отсюда следует, что пара Ox/Rd тоже вносит вклад в электродную поляризацию.
г) По мере увеличения потенциала рабочего электрода последний со всё большей лёгкостью отдаёт электроны на восстановление Ox в Rd. Поэтому концентрация сS(Ох) становится всё меньше, а диффузионный ток, согласно законам Фика, всё выше.
 |
д) Но рост тока происходит не беспредельно, а до тех пор, пока сS(Ох) не снизится практически до нуля. Следовательно, максимальный диффузионный ток определяется величиной
где cср — средняя концентрация формы Ох в системе.
5. а) В итоге, график зависимости тока от потенциала рабочего электрода будет описываться S-образной кривой, начинающейся от I0 и стремящейся к Imax. Последнюю величину иногда называют диффузионным током, хотя, как мы видим, это не совсем точно: диффузионным ток является почти на всём протяжении графика (начиная с I0).
Получающаяся кривая (см. рис. 22.6) называется полярографической волной.
 |
б) S-образность предполагает наличие точки перегиба. В данном случае такая точка соответствует
При этом концентрации форм Ox и Rd в приэлектродном пространстве одинаковы.
в) Следовательно, потенциал электрода в точке перегиба – это стандартный потенциал соответствующей редокс-пары:
 |
В полярографии данное значение называют потенциалом полуволны.
22.8. Анализ полярографической кривой
1. Нетрудно установить аналитическую связь между потенциалом и током,
т. е. формулу, которая описывает полярографическую волну.
а) Так, при начальном токе в приэлектродном пространстве присутствует только вещество Ох (в той же концентрации, что и в других точках ячейки), а вещество Rd — отсутствует. Запишем это так:
 |
б) Аналогично для точки перегиба и для максимального тока можно записать:
 |

 |
г) Следовательно, уравнение Нернста (14.22,б) приобретает вид:
Эта формула и описывает S-образную зависимость Ψ от I или, наоборот, зависимость I от Ψ.

 |
Использование этой формы уравнения показано на рис. 22.8.
б) А от чего зависит величина Imax?
 |
I. Как следует из формулы
она пропорциональна средней концентрации в растворе исследуемого вещества.
 |
II. Более точное выражение для Imax — уравнение Ильковича. Но и в нем зависимость Imax от концентрации линейна:
где KИ — константа Ильковича, имеющая достаточно сложную структуру.
3. а) Из сказанного вытекают, по крайней мере, две возможности, открывае-
мые полярографией:
— определение концентрации исследуемого вещества (по значению Imax, а точнее, по разности Imax – I0);
— и определение стандартного потенциала (Ψ0 = Ψ½) какой-либо окислительно-восстановительной пары (по значению I½).
б) Причем, если в растворе — смесь веществ, существенно отличающихся по значениям ψ0 соответствующих OB-пар, то на полярограмме получается целая
серия полярографических волн (рис. 22.9). По высоте каждой из них можно определить концентрацию соответствующих веществ, т. е. предварительного разделения веществ в этом случае не требуется.
Краткое содержание главы 22
В главе рассмотрена кинетика процессов, проходящих в гальванических элементах и при электролизе.
1. В этих процессах велика роль ДИФФУЗИИ: от коэффициента диффузии D зависят и коэффициент сопротивления среды, и электрическая подвижность частиц:
 |
2. а) Поэтому при электролизе параметр D влияет на каждую из двух составляющих плотности тока – i = iэл + iдиф .
 |
б) В целом же величина ионного тока определяется формулой:
в) А концентрация реагирующих ионов вычисляется по формуле:
 |
В зависимости от соотношения параметров B’и k эта концентрация может быть больше или меньше, чем вдали от электрода.
 |
3. а) Масса вещества, реагирующего при электролизе, равна
 |
б) Здесь различают ПЕРВЫЙ И ВТОРОЙ ЗАКОНЫ ЭЛЕКТРОЛИЗА:
4. Рассмотрено также явление ЭЛЕКТРОДНОЙ ПОЛЯРИЗАЦИИ. При прохождении тока через раствор электролита разность потенциалов отклоняется от равновесного значения. Это сопровождается изменением концентраций реагентов и продуктов в приэлектродном пространстве.
5. Наконец, мы познакомились с ПОЛЯРОГРАФИЕЙ.
 |
а) В данном методе исследования раствор подвергают электролизу в таких условиях, при которых остаётся только одна составляющая тока – диффузионная:
б) При повышении потенциала рабочего электрода концентрация ионов возле него снижается; поэтому градиент концентрации, а с ним и диффузионный ток, возрастают.
в) Рост тока идет до предельного уровня Imax, который зависит от общей концентрации реагирующего иона:
 |
г) Перегиб же кривой зависимости I от потенциала соответствует стандартному значению потенциала.
д) Путем полярографии можно определить концентрацию вещества (по Imax) и стандартный потенциал пары (по I½).
ЗАДАЧИ К РАЗДЕЛУ 4
1. В водном растворе происходит разложение пероксида водорода:
Процесс идёт как реакция первого порядка (это оговаривается специально, поскольку возможно и ферментативное разложение Н2О2 каталазой в режиме насыщения, чему соответствует нулевой порядок реакции; п. 20.6).
Константа скорости – k = 0,05081 1/мин. Определить период полупревращения (Т½) и время, за которое распадётся 99,9% Н2О2 ( t 99,9%).
Видео:Смещение равновесия в растворе аммиака при нагреванииСкачать

Решение
а) Используем формулы для необратимых реакций первого порядка (п. 17.1). Так, согласно (17.10,б),
б) А уравнение (17.9,а) для искомого времени t 99,9% приобретает вид:
Заметим: время распада 99,9% пероксида водорода в 10 раз больше периода полупревращения.
2. Пусть в растворе проходит реакция (IV.1). Количество оставшегося пероксида водорода определяют путём титрования проб раствором KMn04. На титрование начальной пробы ушло V0 = 22,8 мл р-ра KMn04 .
Какой объём титранта (Vx) потребуется для титрования пробы (равной по объёму с начальной) через tx = 20 мин после начала реакции?
Считать, что константа скорости реакции (k) при выбранной температуре проведения эксперимента неизвестна, а период полупревращения Н2О2 – Т½ = 14 мин.
Видео:Определение порядка реакции методом подбора кинетического уравненияСкачать

Решение
а) Из интегрального уравнения реакций первого порядка (17.9,б) найдём отношение концентраций Н2О2 – на момент tx и начальной:
б) Очевидно, таково же отношение и объёмов KMn04, требующихся для полного оттитровывания Н2О2 :
3. Проводится реакция между пероксидом водорода и формальдегидом:
Н2О2 + Н2С=О → НСООН + Н2О (IV.6)
Видео:07 Кинетика 5 эксп опред параметров реакцииСкачать

Для этого смешали равные объёмы 1 М растворов указанных реагентов. Через tх = 2ч анализ показал, что в реакционной среде присутствует муравьиная кислота в концентрации схпр = 0,214 М.
Найти константу скорости реакции (k) и время, за которое прореагирует 90% исходных веществ (t 90%).
Видео:ЛЕКЦИЯ №2 || Химическая кинетика || Скорость реакции, Закон действия масс, Порядок реакцииСкачать

Решение
а) Заметим, что после смешивания растворов реагентов концентрация каждого из них стала равной с0А = с0В ≡ с0 = 0,5 М.
Муравьиная кислота – один из продуктов реакции. Поэтому на момент tх концентрация каждого реагента снижается до уровня
б) Теперь используем формулы для необратимых реакций второго порядка (п. 17.3). Согласно (17.25),
 |
в) А чтобы найти t90% , из последнего соотношения выразим время и подставим сх = 0,1с0:
4. Пусть проходит некая реакция второго порядка:
Её энергия активации – Еак = 23,1 кДж/моль. При температуре Т1 = 300 К за t1 = 1ч успевает прореагировать ζ1 = 95 % реагентов.
Найти температуру Т2 , при которой за t2 = 1 мин прореагирует ζ2 = 77,5 % тех же веществ, взятых в тех же начальных концентрациях.
Видео:Механизм реакции РАДИКАЛЬНОГО ЗАМЕЩЕНИЯ у АЛКАНОВСкачать

Решение
а) Выразим концентрации реагента А (или В – это неважно), достигаемые к указанному моменту времени, через долю уже прореагировавшего вещества:
 |
б) Запишем формулу вида (IV.8,б) для константы скорости при температуре Т1, затем – при искомой температуре Т2 , и поделим второе выражение на первое:
 |
в) И, наконец, используем один из вариантов уравнения Аррениуса, связывающий две температуры и соответствующие им значения константы скорости. Из формулы (18.27) имеем:
Видео:Вычисление константы скорости реакции | Задачник по химии ГлинкаСкачать

При температуре Т1 = 273 К константа скорости равна k1 = 1,17 1/(M ∙ мин) , а при температуре Т2 = 298 К k2 = 6,56 1/(M ∙ мин) . Найти энергию активации, Еак.
Видео:Балка. Реакции в заделке. Реакции опор. Сопромат.Скачать

Решение
 |
Опять обращаемся к формуле (18.27). Из неё можно сразу выразить Еак :
6. Пусть происходит термическое разложение этана (как реакция первого порядка). При температуре Т1 = 823 К константа скорости равна k1 = 2,5∙105 1/с , а при температуре Т2 = 903 К k2 = 141,5∙105 1/с .
Найти период полупревращения (Т½) при температуре Т3 = 873 К.
Видео:Механизмы реакций замещения. Радикальное/электрофильное/нуклеофильное замещение.Скачать

Решение
а) Логарифмические формы уравнений Аррениуса (18.24), Клаузиуса-Клайперона (7.22,б) и изобары химической реакции Вант-Гоффа (5.16) в математическом отношении совершенно одинаковы: они дают зависимость от температуры, соответственно, константы скорости реакции (ki), давления насыщенного пара (Pнас) и константы равновесия реакции (Кр) в одном и том же виде:
Поэтому подходы к решению задач из разных разделов физической химии могут быть тоже одинаковыми.
 |
б) В данном случае можно воспользоваться тем же методом, что и в задаче 2 к разделу 2. Тогда мы придём к выражениям вида (II.6,а-б), где давления Р заменены на константы k:
Подстановка даёт: при температуре Т3 константа скорости k3 ≈ 34∙105 1/с .
в) Теперь по ф-ле (17.10,б) нетрудно найти период полупревращения при данной температуре:
Как видно, термическое разложение этана происходит крайне быстро – по существу, в виде взрыва.
7. Пусть в реакции при температуре Т1 = 293 К 99%-ное разложение вещества А наступает через t99–1 = 2 часа. При какой температуре Т2 такая же степень разложения вещества А достигается уже за t99–2 = 15 мин.?
Видео:Кинетика || Лекция 4 || Реакции второго порядка, общий интеграл кинетического уравненияСкачать

Вычисления производить с помощью правила Вант-Гоффа. Температурный коэффициент реакции – γ = 3.
Видео:Лекция 5 || 2021 || Методы определения порядка реакции, сложные реакции (начало)Скачать

Решение
а) Период полупревращения (Т½) любого реагента обратно пропорционален константе скорости: это верно для реакций всех порядков – нулевого (17.4,б), первого (17.10,б), второго (17.27; 17.38) и третьего (17.44).
То же самое, очевидно, справедливо и для других времён – в частности, для t99 . Поэтому по отношению одноимённых времён при указанных температурах можно найти отношение констант скоростей:
б) Температурный коэффициент показывает, во сколько раз возрастает константа скорости реакции при повышении температуры на 10 градусов (18.27). В данном случае
в) Значит, если температура повысилась бы на 20 градусов, константа увеличилась бы в γ2 = 9 раз. У нас же рост константы составил 8 раз (IV.17). Следовательно, искомое повышение температуры – меньше 20 градусов.
г) Его находим из простейших соотношений:
8. Дана некая мономолекулярная реакция при температуре Т = 473 К. Её константа скорости при этой температуре – k = 62,8 1/c, а предэкспоненциальный множитель в уравнении Аррениуса – А = 2,5∙1013 1/c.
Найти теплоту активации (т. е. ΔН0ак) данной реакции при указанных условиях.
Видео:Механизмы реакций элиминирования (отщепление)Скачать

Решение
а) Из уравнения Аррениуса (18,22,а) выражаем энергию активации:
б) Теплоту же (энтальпию) активации находим из формулы (18.49):
Как видим, энергия активации по Аррениусу лишь немного отличается от энтальпии активации.
Начальные концентрации реагентов в растворе – с01 = с02 = 0.01 М, а затем концентрация щёлочи менялась следующим образом:
Видео:Лекция 6. Скорость химической реакцииСкачать

Необходимые исходные сведения и основные уравнения
Химическая кинетика – раздел физической химии изучающий закономерности протекания химической реакции во времени. В задачу этого раздела входит определение скорости и константы скорости химической реакции, а также изучение закономерностей их изменения в зависимости от различных факторов (температуры, давления, концентрации реагирующих веществ и др.).
Под скоростью химической реакции понимают изменение концентрации веществ в единицу времени. Для реакций, описываемых стехиометрическим уравнением
n 




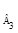
истинная скорость выражается
v = -dc 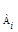

где 

где Dс i – изменение концентрации любого участника химичес-кой реакции за промежуток времени Dt. Зависимость скорости химической реакции от концентрации исходных веществ выражается законом действия масс (основной постулат химической кинетики):

где k – константа скорости химической реакции. Физический смысл константы скорости химической реакции заключается в том, что она численно равна скорости химической реакции в случае равенства единице (в молях на литр) концентрации всех реагирующих веществ. В химической кинетике различают также понятия «молекулярность» и «порядок реакции».
Молекулярность – это количество частиц, участвующих в элементарном акте химической реакции. Она может принимать любое целое положительное число. Однако вследствие малой вероятности одновременного столкновения большого количества частиц реакции с молекулярностью, превышающей четыре, практически не встречаются.
Порядок реакции – это сумма стехиометрических коэффициентов, стоящих перед символами химических веществ, участвующих в реакции, или сумма показателей степеней, с которыми концентрации веществ входят в основной постулат химической кинетики:
где n – порядок реакции.
Вследствие того, что запись химического уравнения не от-ражает механизма протекания реакции, в большинстве случаев порядок реакции не совпадает с суммой стехиометрических коэффициентов. Порядок реакции может принимать любое положительное значение, включая ноль и дробные числа. Порядок реакции необходим для правильного выбора кинети-ческого уравнения, позволяющего рассчитать скорость и константу скорости химической реакции.
Реакции нулевого порядка. В этих реакциях Sni = 0, следо-вательно, после объединения уравнений (3.1), (3.2) и (3.3) получаем
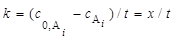
где c0, 
Реакции первого порядка. В этих реакциях Sn 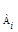
Реакции второго порядка. В этих реакциях Sn 
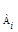


Во втором случае начальные концентрации реагирующих веществ не одинаковы
k=2,3 . t -1 (c0, 





Реакции n -го порядка. В этих реакциях Sn 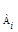
Под периодом полупревращения вещества t1/2 понимают промежуток времени, с, в течение которого прореагировала ровно половина первоначально взятого вещества. Период полураспада для разных реакций может принимать очень широкое значение: от долей секунды (радиоактивный распад большинства трансурановых элементов, взрывные реакции и др.) до миллионов лет (радиоактивный распад урана, окисление горных пород и др.). С учетом приведенного определения (c 

t1/2 = 
для реакций первого порядка
для реакций второго порядка
t1/2 = 
Определение порядка реакции методом Оствальда-Нойеса (интегральный метод):
где t’1/2 – период полураспада, соответствующий начальной концентрации реагирующего вещества c0,1; t»1/2 – период полураспада этого же вещества при другой начальной концентрации c0,2.
Определение порядка реакции методом Вант-Гоффа (дифференциальный метод):
где w1, w2 – средние скорости реакции, соответствующие начальным концентрациям с0,1 и с0,2.
Задачи с решениями
1. Вычислите константу скорости бимолекулярной реакции образования фосгена СО + С12 = СОС12, если при 27 о С количество реагирующих веществ изменяется следующим образом:
| Время, мин | 0 | 12 | 24 | 36 |
| Концентрация СО, моль/л | 0,01873 | 0,01794 | 0,011734 | 0,01674 |
Определите концентрацию исходных веществ через три часа после начала реакции.
Решение. Используем уравнение для расчета констант скоростей второго порядка, когда с1 = с2: k = t -1. ( c0,A -1 — . c0 -1 ). После подстановки в эту формулу данных из приведенной таблицы (любые три пары) получим: kср = 0,186 мин -1 . Рассчитаем концентрацию исходных веществ через три часа после начала реакции: 1,627 . х = 0,01174; х = 0,0072; а – х = 0,01873 — 0,00720 = = 0,0115.
Ответ: kср = 0,186 мин -1 ; [С12] = 0,0072 моль/л; [СО] = = 0,0015 моль/л.
2. Превращение пероксида бензоила в диэтиловый эфир (реакция 1-го порядка) прошло за 10 минут на 75,2%. Вычислите константу скорости реакции.
Решение Напишем уравнение для расчета константы скорости реакции первого порядка и подставим в него соответствующие значения: k = (2,303/t) . lg[a/(a —x)] = (2,303/10) х х lg(100/24,8) = 0,2303/0,606 = 0,140.
Ответ: k = 0,140 мин -1 .
3. Для химической реакции А ® В константа скорости k = = 0,5, исходная концентрация c0,А=1 моль/л. На основании этих данных определите степень превращения вещества А за время t = 1 ч, если реакция идет: а) по нулевому; б) первому; в) второму порядку. Как зависит степень превращения от порядка реакции?
Решение. Для реакции, протекающей по нулевому порядку, согласно уравнению (3.6): 0,5 = х/t; т. е. х = 0,5. Для реакции, протекающей по первому порядку, согласно уравнению (3.9): 0,5 = 2,3/1 . lg[1/(1-х)]; 0,5/2,3 = −lg(1-а); а = 0,39. Для реакции, протекающей по второму порядку, согласно уравнению (3.11): 0,5 = 1/1 . [1/(с0.(1-х)] – 1/с0); 0,5 = 1/(1-а); а = 0,33.
Ответ: Чем выше порядок, тем меньше степень превращения, тем медленнее идет реакция.
4. Период полураспада радиоактивного изотопа 14 С составляет 5730 лет. При археологических раскопках были найдены остатки дерева, содержание изотопа 14 С в котором составляло 72% от нормального. Определите возраст дерева.
Решение. Радиоактивный распад – реакция первого порядка. Константа скорости: k = 0,693/t1/2. Возраст дерева можно найти из решения кинетического уравнения с учетом того, что cА=0,72 . c0,А.Тогда: t =1/k . ln[A]0/[A] = (t1/2/ln2); ln([A]0/[A])= = (5730/ln(1/0,72))/ln2 = 2720.
Ответ: t = 2720 лет.
5. В некоторой реакции целого порядка nА ® В концентрация исходного вещества, равная 0,5 моль/л, была достигнута за 4 мин при начальной концентрации этого вещества 1 моль/л и за 5 мин при начальной концентрации 2 моль/л. Установите порядок реакции.
Решение. Из первого опыта следует, что период полураспада вещества при начальной концентрации 1 моль/л равен 4 мин. Во втором опыте при начальной концентрации 2 моль/л период полураспада равен 1 мин (переход от 2 до 0,5 моль/л прошел за 5 мин, из них от 1 до 0,5 моль/л – 4 мин, следовательно, переход от 2 до 1 моль/л потребовал 1 мин). Таким образом, при увеличении начальной концентрации в два раза период полураспада уменьшился в 4 = 2 n -1 раза, следовательно, порядок реакции n=3.
Ответ: Реакция 3-го порядка.
6. Для изучения разложения щавелевой кислоты в концентрированной серной кислоте приготовили 1/40 М раствор щавелевой кислоты в 99,5%-й серной кислоте. Через определенные промежутки времени из смеси отбирали пробы и определяли объем раствора перманганата калия, необходимый для титрования 10 мл раствора. Результаты эксперимента приведены ниже.
| t , мин | 0 | 120 | 240 | 420 | 600 | 900 | 1440 |
| V, мл | 11,45 | 9,63 | 8,11 | 6,22 | 4,79 | 2,97 | 1,44 |
Определите порядок реакции и ее константу скорости.
Решение. Данную задачу удобнее решить методом перебора кинетических уравнений для реакций различных порядков.
Предположим, что реакция имеет первый порядок. Кинетическим уравнением в этом случае является уравнение (3.8). После подстановки в это уравнение экспериментальных данных получим ряд констант скоростей: k = 0,00144; 0,00144; 0,00145; 0,00150; 0,00140.
Совпадение этих данных свидетельствует о правильном нашем предположении. В результате получаем вывод: эта реакция имеет первый порядок, а среднее значение ее константы скорости k = 0,00145 мин -1 .
Любое иное наше предположение о возможном другом порядке реакции после подстановки экспериментальных данных в соответствующие кинетические уравнения (3.6), (3.10), (3.12), (3.15) не приводит к удовлетворительному совпадению констант скоростей, рассчитанных с использованием полученных экспериментальных данных.
Ответ: Реакция первого порядка, k = 0,00145 мин -1 .
7. При взаимодействии брома с этиловым спиртом были получены следующие результаты:
| t, мин | 0 | 4 |
| c1, моль/л | 0,00814 | 0,00610 |
| c2, моль/л | 0,00424 | 0,00314 |
Определите порядок реакции по этим данным.
Решение. Определяем порядок реакции по методу Вант-Гоффа (3.17). Бесконечно малые приращения времени dt и убыли концентраций dс при определении скорости реакции заменяем на конечные приращения этих функций. В этом случае возможно применение уравнения (3.17) в виде n = [lg(Dс1/Dt) — — lg(Dс2/t)]/(lgс1 – lgс2).
Подставляем необходимые данные. Так как Dс/Dt = w, а скорость реакции средняя, то и концентрации с1и с2 также необходимо взять средние:
n = lg(0,00814-0,00610)/4 – lg(0,00424-0,00314)/4:
(lg0,00712 − 1g0,00369) = 0,91 » 1.
Следовательно, данная реакция является реакцией первого порядка.
Ответ: Реакция первого порядка.
3.3 Задачи для самостоятельного решения
1. В некоторый момент времени скорость сгорания циклогексана в избытке кислорода равна 0,350 моль/(л . с). Чему равны скорость образования СО2 и скорость расходования кислорода в этот момент?
2. В реакции второго порядка А + В ® 2D начальные концентрации веществ А и В равны друг другу (по 1,5 моль/л). Скорость реакции равна 2,0 . 0 -4 моль/(л . с) при [А]=1,0 моль/л. Рассчитайте константу скорости и скорость реакции при [В] = = 0,2 моль/л.
3. Разложение Н2О2 в спиртовом растворе – реакция первого порядка. Начальная скорость реакции при температуре 40 о С и концентрации Н2О2 0,156 М равна 1,14 . 10 -5 моль/(л . с). Рассчитайте константу скорости.
4. Реакция первого порядка протекает на 30% за 7 мин. Через какое время реакция завершится на 99%?
5. Период полураспада радиоактивного изотопа 137 Cs, который попал в атмосферу в результате Чернобыльской аварии, — 29,7 года. Через какое время количество этого изотопа составит менее 1% исходного?
6. Изотоп иод-131, который применяют для лечения некоторых опухолей, имеет период полураспада 8,1 суток. Какое время должно пройти, чтобы количество радиоактивного йода в организме больного уменьшилось в 100 раз?
7. Период полураспада радиоактивного изотоп 90 Sr, который попадает в атмосферу при ядерных испытаниях, − 28,1 года. Предположим, что организм новорожденного ребенка поглотил 1,00 мг этого изотопа. Сколько стронция останется в организме через: а) 18 лет, б) 70 лет, если считать, что он не выводится из организма?
8. Разложение иодоводорода HI(г) = ½ Н2(г) + ½ I2(г) на поверхности золота – реакция нулевого порядка. За 100 с концентрация йодоводорода уменьшилась с 0,335 М до 0,285 М. Рассчитайте константу скорости и период полураспада при начальной молярной концентрации йодоводорода 0,400 М.
9. Реакция второго порядка А + В ® Р проводится в растворе с начальными концентрациями [А]0 = 0,050 моль/л и [В]0 = = 0,080 моль/л. Через 1 ч концентрация вещества А уменьшилась до 0,020 моль/л. Рассчитайте константу скорости и периоды полураспада обоих веществ.
10. В некоторой реакции целого порядка nА ® В молярная концентрация исходного вещества 1,5 моль/л была достигнута за 5,0 мин при начальной концентрации 3,0 моль/л и за 6,25 мин при начальной концентрации 6,0 моль/л. Установите порядок реакции.
11. Было найдено, что при изменении начальной молярной концентрации с 0,502 до 1,007 моль/л период полураспада в некоторой реакции уменьшился с 51 до 26 с. Каков порядок этой реакции и чему равна константа скорости?
12. В течение часа подвергается распаду 1/16 часть неко-торого радиоактивного элемента. Определите период полу-распада этого элемента.
13. Концентрация атомов трития в воздухе приблизительно 5 . 10 -15 моль/л. Период полураспада трития около 12 лет. Через сколько лет распадается 90% трития, содержащегося в воздухе? Пополнение содержания трития в воздухе за счет реакций синтеза не учитывать.
14. Пероксид водорода в водном растворе разлагается по уравнению 2 Н2О2 ® 2 Н2О + О2. Кинетику этой реакции исследовали титрованием проб одинакового объема (2 мл) 0,015 М раствором перманганата калия. Определите порядок реакции всеми возможными способами и вычислите среднее значение константы скорости этой реакции, пользуясь приведенными данными:
| Время, мин | 0 | 5 | 10 | 15 | 20 | 30 | 40 |
| Количество KMnO4, мл | 23,6 | 18,1 | 14,8 | 12,1 | 9,4 | 5,8 | 3,7 |
15. При нагревании раствор дибромянтарной кислоты распадается на бромалеиновую кислоту и НВr по уравнению
СООН-СНBr-CHBr-COOH ® CHCOOH-CBrCOOH + HBr
При титровании раствора стандартным раствором щелочи через t , мин, титр ее в объеме раствора изменялся следующим образом:
| t , мин | 0 | 214 | 380 |
| Vщ, см 3 | 12,11 | 12,44 | 12,68 |
Вычислите константу скорости реакции. Через сколько времени разложится 1/3 дибромянтарной кислоты?
16. Бимолекулярная реакция, для которой сА=сВ, протекает за 10 мин на 25%. Сколько потребуется времени, чтобы реакция прошла на 50% при той же температуре?
17. При определенной температуре раствор уксусноэтилового эфира концентрации 0,01 моль/л омыляется раствором NaOH концентрации 0,002 моль/л на 10% за 23 мин. Через сколько минут он будет омылен до такой же степени раствором NaOH концентрации 0,005 моль/л если реакция омыления эфира – реакция второго порядка, а щелочь диссоциирована полностью?
18. Фенилдиазохлорид разлагается по уравнению C6H5N2CI= =C6H5CI + N2. При 323 К и начальной концентрации 10 г/л были получены следующие результаты:
| Время, мин | 6 | 9 | 12 | 14 | 22 | 24 | 26 | 30 | ¥ |
| Выделено N2, см 3 | 19,3 | 26,0 | 32,6 | 36,0 | 45,0 | 46,5 | 48,3 | 50,4 | 58,3 |
Определите порядок и константу скорости реакции.
19. Реакция разложения аммиака на горячей вольфрамовой проволоке протекает по стехиометрическому уравнению 2 NH3 = N2 + 3 H2. Во время реакции в различные моменты времени давление повышалось следующим образом:
| Время, с | 100 | 200 | 400 | 600 | 800 | 1000 |
| ΔР, Па | 1466,3 | 2945,9 | 5865,2 | 8837,8 | 11717,0 | 14663,0 |
Определите порядок реакции.
20.Окисление FeCl2 с помощью КС1О3 в присутствии НС1 – реакция третьего порядка. Если время выражать в минутах, а концентрации – в молях на литр, то константа скорости этой реакции равна приблизительно единице. Вычислите концентрацию FeCl2 через 1,5 ч после начала реакции, если начальные концентрации всех реагирующих веществ равны 0,2 моль/л.
🎦 Видео
Определение реакций опор в раме (жесткая заделка)Скачать
влияние концентрации реагирующих веществ на скорость химической реакцииСкачать
РАМА. Реакции в заделке. Сопромат.Скачать

3 1 Константа химической реакцииСкачать

Определение реакций опор простой рамыСкачать

Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Определение реакций опор в балке. Сопромат.Скачать



