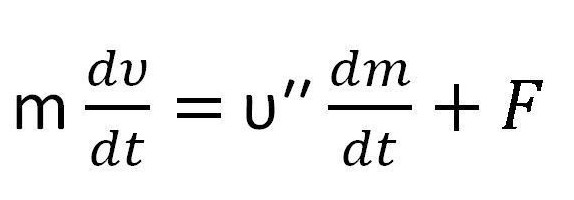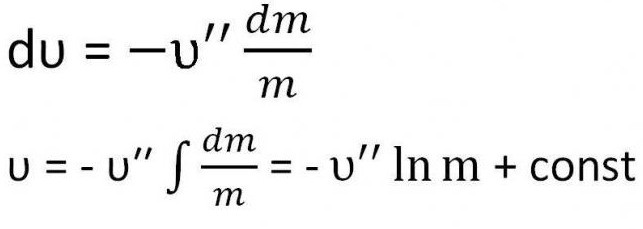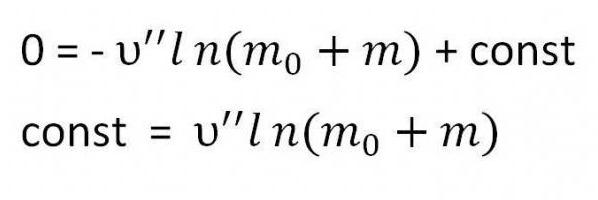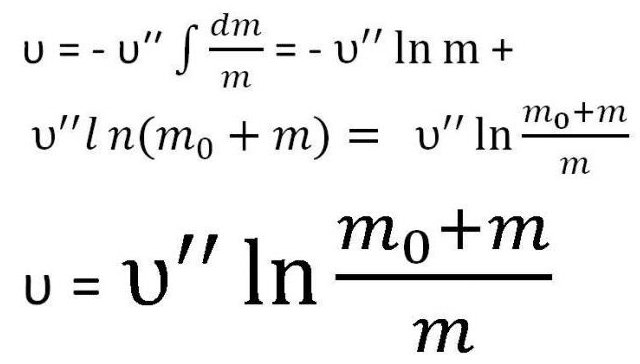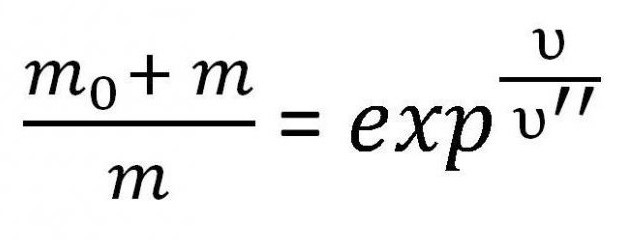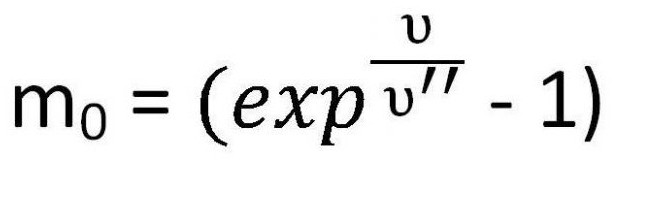Реактивное движение уравнение мещерского циолковского

Формула Константина Эдуардовича Циолковского выражает максимальную скорость летательного аппарата, которой он достигает во время полета при реактивном движении. Она получается при интегрировании уравнения Мещерского.

Видео:Урок 106. Реактивное движениеСкачать

Формула Циолковского

Эта формула выражает скорость ракеты, переданную газами от сожженного топлива. Уравнение Мещерского и формула Циолковского неразрывно связаны — уравнение Мещерского описывает массу материальной точки, которая изменяется со временем, в то время как при реактивном движении ракеты постоянно идет уменьшение ее массы из-за сгорания топлива. Изменение скорости при изменяющейся массе (уменьшающейся в нашем случае) движущегося тела — вот что подразумевает под собой реактивное движение. Формула Циолковского основывается именно на нем.

Для решения ряда задач теоретической механики в области реактивного движения используют уравнение Мещерского (основное уравнение материальной точки переменной массы) и формулу Циолковского (формула конечной скорости летательного аппарата), которые называются основными соотношениям теории реактивного движения.

Основой при проектировании и планировании в области космических полетов является именно формула Циолковского, вывод которой стал настоящим прорывом для освоения космоса.

Видео:Уравнение Мещерского, формула ЦиолковскогоСкачать

Задачи Циолковского

Для того, чтобы разрешить проблему межпланетных перелетов, К. Э. Циолковский рассмотрел в качестве средства перелета ракету. Он вывел формулу, с помощью которой можно получить зависимость массы летательного аппарата с топливом и скорости отдаления продуктов сгорания используемого топлива ракеты относительно нее. Покажем две его задачи:

• Исследование движения тела с переменной массы с действующей на него одной реактивной силы.
• Исследование движение тела в однородном поле силы тяжести переменной массы вблизи поверхности Земли.

Видео:Формула ЦиолковскогоСкачать

Предисловие

Для всех космических полетов изначальной и основополагающей стала формула Циолковского для скорости ракеты, вывод которой представлен ниже.

Для начала необходимо приняв ее, грубо говоря, за материальную точку. На нее будут действовать силы притяжения Земли и других небесных тел (в момент взлета сила гравитации Земли будет, конечно же, наиболее сильной), сила сопротивления воздуха с одной стороны и противоположно им направленная реактивная сила, возникающая из-за выброса сгоревшего газа у основания тела. Ракета с большой силой выбрасывает эти газы, которые сообщают ей ускорение, направленное противоположно стороне выброса. Теперь необходимо представить эти рассуждения в виде формулы.

Сам принцип полета ракеты достаточно простой. С большой скоростью из ракеты вырывается газ, полученный при сгорании топлива, который сообщает самой ракете определенную силу, которая действует противоположно направлению движения. Так как считается, что внешние силы не действуют на ракету, то система будет замкнутой, и импульс ее не зависит от времени.

Видео:Уравнение Мещерского и формула Циолковского LIVE | 11 класс, студенты МФТИ | Вузовская физика с FСкачать

Уравнение Мещерского

Одним из основных примеров движения тела с изменяющейся массой является ракета с одной ступень, масса которой изменяется только из-за сжигания топлива, содержащегося в ней. Масса такой ракеты складывается из неизменяющейся (сама ракета и ее полезная нагрузка) и изменяющейся (топливо). Такой пример является упрощенной моделью.

Однако в современном ракетостроении используются многоступенчатые ракеты. Принцип их работы заключается в том, что благодаря большому объему ступеней они способны перевозить и использовать после взлета гораздо большее количество топлива. После его сгорания, ракете сообщается значительный импульс (гораздо больший, чем тот, которого можно добиться, используя одну ступень), а ставшие ненужными части открепляются от основы, уменьшая общий вес на 80-90%. Тем не менее, для расчета параметров многоступенчатой ракеты необходимо сложить показатели каждой из ее составляющей.

Дифференциальное уравнение Мещерского описывает движение материальной точки с переменной массой.

(m+dm)(υ+dυ) + dm′ υ′ — mυ = Fdt — в момент времени dt (разность между силой в момент времени t и dt+t и будет приращением).

Где m и υ зависят от времени, dt — какое-то время полета. За его образуется сила перемещения газа — dm′ υ′, dm′ — масса образованного из топлива газа. F — равнодействующая сила.

В описанном выше выражении приращения массы ракеты и газа и скорости устремляется к нулю, поэтому выражение принимает следующий вид:

причем υ′′ равняется разности скорости газа и скорости и является скоростью истечения газа.

Оно и называется уравнением Мещерского.

Видео:Реактивное движение. Ф-ла МещерскогоСкачать

Вывод формулы Циолковского

Необходимо вывести формулу, описывающую движение тела с переменной массой. Формула Циолковского таковой и является. Вывод представлен ниже.

В данных вычислениях считается, что на движущееся тело не действуют внешние силы, то есть F = 0.

Так как воздействие внешних сил на летящую ракету равно нулю, то она движется прямолинейно, а скорость движения противоположно направлена скорости выхода газа. Соответственно, υ = -υ′′

Получается выражение, которое необходимо проинтегрировать.

Необходимо найти константу. Для этого достаточно подставить в уравнение начальные условия — скорость равна нулю, а масса — сумме массы топлива и массы ракеты (m₀ + m)

Вообще говоря, m в формуле складывается из двух параметров — из полезной нагрузки и конструкции ракеты. Полезной нагрузкой называется общая масса груза и экипажа.

Подставляем найденную константу в формулу. В результате и получается выражение искомой формулы.

Это и есть один из вариантов формулы Циолковского для скорости. Однако иногда необходимо принять во внимание именно массу. Поэтому ее иногда записывают следующим образом:

Данная формула используется для расчета массы топлива, которая требуется для развития определенной скорости при заданных условиях.

Рассмотрю далее небольшую задачу. Предположим, ракете необходимо развить первую космическую скорость для вращения по орбите Земли. Тогда для этого необходимо в первую очередь рассчитать массу топлива, конечно же. Тогда ее очень просто выразить из формулы Циолковского.

Видео:Механика Л8. 2022. Уравнение Мещерского. Формула Циолковского. Проблема Лапласовского детерминизмаСкачать

Релятивистская механика

Все вышеописанные формулы могут применяться только в том случае, когда скорость ракеты много меньше скорости света (υ

Видео:Главная формула космонавтики. Формула Циолковского | Море ЯсностиСкачать

§ 5.4. Реактивное движение. Уравнение Мещерского. Реактивная сила

Какое движение называется реактивным?

Под реактивным движением понимают движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно тела, например при истечении продуктов сгорания из сопла реактивного летательного аппарата. При этом появляется так называемая реактивная сила, сообщающая телу ускорение.

Наблюдать реактивное движение очень просто. Надуйте детский резиновый шарик и отпустите его. Шарик стремительно взовьется вверх (рис. 5.4). Движение, правда, будет кратковременным. Реактивная сила действует лишь до тех пор, пока продолжается истечение воздуха.

Главная особенность реактивной силы состоит в том, что она возникает без какого-либо взаимодействия с внешними телами. Происходит лишь взаимодействие между ракетой и вытекающей из нее струей вещества.

Сила же, сообщающая ускорение автомобилю или пешеходу на земле, пароходу на воде или винтовому самолету в воздухе, возникает только за счет взаимодействия этих тел с землей, водой или воздухом.

При истечении продуктов сгорания топлива они за счет давления в камере сгорания приобретают некоторую скорость относительно ракеты и, следовательно, некоторый импульс. Поэтому в соответствии с законом сохранения импульса сама ракета получает такой же по модулю импульс, но направленный в противоположную сторону.

Масса ракеты с течением времени убывает. Ракета в полете является телом переменной массы. Для расчета ее движения удобно применить закон сохранения импульса.

Уравнение Мещерского

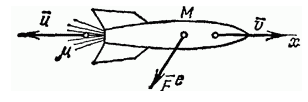
Выведем уравнение движения ракеты и найдем выражение для реактивной силы. Будем считать, что скорость вытекающих из ракеты газов относительно ракеты постоянна и равна . Внешние силы на ракету не действуют: она находится в космическом пространстве вдали от звезд и планет.

Пусть в некоторый момент времени скорость ракеты относительно инерциальной системы, связанной со звездами, равна (рис. 5.5, а), а масса ракеты равна М. Через малый интервал времени Δt масса ракеты станет равной

где μ — расход топлива(1).

За этот лее промежуток времени скорость ракеты изменится на Δ и станет равной ₁ = + Δ. Скорость истечения газов относительно выбранной инерциальной системы отсчета равна + (рис. 5.5,б), так как до начала сгорания топливо имело ту же скорость, что и ракета.

Запишем закон сохранения импульса для системы ракета — газ:

Раскрыв скобки, получим:

Слагаемым μΔtΔ можно пренебречь по сравнению с остальными, так как оно содержит произведение двух малых величин (это величина, как говорят, второго порядка малости). После приведения подобных членов будем иметь:

Это одно из уравнений Мещерского(2) для движения тела переменной массы, полученное им в 1897 г.

Если ввести обозначение _р = -μ, то уравнение (5.4.1) совпадет по форме записи со вторым законом Ньютона. Однако масса тела М здесь не постоянна, а убывает со временем из-за потери вещества.

Величина _р = -μ носит название реактивной силы. Она появляется вследствие истечения газов из ракеты, приложена к ракете и направлена противоположно скорости газов относительно ракеты. Реактивная сила определяется лишь скоростью истечения газов относительно ракеты и расходом топлива. Существенно, что она не зависит от деталей устройства двигателя. Важно лишь, чтобы двигатель обеспечивал истечение газов из ракеты со скоростью при расходе топлива μ. Реактивная сила космических ракет достигает 1000 кН.

Если на ракету действуют внешние силы, то ее движение определяется реактивной силой и суммой внешних сил. В этом случае уравнение (5.4.1) запишется так:

Принцип реактивного движения основан на том, что истекающие из реактивного двигателя газы получают импульс. Такой же по модулю импульс приобретает ракета.

Вопросы для самопроверки

1. Реактивное движение совершает кальмар (рис. 5.6). Как это ему удается?

Рис. 5.6

(1) Расходом топлива называется отношение массы сгоревшего топлива ко времени его сгорания.

(2) Мещерский И. В. (1859—1935) — профессор Петербургского политехнического института. Его труды по механике тел переменной массы стали теоретической основой ракетной техники.

Видео:Механика | динамика | основы реактивного движения | 2 | уравнение Мещерского | для взрослыхСкачать

Движение тела с переменной массой

Для начала сформулируем, что такое переменная масса.

Переменная масса – это масса тела, которая может меняться при медленных движениях из-за частичных приобретений или потерь составляющего вещества.

Видео:Александр Сенкевич — Двигатели для полетов в глубокий космосСкачать

Уравнение движения материальной точки с переменной массой

Чтобы записать уравнение движения для тела с такой массой, возьмем для примера движение ракеты. В основе ее перемещений лежит очень простой принцип: она движется за счет выброса вещества с большой скоростью, а также сильного воздействия, оказываемого на это вещество. В свою очередь выбрасываемые газы также оказывают воздействие на ракету, придавая ей ускорение в противоположном направлении. Кроме того, ракета находится под действием внешних сил, таких, как гравитация Солнца и других планет, земная тяжесть, сопротивление среды, в которой она совершает движение.

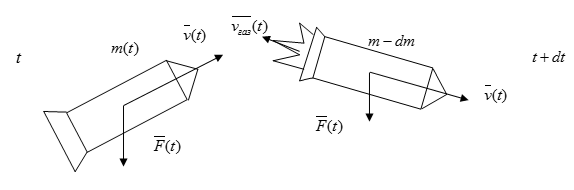
Обозначим массу ракеты в какой-либо момент времени t как m ( t ) , а ее скорость как v ( t ) . То количество движения, которая она при этом совершает, будет равно m v . После того, как пройдет время d t , обе эти величины получат приращение (соответственно d m и d v , причем значение d m будет меньше 0 ). Тогда количество движения, совершаемого ракетой, станет равно:

( m + d m ) ( v + d v ) .

Нам необходимо учитывать тот момент, что за время d t также происходит движение газов. Это количество тоже нужно добавить в формулу. Оно будет равно d m г а з v г а з . Первый показатель означает массу газов, которые образуются за указанное время, а второй – их скорость.

Теперь нам нужно найти разность между суммарным количеством движения за время t + d t и количеством движения системы во время t . Так мы найдем приращение данной величины за время d t , которое будет равно F d t (буквой F обозначена геометрическая сумма всех тех внешних сил, которые действуют в это время на ракету).

В итоге мы можем записать следующее:

( m + d m ) ( v + d v ) + d m г а з + v г а з — m v = F d t .

Поскольку нам важны именно предельные значения d m d t , d v d t и их производные, приравняем эти показатели к нулю. Значит, после раскрытия скобок произведение d m · d v может быть отброшено. С учетом сохранения массы получим:

d m + d m г а з = 0 .

Теперь исключим массу газов d m г а з и получим скорость, с которой газы будут покидать ракету (скорость струи вещества), выражающаяся разностью v о т н = v г а з — v . Учитывая эти преобразования, можно переписать исходное уравнение в следующем виде:

d m v = v о т н d m + F d t .

Теперь разделим его на d t и получим:

m d v d t = v о т н d m d t + F .

Видео:3.4. Реактивное движение | Динамика | Александр Чирцов | ЛекториумСкачать

Уравнение Мещерского

Форма полученного уравнения точно такая же, как у уравнения, выражающего второй закон Ньютона. Но, если там мы имеем дело с постоянной массой тела, то здесь из-за потери вещества она постепенно меняется. К тому же помимо внешней силы нужно учитывать так называемую реактивную силу. В примере с ракетой это будет сила выходящей из нее газовой струи.

Уравнение m d v d t = v о т н d m d t + F впервые вывел русский механик И.В. Мещерский, поэтому оно получило его имя. Также его называют уравнением движения тела с переменной массой.

Видео:Формула ЦиолковскогоСкачать

Формула Циолковского

Попробуем исключить из уравнения движения ракеты внешние силы, воздействующие на нее. Предположим, что движение ракеты прямолинейно, а направление противоположно скорости газовой струи v о т н . Будем считать направление полета положительным, тогда проекция вектора v о т н является отрицательной. Она будет равна — v о т н . Переведем предыдущее уравнение в скалярную форму:

m d v = v о т н d m .

Тогда равенство примет вид:

d v d m = — v о т н m .

Газовая струя может выходить во время полета с переменной скоростью. Проще всего, разумеется, принять ее в качестве константы. Такой случай наиболее важен для нас, поскольку так уравнение решить намного проще.

Исходя из начальных условий, определим, какое значение приобретет постоянная интегрирования С. Допустим, что в начале пути скорость ракеты будет равна 0 , а масса m 0 . Следовательно, из предыдущего уравнения можем вывести:

C = v о т н ln m 0 m .

Тогда мы получим соотношения следующего вида:

v = v о т н ln m 0 m или m 0 m = e v v о т н .

Это соотношение и является формулой Циолковского.

Она предназначена для расчета запаса топлива, с помощью которого ракета может набрать необходимую скорость. При этом время сгорания топлива не обусловливает величину максимальной скорости ракеты. Чтобы разогнаться до предела, нужно увеличить скорость истечения газов. Для достижения первой космической скорости следует изменить конструкцию ракеты. Она должна быть многоступенчатой, поскольку необходимо меньшее соотношение между требуемой массой топлива и массой ракеты.

Разберем несколько примеров применения данных построений на практике.

Условие: у нас есть космический корабль, скорость которого постоянна. Для изменения направления полета в ней нужно включить двигатель, который выбрасывает газовую струю со скоростью v о т н . Направление выброса перпендикулярно траектории корабля. Определите угол изменения вектора скорости при начальной массе корабля m 0 и конечной m .

Решение

Ускорение по абсолютной величине будет равно a = ω 2 r = ω v , причем v = c o n s t .

Значит, уравнение движения будет выглядеть так:

m d v d t = v о т н d m d t перейдет в m v ω d t = — v о т н d m .

Поскольку d a = ω d t является углом поворота за время d t , то после интеграции первоначального уравнения получим:

a = v о т н v ln m 0 m .

Ответ: искомый угол будет равен a = v о т н v ln m 0 m .

Условие: масса ракеты перед стартом равна 250 к г . Вычислите высоту, которую она наберет через 20 секунд после начала работы двигателя. Известно, что топливо расходуется со скоростью 4 к г / с , а скорость истечения газов постоянна и равна 1500 м / с . Поле тяготения Земли можно считать однородным.

Решение

Начнем с записи уравнения Мещерского. Оно будет иметь следующий вид:

m ∆ v 0 ∆ t = μ v о т н — m g .

Здесь m = m 0 — μ t и v 0 – скорость ракеты в заданный момент времени. Разделим переменные:

∆ v 0 = μ v о т н m 0 — μ t — g ∆ t .

Теперь решим полученное уравнение с учетом первоначальных условий:

v 0 = v о т н ln m 0 m 0 — μ t — g t .

С учетом того, что H 0 = 0 при t = 0 , у нас получится:

H = v о т н t — g t 2 2 + v о т н m 0 μ 1 — μ t m 0 ln 1 — μ t m 0 .

Добавим заданные значения и найдем ответ:

H = v о т н t — g t 2 2 + v о т н m 0 μ 1 — μ t m 0 ln 1 — μ t m 0 = 3177 , 5 м .

Ответ: через 20 секунд высота ракеты будет составлять 3177 , 5 м .

🔥 Видео

Физика 10 класс (Урок№12 - Реактивное движение.)Скачать

Закон сохранения импульса. Практическая часть - решение задачи. 9 класс.Скачать

6.1. Реактивное движение. Уравнение Мещерского. Повозка Ньютона.Скачать

8. Движение тел с переменной массойСкачать

Формула ЦиолковскогоСкачать

Механика. Л 8.1. Мощность. КПД. Уравнение Мещерского. Уравнение Бернулли.Скачать

Реактивное движение. Ракеты | Физика 9 класс #21 | ИнфоурокСкачать

Консультация к устному экзамену. Механика. Часть 2: "Движение систем"Скачать

Дифференциальные уравнения 3. Формула ЦиолковскогоСкачать