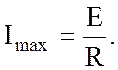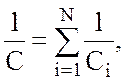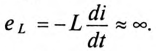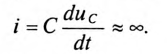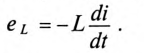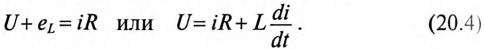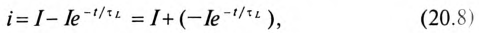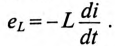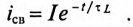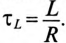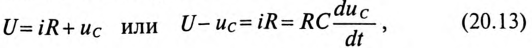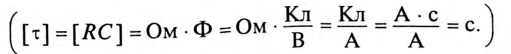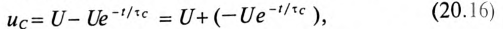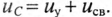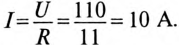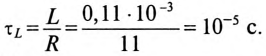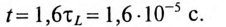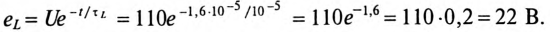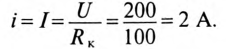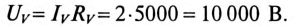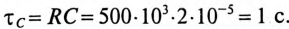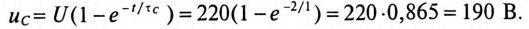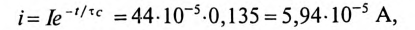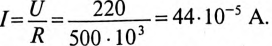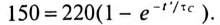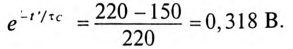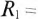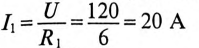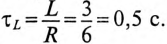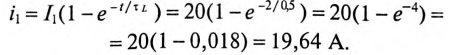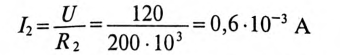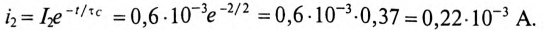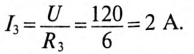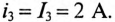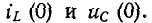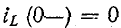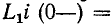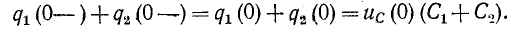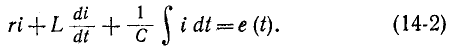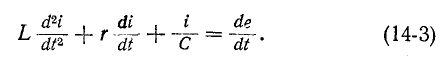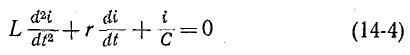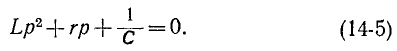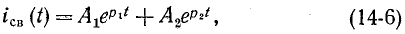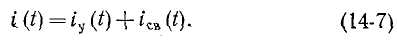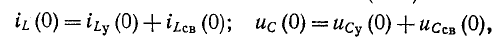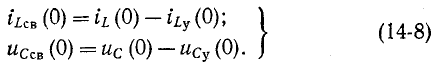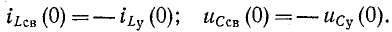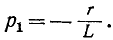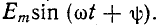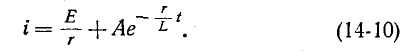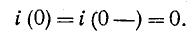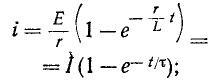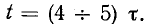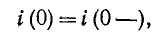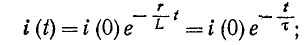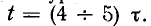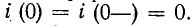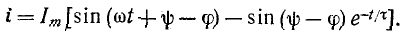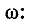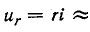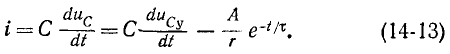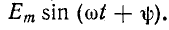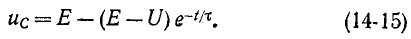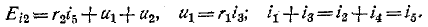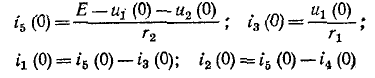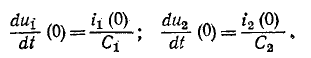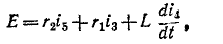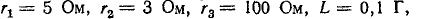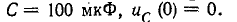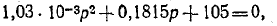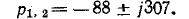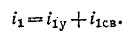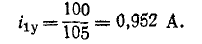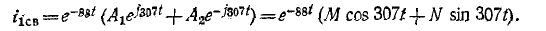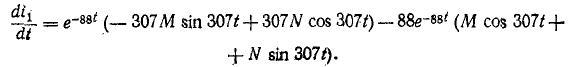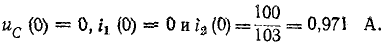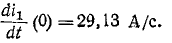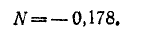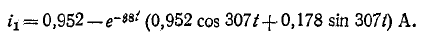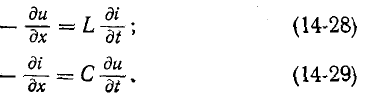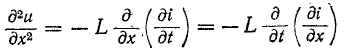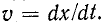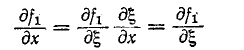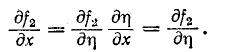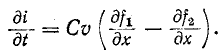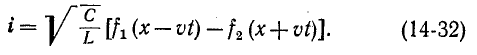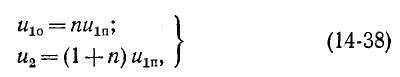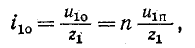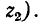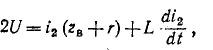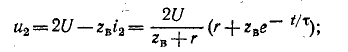- Страницы работы
- Содержание работы
- Лабораторная работа №8
- ИЗУЧЕНИЕ ПРОЦЕССОВ ЗАРЯДКИ И РАЗРЯДКИ КОНДЕНСАТОРА
- ЭС.2. исследование процессов установления тока и напряжения в электрической цепи при зарядке и разрядке конденсатора
- ЭКСПЕРИМЕНТАЛЬНОЯ ЧАСТЬ
- Переходные процессы в электрических цепях
- Переходный процесс в электрической цепи
- Подключение катушки индуктивности к источнику с постоянным напряжением
- Отключение и замыкание RL-цепи
- Зарядка, разрядка и саморазрядка конденсатора
- Переходные процессы в электрических цепях. Классический метод расчета
- Законы коммутации и начальные условия
- Установившийся и свободный режимы
- Переходный процесс в цепи r, L
- Переходный процесс в цепи r, С
- Включение в цепь r, С постоянной э. д. с.
- Переходные процессы в цепях с распределенными параметрами
- 💡 Видео
Страницы работы
Содержание работы
Видео:Конденсаторы. Процессы заряда и разряда конденсатораСкачать

Лабораторная работа №8
Видео:Разрядка конденсатора.Скачать

ИЗУЧЕНИЕ ПРОЦЕССОВ ЗАРЯДКИ И РАЗРЯДКИ КОНДЕНСАТОРА
Цель: усвоение понятия электрической емкости, изучение процессов зарядки и разрядки конденсатора осциллографическим методом, определение времени релаксации процесса и емкости конденсатора.

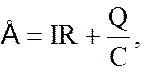
согласно которому сторонняя ЭДС равна сумме падений напряжения на всех участках цепи (внутренним сопротивлением источника пренебрегаем). В выражении (8.1) учтено, что напряжение Uc на обкладках конденсатора связано с зарядом Q соотношением Uc = Q/C , где С – емкость конденсатора. Дифференцируя (8.1) по времени и принимая во внимание, что сила тока равна скорости изменения заряда на обкладках
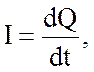 |
получаем дифференциальное уравнение с разделяющимися переменными
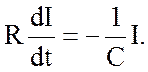 |
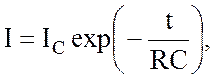
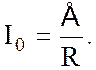
При разрядке конденсатора соответственно справедливы соотношения
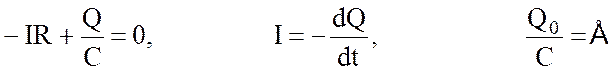 |
(направление тока изменилось на противоположное, происходит уменьшение заряда на обкладках, начальное напряжение на конденсаторе равно ЭДС источника). В результате зависимость силы тока от времени остается неизменной.
Из уравнения (8.3) находим закон изменения напряжения UR на сопротивлении R и напряжения на конденсаторе UC (рис 8.2):
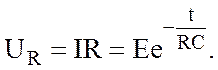 |
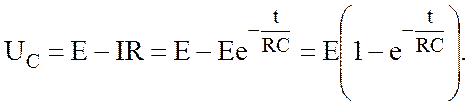 |
 |
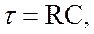
в течение которого сила тока уменьшается в е раз, т.е. при t = t составляет 0,368 от максимального значения
Закон изменения тока I и напряжений UR и UC при разрядке конденсатора через сопротивление R при отключенной ЭДС. Е находится из уравнения UС = IR. Студентам самим предоставляется возможность выполнить решение этой задачи и убедиться в том, что UС , I и UR при разрядке конденсатора изменяются по одному и тому же закону:
exp(-t/RC). Если прологарифмировать выражение (8.3), получаем:
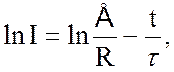 |
то есть изменение логарифма силы тока прямо пропорционально времени. При этом угловой коэффициент прямой, графически выражающий зависимость ln I =f(t), связан со временем релаксации обратной зависимостью
tg a = 1/t. Точка пересечения прямой с осью ординат дает значение логарифма начальной силы тока (рис 8.3).
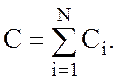
В случае последовательного соединения конденсаторов справедлива такая же формула, как при параллельном соединении резисторов:
где N – количество соединенных конденсаторов.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ.
Кассета ФПЭ–ПИ/09, магазин сопротивлений (2шт), магазин емкостей, источник питания, генератор низкочастотный, осциллограф С1-117.
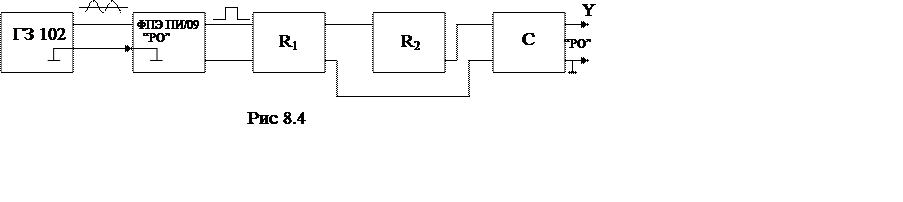 |
Работа выполняется по схеме, приведенной на рис 8.4.
С низкочастотного генератора синусоидальный сигнал подается на кассету ПИ, с выхода которой прямоугольные импульсы через два магазина сопротивлений подаются на магазин емкостей. Для того, чтобы получить осциллограммы зарядки и разрядки конденсатора, необходимо через постоянные промежутки времени подключать конденсатор к цепи и сразу же его отключать. При чем частота переключения должна быть такой, при которой незаметно было бы мерцание изображения на экране. Роль такого переключателя в данной работе выполняют прямоугольные импульсы, получаемые с помощью кассеты ФПЭ–ПИ/09 или непосредственно с выхода генератора, поскольку большинство генераторов имеют синусоидальный и прямоугольный выходной сигналы.
Синусоидальный сигнал (1-3)В подается от входных гнезд Х1, Х2 через разделительный конденсатор С1 на компоратор напряжения (микросхема серии К554СА3Б). Выходной сигнал компоратора управляется усилительным каскадом. С выходных гнезд Х3, Х4 снимается сигнал прямоугольной формы положительной полярности, амплитудой 11,5 В при нажатой кнопке S 2.2. При нажатии кнопки S 2.1 переключателя S2 (см переднюю панель кассеты ФПЭ–ПИ/09) на выходе получаем сигнал синусоидальной формы. К кнопке S 2.3 подпаян диод, препятствующий разряду емкости через преобразователь импульсов в период паузы. Плавное изменение скважности осуществляется изменением активного сопротивления потенциометром R1, глубокая регулировка скважности осуществляется при помощи кнопочного переключателя S1, установленного на передней панели. Этим переключателем можно менять емкость цепочки, подключив один конденсатор С2 или оба сразу С2 и С3.
1. Используя рис 8.4 соберите рабочую схему. Подключите к разъему кассеты ФПЭ–ПИ/09 кабель источника питания.
Внимание: без кассеты ПИ/09 можно получить прямоугольный сигнал непосредственно с генератора.
2. При трех различных значениях t = R2C получите на экране осциллографа изображение импульсов зарядки и разрядки конденсатора. С помощью ручек «Вольт/делен», «синхронизация», и «время/делен» добейтесь устойчивого неподвижного изображения зарядки и разрядки конденсатора.
3. Зарисуйте координатную сетку экрана осциллографа в масштабе и кривые импульсов. Определите для всех трех значений время релаксации t (см рис 8.2, б), емкость конденсатора по известному сопротивлению и максимальное напряжение в импульсе. Вычислите постоянную времени цепи t расчетным путем и сравните ее со значением, найденным экспериментально. Найдите среднюю арифметическую ошибку измерений.
4. Не изменяя параметров схемы, подключите вход «Y» осциллографа к выходу сопротивления R1 и зарисуйте осциллограмму напряжения UR (см рис 8.2, б).
1. Квазистационарные токи.
2. Дифференциальные уравнения для RC – цепи.
3. Зависимость тока зарядки и разрядки конденсатора от времени.
4. Определение t цепи из осциллограммы.
5. Расчет емкости при параллельном и последовательном соединении конденсаторов.
6. В цепи, состоящей из последовательно соединенных С = 0,3 мкФ, R = 20 кОм, Е = 12 В, определить:
а) постоянную времени,
б) максимальный заряд, приобретенный конденсатором,
в) время, через которое заряд достигнет 90% от максимального.
Видео:Как правильно разрядить конденсаторСкачать

ЭС.2. исследование процессов установления тока и напряжения в электрической цепи при зарядке и разрядке конденсатора
ТОКА И НАПРЯЖЕНИЯ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
ПРИ ЗАРЯДКЕ И РАЗРЯДКЕ КОНДЕНСАТОРА
ЦЕЛЬ РАБОТЫ: исследование процессов, протекающих в электрической цепи, обладающей емкостью и сопротивлением.
Если сообщить уединенному проводнику электрический заряд q,
то его потенциал j будет возрастать пропорционально заряду:

Коэффициент С называется электроемкостью уединенного проводника. Выясним физический смысл этой величины.
Если заряд проводника увеличить на Dq, то потенциал увеличится на Dj, причем в силу формулы (1) 
Отсюда 
Уединенные проводники обычных размеров обладают небольшой электроемкостью. А на практике нужны устройства, которые при небольшом (относительно окружающих тел) потенциале накапливали бы на себе большие заряды. Такие устройства называются конденсаторами. Конденсатор состоит их двух проводников, называемых обкладками, которые разделены прослойкой диэлектрика.
Под электроемкостью конденсатора понимают взаимную электроемкость его обкладок, т. е. это есть величина, численно равная заряду Dq, который нужно перенести с одной обкладки на другую для того, чтобы изменить разность потенциалов между ними 

Электроемкость конденсатора зависит от формы, размеров и взаимного расположения обкладок, а также от диэлектрической проницаемости диэлектрика, разделяющего обкладки. Если приложить к конденсатору некоторую разность 
Найдем электроемкость такого конденсатора. Перенесем с положительно заряженной обкладки 1 весь заряд на отрицательно заряженную обкладку 2 (после этого заряды обкладок будут равны нулю). При этом разность потенциалов между обкладками изменяется от начального значения 
Итак, мы перенесли с одной обкладки на другую заряд Dq = +q, при этом разность потенциалов между обкладками изменилась на DU = U. Тогда в силу формулы (2)

т. е. электроемкость конденсатора равна отношению заряда положительно заряженной обкладки к разности потенциалов между положительно и отрицательно заряженными обкладками.
Для того, чтобы электроемкость конденсаторов была больше, используют диэлектрики с большой диэлектрической проницаемостью. Для того, чтобы электроемкость не зависела от тел, расположенных вблизи конденсатора, форма, размеры и расположение обкладок должны быть такими, чтобы электрическое поле конденсатора было в основном сосредоточено между обкладками.
В электрических цепях наличие конденсаторов существенно влияет на протекание процессов, поскольку конденсаторы обладают способностью накапливать заряды и энергию. При включении или выключении источника питания в цепи, обладающей емкостью и сопротивлением, протекают переходные процессы, т. е. процессы установления стационарных (неизменных) значений силы тока и напряжений на отдельных элементах цепи.
Рассмотрим процессы установления тока и напряжения в цепи при заряде и разряде конденсатора.
На рис.2 показана цепь, состоящая из последовательно соединенных конденсатора С и резистора R. Предположим, что конденсатор заряжен так, что его обкладки обладают зарядами +q и -q, разность потенциалов между обкладками равна Uo. Электрическое поле, сосредоточенное в пространстве между обкладками, обладает энергией

Замкнем ключ К в положение 1. Тогда по цепи пойдет ток: положительные заряды с верхней обкладки будут перемещаться по проводникам на нижнюю.
При этом разность потенциалов между обкладками будет уменьшаться, а следовательно (в силу закона Ома), будет уменьшаться ток в цепи. Энергия электрического поля конденсатора (4) идет на нагревание резистора R. Ток в цепи будет течь до тех пор, пока вся энергия (4) не будет израсходована на нагревание.
Рассмотрим процесс разряда конденсатора количественно.
Пусть I, q, U – мгновенные значения тока, заряда положительной обкладки и разности потенциалов между обкладками. Считая ток в проводе положительным, когда он течет от положительно заряженной обкладки к отрицательно заряженной, можем записать:



где знак минус отражает факт уменьшения заряда (конденсатор разряжается). Исключая U и I, получим:
После интегрирования этого уравнения придем к соотношению

где qo – начальное значение заряда конденсатора; t – время, в течение которого заряд конденсатора убывает в e раз.
Оно называется временем релаксации: t = RC.
Дифференцируя (6) по t, находим закон изменения тока во времени:

где 
В соответствии с определением электроемкости имеем q = CU, откуда получаем закон изменения разности потенциалов во времени:


Предположим, что конденсатор С полностью заряжен. Замкнем ключ К в положение 2. В цепи будет проходить переходный процесс, который заключается в заряде конденсатора С через резистор R. Источник e возбуждает ток, заряжающий конденсатор, однако заряды на обкладках конденсатора препятствуют дальнейшей зарядке конденсатора, тем самым ограничивают прохождение тока и уменьшают его. Уравнения в этом случае имеют вид:



Исключая I и U, придем к уравнению
Это неоднородное дифференциальное уравнение можно свести к однородному, сделав замену 
Решение этого уравнения известно:
В начальный момент времени конденсатор не заряжен, т. е. в этот момент q = 0. Это дает 
При 

Для тока, продифференцировав, получаем

где 
По аналогии с разрядкой конденсатора для разности потенциалов получаем

Зависимости силы тока и разности потенциалов при зарядке и разрядке конденсатора носит экспоненциальную зависимость, которая определяется величиной параметра tтеор= RC (рис.3).
Это произведение имеет размерность времени. Из дифференциальных уравнений видно, что время релаксации t есть величина обратная скорости изменения заряда на обкладках конденсатора.
Отсюда следует, что чем больше t, тем медленнее будет уменьшаться с течением времени множитель 
Таким образом, постоянная времени t характеризует длительность переходных процессов, происходящих в цепи. За время t=t заряд конденсатора либо уменьшается в e раз при разрядке конденсатора, либо достигает значения в e раз меньшего, чем максимальное q0 при его зарядке.
Имея экспоненциальные кривые напряжения или тока, можно найти постоянную времени цепи tэксп. Для этого на графике U(t) или I(t) при разрядке и зарядке выбирают уровень 


Исследование переходных процессов при зарядке и разрядке конденсаторов, построение экспоненциальных кривых, определение постоянной времени и является целью данной лабораторной работы.
Для проверки экспоненциальной зависимости и определения времени релаксации используют другой метод. Если прологарифмировать (8) и (12), то получим зависимости типа:


Построив графики зависимости 


Видео:Зарядка и разрядка конденсаторовСкачать

ЭКСПЕРИМЕНТАЛЬНОЯ ЧАСТЬ
1. Собрать схему.
2. На пульте переключатель «U-0-I» поставить в
положение «0» (в середине).
3. На источнике питания включить тумблер «Сеть». Переключатель напряжения установить в правое положение «0-36 В».
4. На вольтметре В7-18 соединительный кабель вставить в гнездо «U
Видео:Зарядка конденсатора в электрической цепиСкачать

Переходные процессы в электрических цепях
Содержание:
Переходные процессы в электрических цепях:
Переходный процесс в электрической цепи — это электромагнитный процесс, возникающий в электрической цепи при переходе от одного установившегося (принужденного) режима к другому. Установившимся (принужденным) называется режим работы электрической цепи, при котором напряжение и токи цепи в течение длительного времени остаются неизменными.
Такой режим в электрической цепи устанавливается при длительном действии источников постоянной или переменной ЭДС при неизменных параметрах этой цепи R, L и С.
Переходный процесс вызывается коммутацией в цепи. Коммутацией называется процесс замыкания или размыкания рубильников или выключателей. Переходный процесс может быть вызван изменением параметров электрической цепи R, L или С.
Переходный процесс базируется на двух законах коммутации:
- ток в индуктивности не может изменяться скачком;
- напряжение на емкости не может изменяться скачком.
Действительно, если ток в индуктивности L изменяется скачком, т. е. мгновенно, то ЭДС самоиндукции eL становится бесконечно большой (при
В реальных цепях ЭДС самоиндукции может иметь только конечные значения.
Если в цепи с емкостью С напряжение на ее обкладках изменяется скачком, т. е. мгновенно, то появляется бесконечно большой зарядный (или разрядный) ток (при 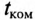
Ток в электрических цепях может иметь только конечные значения.
Переходный процесс является быстропротекающим процессом, длительность которого обычно составляет десятые, сотые и даже миллионные доли секунды и сравнительно редко — секунды и даже десятки секунд.
Таким образом, один установившийся режим цепи отделяется от другого некоторым промежутком времени, в течение которого происходит постепенный переход от прежнего состояния цепи к новому.
Переходный процесс в линейных цепях можно рассматривать как результат наложения двух процессов:
- нового установившегося режима, который наступает после коммутации;
- свободного процесса, обеспечивающего переход цепи от прежнего установившегося режима к новому установившемуся режиму.
Таким образом, ток i цепи в течение переходного процесса можно представить суммой двух токов: нового установившегося 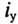
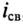
Аналогично напряжение в течение переходного процесса равно
В результате переходного процесса происходят изменения тока, напряжения, фазы, частоты и т.д.
Изучение переходных процессов очень важно, так как оно позволяет выявить возможные превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изоляции установки, позволяет выявить возможные броски токов, величина которых в десятки раз превышает установившийся. Изучение переходных процессов позволяет выявить ситуации, возникающие в электрических цепях при коротком замыкании, резком включении и выключении рубильников, и прочие режимы работы цепи.
Видео:Заряд разряд конденсатораСкачать

Переходный процесс в электрической цепи
Переходный процесс в электрической цепи — это процесс, возникающий в электрической цепи при различных воздействиях, приводящих их из стационарного состояния в новое стационарное состояние, когда при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.
Подключение катушки индуктивности к источнику с постоянным напряжением
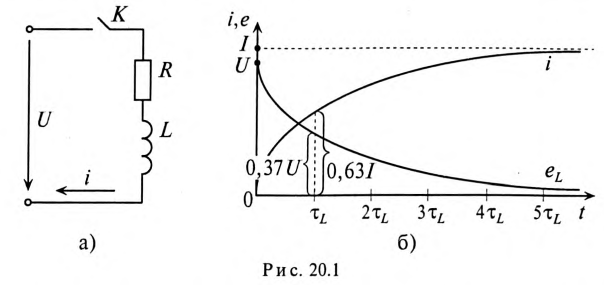
Если катушку индуктивности (RL) подключить к источнику с постоянным напряжением U (замыкание ключа К), то ток i в не-разветвленной цепи (рис. 20.1а) будет увеличиваться от нуля (в начале переходного процесса) до установившегося значения
Установившийся, т.е. постоянный, ток I не индуктирует в катушке ЭДС самоиндукции, поэтому индуктивное сопротивление в установившемся режиме при условии (20.3) отсутствует.
Этот увеличивающийся ток i индуктирует в индуктивности L катушки ЭДС самоиндукции (см. (9.11))
Следовательно, для любого момента времени переходного процесса по второму закону Кирхгофа можно записать
Разделив уравнение (20.4) на R, получают
В уравнении (20.5) 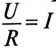
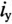
Отношение — 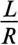
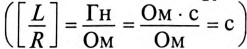
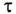
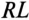
Тогда уравнение (20.5) можно записать в виде
Если это уравнение проинтегрировать, предварительно разделив переменные (ток и время), а затем спотенцировать, то получим выражение
где е — основание натурального логарифма (е=2,71); I — установившийся ток (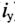
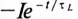
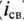
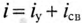
Таким образом, уравнение, которое позволяет определить вели-шу тока в цепи с индуктивностью L в любой момент переходно-процесса RL-цепи при подключении реальной катушки индук-1Вности к источнику с постоянным напряжением U, записывается в виде
Воспользовавшись Приложением 9, по выражению (20.10) можно определить, что за время t= 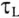
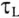
Теоретически переходный процесс происходит бесконечно долго. Практически переходный процесс в рассматриваемой цепи считается законченным, когда ток i увеличивается до 99 % установившегося тока I.
Как видим, чем больше xL, тем больше времени t длится перечный процесс.
Таким образом, постоянная времени xL определяет скорость греховного процесса или его длительность.
ЭДС самоиндукции в рассматриваемой цепи, вызванная свободным током 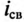
Таким образом, ЭДС самоиндукции в 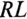
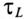
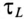
Увеличение тока и уменьшение ЭДС самоиндукции катушки при подключении катушки к источнику с постоянным напряжением U показаны на графике рис. 20.1б.
Отключение и замыкание RL-цепи
Если цепь с катушкой, в которой проходит установившийся ток I (рис. 20.1а), разомкнуть, то ток i в такой цепи с большой скоростью уменьшается до нуля и в катушке индуктируется большая ЭДС самоиндукции eL
Эта ЭДС полностью приложена к клеммам ключа, так как при размыкании сопротивление ключа становится бесконечно большим. Эта ЭДС вызывает значительное увеличение электрического поля между контактами ключа, а следовательно, и напряженности поля. Большая напряженность электрического поля может вызвать искровой и даже дуговой разряд между размыкающимися контактами ключа, в результате чего обгорают контакты ключа.
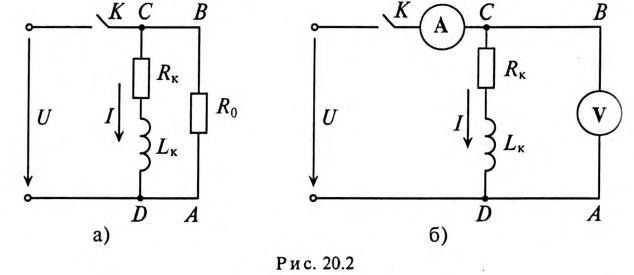
Поэтому рубильники в RL-цепях шунтируются специальными устройствами, которые обеспечивают гашение дугового разряда. Для гашения дугового разряда необходимо одновременно с отключением катушки индуктивности от источника замкнуть ее на разрядное сопротивление R0 (рис. 20.2а).
Уменьшение тока 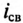
Наглядно это уменьшение можно наблюдать на рис. 20.1б, если кривую изменения eL считать кривой уменьшения тока 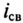
Постоянная времени при отключении катушки от источника с постоянным напряжением U определяется как и при включении катушки на это напряжение, т.е.
Если катушку с установившимся током I, зашунтированную сопротивлением Ro (рис. 20.2а), отключить от источника (разомкнуть ключ К), то в замкнутом контуре ABCD в начальный момент коммутации 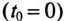
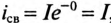
Для определения активного сопротивления катушки 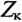
Как видно, за счет переходных процессов в цепях с индуктивностью возникают большие токи и напряжения. С этим необходимо считаться и учитывать при проектировании и эксплуатации цепей с индуктивностью.
Зарядка, разрядка и саморазрядка конденсатора
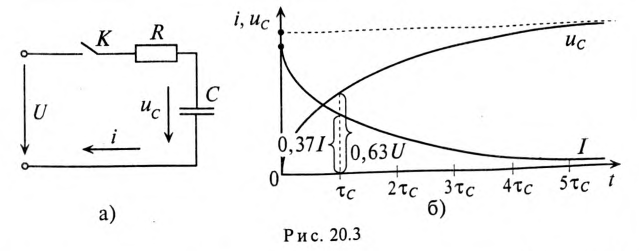
Если конденсатор с сопротивлением (утечки) R и емкостью С подключить к источнику с постоянным напряжением U (замыканием ключа К), то в цепи (рис. 20.3а) появится ток зарядки конденсатора (см. (11.16)):
где 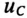
По второму закону Кирхгофа для цепи зарядки конденсатора (рис. 20.3а) можно записать уравнение
где произведение RC имеет размерность времени, обозначается буквой 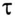
Уравнение (20.13) можно записать в виде
Если в уравнении (20.15) разделить переменные, проинтегрировать, а затем спотенцировать, то получится выражение
где U — установившееся напряжение 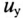
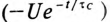
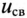
Следовательно, напряжение на заряжающемся конденсаторе в любой момент времени t переходного процесса определяется выражением
По (20.17), пользуясь Приложением 9, можно определить, что за время t= 
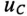

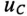
Теоретически зарядка конденсатора длится бесконечно долю а практически конденсатор считается заряженным, когда напряжение на нем достигает 99 % напряжения источника U.
Таким образом, и в RC-цепи, чем больше постоянная времени 

Ток i при зарядке конденсатора (см. (20.13)) уменьшается по за кону
(20. IS)
где 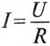
За время t= 

Графики изменения напряжения на конденсаторе и тока в цепи арядки конденсатора изображены на рис. 20.36.
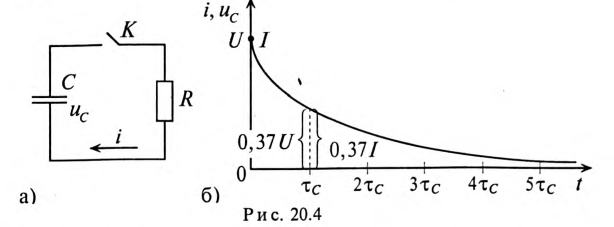
Если конденсатор емкостью С, заряженный предварительно до напряжения U, разряжать через резистор с сопротивлением R рис. 20.4а), то напряжение 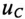
где U — напряжение на конденсаторе до начала разрядки (при t= 0), а 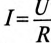

За время t= 
Если конденсатор емкостью С, заряженный до напряжения U, отсоединить от источника, то он будет разряжаться через свой диэлектрик. Напряжение на нем будет уменьшаться по закону 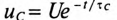
Постоянная времени саморазряда зависит от физических свойств диэлектрика
где р — удельное сопротивление диэлектрика; 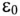
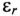
Для определения напряжения, тока, ЭДС в любой момент переходного процесса 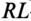
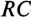
Пример 20.1
Катушка электромагнита с параметрами 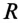
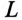
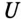
Решение
Установившийся ток
Постоянная времени для катушки
Подставляем значение величин в (20.10):
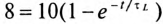
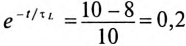
По Приложению 9 определяется 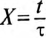
ЭДС самоиндукции за время 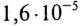
Пример 20.2
К зажимам катушки индуктивности с параметрами 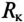
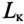
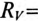
Определить напряжение на зажимах вольтметра и ток в обмотках прибора (обмотки соединены последовательно) при t=0, если размыкание рубильника К произойдет мгновенно и дуги не возникнет.
Решение
До размыкания рубильника через катушку проходил ток
В момент размыкания рубильника (t = 0) весь этот ток проходит обмоткам вольтметра. При этом на вольтметре напряжение cтанет равным
Такого напряжения (10 кВ) и такого тока (2 А) обмотка вольтметра (обычно подвижная обмотка электродинамического прибора рассчитана на ток порядка десятков, максимум, сотен миллиампер) не выдержит и сгорит.
При размыкании рубильника с конечной скоростью между расходящимися контактами рубильника К (рис. 20.26) возникнет электрическая дуга. Это приведет к тому, что увеличение напряжения на вольтметре и тока через обмотки вольтметра будет меньше, чем в рассмотренном выше случае (мгновенное размыкание рубильника). Однако меры предосторожности для сохранения вольтметра и рубильника, описанные выше, нужно соблюдать.
Пример 20.3
Конденсатор емкостью С= 2 мкФ через сопротивление R= 500 кОм подключается к источнику с постоянным напряжением U= 220 В.
Определить напряжение на конденсаторе 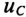
Решение
Постоянная времени заряда конденсатора
Напряжение на конденсаторе через 2 с от начала заряда
Ток в цепи заряда конденсатора через 2 с от начала заряда
так как
Время t’ заряда конденсатора до напряжения 150 В определяется по формуле (20.17):
Откуда
Из таблицы показательных функций (Приложение 9) находят t’= 1,14 с.
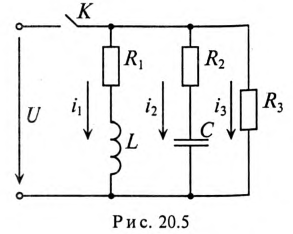
Пример 20.4
Параметры цепи, изображенной на рис. 20.5, следующие:
Определить значение токов в ветвях через время t= 2 с после замыкания ключа К.
Решение
Для ветви (1) с индуктивностью определяются:
установившийся ток
и постоянная времени
Тогда ток через 2 с будет равен
Для ветви (2) с емкостью определяются:
максимальный установившийся ток по окончании переходного процесса
и постоянная времени 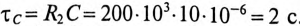
Тогда ток зарядки через 2 с будет равен
Для ветви (3) с активным сопротивлением 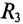
Постоянная времени 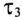
Через 2 с значение тока будет таким же, т. е.
Видео:Разрядка конденсатора .ТеорияСкачать

Переходные процессы в электрических цепях. Классический метод расчета
Возникновение переходных процессов:
В предыдущих главах рассматривались установившиеся процессы в линейных электрических цепях, т. е. такие процессы, при которых напряжения и токи либо неизменны во времени (цепи постоянного тока), либо представляют собой периодические функции времени (цепи переменного тока).
Наступлению установившегося процесса, отличного от первоначального режима работы цепи, предшествует, как правило, переходный процесс, при котором напряжения и токи изменяются непериодически.
Переход от одного режима работы цепи к другому может быть вызван изменением параметров или схемы цепи, называемым в общем случае в электротехнике коммутацией.
Можно теоретически считать, что коммутация цепи производится мгновенно, т. е. на включение, выключение или переключение цепи время не расходуется. Тем не менее переход от исходного режима работы цепи к последующему установившемуся процессу происходит не мгновенно, а в течение некоторого времени. Объясняется это тем, что каждому состоянию цепи соответствует определенный запас энергии электрических и магнитных полей. Переход к новому режиму связан с нарастанием или убыванием энергии этих полей. Энергия 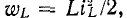
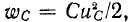
Если исключить случаи размыкания индуктивности и замыкания накоротко емкости и рассматривать цепи, в которых энергия, накапливаемая в магнитном или электрическом поле, может рассеиваться в виде теплоты в сопротивлениях, то, считая, что коммутация происходит мгновенно, можно искрообразование не учитывать.
Для завершения переходного и наступления установившегося процессов теоретически требуется бесконечно большое время. Практически, однако, время переходного процесса определяется малым интервалом, по истечении которого токи и напряжения настолько приближаются к установившимся значениям, что разница оказывается практически неощутимой. Чем интенсивнее происходит рассеяние энергии в сопротивлениях, тем быстрее протекает переходный процесс.
Если бы электрическая цепь состояла только из сопротивлений и не содержала индуктивностей и емкостей, то переход от одного установившегося состояния к другому совершался бы мгновенно, без затраты времени. В реальных электротехнических устройствах тепловые потери, обусловленные током, магнитные и электрические поля сопутствуют друг другу. Применяя специальные схемы и подбирая соответствующие параметры цепи, можно в зависимости от необходимости ускорить или замедлить переходный процесс.
В одних случаях переходные процессы в электрических цепях нежелательны и опасны (например, при коротких замыканиях в энергетических системах). В других случаях переходный процесс представляет собой естественный, нормальный режим работы цепи, как это, например, имеет место в радиопередающих и радиоприемных устройствах, системах автоматического регулирования и других цепях.
Существуют различные методы расчета переходных процессов в линейных электрических цепях. Настоящая глава посвящена классическому методу решения дифференциальных уравнений, описывающих переходные процессы.
Законы коммутации и начальные условия
Высказанные выше положения о том, что запас энергии магнитного или электрического поля может изменяться только плавно, без скачков, выражают принцип непрерывности во времени потокосцепления индуктивности и электрического заряда емкости и называются законами коммутации.
Невозможность скачкообразного изменения потокосцепления следует из того, что в противном случае на индуктивности появилось бы бесконечно большое напряжение 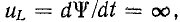
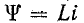
Аналогично невозможность скачкообразного изменения электрического заряда q следует из того, что в противном случае через емкость проходил бы бесконечно большой ток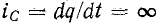
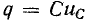
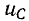
При этом следует отметить, что в цепях с идеализированными сосредоточенными параметрами скачкообразно могут изменяться: 1) токи в сопротивлениях и емкостях и 2) напряжения на сопротивлениях и индуктивностях.
Значения тока в индуктивности и напряжения на емкости в момент коммутации называются независимыми начальными условиями.
Обычно принимают, что коммутация происходит в момент времени t= 0; тогда ток в индуктивности и напряжение на емкости в момент времени непосредственно перед коммутацией обозначаются через 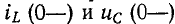
На основании законов коммутации: 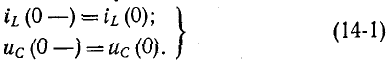
Эти равенства выражают начальные условия цепи, в которых происходит коммутация.
При нулевых начальных условиях, т. е. косца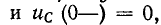
В случае ненулевых начальных условий, т. е. когда 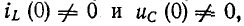
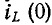
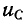
Независимые начальные условия характеризуют энергию магнитного и электрического полей, запасенную к моменту коммутации, и для расчета переходного процесса обязательно требуется знание этих начальных условий, причем совершенно безразлично, каким образом эти условия в цепи были созданы.
При расчете переходных процессов в разветвленных электрических цепях наряду с независимыми начальными условиями используются так называемые зависимые начальные условия, а именно: значения токов, напряжений и их производных в начальный момент времени (t = 0).
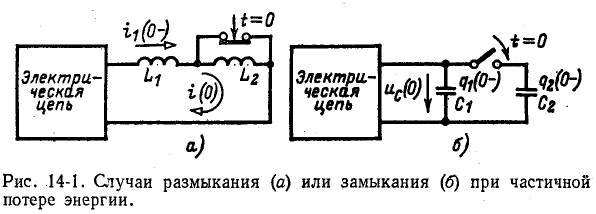
До сих пор нами исключались из рассмотрения случаи коммутации, при которых неизбежно между контактами возникает искра или дуга. Один из таких случаев показан на рис. 14-1, а. До коммутации ток проходит через индуктивность 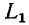
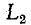
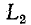
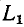
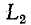
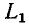
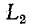
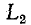
замкнуться и через межвитковую емкость. После быстрого погасания дуги токи в 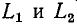
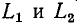
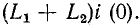
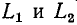
Найденный таким образом ток 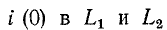
При коммутациях в цепях с емкостями при отсутствии сопротивлений также возможны весьма быстрые перераспределения зарядов, условно рассматриваемые как мгновенные. В этом случае применим принцип непрерывности суммарного заряда. Полученные при этом значения зарядов и напряжений на отдельных емкостях используются в расчете последующего переходного процесса как независимые начальные условия.
Например, в случае схемы на рис. 14-1, б принцип непрерывности суммарного заряда до и после коммутации выражается равенством
При сделанном допущении в остальной электрической цепи, соединенной с емкостями, не возникает бесконечно большого тока, так как суммарный заряд не изменяется скачкообразно при t=0.
В процессе рассматриваемой коммутации энергия электрического поля уменьшится, так как часть ее превратится в тепло в очень малом сопротивлении проводника при очень большом токе, а также сможет выделиться в искре и излучиться.
Установившийся и свободный режимы
В общем случае анализ переходного процесса в линейной цепи с сосредоточенными параметрами r, L, С и М сводится к решению обыкновенных линейных неоднородных дифференциальных уравнений, выражаюших законы Кирхгофа. Эти уравнения представляют собой линейную комбинацию напряжений, токов, их первых производных и интегралов по времени.
Например, если какая-нибудь э. д. с. е (t) включается в цепь, состоящую из последовательно соединенных r, L и С, то интегродифференциальное уравнение имеет вид:
Это уравнение после дифференцирования приводится к неоднородному дифференциальному уравнению второго
Как известно, общий интеграл такого^ уравнения равен сумме частного решения неоднородного уравнения и общего решения однородного уравнения.
Частное решение выражает установившийся режим, задаваемый источником.
Расчеты установившихся токов рассмотрены в предыдущих главах.
Общее решение физически определяет поведение цепи при отсутствии внешних источников электрической энергии и заданных начальных условиях. Функции, определяемые общим решением, называются свободными составляющими (токов, напряжений и пр.).
В случае, рассмотренном выше, однородное уравнение имеет вид:
и соответствующее ему характеристическое уравнение
Если корни характеристического уравнения обозначить через 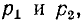
где 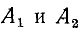
Полный переходный ток в цепи равен сумме установившегося и свободного токов:
Аналогично напряжение, заряд, магнитный поток и другие функции на любом участке цепи в переходном режиме состоят из установившейся и свободной составляющих.
На основании законов коммутации можно найти начальные независимые условия 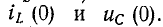
откуда
Итак, начальные значения свободных функций 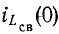
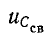
В частном случае при нулевых начальных условиях:
В зависимости от порядка дифференциальных уравнений, описывающих исследуемые переходные процессы, различают цепи первого, второго и более высокого порядков.
В цепях первого порядка накопление энергии происходит только в одном элементе, L или С в форме магнитной энергии, или электрической энергии . Одноконтурная цепь, содержащая элементы, в которых накапливается энергия обоих видов — магнитная « электрическая, представляет собой цепь второго порядка . Разветвленные цепи могут быть более высокого порядка.
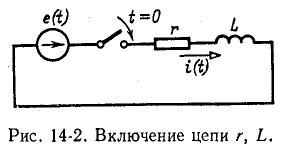
Переходный процесс в цепи r, L
Положим, что в момент t = 0 цепь, состоящая из сопротивления r и индуктивности L, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-2).
Дифференциальное уравнение для времени 
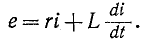
Характеристическое уравнение имеет вид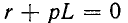
Отсюда свободный ток
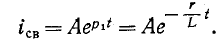
Переходный ток в цепи определится суммой установившегося и свободного токов:
Установившийся ток может быть найден, если задана э. д. с. е (t).
Рассмотрим три случая:
1) включение в цепь г, L постоянной э. д. с. £;
2) короткое замыкание цепи г, L
3) включение в цепь г, L синусоидальной э. д. с.
1. Включение в цепь г, L постоянной э. д. с.
При включении в цепь г, L постоянной э. д. с. Е установившийся ток равен Е’/г. Поэтому согласно (14-9)
Постоянная интегрирования А находится по начальному условию
Согласно уравнению (14-10) при t — 0
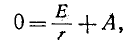
откуда 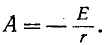
здесь 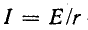
В начальный момент t = 0 э. д. с. самоиндукции 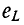
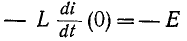
С течением времени э. д. с. самоиндукции убывает, а ток в цепи возрастает, асимптотически приближаясь к установившемуся значению.
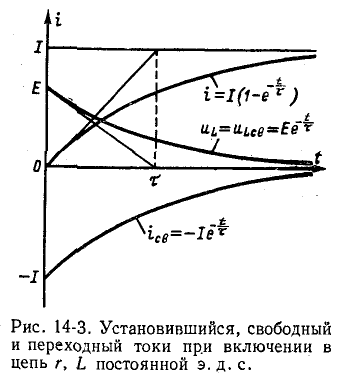
На рис. 14-3 показаны кривые установившегося, свободного и переходного токов; на том же рисунке изображена кривая напряжения на индуктивности 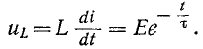
Из курса математического анализа известно, что если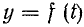
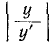
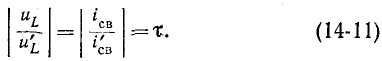
Величина 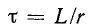
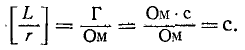
Выражение (14-11) показывает, что постоянная времени графически определяется длиной подкасательной к кривой 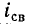
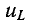
Нарастание тока происходит тем быстрее, чем меньше постоянная времени и соответственно чем быстрее убывает э. д. с. самоиндукции. Для различных моментов времени ток в цепи, выраженный в процентах конечного (установившегося) значения составляет:
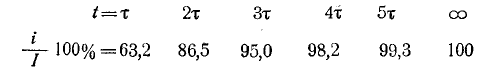
Следовательно, постоянная времени цепи г, L равна промежутку времени, в течение которого свободная составляющая тока убывает в е = 2,718 раза и соответственно ток в этой цепи, включенной на постоянное напряжение, достигает 63,2% своего установившегося значения.
Как видно из рис. 14-3 и приведенной выше таблицы», переходный процесс теоретически длится бесконечно долго. Практически же можно считать, что он заканчивается спустя
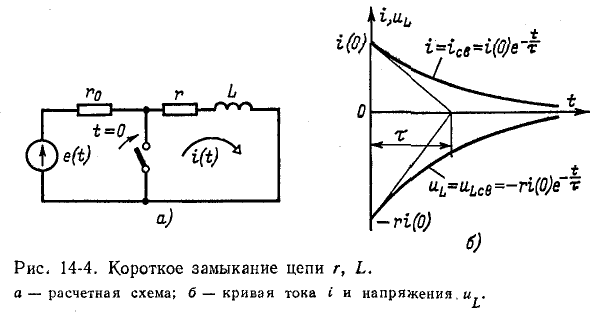
2. Короткое замыкание цепи r, L.
Положим, что цепь r, L, присоединенная к источнику постоянного или переменного напряжения, замыкается при t = 0 накоротко (рис. 14-4, а). В образовавшемся при этом контуре r, L благодаря наличию магнитного поля индуктивной катушки ток исчезает не мгновенно: э. д. с. самоиндукции, обусловленная убыванием магнитного потока, стремится поддержать ток в контуре за счет энергии исчезающего магнитного поля.
По мере того как энергия магнитного поля постепенно рассеивается, превращаясь в сопротивлении г в тепло, ток в контуре приближается к нулю.
Процесс, происходящий в короткозамкнутом контуре г, L, является свободным; установившийся ток в данном случае равен нулю.
Положив в (14-9) 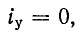
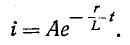
Постоянная интегрирования А находится из начального условия
здесь i (0—) — значение тока в индуктивности в момент, непосредственно предшествовавший короткому замыканию; оно может быть положительным или отрицательным.
На рис. 14-4, б изображены кривые спада тока в короткозамкнутом контуре и кривая напряжения на индуктивности

Постоянная времени контура 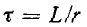
Переходный процесс в короткозамкнутом контуре заканчивается теоретически при 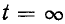
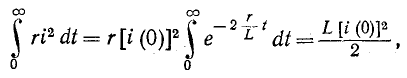
т. е. вся энергия, запасенная в магнитном поле катушки до коммутации.
Так же как и в предыдущем случае, переходный процесс в короткозамкнутом контуре можно практически считать законченным спустя
3. Включение в цепь r, L синусоидальной э. д. с.
При включении в цепь r, L синусоидальной э. д. с. 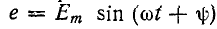
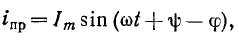
где 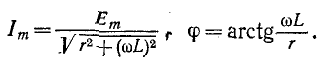
На основании (14-9) 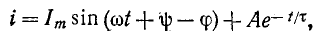
где 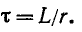
Постоянная интегрирования определяется по начальному условию
Следовательно, 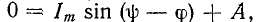
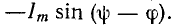
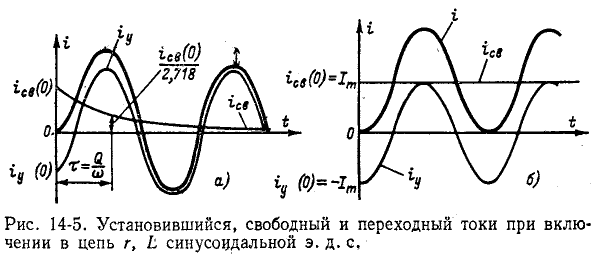
На рис. 14-5, а изображены кривые 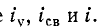
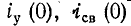
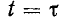
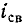
контура Q и обратно пропорциональна частоте 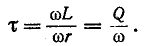
Если в момент коммутации (t = 0) ток 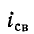
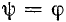
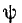
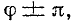
Если же коммутация происходит при 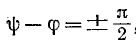
а именно 
гает экстремального значения (положительного или отрицательного) в конце первого полупёриода. Однако даже в предельном случае, когда r= 0 и, следовательно, 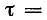
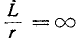
При достаточно большой постоянной времени 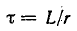
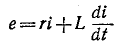
можно пренебречь по сравнению со вторым слагаемым, приняв приближенно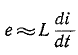
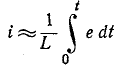
Следовательно, цепь с последовательно соединенными сопротивлением и индуктивностью при большой постоянной времени можно рассматривать как интегрирующее звено.
В свою очередь при достаточно малой постоянной времени, пренебрегая вторым слагаемым уравнения, приближенно получаем:
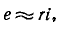
откуда
.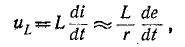
т. e. цепь с последовательно соединенными сопротивлением и индуктивностью при малой постоянной времени представляет собой дифференцирующее звено.
В обоих случаях функция е(t) может быть произвольной.
Интегрирующие и дифференцирующие звенья входят в качестве элементов в системы автоматического управления и регулирования.
Переходный процесс в цепи r, С
Положим, что в момент t = О цепь, состоящая из сопротивления г и емкости С, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-6).
На основании второго закона Кирхгофа уравнение для времени t 
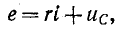
где 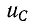
С учетом того, что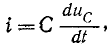
получим:
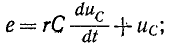
здесь искомой величиной является напряжение на емкости.
Характеристическое уравнение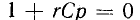
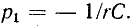
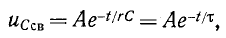
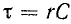
Переходное напряжение на емкости равно сумме принужденного и свободного напряжений:
В свою очередь ток в контуре
Рассмотрим три случая:
1) включение в цепь г, С постоянной э. д. с.
2) короткое замыкание цепи r, С
3) включение в цепь r, С синусоидальной э. д. с.
Включение в цепь r, С постоянной э. д. с.
Включим постоянную э. д. с. Е в цепь с сопротивлением г и предварительно заряженной емкостью С (полярности заряженной емкости указаны на рис. 14-6 знаками + и —); начальное напряжение на емкости
(0) обозначим для простоты через U.
Установившееся напряжение на емкости равно э. д. с. источника. Поэтому согласно (14-12)
Постоянная интегрирования А, входящая в (14-14), находится по начальному условию:
При t = 0 имеем 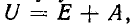
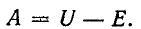
Согласно (14-13) ток в контуре
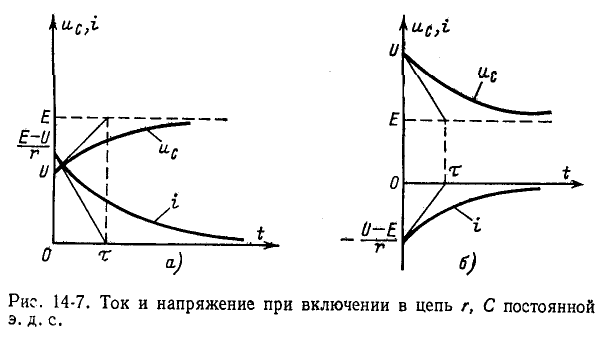
Если Е > U, то с течением времени напряжение на емкости возрастает, стремясь к установившемуся значению Е, а ток убывает, стремясь в пределе к нулю; на рис. 14-7, а изображены кривые нарастания 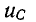
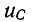
Если Е 0), убывающей (с 0) или убывающей (с 1 В случае, когда э. д. с. изменяется в виде импульса, имеющего кусочно-аналитическую форму, представляется часто целесообразным применять интеграл Дюамеля
токи же 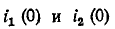
Подстановка в эти уравнения найденных значений 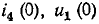
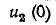
Начальное значение производной тока в индуктивности определяется также из уравнения Кирхгофа:
откуда при t = О
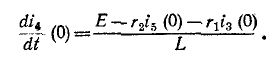
Пример (4-2. Определить ток i в иепи на рис. 14-17, если известно, что е = E = 100 В,
Подстановка заданных значений в приведенное выше характеристическое уравнение дает:
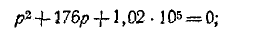
корни характеристического уравнения комплексные:
В начальный момент 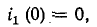
Производная тока по времени
В начальный момент
Следовательно, в начальный момент напряжение на ветви 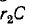
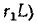
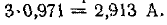
производной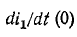
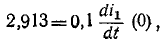
Следовательно, подставляя значение 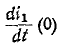
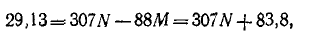
откуда
Итак,
Переходные процессы в цепях с распределенными параметрами
Переходные процессы в цепях с распределенными параметрами (в линиях, обмотках электрических машин и т. п.) возникают при коммутациях, передаче непериодических сигналов или под влиянием внешнего электромагнитного поля (например, при грозовых разрядах). Для исследования переходных процессов в однородных цепях с распределенными параметрами пользуются дифференциальными уравнениями (11-2) в частных производных: 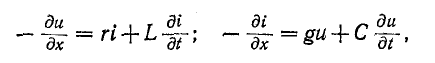
где r, L, g и С — параметры цепи на единицу длины; х — координата рассматриваемой точки, отсчитываемая от начала цепи.
В общем виде решение этих дифференциальных уравнений достаточно сложно. Решение упрощается, если пренебречь потерями В этом случае
е. считать, что r и g равны нулю.
Дифференцируя (14-28) по х:
и используя (14-29), получаем: 
Дифференциальное уравнение (14-30) известно в математической физике под названием уравнения ко—лебаний струны. Его решение дано Даламбером и имеет вид: 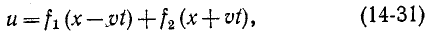
где 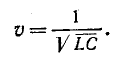
Первая слагающая представляет собой одиночную прямую волну напряжения, которая без изменения перемещается в сторону возрастающих х, т. е. от начала к концу цепи. Для всех значений х, при которых 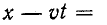
Вторая слагающая представляет собой одиночную о б -ратную волну напряжения, которая без изменения перемещается в противоположном направлении.
Для нахождения тока произведем замену переменных, обозначив 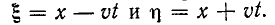
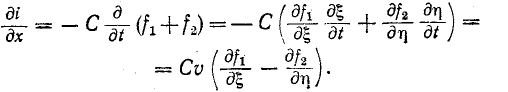
Но
Интегрирование последнего уравнения дает 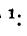
Выражения (14-31) и (14-32) записываются сокращенно:
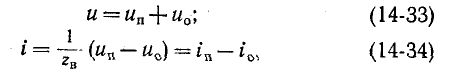
здесь 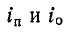
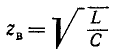
Следовательно, напряжение и ток прямой и соответственно обратной волн связаны законом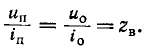
Аналогичный результат был получен для установившихся прямой и обратной волн при рассмотрении синусоидального режима в однородной линии. Физически установившиеся волны представляют собой бесконечные суммы прямых и обратных одиночных волн, отраженных от обоих концов линии.
Итак, при отсутствии потерь в однородной цепи с распределенными параметрами напряжение и ток могут быть представлены как сумма и разность двух волн, движущихся с одинаковой скоростью 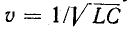
Если на пути распространения волны встречается неоднородность, например воздушная линия переходит в кабельную или волна достигает конца линии (разомкнутого или замкнутого через сопротивление или на короткое), происходит отражение волны. В зависимости от характера неоднородности отражение может быть частичным или полным. В первом случае наряду с отраженной волной возникает преломленная волна, распространяющаяся за место нарушения однородности; во втором случае преломленная волна отсутствует.
Обозначим 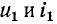
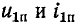
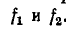
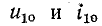
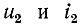
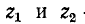
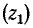
В месте неоднородности выполняется условие равенства
напряжений и токов: 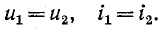
Следовательно, 
Подстановка в (14-36) значений 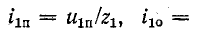
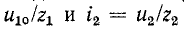
В результате совместного решения уравнений (14-35) — (14-37) находятся отраженная 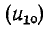
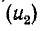
где 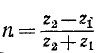
Соответственно ток отраженной волны
а ток преломленной волны
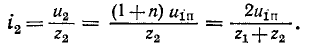
Последнее выражение показывает, что ток в конце линии после отражения можно найти как ток в эквивалентной цепи, в которую включается напряжение, равное двойному напряжению падающей волны, и которая состоит из волнового сопротивления первой линии 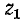
Опишем процесс включения однородной линии без потерь. После присоединения линии к источнику э. д. с. по линии начнет распространяться зарядная волна, создающая напряжение и ток. Если в конце линии присоединена нагрузка, равная волновому сопротивлению линии,
то падающая волна, достигнув ее, не отразится и в линии сразу наступит установившийся режим. Если же нагрузка с линией не согласована, то падающая зарядная волна, достигнув конца линии, претерпит отражение. Распространяясь в обратную сторону, отраженная волна сложится с падающей, причем напряжения волн суммируются, а токи вычитаются (алгебраически). Достигнув начала линии, обратная волна снова отразится от источника э. д. с., как от короткозамкнутого конца; появится новая прямая волна напряжения и тока, которая также отразится от конца, и т. д. Процесс будет продолжаться до наступления установившегося режима. Теоретически в идеальной линии без потерь при чисто реактивной нагрузке процесс колебаний будет продолжаться бесконечно долго. В реальной линии при наличии потерь волны напряжения и тока будут постепенно затухать в направлении распространения.
Напряжение и ток в линии в произвольный момент времени определятся как алгебраические суммы и соответственно разности напряжений и токов прямых и обратных волн.
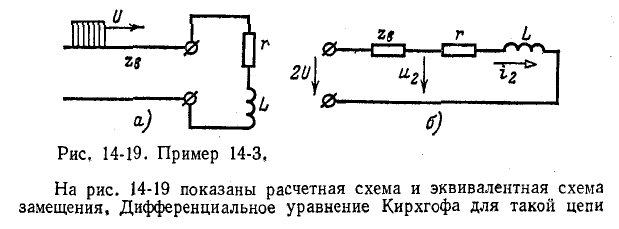
Пользуясь формулами и схемой замещения, описанной выше, можно найти напряжение и ток, возникающие в месте присоединения сосредоточенной нагрузки или перехода одной линии в другую (см. пример 14-3).
Следует отметить что индуктивность, включенная последовательно в линию, или емкость, включенная параллельно проводам линии, сглаживает фронт преломленных волн; активное сопротивление, включенное в линию параллельно, уменьшает преломленную волну.
Пример 14-3. К концу линии, имеющей волновое сопротивление 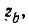
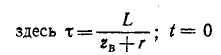
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Переходные процессы в линейных цепях
- Переходные процессы в нелинейных цепях
- Переходные процессы в электрических цепях с сосредоточенными параметрами
- Переходные процессы в колебательных контурах
- Цепи с взаимной индукцией
- Трехфазные цепи
- Периодические несинусоидальные напряжения и токи в линейных цепях
- Нелинейные цепи переменного тока
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
💡 Видео
Зарядка конденсатораСкачать

Разрядка конденсатораСкачать

ПОЧИНИЛИНАХ 3!!! Разряд конденсатора 400V. Как правильно разрядить чтобы не еб..уло))Скачать

разряд высоковольтного конденсатораСкачать

разряд конденсатораСкачать

2020 г. Дифференциальные уравнения для электрических цепей. Лекция и практикаСкачать

Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Урок 8. Перезарядка конденсатора. Плотность тока смещения. Ток смещения. Физика 11 классСкачать

Разрядник конденсаторов с указателем напряжения.Скачать

ОПАСНОСТЬ ОТ КОНДЕНСАТОРОВСкачать

Урок 17. Как работает Интегрирующая и Дифференцирующая RC-цепь | Самое понятное объяснениеСкачать

Как правильно разрядить конденсаторСкачать

Как безопасно разрядить электролитический конденсатор! Делаем разрядник.Скачать