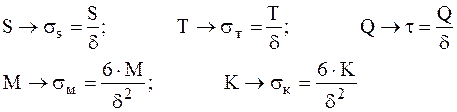Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Осесимметричные оболочки вращения. Их основные нагрузки и напряжения. Уравнения Лапласа.
Оболочка вращения называется осесимметричнойесли она нагружена: силами распределенными симметрично вокруг оси; краевыми силами, распределенными равномерно по параллельному кругу; краевыми моментами, равномерно распределенными по параллельному кругу.
Самым общим случаем нагружения каждой точки поперечного сечения осесимметричных оболочек вращения действуют следующие удельные нагрузки, распределенные равномерно по толщине стенки оболочки:
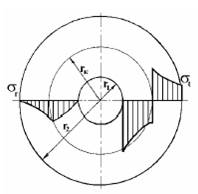
1. S – меридиональная сила – это сила приходящаяся на единицу длины параллельного круга и растягивающая элемент в меридиональном направлении.
2.Т – кольцевая сила – это сила приходящаяся на единицу длины меридиана и стремящаяся растянуть элемент в направлении параллельного круга.
3.М – меридиональный момент – это момент, приходящийся на единицу длины параллельного круга и стремящийся изменить кривизну элемента в направлении меридиана.
4.К – кольцевой момент – изгибающий момент, приходящийся на единицу длины меридиана и стремящийся изменить кривизну элемента в направлении параллельном меридиана.
5.Q – поперечная сила – это сила, приходящаяся на единицу длины меридиана.
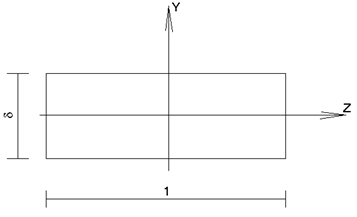
Напряжения, возникающие от действия удельных нагрузок определяются если предположить, что грани элемента к которому приложена нагрузка имеют форму прямоугольника с основанием равным 1 и высотой равной толщине стенки аппарата.
Согласно принципа суперпозиции (независимости действия сил) одноименные силы суммируются
Вывод: таким образом самым общим случаем нагружения ассиметричные оболочки вращения испытывают действия трех напряжений: меридиональное, кольцевое и касательное, которые учитывают действие всех внутренних удельных нагрузок.
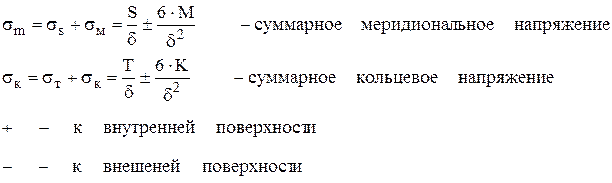
Теория расчета оболочек, которая учитывает действие всех внутренних удельных нагрузок – моментная теория расчета.
На практике при расчете тонкостенных оболочек вращения, находящихся под действием равномерно распределенного давления поперечную силу и изгибающие моменты не учитывают. Такую теорию расчета называют безмоментной теорией расчета оболочек.
Основным уравнением безмоментной теории расчета на прочность ассиметричных оболочек вращения нагруженных давлением является уравнение Лапласа.
,
Р – внутреннее давление;
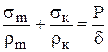
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать
Моментная теория осесимметричных цилиндрических оболочек
Цилиндрические оболочки (тонкостенные цилиндры) представляют собой наиболее распространенный частный вид оболочек вращения. Поскольку теория расчета цилиндрических оболочек значительно проще и нагляднее, чем теории расчета оболочек другой формы, традиционно эту теорию рассматривают отдельно от общего случая оболочек вращения.
Осесимметричная изгибная деформация оболочки возникает в местах приложения внешних кольцевых нагрузок, а также в местах закрепления или сопряжения цилиндрической оболочки с другими конструктивными элементами: днищами, кольцевыми ребрами и т.д.
Теория осесимметричной деформации цилиндрических оболочек основана на гипотезах Кирхгофа — Лява. Данные гипотезы рассматривались выше в параграфе, посвященном расчету пластин. Остановимся на этих гипотезах еще раз применительно к цилиндрическим оболочкам.
Гипотеза неизменности нормалей. Точки, лежащие на нормали к срединной поверхности оболочки до деформации, после деформации остаются лежать на одной прямой, перпендикулярной к деформированной срединной поверхности оболочки, при этом расстояние между точками не изменяется. Гипотеза носит геометрический характер и позволяет установить связь между деформированным состоянием в произвольной точке оболочки и изменением геометрии ее срединной поверхности. С ее помощью исследование деформации оболочки сводится к исследованию деформации ее срединной поверхности.
Гипотеза о ненадавливании слоев оболочки. Нормальные напряжения в площадках, параллельных срединной поверхности оболочки, считают пренебрежимо малыми, и напряженное состояние в материальных точках, принадлежащих оболочке, можно считать плоским напряженным состоянием.
Следует отметить, что между гипотезами изначально существует известное противоречие, поскольку соотношения закона Гука не допускают, чтобы напряжения и деформации, действующие в направлении нормали к срединной поверхности, одновременно равнялись нулю при ненулевых компонентах напряжений и деформаций в остальных направлениях. Тем не менее существующий расчетный опыт и его экспериментальная проверка показали, что указанные гипотезы приближенно выполняются с удовлетворительной для расчетных целей точностью, если толщина оболочки мала по сравнению с радиусом цилиндра.
При построении разрешающих соотношений теории предполагается справедливость основных допущений о материале оболочки, который считается однородным, изотропным и линейно-упругим, т.е. подчиняющимся закону Гука.
Введем обозначения: г — средний радиус цилиндра; h — толщина стенки цилиндра; х — координата, совпадающая со срединной поверхностью оболочки и отсчитываемая от торца в направлении оси цилиндра; и, w — перемещения произвольной точки срединной поверхности в осевом и в радиальном направлениях; у — расстояние от срединной поверхности до текущего слоя оболочки (
h/2 и Рх постоянны, или их изменение вдоль оси .г подчиняется линейному или квадратичному закону. Ограничиваясь только этими случаями и учитывая, что при указанных условиях производные выше второй степени но координатехотр„,рхи Тх равны нулю, получим для ш* следующее выражение:
Для практических целей общее решение уравнения (14.25), представленное в виде (14.32), недостаточно удобно, поэтому его преобразуют к другому виду, причем для длинных и коротких оболочек это преобразование делается по-разному.
Остановимся на вопросе определения констант интегрирования. Для этой цели необходимо использовать граничные условия на краях оболочки. На каждом краю обычно бывают заданы два условия (рис. 14.10).
Рис. 14.10. Варианты граничных условий
Если край жестко заделан (рис. 14.10, а), то значения функции прогиба и угла поворота на краю должны быть равными нулю:
Для шарнирно опертого края (рис. 14.10, б)
Для свободного края (рис. 14.10, в) 
При нагружении края оболочки заданной силой Qo и моментом М0 (рис. 14.10, г)
В случае сопряжения цилиндрической оболочки с оболочкой другого типа или плоским днищем используются условия равенства радиальных перемещений w (или равенство окружных деформаций г,); равенства углов поворота нормали 0; равенства изгибающих моментов Мт и равенства радиальных составляющих внутренних сил Q (сил распора).
Определение четырех постоянных интегрирования требует решения системы четырех уравнений с четырьмя неизвестными. Однако практически всегда оказывается возможным построить решение так, что две постоянные определяются сразу, а остальные — в результате решения системы двух уравнений с двумя неизвестными.
Видео:Симметричные системы #1Скачать
Тонкостенная осесимметричная оболочка
Тонкостенной осесимметричной называется оболочка, имеющая форму тела вращения толщина, которой мала по сравнению с радиусами кривизны ее поверхности (рис.1).
При расчете тонкостенных оболочек все нагрузки, действующие на них, прикладывают к срединной поверхности оболочки.
К тонким оболочкам могут быть отнесены такие часто встречающиеся элементы конструкций как резервуары, цистерны, газовые баллоны, корпуса аппаратов химических агрегатов и др.
При расчете таких элементов конструкций используется безмоментная теория оболочек, основные положения которой заключаются в следующем:
1. нагрузки, действующие на поверхности оболочки, могут считаться перпендикулярными им и симметричными относительно оси вращения оболочки;
2. вследствие малой толщины оболочки сопротивление изгибу отсутствует (изгибающий момент не возникает);
3. напряжения по толщине стенки оболочки распределены равномерно.
Из оболочки, изображенной на рис.1 выделим двумя меридиональными плоскостями nn1n2 и nn3n2, (т.е. плоскостями проходящими через ось симметрии оболочки), с углом dφ между ними и двумя плоскостями, перпендикулярными оси симметрии оболочки BC и AD, элементABCD.
Радиусы кривизны O2A и O2B элемента ABCD в меридиональной плоскости обозначим через R2, а радиусы кривизны O1B и O1C в плоскости, перпендикулярной меридиану, обозначим через R1. Нормальные напряжения, действующие по боковым граням AB и CD, соприкасающимся с меридиональными плоскостями, называются окружными напряжениями σt. Нормальные напряжения, действующие по боковым граням BС и AD, называются меридиональными напряжениями σs. Кроме напряжений σs и σt. на элемент оболочки действует нагрузка в виде давления q, перпендикулярного поверхности ABCD.
Рис.1
Основным уравнением безмоментной теории оболочек является уравнение Лапласа, которое имеет следующий вид
где δ — толщина оболочки.
Прежде чем перейдем к рассмотрению различных вариантов определения напряжений в оболочках остановимся на некоторых различиях, вызванных наличием газа или жидкости внутри оболочки.
В случае газового давления величина давления q постоянная во всех точках поверхности оболочки. Для резервуаров, наполненных жидкостью, значение q по их высоте переменно.
Для случая наполнения резервуара жидкостью необходимо учитывать, что если на какую-либо поверхность действует давление жидкости, то вертикальные составляющие сил давления равны весу жидкости в объеме, расположенном над поверхностью. Поэтому давление жидкости в различных сечениях оболочки будет различным, в отличие от давления газа.
Определим напряжения в сферических и цилиндрических оболочках т.к. они наиболее часто используются в промышленности.
Сферическая оболочка
Отсечем часть сферической оболочки нормальным коническим сечением с углом 2φ при вершине и рассмотрим равновесие этой части оболочки вместе с заключенной в ней жидкостью с удельным весом γ. Сферическую часть отделим от основной оболочки плоскостью, перпендикулярной оси симметрии.
Рис.2
На рис.2 изображена расчетная схема сферической оболочки радиусом Rs. Высота отсеченной поверхности 
. Давление q на отсеченную часть в этом и последующих случаях равно весу жидкости в объеме, расположенном над поверхностью, который равен
где 
— высота столба жидкости выше отсеченной части оболочки.
Уравнение равновесия отсеченной части может быть записано, как сумма проекций всех сил на вертикальную ось
В данном уравнении величина G – вес жидкости, заполняющей отсеченную часть сферической оболочки (см. рис.8.2).
где 
— объем нижней отсеченной части сферической оболочки.
Путем интегрирования объем сферического сегмента может быть определен по формуле
После подстановки уравнения (8.5) в выражение (8.4), и затем, в (8.3), получим конечное уравнение равновесия для сферической части сегмента
Из этого уравнения можно определить величину меридионального напряжения 
, и, после подстановки в уравнение Лапласа (16.1), найти величину окружного напряжения 
.
Цилиндрическая оболочка
Рассмотрим цилиндрическую оболочку радиусом 
, заполненную жидкостью с удельным весом γ (см. рис.3).
Рис.3
В данном случае цилиндрическая часть отделена от остальной части оболочки сечением, перпендикулярным оси симметрии.
Уравнение равновесия отсеченной части может быть получено, как сумма проекций всех сил на вертикальную ось.
где 
— вес жидкости, заполняющий отсеченную часть цилиндрической оболочки.
Объем цилиндра с высотой x и радиусом может быть определен по формуле
С учетом этого уравнение равновесия принимает вид
В этом уравнении, также как и в предыдущем случае, одна неизвестная
Для случая цилиндрической оболочки при подстановке в уравнение Лапласа необходимо учесть, что величина 
, значит
.
Коническая оболочка
Отсечем часть конической оболочки нормальным коническим сечением с углом 2φ при вершине и рассмотрим равновесие отсеченной части.
Рис.4
Как видно из рис.4 φ = π/2 — α.
Уравнение равновесия отсеченной части оболочки будет иметь вид
где — вес жидкости, заполняющий отсеченную часть конуса.
С учетом (8.11), выражение (8.10) имеет следующий вид
Из этого уравнения можно рассчитать величину меридионального напряжения и, подставив его в уравнение Лапласа, найти величину .
Возможно отделение сечением не нижней, а верхней части оболочки с последующей записью уравнения равновесия. Это делается для того, чтобы при составлении условий равновесия отсеченного элемента крепление оболочки не попадало в схему отсеченной части. В подобных вариантах во всех рассмотренных случаях изменится знак силы G, т.к. в этом случае ее направление будет совпадать с направлением вертикальной составляющей напряжения .
В этом случае, при расчете величины G, в качестве объема будет браться объем отсеченной верхней части 
, а при расчете величины q в формулу (8.2) во всех случаях войдет величина 
— высота столба жидкости в отсеченной нижней части оболочки. В остальном порядок расчета останется неизменным.
В случае, если жидкость находится в сосуде под давлением P, то при расчете величины q добавляется величина давления P. Формула (8.2) будет иметь следующий вид
В некоторых задачах отсеченная часть представляет собой не какой-то один элемент, а два или более состыкованных элемента. При этом вид уравнений равновесия остается неизменным, а изменяется только величина объема верхней или нижней части сосуда, однако, если известны зависимости, определяющие объемы элементов, то найти суммарный объем не представляет затруднения.
На рис.5, а показана схема оболочки вращения, состоящей из сферической, цилиндрической и конической оболочек. Крепление оболочки располагается на уровне стыка сферической и цилиндрической оболочек. Сосуд наполнен жидкостью, находящейся под давлением Р.
На рис.5, б показан пример построения эпюр напряжения. В левой половине оболочки расположена эпюра , а в правой .
Рис.5
Полученные построения справедливы для участков, находящихся на некотором удалении от линии закрепления оболочки и точек сопряжения сфера-цилиндр и цилиндр-конус. В точках сопряжения возникают эффекты, которые не могут быть учтены теорией безмоментногонапряженного состояния. Все это также относится и к точкам, непосредственно примыкающим к вершине конуса.
Толстостенный цилиндр
Толстостенным называется такой цилиндр, для которого отношение толщины стенки к внутреннему диаметру не менее 1/20.
Задача о расчете толстостенного цилиндра решается с учетом равномерно распределенного наружного давления 
и внутреннего давления 
. Мы исходим из того, что такая нагрузка не может вызвать деформации изгиба цилиндра.
Нормальные напряжения . в сечениях плоскостями, перпендикулярными оси симметрии О цилиндра нельзя считать равномерно распределенными по толщине стенки, как это делается при расчете тонкостенных оболочек вращения (рис.6).
Нормальные напряжения 
действующие по цилиндрической поверхности с радиусом r могут быть одного и того же порядка и даже превышать напряжение , что при тонкостенных цилиндрах невозможно.
Рис.6
В поперечных сечениях цилиндра касательные напряжения также предполагаются равными нулю, однако, возможно существование нормальных осевых напряжений 
, которые возникают как следствие нагружения цилиндра силами, действующими вдоль оси. В дальнейшем мы будем рассматривать открытые цилиндры, т.е. не имеющие днищ. Напряжения в таких цилиндрах равны нулю. Вывод формул расчета напряжений в толстостенных цилиндрах основан на том, что для них соблюдается гипотеза плоских сечений, т.е. поперечные сечения цилиндра, плоские до нагружения, останутся плоскими и после нагружения.
Основными уравнениями для расчета напряжений в толстостенных цилиндрах являются формулы Ламе:
При действии на цилиндр только наружного или внутреннего давления знаки эпюр , во всех точках цилиндра одинаковы. Эпюры изменения радиального и окружного напряжения для случая действия только наружного давления показаны на рис.7. Эти напряжения во всех точках цилиндра отрицательны, что соответствует сжатию.
Рис.7 Рис.8
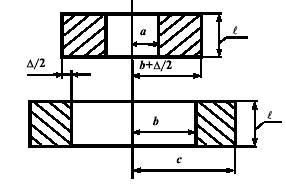
При нагружении внутренним давлением эпюры изменения радиального окружного напряжения показаны на рис.8. Окружное напряжение является расширяющим, а радиальное сжимающим.
Анализ формул Ламе показывает, что увеличение толщины не может во всех случаях обеспечить необходимой прочности цилиндра. Поэтому для сосудов высокого давления необходимо искать какие-то другие конструктивные решения. Одним из таких решений является создание составных, соединенных с натягом, цилиндров. Этот прием используется как в технике высоких давлений, так и в артиллерийской практике для упрочнения стволов мощных орудий.
В результате натяга в трубах возникают нормальные напряжения, которые частично компенсируют напряжения в трубе от действия высокого давления.
Составные цилиндры. Автофретирование. Общие положения
Из формул (8.14) и (8.15) следует, что при действии только внутреннего давления напряжения в любых точках цилиндра положительны и по абсолютной величине больше напряжений . Наибольшего значения напряжения достигают у точек внутренней поверхности цилиндра, где они равны
В остальных точках напряжения меньше этого значения.
Наибольшее значение можно уменьшить путем применения составных толстостенных цилиндров, состоящих из более тонких труб, надетых друг на друга. При этом наружная труба изготавливается с внутренним диаметром, несколько меньшим наружного диаметра внутренней трубы. Разница между этими диаметрами до сборки принимается до изготовления и называется натягом.
Чтобы соединить цилиндры наружный цилиндр обычно нагревают, он расширяется и появляется возможность одеть его на внутренний цилиндр. Возможно такое охлаждение внутреннего цилиндра в жидком азоте или запрессовка цилиндров друг в друга. После сборки выравнивается температура, наружный цилиндр плотно охватывает внутренний и получается надежное соединение.
В результате натяга в трубах возникают начальные напряжения, причем, чем больше величина натяга, тем больше начальные напряжения.
Способ уменьшения напряжений и, как следствие, повышение прочности толстостенных цилиндров путем замены сплошного цилиндра составным был предложен академиком А.В.Гадолиным.
Обозначим через b и c радиусы наружного цилиндра, через a и b+∆/2 радиусы внутреннего цилиндра, а ∆ — натяг (см. рис.9).
Рис.9
При одинаковой длине соединенных цилиндров контактное давление pk равномерно распределено по посадочной поверхности.
Подставив в формулы(8.14) и (8.15) параметры, характеризующие напряжения в наружном цилиндре получим
Аналогично можно определить напряжения, возникающие на посадочной поверхности внутреннего цилиндра
Если внутренний и наружный цилиндры изготовлены из одного и того же материала, то контактное давление pk определяется зависимостью
где Е – модуль упругости материала внутреннего и наружного цилиндров.
За счет натяга в составном цилиндре возникают начальные напряжения, характер изменения которых по наружному сечению показан на рис.10.
Рис.10Рис.11
При приложении внутреннего рабочего давления на начальные напряжения накладываются рабочие напряжения (показываются на рис.11 пунктиром). Суммарные напряжения показаны на рис.11.
В точках, расположенных на внутренней поверхности составного цилиндра, суммарное окружное напряжение получается меньше, чем в тех же точках целого цилиндра.
Оптимальное значение натяга можно определить из условия равнопрочности внутреннего и наружного цилиндров, оптимальное значение радиуса контактной поверхности – из условия наибольшего снижения эквивалентного напряжения в опасной точке.
В соответствии с этим оптимальный радиус контактной поверхности:
Натяг соответствующий этому радиусу и внутреннему давлению pв:
Необходимо отметить, что детали, предназначенные для соединения с натягом, должны изготавливаться с большой точностью, т.к. даже небольшое отклонение от номинальной величины натяга может привести к снижению прочности соединения.
В технике высоких давлений, кроме посадки, применяется так называемое автофретирование, которое заключается в предварительной нагрузке цилиндра внутренним давлением, больше рабочего, с таким расчетом, чтобы во внутренних слоях цилиндра возникали пластические деформации. После снятия давления во внешних слоях цилиндра сохраняются упругие напряжения растяжения, а во внутренних слоях возникают деформации сжатия (см. рис.12).
В дальнейшем при нагрузке цилиндра давлением остаточные напряжения суммируются с рабочим так, что во внутренних слоях имеет место чистая разгрузка. Материал цилиндра не получает пластических деформаций, если только рабочее давление не превышает давление предварительного обжатия.
Рис.12
Постановка задачи.
В ходе работы необходимо провести расчет на прочность оболочки двигателя .Для этого работа разделяется на несколько этапов:
1. Построение 3D-модели в SolidWorks.
• Заготовка 3-d модели.
• Скругление элементов 3-d модели.
• Сохранение модели в формате, совместимости с ANSYS.
2. Работа с моделью в ANSYS.
• Импортирование сохраненного файла.
• Задание материала конструкции
• Конечно-элементное разбиение модели
• Приложение экспериментальных нагрузок
3. Обсуждение результатов.
Создание детали.
Открываем программу SolidWorks, выбираем вид спереди, вставляем эскиз и строим нашу модель. Чтобы получить нашу деталь, выбираем команду «Повернутая бобышка/основание», указываем ось вращения и наш эскиз и крутим на 360 градусов (Рис.13)
Рис.13 Заготовка 3-d модели.
В получившейся заготовке делаем скругление элементов заготовки , с помощью команды «Скругление» (Рис.14)
Рис.14 Скругление элементов заготовки.
Решение задачи в ANSYS
4.1. Создание материала
Открываем программу ANSYS Workbench. При помощи мышки вытаскиваем окно Static Structural. Это окно содержит пункты: библиотека, геометрия, разбиение, результаты и др.
Рис.14. Окно Static Structural
В этом окне двойным щелчком мыши по Engineering Data открываем библиотеку материалов и выбираем материал Aluminum Alloy. 
Рис. 15. Библиотека материалов
Загружаем нашу модель построенную в Solid Works в ANSYS Workbench, для этого правой клавишей нажимаем в окне Static Structural на Geometry.
Рис. 16. Выбор геометрии
После открываем нашу геометрию, нажимаем на Generate и получаем нашу модель.
Рис. 17. Модель оболочки двигателя после импорта в ANSYS
4.2. Приложение нагрузок и результаты
Чтобы получить более точные результаты расчетов, разбиваем модель изолятора на конечные элементы. Для этого открываем пункт Model. Затем в дереве построений нажимаем правой клавишей на Mesh, затем на Generate Mesh.
Для того чтобы задать размер разбиения в команде Mesh Control выбираем Sizing. Параметры Sizing позволяют изменить плотность сетки отдельной детали, увеличить или уменьшить размер элементов относительно параметров, заданных глобально. В результате всех операций получаем разбиение оболочки двигателя .
Рис. 18.Конечная–элементная сетка.
Качество сетки хорошее это обусловлено геометрией модели и методом разбиения.
4.3 Нахождение максимальных деформаций
Данный расчет будет проведен для материала алюминий . В дереве построения выбираем вкладку Geometry и выбираем материал Aluminum Alloy. Следующим шагом является создание закреплений.
Командой Fixed Support задаем жесткую заделку. Модель становится закрепленной и становится возможным приложение нагрузки.
В дереве построения выбираем команду Static Structural→ Loads→ Force.
Нагрузку, равную 50 МПа., мы будем прикладывать к верхней части оболочки. Выбираем в дереве построения вкладку Solution и выбираем пункт Deformation→Total Deformation. Выбираем нашу модель и нажимаем команду Solve для расчетов. И получаем диаграмму деформаций элерона (рис.19).
Рис.19. Деформация элемента оболочки
Диаграмма показывает максимальные деформации красным цветов, на оболочке они возникают в самой верхней части . Максимальная деформация равна 0,28 мм.
📸 Видео
Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать
Система уравнений. Метод алгебраического сложенияСкачать
Системы уравнений 7-11 класс. Вебинар | МатематикаСкачать
Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать
Сопротивление материалов. Лекция: тонкостенные оболочки вращения (исправленное видео)Скачать
МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать
7 класс, 39 урок, Метод алгебраического сложенияСкачать
Решение систем уравнений методом сложенияСкачать
СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать
МЕТОД АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ II #математика #егэ #shorts #профильныйегэСкачать
Системы уравнений Тема5 Решения задач составлением системы уравнений.Скачать
Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать
Урок по теме ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ 7 КЛАСССкачать
Система уравнений с модулями #1Скачать
Графический метод решения задачи линейного программирования (ЗЛП)Скачать
Базисные решения систем линейных уравнений (03)Скачать
Решение системы линейных уравнений с двумя переменными способом сложения. 6 класс.Скачать
