Привет, Хабр! Некоторое время назад увлекся глубоким обучением и стал потихоньку изучать tensorflow. Пока копался в tensorflow вспомнил про свою курсовую по параллельному программированию, которую делал в том году на 4 курсе университета. Задание там формулировалось так:
Линейная начально-краевая задача для двумерного уравнения теплопроводности:
Хотя правильнее было бы назвать это уравнением диффузии.
Задачу тогда требовалось решить методом конечных разностей по неявной схеме, используя MPI для распараллеливания и метод сопряженных градиентов.
Я не специалист в численных методах, пока не специалист в tensorflow, но опыт у меня уже появился. И я загорелся желанием попробовать вычислять урматы на фреймворке для глубокого обучения. Метод сопряженных градиентов реализовывать второй раз уже не интересно, зато интересно посмотреть как с вычислением справится tensorflow и какие сложности при этом возникнут. Этот пост про то, что из этого вышло.
Видео:Решение уравнения теплопроводности методом конечных разностейСкачать
Численный алгоритм
Разностная схема:
Чтобы проще было расписывать, введем операторы:
Явная разностная схема:
В случае явной разностной схемы для вычисления используются значения функции в предыдущий момент времени и не требуется решать уравнение на значения . Однако такая схема менее точная и требует значительно меньший шаг по времени.
Неявная разностная схема:
Перенесем в левую сторону все связанное с , а в правую и домножим на :
По сути мы получили операторное уравнение над сеткой:
что, если записать значения в узлах сетки как обычный вектор, является обычной системой линейных уравнений (). Значения в предыдущий момент времени константы, так как уже рассчитаны.
Для удобства представим оператор как разность двух операторов:
Заменив на нашу оценку , запишем функционал ошибки:
где — ошибка в узлах сетки.
Будем итерационно минимизировать функционал ошибки, используя градиент.
В итоге задача свелась к перемножению тензоров и градиентному спуску, а это именно то, для чего tensorflow и был задуман.
Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать
Реализация на tensorflow
Кратко о tensorflow
В tensorflow сначала строится граф вычислений. Ресурсы под граф выделяются внутри tf.Session. Узлы графа — это операции над данными. Ячейками для входных данных в граф служат tf.placeholder. Чтобы выполнить граф, надо у объекта сессии запустить метод run, передав в него интересующую операцию и входные данные для плейсхолдеров. Метод run вернет результат выполнения операции, а также может изменить значения внутри tf.Variable в рамках сессии.
tensorflow сам умеет строить графы операций, реализующие backpropagation градиента, при условии, что в оригинальном графе присутствуют только операции, для которых реализован градиент (пока не у всех).
Сначала код инициализации. Здесь производим все предварительные операции и считаем все, что можно посчитать заранее.
По-хорошему надо было считать значения функции на краях заданными и оптимизировать значения функции только во внутренней области, но с этим возникли проблемы. Способа сделать оптимизируемым только часть тензора не нашлось, и у операции присвоения значения срезу тензора не написан градиент (на момент написания поста). Можно было бы попробовать хитро повозиться на краях или написать свой оптимизатор. Но и просто добавление разности на краях значений функции и краевых условий в функционал ошибки хорошо работает.
Стоит отметить, что метод с адаптивным моментом показал себя наилучшим образом, пусть функционал ошибки и квадратичный.
Вычисление функции: в каждый момент времени делаем несколько оптимизационных итераций, пока не превысим maxiter или ошибка не станет меньше eps, сохраняем и переходим к следующему моменту.
Запуск:
Видео:Решение уравнения теплопроводности в одномерной постановке в Excel с применением неявной схемыСкачать
Результаты
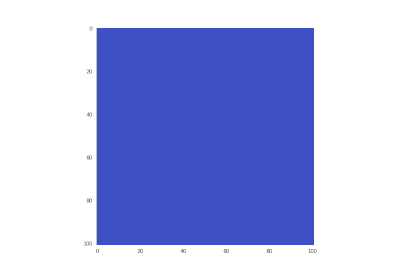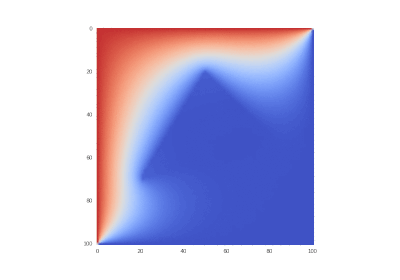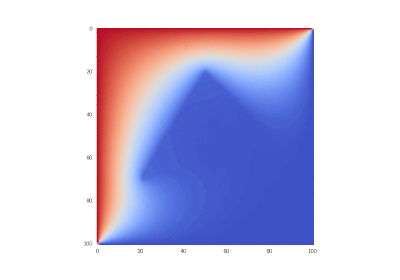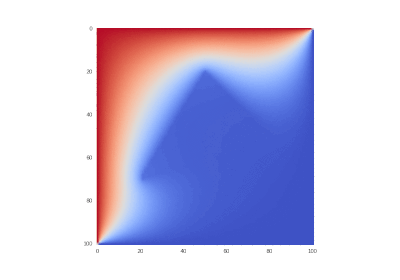
Условие как и оригинальное, но без в уравнении:
Что легко правится в коде:
Разницы почти нет, потому что производные имеют большие порядки, чем сама функция.
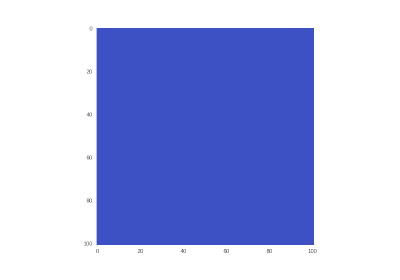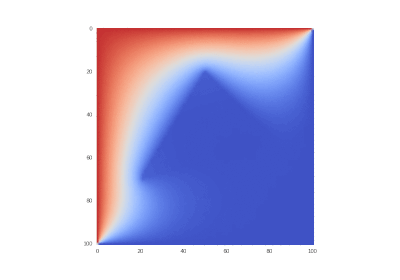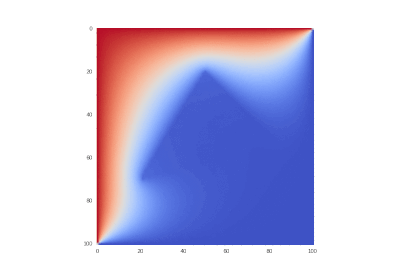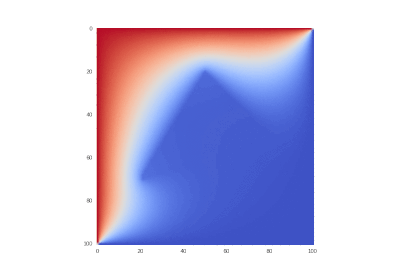
Условие с одним нагревающимся краем:
Условие с остыванием изначально нагретой области:
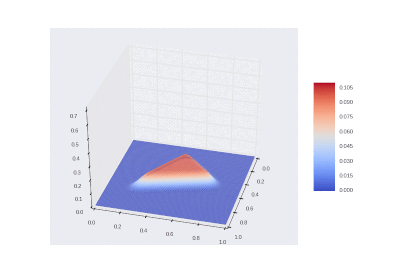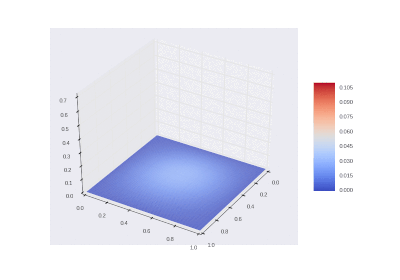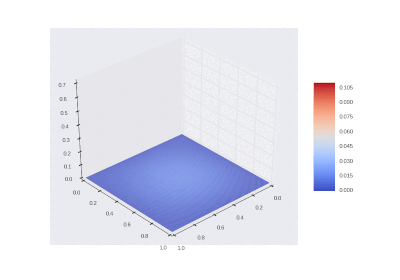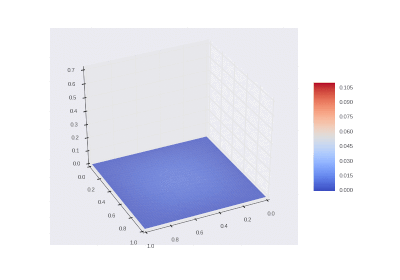
Условие с включением нагрева в области:
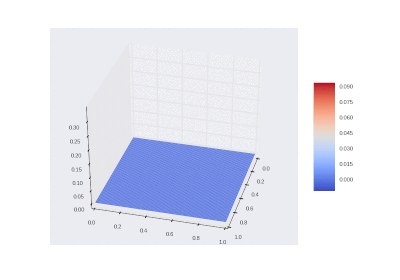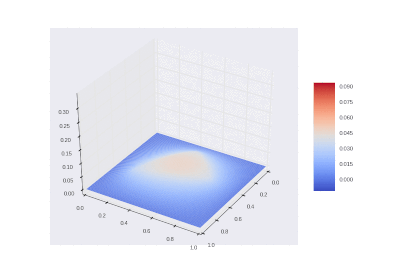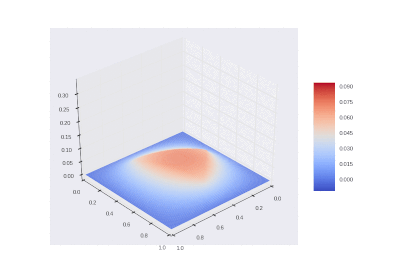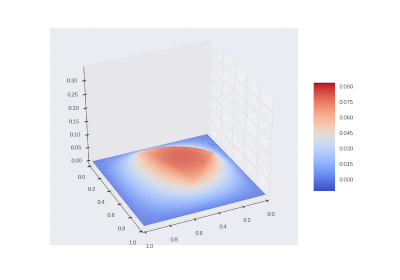
Видео:Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать
Рисование гифок
Функция рисования 3D-гифки:
В основной класс добавляем метод, возвращающий U в виде pandas.DataFrame
Функция рисования 2D-гифки:
Стоит отметить, что оригинальное условие без использования GPU считалось 4м 26с, а с использованием GPU 2м 11с. При больших значениях точек разрыв растет. Однако не все операции в полученном графе GPU-совместимы.
- Intel Core i7 6700HQ 2600 МГц,
- NVIDIA GeForce GTX 960M.
Посмотреть, какие операции на чем выполняются, можно с помощью следующего кода:
Это был интересный опыт. Tensorflow неплохо показал себя для этой задачи. Может быть даже такой подход получит какое-то применение — всяко приятнее писать код на питоне, чем на C/C++, а с развитием tensorflow станет еще проще.
Видео:Решение нестационарного уравнения теплопроводности в двухмерной постановке в ExcelСкачать
Решение уравнения теплопроводности с помощью python (NumPy)
Я решаю уравнение теплопроводности для металлического стержня, поскольку один конец поддерживается при 100 ° C, а другой при 0 ° C как
Если изменение граничного условия Неймана как одного конца изолировано (а не флюсом),
то как расчетный термин
Типичный подход к граничному условию Неймана состоит в том, чтобы представить «точку-призрак» на один шаг за пределами области и вычислить значение для нее с использованием граничного условия; затем выполните нормально (используя PDE) для точек, находящихся внутри сетки, включая границу Неймана.
Точка призрака позволяет использовать симметричную конечную разностную аппроксимацию производной на границе, т.е. (T[n, j+1] — T[n, j-1])/(2*dy) если y — пространственная переменная. Несимметричная аппроксимация (T[n, j] — T[n, j-1])/dy , которая не содержит точки призрака, намного менее точна: введенная ошибка на порядок хуже ошибки участвующих в дискретизации самого PDE.
Итак, когда j является максимальным возможным индексом для T, граничное условие говорит, что » T[n, j+1] » следует понимать как T[n, j-1] и это то, что делается ниже.
Видео:Уравнение в частных производных Уравнение теплопроводностиСкачать
Рекомендация для метода конечных разностей в научном Python
Для проекта, над которым я работаю (в гиперболических PDE), я хотел бы получить некоторую приблизительную информацию о поведении, взглянув на некоторые цифры. Я, однако, не очень хороший программист.
Можете ли вы порекомендовать некоторые ресурсы для изучения того, как эффективно кодировать конечно-разностные схемы в Scientific Python (другие языки с небольшой кривой обучения также приветствуются)?
Чтобы дать вам представление об аудитории (я) по этой рекомендации:
- Я чистый математик по образованию, и я немного знаком с теоретическими аспектами конечно-разностных схем
- Мне нужна помощь в том, чтобы заставить компьютер вычислять то, что я хочу вычислить, особенно таким образом, чтобы я не дублировал слишком много усилий, уже приложенных другими (чтобы не заново изобретать колесо, когда пакет уже доступен). (Другая вещь, которую я хотел бы избежать, — это глупо кодировать что-то вручную, когда существуют установленные структуры данных, соответствующие цели.)
- У меня был некоторый опыт кодирования; но у меня не было ни одного в Python (поэтому я не против, если есть хорошие ресурсы для изучения другого языка [скажем, например, Octave]).
- Книги, документация были бы полезны, как и коллекции примеров кода.
📹 Видео
#5. Математические функции и работа с модулем math | Python для начинающихСкачать
Использование библиотеки SymPy для работы с системами уравнений в PythonСкачать
Python - численное решение дифференциального уравнения 1го порядка и вывод графикаСкачать
Основы SciPy | Научные И Математические Вычисления На PythonСкачать
Разностные схемы для решения уравнения переноса. Numerical Schemes for Linear Advection Equation.Скачать
Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать
Решение задачи Коши для уравнения теплопроводности (Часть 1)Скачать
Python с нуля. Урок 18 | Вложенные функции, замыканияСкачать
#44. Замыкания в Python | Python для начинающихСкачать
Решение задачи теплопроводности (Явная разностная схема)Скачать
Методы решения уравнения теплопроводности с несколькими пространственными переменнымиСкачать
Одномерное уравнение теплопроводности. Виды краевых задачСкачать
Решение уравнения теплопроводности методом клеточных автоматов.Скачать
Динамическое программирование. Часть 1. Одномерная динамика. Код на PythonСкачать
