Читайте также:
|
Важную роль в системах обработки сигналов играют рекурсивные фильтры 1-го и 2-го порядков.
• Базовый рекурсивный фильтр 1-го порядка. Базовым РФ 1-го порядка называют фильтр, описываемый разностным уравнением вида:
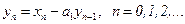
Применив z-преобразование к левой и правой частям уравнения, получим
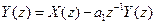
Следовательно, передаточная функция фильтра имеет вид

• Рекурсивный фильтр 1-го порядка. Разностное уравнение имеет вид:
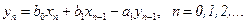
Применив z-преобразование к левой и правой частям уравнения, получим
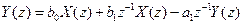

• Базовый рекурсивный фильтр 2-го порядка.Разностное уравнение и передаточная функция имеют вид:
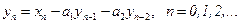
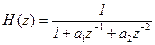
• Рекурсивный фильтр 2-го порядка. Разностное уравнение и передаточная Функция имеют вид:

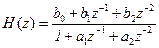
• Нерекурсивный фильтр 2-го порядка. Разностное уравнение и передаточная функция имеют вид:
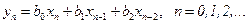
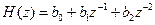
На основе приведенных примеров можно сформулировать мнемоническое правило определения передаточной функции по разностному уравнению (и наоборот):
• коэффициенты разностного уравнения являются коэффициентами передаточной функции;
• коэффициенты разностного уравнения 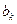

• коэффициенты разностного уравнения bk при xn—k равны коэффициентам знаменателя передаточной функции (с обратным знаком) при z — k , k = О, 1. N
Пример. Известна передаточная функция рекурсивного фильтра
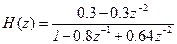
Разностное уравнение имеет вид:

• В общем случае передаточная функция дискретного фильтра может быть получена путем применения z-преобразования к разностным уравнениям (1) и (2). Рекурсивный фильтр:
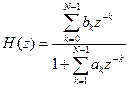
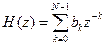
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)
Видео:Основы ЦОС: 23. Цифровые фильтры (ссылка на скачивание скриптов в описании)Скачать

Разностное уравнение нерекурсивного цифрового фильтра


21.6. ЦИФРОВЫЕ ФИЛЬТРЫ, ИХ РАЗНОСТНЫЕ УРАВНЕНИЯ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ИМПУЛЬСНЫЕ ХАРАКТЕРИСТИКИ
Цифровой фильтр описывается тремя характеристиками разностным уравнением , которому может быть поставлена в соответствие передаточная функция K ( z ) или полученная в результате обратного z -преобразования K ( z ) его дискретная импульсная характеристика h [ k ] . Из приведенных примеров следует, что существуют два принципиально различных класса цифровых фильтров. Фильтры первого класса нерекурсивные описываются разностным уравнением, в котором выходная величина y [ k ] выражается только через конечное число значений входного сигнала x [ n ] . Таким, например, является уравнение усреднения, рассмотренное выше.
Фильтры второго класса рекурсивные описываются уравнением, в котором выходная переменная y [ k ] выражается не только через значения входного сигнала x [ n ], но и через предшествующие значения выходного сигнала y [ k – m ] . Сюда, например, относится разностное уравнение u2[ k + 1] = u2[ k ] e -T/ t + u1[ k ][h(T) – h(T – Tи)], описывающее преобразование прямоугольных сигналов RС -цепью (см. п. 20.4), а также дискретные модели любых других аналоговых динамических систем (в частности, электрических цепей).
Нерекурсивный цифровой фильтр сохраняет информацию о входном сигнале за конечное число шагов его импульсная характеристика конечна, а передаточная функция имеет вид ряда по степеням z (который включает и отрицательные показатели).
Информация, поступившая на вход рекурсивного фильтра, сохраняется в нем бесконечно долго; он имеет бесконечную по длительности импульсную характеристику и описывается передаточной функцией в виде рациональной дроби. Максимальная разность индексов переменных в разностном уравнении, который отвечает разность степеней z в числителе и знаменателе передаточной функции, определяет порядок цифрового фильтра.
Так, нерекурсивный цифровой фильтр второго порядка описывается разностным уравнением f 2 [ n ] = a 0 f 1 [ n ] + a 1 f 1 [ n – 1] + a 2 f 1 [ n – 2], его передаточная функция K ( z ) = a 0 + a 1 z –1 + a 2 z –2 , а импульсная характеристика определяется коэффициентами, h [ n ] = a 0 , a 1 , a 2 , 0, 0, 0, 0, .
Рекурсивный цифровой фильтр второго порядка описывается разностным уравнением f 2 [ n ] = a 0 f 1 [ n ] + a 1 f 1 [ n – 1] + a 2 f 1 [ n – 2] + b 1 f 2 [ n – 1] + b 2 f 2 [ n – 2],
а его передаточная функция 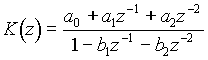
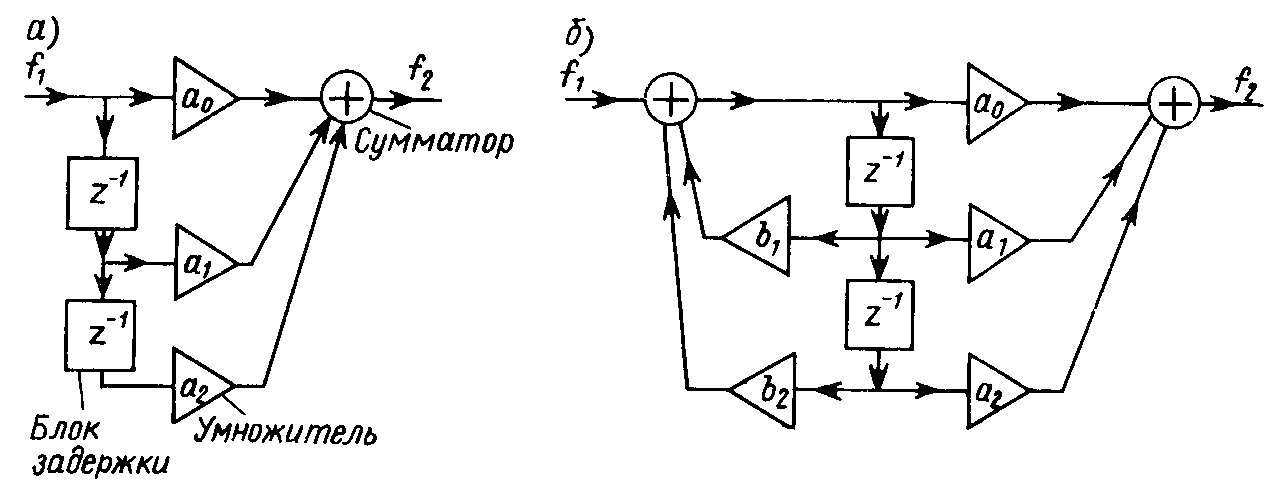
По известным значениям коэффициентов разностного уравнения a k и b k цифровой фильтр 2-го порядка может быть реализован с помощью умножителей, сумматоров и блоков задержки.
Блок-схемы цифровых фильтров обоих классов 2-го порядка, включающие перечисленные блоки, показаны на рис. 21.10 ( а – нерекурсивный; б – рекурсивный).
Видео:Основы ЦОС: 24. КИХ и БИХ фильтры (ссылка на скачивание скриптов в описании)Скачать

Разностное уравнение нерекурсивного цифрового фильтра
«Понятие цифровых фильтров»
Передаточная функция звена фильтра низкой частоты первого порядка, схема которого представлена на рис.8.1
 |
равна 
Этой передаточной функции соответствует дифференциальное уравнение, описывающее процессы в данном звене, которое имеет вид

Преобразуем данную непрерывную систему в дискретную установкой на входе и на выходе синхронных идеальных импульсных элементов, работающих с частотой f (рис.8.2).
 |
Дифференциальное уравнение непрерывной системы преобразуется в разностное уравнение дискретной системы заменой производной конечной разностью.

где 

преобразуем уравнение (8.3) к виду


придем к окончательному виду

Уравнение (8.7) представляет из себя разностное уравнение простейшего дискретного фильтра низких частот первого порядка.
В общем случае линейным дискретным фильтром называется дискретная система, удовлетворяющая линейному разностному уравнению

где x ( n ) и y ( n ) – соответственно входная и выходная последовательности устройства. Если хотя бы один коэффициент зависит от переменной n , то такой фильтр такой фильтр называется параметрическим или фильтром с переменными параметрами. Если все коэффициенты являются константами, то такой фильтр называется фильтром с постоянными коэффициентами.
Передаточная функция линейного дискретного фильтра имеет вид

который получается в результате применения z -преобразования к левой и правой частям уравнения (8.8).
Значения выходной последовательности y ( n ) определяются N значениями входного дискретного сигнала x ( n ) в моменты nT , ( n -1) T , ( n -2) T , и т.д. и M -1 значениями самого выходного дискретного сигнала в прошлые моменты ( n -1) T , ( n -2) T и т.д.
Фильтры, описываемые уравнением (8.8) называются рекурсивными.
В частном случае, при 

В этом случае значение выходного дискретного сигнала y ( n ) в любой момент nT определяется лишь значениями входного дискретного сигнала в этот же момент и N -1 его прошлыми значениями. Фильтры, описываемые уравнением (8.10) называются нерекурсивными. Передаточная функция нерекурсивного фильтра имет вид

Как видно из уравнения (8.8), в общем случае линейный дискретный фильтр может быть реализован путем комбинации операций умножения сигнала на константу, алгебраического сложения и задержки сигнала на один интервал дискретизации T . Для условного изображения алгоритмов дискретных фильтров используются структурные схемы, на которых вышеперечисленные операции изображаются так, как показано на рис.8.3.
 |
Для реализации дискретных фильтров наиболее часто используются следующие формы структурных схем.
Прямая форма структурной схемы рекурсивного фильтра, представленная на рис.8.4, реализуется непосредственно по разностному уравнению (8.8) или по передаточной функции (8.9).
 |
Эта схема содержим один сумматор, умножители и N + M -2 элементов задержки.
В качестве примера рассмотрим реализацию в прямой форме т.н. «биквадратного блока» – фильтра второго порядка, описываемого уравнением

или соответствующей передаточной функцией

Прямая форма структурной схемы биквадратного блока представлена на рис.8.5.
 |
Прямая каноническая форма содержит минимальное число элементов задержки. Она получается если передаточную функцию рекурсивного фильтра (8.9) представить в виде

где 
Передаточным функциям H 1 ( z ) и H 2 ( z ) соответствуют разностные уравнения

Так как в фильтрах, реализующих H 1 ( z ) и H 2 ( z ), имеет место только задержка сигнала v ( n ), то можно использовать только один набор элементов задержки. Прямая каноническая форма структурной схемы фильтра, описываемого уравнением (8.8) или соответствующей передаточной функцией (8.9) представлена на рис.8.6.
 |
Она содержит минимальное число элементов задержки 
Каскадная (последовательная) форма структурной схемы дискретного фильтра соответствует представлению передаточной фугкции (8.9) в виде произведения

где Hl ( z ) – передаточная функция биквадратного блока

где 
При этом отдельные биквадратные блоки, реализующие Hl ( z ) соединяются между собой последовательно. Такое представление всегда можно получить разложением числителя и знаменателя (8.9) на сомножители первого и второго порядка. Так что возможно, что в некоторых сомножителях Hl ( z ) некоторые коэффициенты равны нулю. При этом данные сомножители реализуются более простой структурой, чем показано на рис.8.5 и рис.8.7. Кроме того, при последовательном соединении биквадратных блоков, реализованных в прямой форме (рис.8.5), может оказаться, что элементы задержки в цепи обратной связи предшествующего блока дублируют элементы задержки в прямой ветви последующего блока. Поэтому при каскадной реализации L -звенного фильтра на биквадратных блоках в прямой форме из схемы могут быть исключены 2( L -1) элементов задержки.
Параллельная форма структурной схемы рекурсивного дискретного фильтра соответствует представлению передаточной функции (8.9) в виде

где слагаемые Hl ( z ) получаются при разложении H ( z ) на простые дроби типа

и могут быть реализованы в виде упрощенных структур биквадратных блоков.
Прямая форма структурной схемы нерекурсивного фильтра является непосредственной реализацией передаточной функции нерекурсивного фильтра (8.11) или его разностного уравнения (8.10). Прячмая форма, представленная на рис.8.8 содержит N -1 элементов задержки, N умножителей и сумматор на N входов.
 |
Эту форму называют также трансверсальным фильтром или фильтром с многоотводной линией задержки.
Каскадная (последовательная) форма структурной схемы нерекурсивного фильтра соответствует представлению передаточной функции (8.11) в виде произведения

где
или
Такое разложение всегда можно получить разложением H ( z ) на сомножители первого и второго порядка, каждый из которых реализуется с помощью упрощенной структуры биквадратного блока, а все составляющие блоки соединяются между собой последовательно.
Важнейшей временной характеристикой линейной дискретной системы является импульсная характеристика, под которой понимают реакцию системы h ( n ) на единичный импульс d ( n ) при нулевых начальных условиях. Импульсную характеристику можно расчитать путем решения соответствующего разностного уравнения дискретной системы.
В качестве примера вычислим импульсную характеристику дискретного линейного фильтра, описываемого разностным уравнением 
Входной дискретный сигнал фильтра x ( n ) можно представить в виде

Так как реакция дискретного фильтра на единичный импульс есть импульсная характеристика h ( n ), то вследствие стационарности фильтра реакцией фильтра на d ( n — m ) будет h ( n — m ). Тогда, вследтсвие линейности фильтра реакцией на вхожную последовательность x ( n ) будет

Заменой переменных это выражение может быть приведено к виду

При этом предполагается, что h ( n )=0 при n x ( n )=0 при n

Последняя формула определяет реакцию линейного дискретного фильтра на произвольное входное воздействие как свертку этого входного воздействия и импульсной характеристики.
Согласно формуле (8.25) переходная характеристика линейного дискретного фильтра т.е. его реакция на единичную последовательность при нулевых начальных условиях, может быть вычислена как

В свою очередь, очевидно, что

Если на вход линейного дискретного фильтра подается сигнал x ( n )= d ( n ), то реакцией системы будет y ( n )= h ( n ). При этом z -преобразования обоих сигналов будут иметь вид X ( z )=1, Y ( z )= H ( z ). Тогда передаточная функция фильтра

Это означает, что передаточная функция линейного дискретного фильтра есть ни что иное как z -преобразование импульсной характеристики. Если записать передаточную функцию в виде

то видно, что коэффициенты bk совпадают с k -ми выборками импульсной характеристики и следовательно

Таким образом, импульсную характеристику можно вычислить как обратное z -преобразование передаточной функции.
Фильтром с конечной импульсной характеристикой (КИХ-фильтром) называется фильтр, у которого импульсная характеристика представляет собой конечный дискретный сигнал, т.е. может принимать отличные от нуля значения лишь при n =0, 1, …, N -1.
Фильтром с бесконечной импульсной характеристикой (БИХ-фильром) называется фильтр, у которого импульсная характеристика может принимать отличные от нуля значения на бесконечном множестве значений n =0, 1, …
Нерекурсивный фильтр всегда является КИХ-фильтром, в то время как рекурсивный фильтр может быть как КИХ так и БИХ фильтром.
Линейный дискретный фильтр физически реализуем, если его выходной сигнал не опережает входного, т.е. в любой момент n выходной сигнал y ( n ) зависит лишь от значений входного сигнала в моменты, предшествующие n и не зависит от его значений в последующие моменты. Критерием физической реализуемости линейного дискретного фильтра является равенство нулю отсчетов импульсной характеристики при отрицательных значениях моментов отсчетов, т.е. h ( n )=0 при n
Фильтр называется устойчивым, если при любых начальных условиях реакция фильтра на любое ограниченное воздействие x ( n ) также ограничена, т.е. если 



Значит, критерием устойчивости дискретного фильтра является абсолютная сходимость ряда отсчетов импульсной характеристики.

Можно показать, что условие (8.32) является не только достаточным но и необходимым условием устойчивости фильтра. Однако неопсредственное использование этого условия для проверки устойчивости практически затруднено. Поэтому рассмотрим другую формулировку критерия устойчивости. Если представить передаточную функцию фильтра в общем виде (8.30), то можно сделать вывод о том, что

Если 

Это значит, что в устойчивом фильтре H ( z ) конечна во всех точках z -плоскости, где 

Найдем преобразования Фурье входного и выходного сигнала линейного дискретного фильтра

Здесь суммирование производится от n =0 так как предполагается, что x ( n )=0 и y ( n )=0 при n
Частотной характеристикой дискретного фильтра называется отношение

частотная характеристика совпадает с передаточной функцией на единичной окружности z -плоскости, т.е. при 

а для нерекурсивного фильтра

В общем случае H ( e j w T ) – комплексная функция, которая может быть записана в виде

где A ( w ) – модуль частотной характеристики – амплитудно-частотная характеристика (АЧХ), j ( w ) – аргумент частотной характеристики – фазочастотная характеристика (ФЧХ), R ( w )= A ( w ) cos j ( w ), J ( w )= A ( w ) sin j ( w ) – вещественная и мнимая части частотной характеристики. Производная от ФЧХ

называется групповым временем замедления (ГВЗ).
Из теории дискретных систем вытекают ряд важных свойств частотных характеристик линейных дискретных фильтров.
1. Все частотные характеристики дискретных фильтров являются непрерывными периодическими функциями частоты с периодом w d =2 p / T .
2. Для вещественных фильтров, т.е. фильтров, передаточные функции которых имеют только вещественные коэффициенты, АЧХ A ( w ) и ГВЗ t ( w ) представляют собой четные функции частоты, а ФЧХ j ( w ) – нечетную функцию частоты.
Из этого следует, что требования к частотным характеристикам достаточно задавать лишь на интервале полупериода 
Под цифровым фильтром понимают дискретный фильтр, описываемый уравнением (8.8) и реализованный программным путем с помощью микропроцессора или аппаратным путем в виде специализированного цифрового вычислительного устройства, состоящего из элементов памяти (регистров), сумматоров, умножителей и устройств управления.
Сигналы на входе и на выходе цифрового фильтра являются цифровыми, т.е. последовательностями чисел. Каждое из этих чисел представляется в виде двоичного кода определенной конечной разрядности. В цифровом фильтре в соответствии с алгоритмом (8.8) выполняются операции пересылки, сложения и умножения кодов. При этом алгоритм функционирования (8.8) реализуется неточно. Ошибки цифровой фильтрации обусловлены, во-первых, квантованием входных и выходных сигналов, во-вторых, квантованиемкоэффициентов фильтра и, в-третьих, конечной разрядностью операционных устройств, вследствие чего имеет место округление результатов арифметических операций. Таким образом, выбранная структура цифрового фильтра, разрядность входных и выходных сигналов, разрядность арифметических устройств влияют на точность работы устройства идолжны выбираться таким образом, чтобы результирующая ошибка цифрового фильтра не превышала допустимой величины.
Другим важным критерием качества цифрового фильтра является его быстродействие, определяемое минимальным временем, необходимым для вычисления одного отсчета выходного сигнала. Очевидно, что это время должно быть не больше периода дискретизации сигналов.
Цифровые фильтры могут иметь свойства как КИХ так и БИХ фильтров. В обоих случаях фильтры имеют свои преимущества и недостатки.
Преимущества КИХ фильтров:
1. КИХ фильтры могут иметь линейную ФЧХ.
2. КИХ фильтры, реализованные по нерекурсивному алгоритму всегда устойчивы.
3. Для КИХ фильтров, реализованных по нерекурсивному алгоритму шумы квантования можно сделать приемлемо малыми.
4. КИХ фильтры могут быть реализованы по рекурсивному алгоритму, если это необходимо.
Недостатки КИХ фильтров:
1. Длительность импульсной характеристики КИХ фильтра, несмотря на то, что она конечна, может оказаться достаточно большой для достижения резкого спада частотной характеристики на границе зоны пропускания.
2. Разработка КИХ фильтров более сложна чем разработка БИХ фильтров с аналогичными характеристиками.
Преимущества БИХ фильтров:
1. БИХ фильтры могут быть использованы для реализации цифровых аналогов классических видов аналоговых фильров, таких как фильтры Баттерворта, Чебышева и т.д.
2. При аналогичных характеристиках, БИХ фильтры имеют более простую реализацию по сравнению с КИХ фильтрами.
Недостатки БИХ фильтров:
1. БИХ фильтры более чувствительны к конечной разрядности вычислений, которая приводит у них к появлению колебаний т.н. «предельных циклов».
2. За исключением специального случая, когда все полюса передаточной функции лежат на единичной окружности z -плоскости, невозможно построить реализуемый стабильный БИХ фильтр, имеющий точно линейную ФЧХ.
🎦 Видео
С чего начать цифровые фильтрыСкачать

Уроки Arduino. Фильтры данных, обработка сигналовСкачать

Цифровая обработка сигналов ФильтрыСкачать

ЦОС в РЗиА. Цифровые фильтры Часть 1. Банных П. Ю.Скачать

Цифровые фильтры LabVIEW / ОсновыСкачать

ЦОС 4 Цифровые фильтры БИХ и КИХСкачать

Введение в цифровую обработку сигналов. Ч. 3. Цифровые фильтры Ч.4. Цифровая обработка сигналов и MLСкачать

Цифровые фильтры - основы, принципы, примерыСкачать

Семинар по ЦОС: Проектирование КИХ-фильтра с помощью FilterDesignerСкачать

Семинар по ЦОС: Проектирование КИХ-фильтраСкачать

4_4 Метод чебышевской аппроксимации для синтеза КИХ-фильтровСкачать

Основы ЦОС: 18. Преобразование Фурье (ссылки на скачивание скриптов в описании)Скачать

Что такое КИХ-фильтр?Скачать

МАТЕМАТИЧЕСКИЕ МЕТОДЫ ТЕОРИИ СИГНАЛОВ И СИСТЕМ. Лекция 15. Линейные фильтры. Лектор Хохлов Н.А.Скачать

2020Весна ЦОС Схемы фильтров, устойчивость, синтез фильтровСкачать

ЦОС в РЗиА Цифровые фильтры Часть 5 Апросин К ИСкачать

Радиотехнические цепи и сигналы. Лекция №19-20 (04.12.2021) [5 семестр]Скачать
![Радиотехнические цепи и сигналы. Лекция №19-20 (04.12.2021) [5 семестр]](https://i.ytimg.com/vi/F5U4V1LTeak/0.jpg)