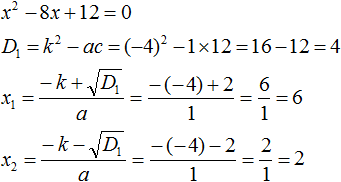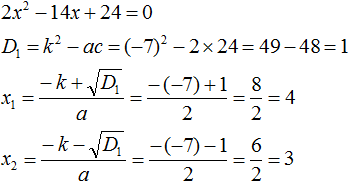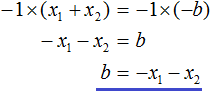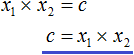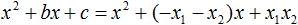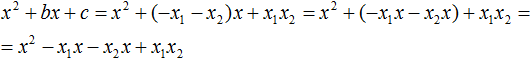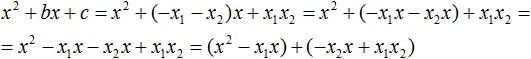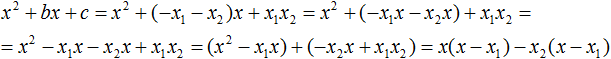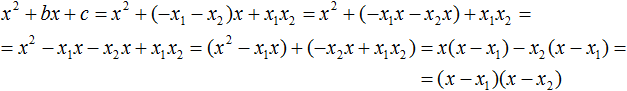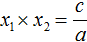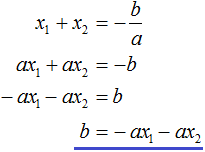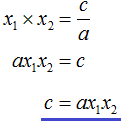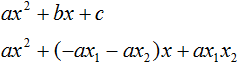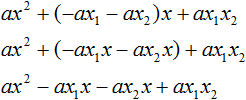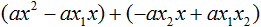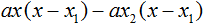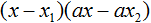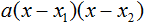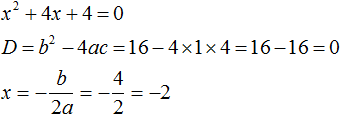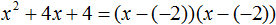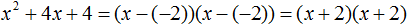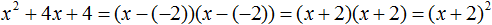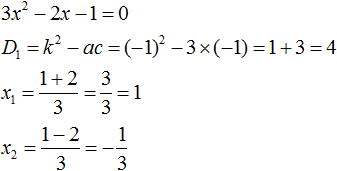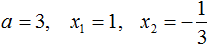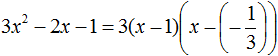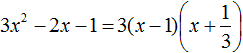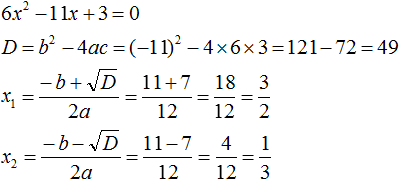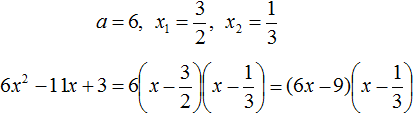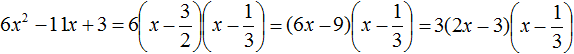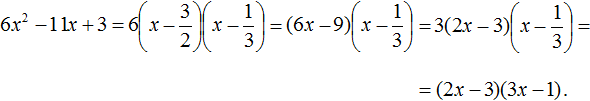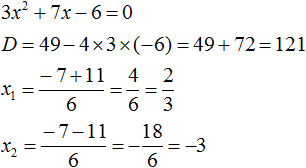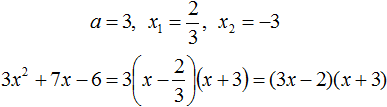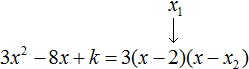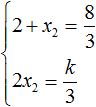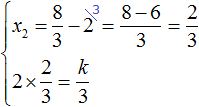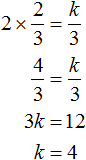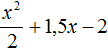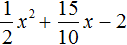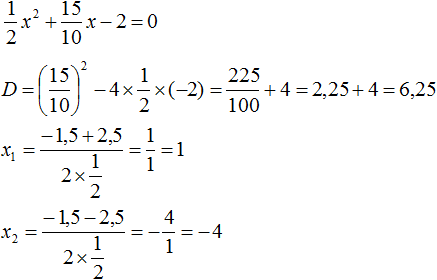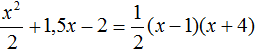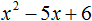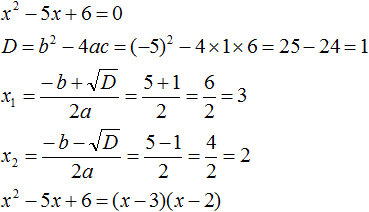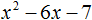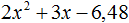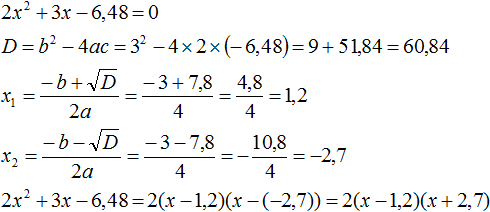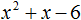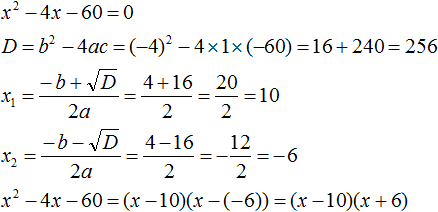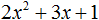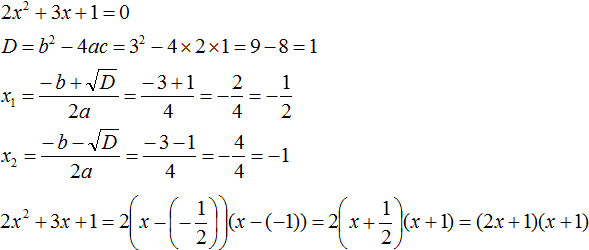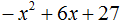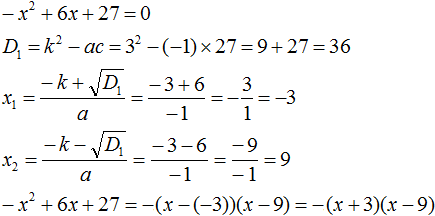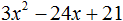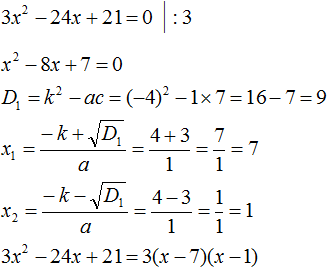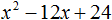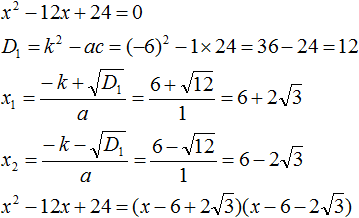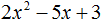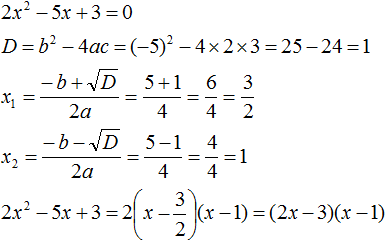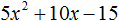Разложить квадратное уравнение на множители без дискриминанта (4 видео)

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Содержание

Калькулятор онлайн. Выделение квадрата двучлена и разложение на множители квадратного трехчлена.
Разложение квадратного трёхчлена на множители
Как разложить на множители квадратный трёхчлен
Как это работает
Примеры разложений
Задания для самостоятельного решения
Методика разложения квадратного уравнения на множители
Общие сведения
Формулы разложения на элементы
Корни уравнения
Алгоритм операции
Примеры решения
📺 Видео

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Калькулятор онлайн.
Выделение квадрата двучлена и разложение на множители квадратного трехчлена.

Т.е. задачи сводятся к нахождению чисел ( p, q ) и ( n, m )

Программа не только даёт ответ задачи, но и отображает процесс решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода квадратного трехчлена, рекомендуем с ними ознакомиться.

В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x — 3,5x^2

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 — 5&6/5x +1/7x^2
Результат: ( 3frac — 5frac x + fracx^2 )

При вводе выражения можно использовать скобки. В этом случае при решении введённое выражение сначала упрощается.
Например: 1/2(x-1)(x+1)-(5x-10&1/2)

Видео:Разложение квадратного трехчлена на множители. 8 класс.Скачать

Разложение квадратного трёхчлена на множители

Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Как разложить на множители квадратный трёхчлен

Квадратный трёхчлен — это многочлен вида ax 2 + bx + c .

В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так:

Левая часть этого уравнения является квадратным трёхчленом.

Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена.

Полученные корни x₁ и x₂ следует подстáвить в следующее выражение, которое и станет разложением:

Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой:

Где левая часть — исходный квадратный трёхчлен.

Пример 1. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение:

В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:

Итак, x₁ = 6 , x₂ = 2 . Теперь воспользуемся формулой ax 2 + bx + c = a(x − x₁)(x − x₂). В левой части вместо выражения ax 2 + bx + c напишем свой квадратный трёхчлен x 2 − 8x + 12. А в правой части подставим имеющиеся у нас значения. В данном случае a = 1, x₁ = 6, x₂ = 2

Если a равно единице (как в данном примере), то решение можно записать покороче:

Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства.

Раскроем скобки у правой части равенства, то есть в выражении (x − 6)(x − 2) . Если мы всё сделали правильно, то должен получиться квадратный трёхчлен x 2 − 8x + 12

Пример 2. Разложить на множители следующий квадратный трёхчлен:

Приравняем данный квадратный трёхчлен к нулю и решим уравнение:

Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:

Итак, x₁ = 4 , x₂ = 3 . Приравняем квадратный трехчлен 2x 2 − 14x + 24 к выражению a(x − x₁)(x − x₂) , где вместо переменных a , x₁ и x₂ подстáвим соответствующие значения. В данном случае a = 2

Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x 2 − 14x + 24

Видео:Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Как это работает

Разложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить тождественные преобразования.

Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице:

Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:

Тогда приведённый квадратный трехчлен x 2 + bx + c можно разложить на множители следующим образом. Сначала выразим b из уравнения x₁ + x₂ = −b . Для этого можно умножить обе его части на −1

Переменную c из теоремы Виета выражать не нужно — она уже выражена. Достаточно поменять местами левую и правую часть:

Теперь подставим выраженные переменные b и c в квадратный трёхчлен x 2 + bx + c

Раскроем скобки там где это можно:

В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:

Из первых скобок вынесем общий множитель x , из вторых скобок — общий множитель −x₂

Далее замечаем, что выражение ( x − x₁ ) является общим множителем. Вынесем его за скобки:

Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить.

Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a

Вспоминаем, что если квадратное уравнение не является приведённым, то есть имеет вид ax 2 + bx + c = 0 , то теорема Виета принимает следующий вид:

Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax 2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a

Далее чтобы квадратный трёхчлен вида ax 2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства 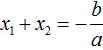и

Для начала выразим b и c . В первом равенстве умножим обе части на a . Затем обе части получившегося равенства умножим на −1

Теперь из второго равенства выразим c . Для этого умножим обе его части на a

Теперь подставим выраженные переменные b и с в квадратный трёхчлен ax 2 + bx + c . Для наглядности каждое преобразование будем выполнять на новой строчке:

Здесь вместо переменных b и c были подставлены выражения −ax₁ − ax₂ и ax₁x₂ , которые мы ранее выразили из теоремы Виета. Теперь раскроем скобки там где это можно:

Теперь из первых скобок вынесем общий множитель ax , а из вторых — общий множитель −ax₂

Далее замечаем, что выражение x − x₁ тоже является общим множителем. Вынесем его за скобки:

Вторые скобки содержат общий множитель a . Вынесем его за скобки. Его можно расположить в самом начале выражения:

Отметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители. Действительно, если не найдены корни квадратного трёхчлена, то нéчего будет подставлять в выражение a(x − x₁)(x − x₂) вместо переменных x₁ и x₂ .

Если квадратный трёхчлен имеет только один корень, то этот корень одновременно подставляется в x₁ и x₂ . Например, квадратный трёхчлен x 2 + 4x + 4 имеет только один корень −2

Тогда значение −2 в процессе разложения на множители будет подставлено вместо x₁ и x₂ . А значение a в данном случае равно единице. Её можно не записывать, поскольку это ничего не даст:

Скобки внутри скобок можно раскрыть. Тогда получим следующее:

При этом если нужно получить короткий ответ, последнее выражение можно записать в виде (x + 2) 2 поскольку выражение (x + 2)(x + 2) это перемножение двух сомножителей, каждый из которых равен (x + 2)

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Примеры разложений

Пример 1. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения. В левой части напишем квадратный трёхчлен 3x 2 − 2x − 1 , а в правой части — его разложение в виде a(x − x₁)(x − x₂) , где вместо a , x₁ и x₂ подстáвим соответствующие значения:

Во вторых скобках можно заменить вычитание сложением:

Пример 2. Разложить на множители следующий квадратный трёхчлен:

Упорядочим члены так, чтобы старший коэффициент располагался первым, средний — вторым, свободный член — третьим:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Упростим получившееся разложение. Вынесем за первые скобки общий множитель 3

Теперь воспользуемся сочетательным законом умножения. Напомним, что он позволяет перемножать сомножители в любом порядке. Умножим 3 на вторые скобки. Это позвóлит избавиться от дроби в этих скобках:

Пример 3. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Пример 4. Найдите значение k , при котором разложение на множители трёхчлена 3x 2 − 8x + k содержит множитель (x − 2)

Если разложение содержит множитель (x − 2) , то один из корней квадратного трёхчлена равен 2 . Пусть корень 2 это значение переменной x₁

Чтобы найти значение k , нужно знать чему равен второй корень. Для его определения воспользуемся теоремой Виета.

В данном случае квадратный трёхчлен не является приведённым, поэтому сумма его корней будет равна дроби , а произведение корней — дроби

Выразим из первого равенства переменную x₂ и сразу подстáвим найденное значение во второе равенство вместо x₂

Теперь из второго равенства выразим k . Так мы найдём его значение.

Пример 5. Разложить на множители следующий квадратный трёхчлен:

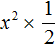
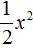
Перепишем данный трёхчлен в удобный для нас вид. Если в первом члене заменить деление умножением, то получим . Если поменять местами сомножители, то получится . То есть коэффициент a станет равным

Коэффициент b можно перевести в обыкновенную дробь. Так проще будет искать дискриминант:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Видео:ОГЭ математика. Задача 9. Решаем квадратное уравнение методом разложения на множителиСкачать

Задания для самостоятельного решения

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Видео:Математика - Разложение трехчлена на множителиСкачать

Методика разложения квадратного уравнения на множители

Нахождение дискриминанта не всегда оптимизирует процесс вычисления, поскольку занимает некоторое время. Однако существуют более верные методы решения квадратного уравнения. Разложение на множители — один из них, который не только ускорит нахождение корней, но и поможет при упрощении различных математических выражений, понижая их степень.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Общие сведения

Квадратное уравнение — математическое тождество, имеющее в своем составе неизвестную величину, которая возведена в квадрат. Специалисты еще называют его квадратным трехчленом вида Pt^2+St+U=0, где t — неизвестная величина (переменная), P и S — коэффициенты при переменных, а U — свободный член.

Однако формулы разложения квадратного трехчлена на множители не во всех случаях бывает эффективным. Чтобы это понимать, нужно рассмотреть классификацию этих уравнений. Они бывают двух типов:

К первому типу относятся тождества с полным набором коэффициентов и неизвестных, т. е. Pt^2+St+U=0. Их раскладывать на множители не рекомендуется. Если S или U эквивалентны нулевому значению, то выражения относятся ко второму виду. Иногда возможно одновременное равенство вышеописанных величин 0. В этом случае уравнение имеет такой вид: Pt^2=0. Однако по определению квадратного многочлена коэффициент при второй степени не может соответствовать 0, т. е. он не считается квадратным.

Неполные также можно классифицировать на два вида: без свободного члена и с его наличием. К первому и второму типу применимы различные формулы сокращенного умножения. Например, первое решается только посредством вынесения общего множителя за скобку, а для решения второго используется соотношение разности квадратов.

Однако не во всех случаях можно рассчитывать на формулы, поскольку большинство сложных заданий требуют выполнения математических преобразований.

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Формулы разложения на элементы

Для решения квадратного уравнения применяются соответствующие тождества, позволяющие понижать вторую степень. Запомнить их довольно просто, поскольку количество ограничено несколькими формулами разложения на множители (сокращенного умножения):

Первое и второе тождества называются квадратом суммы или разности соответственно. Их рекомендуется применять, когда уравнение невозможно разложить на множители. В этом случае следует выделить квадрат суммы или разности, а затем воспользоваться третьей формулой — разностью квадратов. Например, в тождестве 4t^2+4t-3=0 следует выделить квадрат суммы. Для этого нужно выполнить такие преобразования: (4t^2+4t+1)-1-3=(2t+1)^2-4=0. Последнее соотношение также возможно разложить на множители по формуле разности квадратов, т. е. (2t+1)^2-2^2=(2t+1-2)(2t+1+2)=(2t-1)(2t+3)=0.

В других случаях первое и второе соотношение использовать не рекомендуется, поскольку это может привести к увеличению времени и сложности вычислительных операций, что недопустимо для начинающих математиков. При этом количество ошибок возрастает и тратится время.

Разложить на множители квадратный трехчлен — значит представить его в виде отдельных выражений в скобках для оптимизации математических операций через упрощенные тождества.

Однако не всегда возможно воспользоваться вышеописанными тождествами. В этом случае пригодятся знания из алгебры, при помощи которых необходимо упростить выражение. Например, не всегда следует раскрывать скобки и приводить подобные элементы. Следует разобрать на примере уравнения такого вида: (5t-2)(2t+3)-(5t-2)(t-1)=0. Если раскрывать скобки и приводить общие элементы, то это займет некоторое время, т. е. (5t-2)(2t+3)-(5t-2)(t-1)=10t^2+15t-4t-6-5t^2+5t+2t-2=5t^2+4t-8=0. Последнее уравнение нужно решать через дискриминант, а это еще дополнительные расчеты и ценное время, которое может быть потрачено с пользой на другие задачи.

При решении равенства методом разложения на множители вычислительный процесс более оптимизирован, т. е. (5t-2)(2t+3)-(5t-2)(t-1)=(5t-2)(2t+3-t+1)=(5t-2)(t+4)=0. Чтобы решить последнее тождество, достаточно приравнять к нулю его множители, которые являются обыкновенными линейными уравнениями.

Видео:Разложение квадратного трехчлена на множители. Практическая часть. 1ч. 8 класс.Скачать

Корни уравнения

Перед использованием алгоритма необходимо разобрать, что означает решить уравнение. Если предположить, что существует некоторое тождество, состоящее из некоторых коэффициентов и переменных, то нужно посредством математических преобразований и формул вычислить значения неизвестных, при которых выражение принимает истинное значение. Например, 1=1 — истина.

Корни уравнения — допустимые значения переменных, если их подставить в исходное выражение, результат не изменяется. Следует отметить, что в некоторых случаях могут возникать ложные величины. Это очень часто происходит при решении кубических, биквадратных и других сложных выражений. Однако они могут возникать при решении квадратных двучленов.

Чтобы избавиться от ложных величин, необходимо выполнить единственное правило: подставить их в исходное тождество. Если решение получено графическим методом, то проверку можно не выполнять. Последний метод рекомендуется использовать также для проверки количества решений. Для этого достаточно схематичного построения графика функции, на котором и будут видны корни — точки пересечения с осями координат.

В алгебре можно также встретить задачи на эту тематику. Например, требуется найти точки пересечения двух или трех графических представлений. Однако у графического способа решения есть один существенный недостаток (при точном определении значений переменных) — только для целочисленных значений корней. Его рекомендуется использовать в различных онлайн-приложениях, позволяющих строить графики функций и точно определять точки пересечения.

Следует отметить, что для проверки правильности нахождения корней квадратного трехчлена или двучлена можно использовать также онлайн-калькуляторы, в поля которых вводятся коэффициенты при неизвестных и свободный член. После нажатия кнопки «вычислить» или «найти корни» программа мгновенно выдает результаты. Если какого-то члена в тождестве нет, то в соответствующем поле указывается нулевая величина.

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Алгоритм операции

Любое сложное действие рекомендуется выполнять по определенной методике, которая называется алгоритмом. При решении уравнений методом разложения на множители используется такая последовательность действий:

Написать уравнение.
Проанализировать возможность нахождения корней (выбор метода решения).
Упростить уравнение (разложить на множители по одной из формул сокращенного умножения).
Выполнить математические преобразования при необходимости.
Перенести 0 вправо, а все остальные части — влево.
Приравнять каждый из множителей к 0.
Найти корни для каждого элемента отдельно.
Отсеять ложные значения.
Записать окончательный результат.

Второй пункт алгоритма является очень важным, поскольку именно от него зависит правильность и скорость решения уравнения. Последнее должно раскладываться на множители. Вообще суть их решения сводится к их упрощению и приравниванию элементов в левой части к нулевому значению. В некоторых случаях требуется привести подобные слагаемые, а затем подвести результат к определенной формуле сокращенного умножения.

Следует отметить, что восьмой пункт методики — проверка. Однако ее специалисты рекомендуют новичкам выполнять на каждом этапе алгоритма, чтобы избежать ошибок при нахождении корней. Если учащиеся совершают много тренировок, то уже нет необходимости обращать внимание на пункты, поскольку постоянные тренировки делают вычислительный процесс автоматизированным.

Видео:Разложение квадратного трехчлена на множители.Скачать

Примеры решения

Для начала необходимо решить простое неполное квадратное уравнение t^2-4=0. Корни можно найти по вышеописанному алгоритму:

t^2-4=0.
Метод решения: разложение по формуле сокращенного умножения.
t^2-4=(t-2)(t+2)=0.
Выполнять математические преобразования нет необходимости.
(t-2)(t+2)=0.
(t-2)=0 и (t+2)=0.
t1=2 и t2=-2.
t^2-4=0: (-2)^2-4=4-4=0 (+) и 2^2-4=0 (+).
Решение: t1=-2 и t2=2 (значения записываются в порядке возрастания).

Следующее тождество является более сложным, т. е. 4t^2+28t+40=0. Решается оно посредством вычисления величины дискриминанта. Однако можно рассмотреть вариант понижения степени. Для этого требуется воспользоваться таким алгоритмом:

4t^2+28t+40=0.
Выделить полный квадрат: (4t^2+28t+49)-49+40=(2t+7)^2-9=0.
Разложить на сомножители: (2t+7-9)(2t+7+9)=(2t-2)(2t+16)=0.
Приравнять к 0: (2t-2)=0 или (2t+16)=0.
t1=2/2=1.
t2=-16/2=-8.
Подстановка t1 и t2: 4*1^2+28t+40=32+40=0 (-) и 4*(-8)^2+28t+40=40-40=0 (+).

При решении получено два корня, но это не означает, что при подстановке в исходное тождество они превращают его в истину. Следовательно, t1=1 — ложный корень, поскольку 72 не равно 0.

Таким образом, для решения квадратных уравнений подойдет метод разложения выражения с неизвестными на множители, поскольку эта операция позволит существенно оптимизировать процесс нахождения корней, избежать ошибок и сократить время вычислений.