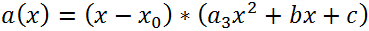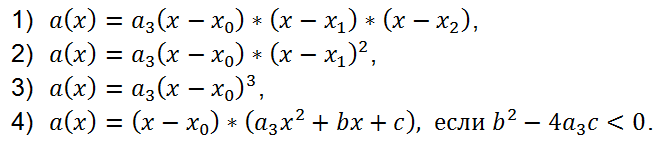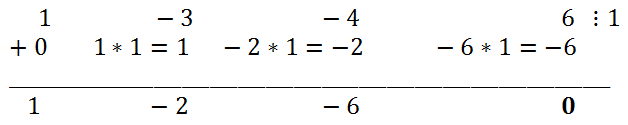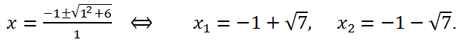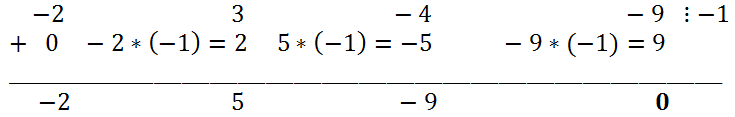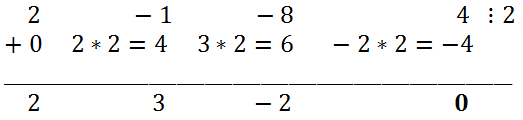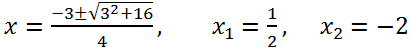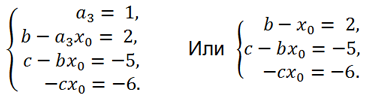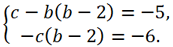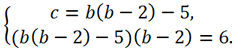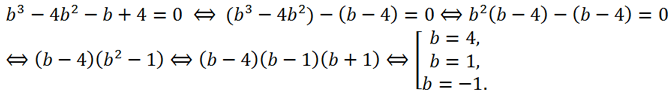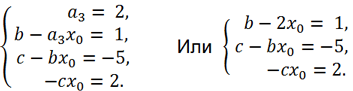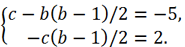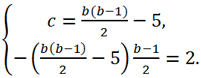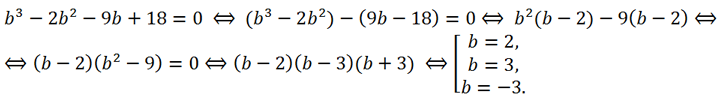Таким образом, кубический многочлен a(x) всегда можно разложить на два множителя, один из которых линейный, а второй квадратичный
В свою очередь многочлен второй степени a3x 2 + bx + c может иметь 2 различных действительных корня, 1 действительный корень или 2 комплексно сопряженных корня.
Соответственно, получаем такие случаи разложения на множители a(x):
Таким образом, приравнивая каждый множитель в разложении к нулю, найдем все корни кубического уравнения в каждом случае. Рассмотрим решение кубических уравнений методом разложения на множители на примерах.
Пример 1. Решить уравнение x 3 — 3x 2 — 4x + 6 = 0.
Делителями свободного члена являются числа: ±1, ±2, ±3, ±6. Значит, корни уравнения нужно искать среди них. Простой подстановкой убеждаемся, что корнем уравнения является число 1. Следовательно, исходное уравнение эквивалентно (x — 1)*(a3x 2 + bx + c) = 0.
Чтобы найти многочлен a3x 2 + bx + c, нужно левую часть исходного уравнения разделить на x — 1. Для деления многочлена на двучлен будем использовать схему Горнера.
Таким образом, x 3 — 3x 2 — 4x + 6 = (x — 1)(x 2 — 2x — 6). Следовательно, исходное уравнение эквивалентно (x — 1) (x 2 — 2x — 6) = 0.
Осталось решить квадратное уравнение x 2 — 2x — 6 = 0.
- Калькуляторы для решение примеров и задач по математике
- Решение кубических уравнений
- Решение двучленного кубического уравнения вида A x 3 + B = 0
- Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0
- Решение кубических уравнений с рациональными корнями
- Решение кубических уравнений по формуле Кардано
- Разложение на скобки кубического уравнения
- 📺 Видео
Видео:Математика | Кубические уравнения по методу СталлонеСкачать

Калькуляторы для решение примеров и задач по математике
Лучшие математические приложения для школьников и их родителей, студентов и учителей. Подробнее .
Пример 2. Решить уравнение -2x 3 + 3x 2 — 4x — 9 = 0.
Делителями свободного члена являются числа: ±1, ±3, ±9. Делителями старшего коэффициента являются числа: ±1, ±2.
Значит, корни исходного уравнения могут быть среди чисел: ±1, ±3, ±9,
Снова простой подстановкой убеждаемся, что -1 является корнем уравнения. С помощью схемы Горнера делим левую часть исходного уравнения на x + 1.
Таким образом, -2x 3 + 3x 2 — 4x — 9 = (x + 1)(-2x 2 + 5x — 9). Следовательно, исходное уравнение эквивалентно (x + 1) (-2x 2 + 5x — 9)=0. Решая квадратное уравнение -2x 2 + 5x — 9 = 0, получаем, что его дискриминант 3 — x 2 — 8x + 4 = 0.
Делителями свободного члена являются числа: ±1, ±2, ±4. Делителями старшего коэффициента являются числа: ±1, ±2.
Значит, корни исходного уравнения могут быть среди чисел: ±1, ±2, ±4.
Простой подстановкой убеждаемся, что 2 является корнем уравнения. С помощью схемы Горнера делим левую часть исходного уравнения на x — 2.
Таким образом, 2x 3 — x 2 — 8x + 4 = (x — 2)(2x 2 + 3x — 2). Следовательно, исходное уравнение эквивалентно (x — 2) (2x 2 + 3x — 2) = 0. Решая квадратное уравнение 2x 2 + 3x — 2 = 0, получаем,
Еще один способ разложения на множители многочлена третьей степени — метод неопределенных коэффициентов. Он довольно громоздкий, но иногда бывает очень полезным при решении разного рода задач, а не только в случае разложения на множители. Разложение на множители любого многочлена третьей степени можно представить следующим образом a(x) = (x-x0)*(a3x 2 + bx + c).
Раскрывая скобки, получим a(x) = a3x 3 + x 2 (b — a3x0) + x*(c — bx0) — cx0.
Приравнивая теперь коэффициенты при одинаковых степенях x и свободные члены в исходном многочлене и в многочлене a(x), получим систему из четырех уравнений и четырех неизвестных a3,b,c и x0. Рассмотрим применение метода неопределенных коэффициентов на примерах.
Пример 4. Решить уравнение x 3 + 2x 2 — 5x — 6 = 0.
Так как любой многочлен 3 степени можно представить в виде a3x 3 + x 2 (b — a3x0) + x*(c — bx0) — cx0, то приравнивая коэффициенты при одинаковых степенях x, получаем следующую систему уравнений:
Выразим из первого уравнения x0 = b — 2 и подставим в два оставшихся. Получим
Теперь выразим переменную c из первого уравнения и подставим во второе.
Раскрывая скобки во втором уравнении и решая его, находим b:
Если b=4, то c=3, x0 = 2. Следовательно, x 3 + 2x 2 — 5x — 6 = (x — 2)(x 2 — 4x + 3)=(x — 2)(x + 1)(x + 3).
Если b = 1, то c = -6, x0 = -1. Следовательно, x 3 + 2x 2 — 5x — 6 = (x + 1)(x 2 + x — 6)=(x + 1)(x + 3)(x — 2).
Если b = -1, то c = -2, x0 = -3. Следовательно, x 3 + 2x 2 — 5x — 6=(x + 3)(x 2 — x — 2) = (x + 3)(x — 2)(x + 1).
Таким образом, исходное уравнение эквивалентно уравнению (x + 3)(x — 2)(x + 1) = 0.
Приравнивая к нулю каждый из множителей, получаем корни уравнения x = -3, x = 2, x = -1.
Пример 5. Решить уравнение 2x 3 + x 2 — 5x + 2 = 0.
Приравнивая соответствующие коэффициенты при одинаковых степенях x, получаем следующую систему уравнений:
Выразим из первого уравнения x0 =
и подставим в два оставшихся. Получим
Теперь из первого уравнения выразим переменную c и подставим во второе.
Умножая левую и правую части второго уравнения на 4 и раскрывая скобки, находим b:
Если b = 3, то c = -2, x0 = 1. Следовательно, 2x 3 + x 2 — 5x + 2 = (x — 1)(2x 2 + 3x — 2)=2(x — 1)(x —
Если b = -3, то c = 1, x0 = -2. Следовательно, 2x 3 + x 2 — 5x + 2 = (x + 2)(2x 2 — 3x + 1) = 2(x + 2)(x —
Следовательно, исходное уравнение эквивалентно уравнению 2(x + 2)(x —
Приравнивая к нулю каждый из множителей, получаем корни уравнения x = -2, x =
Видео:Теорема Безу и разложение многочлена на множителиСкачать

Решение кубических уравнений
Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.
Видео:Разложение кубических выражений на множителиСкачать

Решение двучленного кубического уравнения вида A x 3 + B = 0
Кубическое уравнение, содержащее двучлен, имеет вид A x 3 + B = 0 . Его необходимо приводить к x 3 + B A = 0 с помощью деления на А , отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что
x 3 + B A = 0 x + B A 3 x 2 — B A 3 x + B A 2 3 = 0
Результат первой скобки примет вид x = — B A 3 , а квадратный трехчлен — x 2 — B A 3 x + B A 2 3 , причем только с комплексными корнями.
Найти корни кубического уравнения 2 x 3 — 3 = 0 .
Решение
Необходимо найти х из уравнения. Запишем:
2 x 3 — 3 = 0 x 3 — 3 2 = 0
Необходимо применить формулу сокращенного умножения. Тогда получим, что
x 3 — 3 2 = 0 x — 3 3 2 6 x 2 + 3 3 2 6 x + 9 2 3 = 0
Раскроем первую скобку и получим x = 3 3 2 6 . Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.
Ответ: x = 3 3 2 6 .
Видео:Произведение многочленов. Разложение многочлена на множители способом группировки. 7 класс.Скачать

Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0
Вид квадратного уравнения — A x 3 + B x 2 + B x + A = 0 , где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что
A x 3 + B x 2 + B x + A = A x 3 + 1 + B x 2 + x = = A x + 1 x 2 — x + 1 + B x x + 1 = x + 1 A x 2 + x B — A + A
Корень уравнения равен х = — 1 , тогда для получения корней квадратного трехчлена A x 2 + x B — A + A необходимо задействовать через нахождение дискриминанта.
Решить уравнение вида 5 x 3 — 8 x 2 — 8 x + 5 = 0 .
Решение
Уравнение является возвратным. Необходимо произвести группировку. Получим, что
5 x 3 — 8 x 2 — 8 x + 5 = 5 x 3 + 1 — 8 x 2 + x = = 5 x + 1 x 2 — x + 1 — 8 x x + 1 = x + 1 5 x 2 — 5 x + 5 — 8 x = = x + 1 5 x 2 — 13 x + 5 = 0
Если х = — 1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5 x 2 — 13 x + 5 :
5 x 2 — 13 x + 5 = 0 D = ( — 13 ) 2 — 4 · 5 · 5 = 69 x 1 = 13 + 69 2 · 5 = 13 10 + 69 10 x 2 = 13 — 69 2 · 5 = 13 10 — 69 10
Ответ:
x 1 = 13 10 + 69 10 x 2 = 13 10 — 69 10 x 3 = — 1
Видео:Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Решение кубических уравнений с рациональными корнями
Если х = 0 , то он является корнем уравнения вида A x 3 + B x 2 + C x + D = 0 . При свободном члене D = 0 уравнение принимает вид A x 3 + B x 2 + C x = 0 . При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид x A x 2 + B x + C = 0 .
Найти корни заданного уравнения 3 x 3 + 4 x 2 + 2 x = 0 .
Решение
3 x 3 + 4 x 2 + 2 x = 0 x 3 x 2 + 4 x + 2 = 0
Х = 0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3 x 2 + 4 x + 2 . Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что
D = 4 2 — 4 · 3 · 2 = — 8 . Так как его значение отрицательное, то корней трехчлена нет.
Ответ: х = 0 .
Когда коэффициенты уравнения A x 3 + B x 2 + C x + D = 0 целые, то в ответе можно получить иррациональные корни. Если A ≠ 1 , тогда при умножении на A 2 обеих частей уравнения проводится замена переменных, то есть у = А х :
A x 3 + B x 2 + C x + D = 0 A 3 · x 3 + B · A 2 · x 2 + C · A · A · x + D · A 2 = 0 y = A · x ⇒ y 3 + B · y 2 + C · A · y + D · A 2
Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными. Чтобы получить тождественное равенство, необходимо произвести подстановку делителей в полученное уравнение. Тогда полученный y 1 будет являться корнем. Значит и корнем исходного уравнения вида x 1 = y 1 A . Необходимо произвести деление многочлена A x 3 + B x 2 + C x + D на x — x 1 . Тогда сможем найти корни квадратного трехчлена.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Необходимо произвести преобразование с помощью умножения на 2 2 обеих частей, причем с заменой переменной типа у = 2 х . Получаем, что
2 x 3 — 11 x 2 + 12 x + 9 = 0 2 3 x 3 — 11 · 2 2 x 2 + 24 · 2 x + 36 = 0 y = 2 x ⇒ y 3 — 11 y 2 + 24 y + 36 = 0
Свободный член равняется 36 , тогда необходимо зафиксировать все его делители:
± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 9 , ± 12 , ± 36
Необходимо произвести подстановку y 3 — 11 y 2 + 24 y + 36 = 0 , чтобы получить тождество вида
1 3 — 11 · 1 2 + 24 · 1 + 36 = 50 ≠ 0 ( — 1 ) 3 — 11 · ( — 1 ) 2 + 24 · ( — 1 ) + 36 = 0
Отсюда видим, что у = — 1 – это корень. Значит, x = y 2 = — 1 2 .
Далее следует деление 2 x 3 — 11 x 2 + 12 x + 9 на x + 1 2 при помощи схемы Горнера:
| x i | Коэффициенты многочлена | |||
|---|---|---|---|---|
| 2 | — 11 | 12 | 9 | |
| — 0 . 5 | 2 | — 11 + 2 · ( — 0 . 5 ) = — 12 | 12 — 12 · ( — 0 . 5 ) = 18 | 9 + 18 · ( — 0 . 5 ) = 0 |
2 x 3 — 11 x 2 + 12 x + 9 = x + 1 2 2 x 2 — 12 x + 18 = = 2 x + 1 2 x 2 — 6 x + 9
После чего необходимо найти корни квадратного уравнения вида x 2 — 6 x + 9 . Имеем, что уравнение следует привести к виду x 2 — 6 x + 9 = x — 3 2 , где х = 3 будет его корнем.
Ответ: x 1 = — 1 2 , x 2 , 3 = 3 .
Алгоритм можно применять для возвратных уравнений. Видно, что — 1 – это его корень, значит, левая часть может быть поделена на х + 1 . Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.
Видео:Разложение квадратного трехчлена на множители. 8 класс.Скачать

Решение кубических уравнений по формуле Кардано
Нахождение кубических корней возможно при помощи формулы Кардано. При A 0 x 3 + A 1 x 2 + A 2 x + A 3 = 0 необходимо найти B 1 = A 1 A 0 , B 2 = A 2 A 0 , B 3 = A 3 A 0 .
После чего p = — B 1 2 3 + B 2 и q = 2 B 1 3 27 — B 1 B 2 3 + B 3 .
Полученные p и q в формулу Кардано. Получим, что
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3
Подбор кубических корней должен удовлетворять на выходе значению — p 3 . Тогда корни исходного уравнения x = y — B 1 3 . Рассмотрим решение предыдущего примера, используя формулу Кардано.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Видно, что A 0 = 2 , A 1 = — 11 , A 2 = 12 , A 3 = 9 .
Необходимо найти B 1 = A 1 A 0 = — 11 2 , B 2 = A 2 A 0 = 12 2 = 6 , B 3 = A 3 A 0 = 9 2 .
Отсюда следует, что
p = — B 1 2 3 + B 2 = — — 11 2 2 3 + 6 = — 121 12 + 6 = — 49 12 q = 2 B 1 3 27 — B 1 B 2 3 + B 3 = 2 · — 11 2 3 27 — — 11 2 · 6 3 + 9 2 = 343 108
Производим подстановку в формулу Кордано и получим
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — — q 2 4 + p 3 27 3 = = — 343 216 + 343 2 4 · 108 2 — 49 3 27 · 12 3 3 + — 343 216 — 343 2 4 · 108 2 — 49 3 27 · 12 3 3 = = — 343 216 3 + — 343 216 3
— 343 216 3 имеет три значения. Рассмотрим их ниже.
— 343 216 3 = 7 6 cos π + 2 π · k 3 + i · sin π + 2 π · k 3 , k = 0 , 1 , 2
Если k = 0 , тогда — 343 216 3 = 7 6 cos π 3 + i · sin π 3 = 7 6 1 2 + i · 3 2
Если k = 1 , тогда — 343 216 3 = 7 6 cosπ + i · sinπ = — 7 6
Если k = 2 , тогда — 343 216 3 = 7 6 cos 5 π 3 + i · sin 5 π 3 = 7 6 1 2 — i · 3 2
Необходимо произвести разбиение по парам, тогда получим — p 3 = 49 36 .
Тогда получим пары: 7 6 1 2 + i · 3 2 и 7 6 1 2 — i · 3 2 , — 7 6 и — 7 6 , 7 6 1 2 — i · 3 2 и 7 6 1 2 + i · 3 2 .
Преобразуем при помощи формулы Кордано:
y 1 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 + i · 3 2 + 7 6 1 2 — i · 3 2 = 7 6 1 4 + 3 4 = 7 6 y 2 = — 343 216 3 + — 343 216 3 = — 7 6 + — 7 6 = — 14 6 y 3 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 — i · 3 2 + 7 6 1 2 + i · 3 2 = 7 6 1 4 + 3 4 = 7 6
x 1 = y 1 — B 1 3 = 7 6 + 11 6 = 3 x 2 = y 2 — B 1 3 = — 14 6 + 11 6 = — 1 2 x 3 = y 3 — B 1 3 = 7 6 + 11 6 = 3
Ответ: x 1 = — 1 2 , x 2 , 3 = 3
При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.
Видео:Математика - Разложение трехчлена на множителиСкачать

Разложение на скобки кубического уравнения
Нам уже известны формулы для решения квадратных уравнений. А что делать, если встретится уравнение более высокой степени ? Оказы вается, что для уравнений третьей и четвёртой степени есть формулы, позволяющие найти корни (но они редко используются на практике ввиду их громоздкости), а для уравнений пятой степени и выше доказано, что таких формул не существует. Таким образом, у нас не выйдет в общем случае решить уравнение третьей или более высокой степени. Но существует ряд приёмов, позволяющих решить некоторые специальные виды уравнений. К их рассмотрению мы сейчас и перейдём.
Решите уравнение: `x^3 +4x^2 — 2x-3=0`.
Заметим, что `x=1` является корнем уравнения (значение многочлена при `x=1` равно сумме коэффициентов многочлена). Тогда по теореме Безу многочлен `x^3 +4x^2 -2x -3` делится на многочлен `x-1`. Выполнив деление, получаем:
`x^3 +4x^2 -2x -3=0 hArr (x-1)(x^2 + 5x +3) =0 hArr`
Обычно кубические уравнения решают именно так: подбирают один корень, выполняют деление уголком, после чего остаётся решить только квадратное уравнение. А что делать, если у нас уравнение четвёртой степени? Тогда придётся подбирать корень два раза. После подбора первого корня и деления останется кубическое уравнение, у которого надо будет подобрать ещё один корень. Возникает вопрос. Что делать, если такие «простые» числа как `+-1`, `+-2` не являются корнями уравне ния? Неужели тогда надо перебирать всевозможные числа? Ответ на этот вопрос даёт следующее утверждение.
Если несократимая дробь `p//q` (`p` — целое, `q` — натуральное) является корнем многочлена с целыми коэффициентами , то сво бодный член делится на `p` , а старший коэффициент делится на `q`.
Пусть несократимая дробь `p//q` — корень многочлена (8). Это означает, что
`a_n (p/q)^n +a_(n-1)(p/q)^(n-1) + a_(n-2) (p/q)^(n-2)+ . «+a_2 (p/q)^2 +a_1(p/q)+0=0`.
Умножим обе части на `q^n`, получаем:
`a_n p^n + a_(n-1) p^(n-1) q+a_(n-2) p^(n-2) q^2 + . + a_2 p^2 q^(n-2) +a_1 pq^(n-1)+a_0q^n=0`.
Перенесём в правую часть, а из оставшихся слагаемых вынесем `p` за скобки:
Справа и слева в (14) записаны целые числа. Левая часть делится на `p=>` правая часть также делится на `p`. Числа `p` и `q` взаимно просты (т. к. дробь `p//q` несократимая), откуда следует, что `a_0 vdotsp`.
Аналогично доказывается, что `a_n vdotsq`. Теорема доказана.
Как правило, предлагаемые вам уравнения имеют целые корни, поэтому в большинстве задач используется следующее: если у многочлена с целыми коэффициентами есть целые корни, то они являются делителями свободного члена.
а) `x^4+4x^3-102x^2-644x-539=0`; (15)
б) `6x^4-35x^3+28x^2+51x+10=0`. (16)
а) Попробуем найти целые корни уравнения. Пусть `p` — корень. Тогда `539vdotsp`; чтобы найти возможные значения `p`, разложим число `539` на простые множители:
Поэтому `p` может принимать значения:
Подстановкой убеждаемся, что `x=-1` является корнем уравнения. Разделим многочлен в левой части (15) уголком на `x+1` и получим:
Далее подбираем корни у получившегося многочлена третьей степени. Получаем `x=-7`, а после деления на `(x+7)` остаётся `(x+1)(x+7)(x^2-4x-77)=0`. Решая квадратное уравнение, находим окончательное разложение левой части на множители:
1) После того, как найден первый корень, лучше сначала выполнить деление уголком, и только потом приступать к поиску последующих корней. Тогда вычислений будет меньше.
2) В разложении многочлена на множители множитель `(x+7)` встретился дважды. Тогда говорят, что `(–7)` является корнем кратности два. Аналогично говорят о корнях кратности три, четыре и т. д.
б) Если уравнение имеет рациональный корень `x_0=p/q`, то `10vdotsp`, `6vdotsq`, т. е. `p in`; `qin`.Возможные варианты для `x_0`:
Начинаем перебирать числа из этого списка. Первым подходит число `x=5/2`. Делим многочлен в левой части (16) на `(2x-5)` и получаем
Заметим, что для получившегося кубического уравнения выбор рациональных корней заметно сузился, а именно, следующие числа могут быть корнями: `x_0=+-1,+-2,+-1/3,+-2/3`, причём мы уже знаем, что числа `+-1` и `+-2` корнями не являются (так как мы их подставляли раньше, и они не подошли). Находим, что `x=-2/3` — корень; делим `3x^3-10x^2-11x-2` на `3x+2` и получаем:
Решаем квадратное уравнение: `x^2-4x-1=0 iff x=2+-sqrt5`.
К сожалению, уравнения не всегда имеют рациональные корни. Тогда приходится прибегать к другим методам.
Разложите на множители:
а) `x^4+4=x^4+4x^2+4-4x^2=(x^2+2)^2-(2x)^2=`
Таким образом, сумму четвёртых степеней, в отличие от суммы квадратов, можно разложить на множители:
в) Вынесем `x^2` за скобки и сгруппируем:
Обозначим `x+2/x=t`. Тогда `x^2+4+4/x^2=t^2`, `x^2+4/x^2=t^2-4`, выражение в скобках принимает вид:
В итоге получаем:
Этот приём иногда используется для решения уравнений четвёртой степени; в частности, с его помощью решают возвратные уравнения (см. пример 12 е).
г)* Можно убедиться, что никакой из рассмотренных выше методов не помогает решить задачу, а именно: рациональных корней уравнение не имеет (числа `+-1` и `+-2` – не корни); вынесение числа `x^2` за скобки и группировка слагаемых приводит к выражению
Если здесь обозначить `4x-13/x=t`, то `x^2-2/x^2` через `t` рационально не выражается.
Прибегнем к методу неопределённых коэффициентов. Пусть
Попробуем подобрать коэффициенты `a`, `b`, `c`, `d` так, чтобы (17) обратилось в верное равенство. Для этого раскроем скобки в правой части и приведём подобные слагаемые:
Приравняем в (18) коэффициенты при одинаковых степенях в обеих частях уравнения. Получим систему уравнений:
Мы будем пытаться найти целочисленные решения системы (19). Найти все решения системы (19) не проще, чем решить исходную задачу, однако нахождение целочисленных решений – разумеется, если они есть – нам по силам.
Рассмотрим четвёртое уравнение. Возможны только два принципиально различных случая:
2) `b=2` и `d=-1`. Рассмотрим каждый из них. Подставляем значения `b` и `d` в первые три уравнения:
Из первого и третьего уравнений системы получаем `c=5/3`; `a=-17/3`, что не удовлетворяет второму уравнению, поэтому система решений не имеет; пара чисел `b=1` и `d=-2` не подходит.
Эта система имеет одно решение `a=-7`, `c=3`. Значит, числа `a=-7`, `b=2`, `c=3`, `d=-1` являются решением системы (19), поэтому
Далее каждый из квадратных трёхчленов можно разложить на множители.
Во многих ситуациях степень уравнения можно понизить с помощью замены переменных.
📺 Видео
КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Математика| Разложение квадратного трехчлена на множители.Скачать

Схема Горнера. 10 класс.Скачать

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Как решать кубические уравнения Решите уравнение 3 степени 9 класс Разложить на множители ДелениеСкачать

РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ / Алгебра 7 классСкачать

Разложение на множители. 7 класс. Вебинар | МатематикаСкачать

Алгебра 10 класс (Урок№12 - Решение алгебраических уравнений разложением на множители.)Скачать

ОГЭ. Задание 21. Уравнение третей степени. Разложение на множители.Скачать

Разложение многочлена на множители способом группировки. Алгебра, 7 классСкачать

ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать

7 класс, 29 урок, Способ группировкиСкачать

Решение уравнений с помощью разложения на множители | Алгебра 7 класс #23 | ИнфоурокСкачать